Development and Thermophysical Profile of Cetyl Alcohol-in-Water Nanoemulsions for Thermal Management †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Nanoemulsion Formulation and Preparation
2.3. Thermophysical Profile
3. Results
3.1. Optimization of Emulsion Composition and Stability
3.2. Phase Change Chracteristics
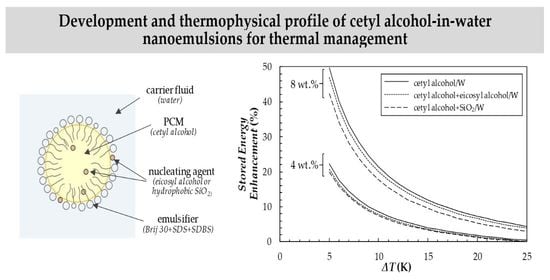
3.3. Heat Storage Capacity
3.4. Dynamic Viscosities
3.5. Thermal Conductivity
3.6. Density
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
Nomenclature
| AAD% | percentage absolute average deviations; |
| Ai | second-order polynomial coefficients |
| αp | thermal expansivity [K−1]; |
| β | heating/cooling scanning rate [K·min−1] |
| cp | isobaric heat capacity [J·g−1·g−1] |
| C16OH | cetyl alcohol or 1-hexadecanol |
| C20OH | eicosyl alcohol or 1-eicosanol |
| CTAC | cetyltrimethylammonium chloride |
| DLS | dynamic light scattering |
| DSC | differential scanning calorimetry |
| Δhlatent | latent heat [J·g−1] |
| ΔT | temperature difference covered by the sample [K] |
| φ | volume fraction; |
| shear rate [s−1]; | |
| NA | nucleating agent |
| N2 | nitrogen |
| HAVC | heating, ventilation and air conditioning |
| PBS | phosphate buffer solution |
| PCM | phase change material |
| PCME | phase change material emulsion |
| pdi | polydispersity index |
| ρ | density [g·cm−3] |
| s | standard deviation |
| SDBS | sodium dodecylbenzenesulfonate |
| SDS | sodium dodecyl sulfate |
| SFT | surfactant |
| SiO2 | silica nanoparticles |
| T | temperature [K] |
| TES | thermal energy storage |
| λ | thermal conductivity [W·m−1·K−1] |
| μ | shear dynamic viscosity [mPa·s] |
| μr = μPCM/μwater+SDS | relative viscosity of sample to corresponding water + SDS mixture |
| VFT | Vogel-Fulcher-Tamman-Hesse (μ0, D and T0: VFT fitting coefficients) |
| W | water; |
| wt.% | mass concentration |
| Subscripts | |
| CF | carrier fluid |
| latent | latent |
| melt. | melting |
| p | peak temperature |
| PCM | phase change materials |
| PCME | phase change material emulsion |
| sol. | solidification. |
References
- Bretschger, L.; Pittel, K. Twenty key challenges in environmental and resource economics. Environ. Resour. Econ. 2020, 77, 725–750. [Google Scholar] [CrossRef]
- Colmenar-Santos, A.; Muñoz-Gómez, A.-M.; López-Rey, Á.; Rosales-Asensio, E. Strategy to support renewable energy sources in Europe. In Design, Analysis, and Applications of Renewable Energy Systems. Advances in Nonlinear Dynamics and Chaos (ANDC); Academic Press: Cambridge, MA, USA, 2021; pp. 103–120. [Google Scholar] [CrossRef]
- Nieto, J.; Carpintero, Ó.; Lobejón, L.F.; Miguel, L.J. An ecological macroeconomics model: The energy transition in the EU. Energy Policy 2020, 145, 111726. [Google Scholar] [CrossRef]
- Saha, S.; Ruslan, A.R.M.; Monjur Morshed, A.K.M.; Hasanuzzaman, M. Global prospects and challenges of latent heat thermal energy storage: A review. Clean Technol. Environ. Policy 2021, 23, 531–559. [Google Scholar] [CrossRef]
- Zhang, H.; Baeyens, J.; Cáceres, G.; Degrève, J.; Lv, Y. Thermal energy storage: Recent developments and practical aspects. Prog. Energy Combust. Sci. 2016, 53, 1–40. [Google Scholar] [CrossRef]
- Pielichowska, K.; Pielichowski, K. Phase change materials for thermal energy storage. Prog. Mater. Sci. 2014, 65, 67–123. [Google Scholar] [CrossRef]
- O’Neill, P.; Fischer, L.; Revellin, R.; Bonjour, J. Phase change dispersions: A literature review on their thermo-rheological performance for cooling applications. Appl. Therm. Eng. 2021, 192, 116920. [Google Scholar] [CrossRef]
- Cabaleiro, D.; Hamze, S.; Agresti, F.; Estellé, P.; Barison, S.; Fedele, L.; Bobbo, S. Dynamic viscosity, surface tension and wetting behavior studies of paraffin–in–water nano–emulsions. Energies 2019, 12, 3334. [Google Scholar] [CrossRef] [Green Version]
- Morimoto, T.; Suzuki, K.; Kumano, H. Heat transfer characteristics of phase change emulsions with solidification of phase change material particles in a circular tube. Int. J. Refrig. 2020, 114, 1–9. [Google Scholar] [CrossRef]
- Mikkola, V.; Puupponen, S.; Saari, K.; Ala-Nissila, T.; Seppälä, A. Thermal properties and convective heat transfer of phase changing paraffin nanofluids. Int. J. Therm. Sci. 2017, 117, 163–171. [Google Scholar] [CrossRef] [Green Version]
- Morimoto, T.; Kawana, Y.; Saegusa, K.; Kumano, H. Supercooling characteristics of phase change material particles within phase change emulsions. Int. J. Refrig. 2019, 99, 1–7. [Google Scholar] [CrossRef]
- Schalbart, P.; Kawaji, M. Comparison of paraffin nanoemulsions prepared by low-energy emulsification method for latent heat storage. Int. J. Therm. Sci. 2013, 67, 113–119. [Google Scholar] [CrossRef]
- Puupponen, S.; Seppälä, A.; Vartia, O.; Saari, K.; Ala-Nissilä, T. Preparation of paraffin and fatty acid phase changing nanoemulsions for heat transfer. Thermochim. Acta 2015, 601, 33–38. [Google Scholar] [CrossRef]
- Delgado-Sánchez, C.; Cuadri, A.A.; Navarro, F.J.; Partal, P. Formulation and processing of novel non-aqueous polyethylene glycol-in-silicone oil (o/o) phase change emulsions. Sol. Energy Mater. Sol. Cells 2021, 221, 110898. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, N.; Tao, W.; Cao, X.; He, Y. Fatty acids as phase change materials: A review. Renew. Sustain. Energy Rev. 2014, 29, 482–498. [Google Scholar] [CrossRef]
- Ghadim, H.B.; Shahbaz, K.; Al-Shannaq, R.; Farid, M.M. Binary mixtures of fatty alcohols and fatty acid esters as novel solid-liquid phase change materials. Int. J. Energy Res. 2019, 43, 8536–8547. [Google Scholar] [CrossRef]
- Zhang, Z.; Yuan, Y.; Zhang, N.; Cao, X. Thermophysical properties of some fatty acids/surfactants as phase change slurries for thermal energy storage. J. Chem. Eng. Data 2015, 60, 2495–2501. [Google Scholar] [CrossRef]
- Fischer, L.; Mura, E.; O’Neill, P.; von Arx, S.; Worlitschek, J.; Qiao, G.; Li, Q.; Ding, Y. Thermophysical properties of a phase change dispersion for cooling around 50 °C. Int. J. Refrig. 2020, 119, 410–419. [Google Scholar] [CrossRef]
- Fischer, L.; Mura, E.; O’Neill, P.; Von Arx, S.; Worlitschek, J.; Qiao, G.; Li, Q.; Ding, Y. Heat transfer performance potential with a high-temperature phase change dispersion. Energies 2021, 14, 4899. [Google Scholar] [CrossRef]
- Li, Q.; Qiao, G.; Mura, E.; Li, C.; Fischer, L.; Ding, Y. Experimental and numerical studies of a fatty acid based phase change dispersion for enhancing cooling of high voltage electrical devices. Energy 2020, 198, 117280. [Google Scholar] [CrossRef]
- Yin, D.; Ma, L.; Geng, W.; Zhang, B.; Zhang, Q. Microencapsulation of n-hexadecanol by in situ polymerization of melamine–formaldehyde resin in emulsion stabilized by styrene–maleic anhydride copolymer. Arch. Thermodyn. 2015, 39, 661–667. [Google Scholar] [CrossRef]
- Shang, Y.; Zhang, D. Preparation and thermal properties of graphene oxide–microencapsulated phase change materials. Nanoscale Microscale Thermophys. Eng. 2016, 20, 147–157. [Google Scholar] [CrossRef]
- Wu, B.; Shi, L.; Zhang, Q.; Wang, W.J. Microencapsulation of 1-hexadecanol as a phase change material with reversible thermochromic properties. RSC Adv. 2017, 7, 42129–42137. [Google Scholar] [CrossRef] [Green Version]
- Feczkó, T.; Trif, L.; Horák, D. Latent heat storage by silica-coated polymer beads containing organic phase change materials. Sol. Energy 2016, 132, 405–414. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Li, X.; Shen, C.; Mao, Z.; Xu, H.; Zhong, Y.; Sui, X.; Feng, X.; Wang, B. Lignin assisted Pickering emulsion polymerization to microencapsulate 1-tetradecanol for thermal management. Int. J. Biol. Macromol. 2020, 146, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Jiang, M.; Li, Q.; Li, D.; Huang, J.; Hu, W.; Dong, L.; Xie, H.; Xiong1, C. Facile preparation and thermal performances of hexadecanol/crosslinked polystyrene core/shell nanocapsules as phase change material. Polym. Compos. 2014, 35, 2154–2158. [Google Scholar] [CrossRef]
- Zhang, X.; Niu, J.; Wu, J. yong Evaluation and manipulation of the key emulsification factors toward highly stable PCM-water nano-emulsions for thermal energy storage. Sol. Energy Mater. Sol. Cells 2021, 219, 110820. [Google Scholar] [CrossRef]
- McClements, D.J. Nanoemulsions versus microemulsions: Terminology, differences, and similarities. Soft Matter 2012, 8, 1719–1729. [Google Scholar] [CrossRef]
- Huang, L.; Doetsch, C.; Pollerberg, C. Low temperature paraffin phase change emulsions. Int. J. Refrig. 2010, 33, 1583–1589. [Google Scholar] [CrossRef]
- Shao, J.; Darkwa, J.; Kokogiannakis, G. Development of a novel phase change material emulsion for cooling systems. Renew. Energy 2016, 87, 509–516. [Google Scholar] [CrossRef] [Green Version]
- Safari, A.; Saidur, R.; Sulaiman, F.A.; Xu, Y.; Dong, J. A review on supercooling of phase change materials in thermal energy storage systems. Renew. Sustain. Energy Rev. 2017, 70, 905–919. [Google Scholar] [CrossRef]
- Huang, L.; Günther, E.; Doetsch, C.; Mehling, H. Subcooling in PCM emulsions-Part 1: Experimental. Thermochim. Acta 2010, 509, 93–99. [Google Scholar] [CrossRef]
- Cabaleiro, D.; Agresti, F.; Barison, S.; Marcos, M.A.; Prado, J.I.; Rossi, S.; Bobbo, S.; Fedele, L. Development of paraffinic phase change material nanoemulsions for thermal energy storage and transport in low-temperature applications. Appl. Therm. Eng. 2019, 159, 113868. [Google Scholar] [CrossRef]
- Agresti, F.; Fedele, L.; Rossi, S.; Cabaleiro, D.; Bobbo, S.; Ischia, G.; Barison, S. Nano-encapsulated PCM emulsions prepared by a solvent-assisted method for solar applications. Sol. Energy Mater. Sol. Cells 2019, 194, 268–275. [Google Scholar] [CrossRef]
- Barison, S.; Cabaleiro, D.; Rossi, S.; Kovtun, A.; Melucci, M.; Agresti, F. Paraffin–graphene oxide hybrid nano emulsions for thermal management systems. Colloids Surf. A Physicochem. Eng. Asp. 2021, 627, 127132. [Google Scholar] [CrossRef]
- Wang, F.; Liu, J.; Fang, X.; Zhang, Z. Graphite nanoparticles-dispersed paraffin/water emulsion with enhanced thermal-physical property and photo-thermal performance. Sol. Energy Mater. Sol. Cells 2016, 147, 101–107. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, C.; Liu, J.; Fang, X.; Zhang, Z. Highly stable graphite nanoparticle-dispersed phase change emulsions with little supercooling and high thermal conductivity for cold energy storage. Appl. Energy 2017, 188, 97–106. [Google Scholar] [CrossRef]
- Zhang, X.; Niu, J.; Zhang, S.; Wu, J.Y. PCM in water emulsions: Supercooling reduction effects of nano-additives, viscosity effects of surfactants and stability. Adv. Eng. Mater. 2015, 17, 181–188. [Google Scholar] [CrossRef]
- Zhang, X.; Niu, J.; Wu, J.Y. Development and characterization of novel and stable silicon nanoparticles-embedded PCM-in-water emulsions for thermal energy storage. Appl. Energy 2019, 238, 1407–1416. [Google Scholar] [CrossRef]
- Zhang, G.; Yu, Z.; Cui, G.; Dou, B.; Lu, W.; Yan, X. Fabrication of a novel nano phase change material emulsion with low supercooling and enhanced thermal conductivity. Renew. Energy 2020, 151, 542–550. [Google Scholar] [CrossRef]
- Fischer, L.J.; von Arx, S.; Wechsler, U.; Züst, S.; Worlitschek, J. Phase change dispersion properties, modeling apparent heat capacity. Int. J. Refrig. 2017, 74, 240–253. [Google Scholar] [CrossRef]
- Fischer, L.J.; Von Arx, S.; Wechsler, U.; Züst, S.; Worlitschek, J. Phase change dispersion, potentially a new class of heat transfer fluids. J. Phys. Conf. Ser. 2016, 745, 032133. [Google Scholar] [CrossRef] [Green Version]
- Huang, L.; Noeres, P.; Petermann, M.; Doetsch, C. Experimental study on heat capacity of paraffin/water phase change emulsion. Energy Convers. Manag. 2010, 51, 1264–1269. [Google Scholar] [CrossRef]
- Liu, L.; Niu, J.; Wu, J.Y. Formulation of highly stable PCM nano-emulsions with reduced supercooling for thermal energy storage using surfactant mixtures. Sol. Energy Mater. Sol. Cells 2021, 223, 110983. [Google Scholar] [CrossRef]
- Lu, W.; Tassou, S.A. Experimental study of the thermal characteristics of phase change slurries for active cooling. Appl. Energy 2012, 91, 366–374. [Google Scholar] [CrossRef]
- Huang, L.; Petermann, M.; Doetsch, C. Evaluation of paraffin/water emulsion as a phase change slurry for cooling applications. Energy 2009, 34, 1145–1155. [Google Scholar] [CrossRef]
- Günther, E.; Huang, L.; Mehling, H.; Dötsch, C. Subcooling in PCM emulsions-Part 2: Interpretation in terms of nucleation theory. Thermochim. Acta 2011, 522, 199–204. [Google Scholar] [CrossRef]
- Zhao, Q.; Yang, W.; Zhang, H.; He, F.; Yan, H.; He, R.; Zhang, K.; Fan, J. Graphene oxide Pickering phase change material emulsions with high thermal conductivity and photo-thermal performance for thermal energy management. Colloids Surf. A Physicochem. Eng. Asp. 2019, 575, 42–49. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, J.Y.; Niu, J. PCM-in-water emulsion for solar thermal applications: The effects of emulsifiers and emulsification conditions on thermal performance, stability and rheology characteristics. Sol. Energy Mater. Sol. Cells 2016, 147, 211–224. [Google Scholar] [CrossRef]
- Wang, F.; Lin, W.; Ling, Z.; Fang, X. A comprehensive review on phase change material emulsions: Fabrication, characteristics, and heat transfer performance. Sol. Energy Mater. Sol. Cells 2019, 191, 218–234. [Google Scholar] [CrossRef]
- Shao, J.; Darkwa, J.; Kokogiannakis, G. Review of phase change emulsions (PCMEs) and their applications in HVAC systems. Energy Build. 2015, 94, 200–217. [Google Scholar] [CrossRef] [Green Version]
- Rinaldi, G.; Lazaro, A.; Delgado, M.; Marin, J.M.; Peñalosa, C.; Lozano, M.A.; Serra, L.M.; Verda, V. Study on seasonal and short-term thermal energy storage using a phase change material emulsion for district heating applications. In Proceedings of the ISES Solar World Conference 2017 and the IEA SHC Solar Heating and Cooling Conference for Buildings and Industry, Abu Dhabi, United Arab Emirates, 29 October–2 November 2017; pp. 771–782. [Google Scholar] [CrossRef]
- Cao, J.; He, Y.; Feng, J.; Lin, S.; Ling, Z.; Zhang, Z.; Fang, X. Mini-channel cold plate with nano phase change material emulsion for Li-ion battery under high-rate discharge. Appl. Energy 2020, 279, 115808. [Google Scholar] [CrossRef]
- Fedele, L.; Colla, L.; Bobbo, S.; Barison, S.; Agresti, F. Experimental stability analysis of different water- based nanofluids. Nanoscale Res. Lett. 2011, 6, 300. [Google Scholar] [CrossRef] [Green Version]
- Hassan, P.A.; Rana, S.; Verma, G. Making sense of Brownian motion: Colloid characterization by dynamic light scattering. Langmuir 2015, 31, 3–12. [Google Scholar] [CrossRef]
- Cabaleiro, D.; Gracia-Fernández, C.; Lugo, L. (Solid + liquid) phase equilibria and heat capacity of (diphenyl ether + biphenyl) mixtures used as thermal energy storage materials. J. Chem. Thermodyn. 2014, 74, 43–50. [Google Scholar] [CrossRef]
- Zeroual, S.; Estellé, P.; Cabaleiro, D.; Vigolo, B.; Emo, M.; Halim, W.; Ouaskit, S. Ethylene glycol based silver nanoparticles synthesized by polyol process: Characterization and thermophysical profile. J. Mol. Liq. 2020, 310, 113229. [Google Scholar] [CrossRef]
- Hamze, S.; Berrada, N.; Cabaleiro, D.; Desforges, A.; Ghanbaja, J.; Gleize, J.; Bégin, D.; Michaux, F.; Maré, T.; Vigolo, B.; et al. Few-layer graphene-based nanofluids with enhanced thermal conductivity. Nanomaterials 2020, 10, 1258. [Google Scholar] [CrossRef]
- Vijande, J.; Piñeiro, M.M.; García, J.; Valencia, J.L.; Legido, J.L. Density and surface tension variation with temperature for heptane + 1-alkanol. J. Chem. Eng. Data 2006, 51, 1778–1782. [Google Scholar] [CrossRef]
- Cabaleiro, D.; Agresti, F.; Barison, S.; Rossi, S.; Bobbo, S.; Fedele, L. Synthesis and characterization of nano-PCM in water for phase-change secondary refrigerants applications. In Proceedings of the Refrigeration Science and Technology, International Institute of Refrigeration, Montreal, Canada, 24–30 August 2019; pp. 1965–1973. [Google Scholar]
- Nakarapanich, J.; Barameesangpet, T.; Suksamranchit, S.; Sirivat, A.; Jamieson, A.M. Rheological properties and structures of cationic surfactants and fatty alcohol emulsions: Effect of surfactant chain length and concentration. Colloid Polym. Sci. 2001, 279, 671–677. [Google Scholar] [CrossRef]
- Colafemmina, G.; Palazzo, G.; Mateos, H.; Amin, S.; Fameau, A.L.; Olsson, U.; Gentile, L. The cooling process effect on the bilayer phase state of the CTAC/cetearyl alcohol/water surfactant gel. Colloids Surfaces A Physicochem. Eng. Asp. 2020, 597, 124821. [Google Scholar] [CrossRef]
- Barry, B.W. The self bodying action of the mixed emulsifier sodium dodecyl sulfate/cetyl alcohol. J. Colloid Interface Sci. 1968, 28, 82–91. [Google Scholar] [CrossRef]
- Ho, C.C.; Goetz, R.J.; El-Aasser, M.S. A biaxial lyotropic nematic phase in dilute solutions of sodium lauryl sulfate-1-hexadecanol-water. Langmuir 1991, 7, 630–635. [Google Scholar] [CrossRef]
- Karl, W.; Perla, R.; Gérard, C.; Franck, C.; Luc, N.M.; Hayat, B.; Denis, F. Effect of surfactant on structure thermal behavior of cetyl stearyl alcohols: DSC and X-ray scattering studies. J. Therm. Anal. Calorim. 2016, 123, 1411–1417. [Google Scholar] [CrossRef]
- Diniz, F.; Marques, C.; Barbosa, T.C.; Martins, D.; Nalone, L.; Costa, S.; Chaud, M.V.; da Silva, C.F.; Souto, E.B.; de Melo Barbosa, R.; et al. dPolymorphism, crystallinity and hydrophilic-lipophilic balance (HLB) of cetearyl alcohol and cetyl alcohol as raw materials for solid lipid nanoparticles (SLN). Asp. Nanotechnol. 2018, 1, 52–60. [Google Scholar] [CrossRef]
- Lunardi, C.N.; Gomes, A.J.; Rocha, F.S.; De Tommaso, J.; Patience, G.S. Experimental methods in chemical engineering: Zeta potential. Can. J. Chem. Eng. 2021, 99, 627–639. [Google Scholar] [CrossRef]
- Tang, B.; Wang, L.; Xu, Y.; Xiu, J.; Zhang, S. Hexadecanol/phase change polyurethane composite as form-stable phase change material for thermal energy storage. Sol. Energy Mater. Sol. Cells 2016, 144, 1–6. [Google Scholar] [CrossRef]
- Métivaud, V.; Lefèvre, A.; Ventolà, L.; Négrier, P.; Moreno, E.; Calvet, T.; Mondieig, D.; Cuevas-Diarte, M.A. Hexadecane (C16H34) + 1-Hexadecanol (C16H33OH) binary system: Crystal structures of the components and experimental phase diagram. application to thermal protection of liquids. Chem. Mater. 2005, 17, 3302–3310. [Google Scholar] [CrossRef]
- Shang, Y.; Zhang, D. Preparation and characterization of three-dimensional graphene network encapsulating 1-hexadecanol composite. Appl. Therm. Eng. 2017, 111, 353–357. [Google Scholar] [CrossRef]
- Mosselman, C.; Mourik, J.; Dekker, H. Enthalpies of phase change and heat capacities of some long-chain alcohols. Adiabatic semi-microcalorimeter for studies of polymorphism. J. Chem. Thermodyn. 1974, 6, 477–487. [Google Scholar] [CrossRef]
- Xing, J.; Tan, Z.C.; Shi, Q.; Tong, B.; Wang, S.X.; Li, Y.S. Heat capacity and thermodynamic properties of 1-hexadecanol. J. Therm. Anal. Calorim. 2008, 92, 375–380. [Google Scholar] [CrossRef]
- Sosa, F.H.B.; Carareto, N.D.D.; Maximo, G.J.; Meirelles, A.J.D.A.; Costa, M.C. Solid-liquid equilibrium of binary systems containing fatty acids and fatty alcohols using differential scanning calorimetry. J. Chem. Eng. Data 2019, 64, 5017–5027. [Google Scholar] [CrossRef]
- de Matos, F.C.; da Costa, M.C.; de Meirelles, A.J.; Batista, E.A.C. Binary solid-liquid equilibrium systems containing fatty acids, fatty alcohols and trilaurin by differential scanning calorimetry. Fluid Phase Equilib. 2016, 423, 74–83. [Google Scholar] [CrossRef]
- Maximo, G.J.; Carareto, N.D.D.; Costa, M.C.; dos Santos, A.O.; Cardoso, L.P.; Krähenbühl, M.A.; Meirelles, A.J.A. On the solid-liquid equilibrium of binary mixtures of fatty alcohols and fatty acids. Fluid Phase Equilib. 2014, 366, 88–98. [Google Scholar] [CrossRef]
- Acree, W.; Chickos, J.S. Phase transition enthalpy measurements of organic and organometallic compounds. Sublimation, vaporization and fusion enthalpies from 1880 to 2015. Part 1. C1-C10. J. Phys. Chem. Ref. Data 2016, 45, 033101. [Google Scholar] [CrossRef]
- Mu, R.; Malhotra, V.M. Effects of surface and physical confinement on the phase transitions of cyclohexane in porous silica. Phys. Rev. B 1991, 44, 4296–4303. [Google Scholar] [CrossRef]
- Gelb, L.D.; Gubbins, K.E.; Radhakrishnan, R.; Christenson, H.K. Confinement effects on freezing and melting. J. Phys. Condens. Matter 2001, 13, 95–133. [Google Scholar] [CrossRef]
- Yang, L.; Liu, S.; Zheng, H. A comprehensive review of hydrodynamic mechanisms and heat transfer characteristics for microencapsulated phase change slurry (MPCS) in circular tube. Renew. Sustain. Energy Rev. 2019, 114, 109312. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties (REFPROP), Version 9.0. Physical and Chemical Properties. 2010. Available online: https://www.bibsonomy.org/bibtex/2ae369b98c7cc721f7e4eb576d6dee1e7/thorade (accessed on 28 November 2021).
- Fu, Y.; Meng, X.; Liang, X.; Wu, J. Measurements of density and viscosity of 1-hexadecanol in the temperature range from (328.15 to 623.15) K at pressures up to 10 MPa. J. Chem. Thermodyn. 2021, 152, 106263. [Google Scholar] [CrossRef]
- Macosko, C.W. Rheology. Principles, Measurements and Applications; Wiley-VCH: Weinheim, Germany, 1994; ISBN 1560815795. [Google Scholar]
- Vogel, H. The law of the relation between the viscosity of liquids and the temperature. Phys. Z. 1921, 22, 645–646. [Google Scholar]
- Fulcher, G.S. Analysis of recent measurements of the viscosity of glasses. J. Am. Ceram. Soc 1925, 8, 339–355. [Google Scholar] [CrossRef]
- Tammann, G.; Hesse, W. The dependence of viscosity upon the temperature of supercooled liquids. Z. Anorg. Allg. Chem. 1926, 156, 245–257. [Google Scholar] [CrossRef]
- Huang, X.; Alva, G.; Liu, L.; Fang, G. Microstructure and thermal properties of cetyl alcohol/high density polyethylene composite phase change materials with carbon fiber as shape-stabilized thermal storage materials. Appl. Energy 2017, 200, 19–27. [Google Scholar] [CrossRef]
- Atinafu, D.G.; Dong, W.; Wang, C.; Wang, G. Synthesis of porous carbon from cotton using an Mg(OH)2 template for form-stabilized phase change materials with high encapsulation capacity, transition enthalpy and reliability. J. Mater. Chem. A 2018, 6, 8969–8977. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism, 3rd ed.; Oxford University Press: London, UK, 1882. [Google Scholar]
- Hashin, Z.; Shtrikman, S. A Variational approach to the theory of the effective magnetic permeability of multiphase materials. J. Appl. Phys. 1962, 33, 3125–3131. [Google Scholar] [CrossRef]
- Kawanami, T.; Togashi, K.; Fumoto, K.; Hirano, S.; Zhang, P.; Shirai, K.; Hirasawa, S. Thermophysical properties and thermal characteristics of phase change emulsion for thermal energy storage media. Energy 2016, 117, 562–568. [Google Scholar] [CrossRef]
- Lenahan, F.D.; Zikeli, M.; Rausch, M.H.; Klein, T.; Fröba, A.P. Viscosity, interfacial tension, and density of binary-liquid mixtures of n-hexadecane with n-octacosane, 2,2,4,4,6,8,8-heptamethylnonane, or 1-hexadecanol at temperatures between 298.15 and 573.15 K by Surface Light Scattering and Equilibrium Molecular Dy. J. Chem. Eng. Data 2021, 66, 2264–2280. [Google Scholar] [CrossRef]









| Main Formulation Parameters | 1st Day | 30th Day | |||
|---|---|---|---|---|---|
| C16OH (Final wt.%) | Nucleating Agent (Final wt.%) | SDS + SDBS + Brij 30 (Final wt.%) | ζeta Potential | Size (pdi) | Size (pdi) |
| 2 wt.% | - | 0.25 wt.% | −44 mV | 107 nm (0.25) | 106 nm (0.21) |
| 4 wt.% | - | 0.50 wt.% | −56 mV | 123 nm (0.24) | 124 nm (0.21) |
| 6 wt.% | - | 0.75 wt.% | −63 mV | 123 nm (0.24) | 121 nm (0.21) |
| 8 wt.% | - | 1.00 wt.% | −68 mV | 152 nm (0.30) | 168 nm (0.41) |
| 1.8 wt.% | C20OH (0.2 wt.%) | 0.25 wt.% | −46 mV | 102 nm (0.22) | 106 nm (0.22) |
| 3.6 wt.% | C20OH (0.4 wt.%) | 0.50 wt.% | −54 mV | 126 nm (0.28) | 131 nm (0.30) |
| 5.4 wt.% | C20OH (0.6 wt.%) | 0.75 wt.% | −62 mV | 139 nm (0.31) | 160 nm (0.36) |
| 7.2 wt.% | C20OH (0.8 wt.%) | 1.00 wt.% | −66 mV | 162 nm (0.31) | 176 nm (0.36) |
| 1.96 wt.% | SiO2 (0.04 wt.%) | 0.25 wt.% | −42 mV | 152 nm (0.14) | 157 nm (0.17) |
| 3.92 wt.% | SiO2 (0.08 wt.%) | 0.50 wt.% | −50 mV | 173 nm (0.17) | 178 nm (0.17) |
| 5.88 wt.% | SiO2 (0.12 wt.%) | 0.75 wt.% | −61 mV | 186 nm (0.19) | 189 nm (0.18) |
| 7.84 wt.% | SiO2 (0.16 wt.%) | 1.00 wt.% | −68 mV | 214 nm (0.21) | 220 nm (0.21) |
| Main Formulation Parameters | Cooling | Heating | |||
|---|---|---|---|---|---|
| C16OH (Final wt.%) | Nucleating Agent (Final wt.%) | SDS + SDBS + Brij30 (Final wt.%) | T (K) ‡ | T (K) ‡ | Δh (J·g−1) * |
| bulk C16OH | 321.6/316.4 | 321.9 | 212.7 | ||
| 2 wt.% | - | 0.25 wt.% | 311.3/306.6 p | 319.9 | 2.75 |
| 4 wt.% | - | 0.50 wt.% | 312.1/306.4 p | 320.1/327.6 p | 5.64 |
| 6 wt.% | - | 0.75 wt.% | 313.4/308.3 p/305.5 p | 320.9/327.4 p | 8.06 |
| 8 wt.% | - | 1.00 wt.% | 312.9/308.1 p/305.9 p | 320.3/327.2 p | 11.54 |
| 1.8 wt.% | C20OH (0.2 wt.%) | 0.25 wt.% | 320.3/314.5 p | 320.6/328.8 p | 2.46 |
| 3.6 wt.% | C20OH (0.4 wt.%) | 0.50 wt.% | 320.4/314.6 p | 320.7/328.9 p | 5.33 |
| 5.4 wt.% | C20OH (0.6 wt.%) | 0.75 wt.% | 320.5/314.8 p | 320.5/329.0 p | 7.46 |
| 7.2 wt.% | C20OH (0.8 wt.%) | 1.00 wt.% | 320.8/315.0 p | 320.4/328.8 p | 10.88 |
| 1.96 wt.% | SiO2 (0.04 wt.%) | 0.25 wt.% | 313.7 | 320.0 | 2.35 |
| 3.92 wt.% | SiO2 (0.08 wt.%) | 0.50 wt.% | 313.5 | 320.1/323.5 p | 5.20 |
| 5.88 wt.% | SiO2 (0.12 wt.%) | 0.75 wt.% | 313.4 | 320.0/323.0 p | 7.22 |
| 7.84 wt.% | SiO2 (0.16 wt.%) | 1.00 wt.% | 313.3 | 320.2/323.1 p | 10.01 |
| Parameter | Phosphate Buffer Solution, PBS, (0.04 M) | Water-Based Emulsions | |||||
|---|---|---|---|---|---|---|---|
| C16OH (2 wt.%) | C16OH (4 wt.%) | C16OH (6 wt.%) | C16OH (8 wt.%) | C16OH (7.8 wt.%) + C20OH (0.2 wt.%) | C16OH (7.84 wt.%) + SiO2 (0.16 wt.%) | ||
| η0/mPa·s | 0.00162 | 0.00213 | 0.00281 | 0.00328 | 0.00473 | 0.00480 | 0.00542 |
| D | 75.182 | 75.208 | 75.257 | 75.280 | 75.297 | 75.247 | 75.245 |
| T0/K | 23.175 | 23.167 | 23.152 | 23.145 | 23.132 | 23.155 | 23.156 |
| s/mPa·s | 0.037 | 0.045 | 0.066 | 0.061 | 0.046 | 0.048 | 0.047 |
| AAD% | 1.4% | 1.9% | 2.9% | 2.5% | 1.1% | 1.7% | 1.8% |
| Parameter | Phosphate Buffer Solution, PBS, (0.04 M) | Water-Based Nanoemulsions | ||||
|---|---|---|---|---|---|---|
| C16OH (2 wt.%) | C16OH (4 wt.%) | C16OH (6 wt.%) | C16OH (8 wt.%) | C16OH (7.8 wt.%) + C20OH (0.2 wt.%) | ||
| 283.15 K ≤ T ≤ 353.15 K | 283.15 K ≤ T ≤ 313.15 K (fatty alcohol droplets are solid) | |||||
| A0/g·cm−3 | 0.7549 | 0.7301 | 0.7437 | 0.7750 | 0.7618 | 0.7925 |
| 103·A1/g·cm−3·K−1 | 1.895 | 2.039 | 1.941 | 1.711 | 1.786 | 1.586 |
| −106·A2/g·cm−3·K−2 | 3.614 | 3.857 | 3.714 | 3.333 | 3.476 | 3.143 |
| AAD% | 0.12% | 0.14% | 0.11% | 0.11% | 0.13% | 0.12% |
| 328.15 K ≤ T ≤ 353.15 K (fatty alcohol droplets are liquid) | ||||||
| A0/g·cm−3 | 0.6829 | 0.6802 | 0.7437 | 0.6891 | 0.6493 | |
| 103·A1/g·cm−3·K−1 | 2.296 | 2.291 | 1.896 | 2.188 | 2.429 | |
| −106·A2/g·cm−3·K−2 | 4.214 | 4.214 | 3.643 | 4.071 | 4.429 | |
| AAD% | 0.11% | 0.10% | 0.11% | 0.11% | 0.11% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cabaleiro, D.; Losada-Barreiro, S.; Agresti, F.; Hermida-Merino, C.; Fedele, L.; Lugo, L.; Barison, S.; Piñeiro, M.M. Development and Thermophysical Profile of Cetyl Alcohol-in-Water Nanoemulsions for Thermal Management. Fluids 2022, 7, 11. https://doi.org/10.3390/fluids7010011
Cabaleiro D, Losada-Barreiro S, Agresti F, Hermida-Merino C, Fedele L, Lugo L, Barison S, Piñeiro MM. Development and Thermophysical Profile of Cetyl Alcohol-in-Water Nanoemulsions for Thermal Management. Fluids. 2022; 7(1):11. https://doi.org/10.3390/fluids7010011
Chicago/Turabian StyleCabaleiro, David, Sonia Losada-Barreiro, Filippo Agresti, Carolina Hermida-Merino, Laura Fedele, Luis Lugo, Simona Barison, and Manuel M. Piñeiro. 2022. "Development and Thermophysical Profile of Cetyl Alcohol-in-Water Nanoemulsions for Thermal Management" Fluids 7, no. 1: 11. https://doi.org/10.3390/fluids7010011
APA StyleCabaleiro, D., Losada-Barreiro, S., Agresti, F., Hermida-Merino, C., Fedele, L., Lugo, L., Barison, S., & Piñeiro, M. M. (2022). Development and Thermophysical Profile of Cetyl Alcohol-in-Water Nanoemulsions for Thermal Management. Fluids, 7(1), 11. https://doi.org/10.3390/fluids7010011