Air Entrainment in Drop Shafts: A Novel Approach Based on Machine Learning Algorithms and Hybrid Models
Abstract
:1. Introduction
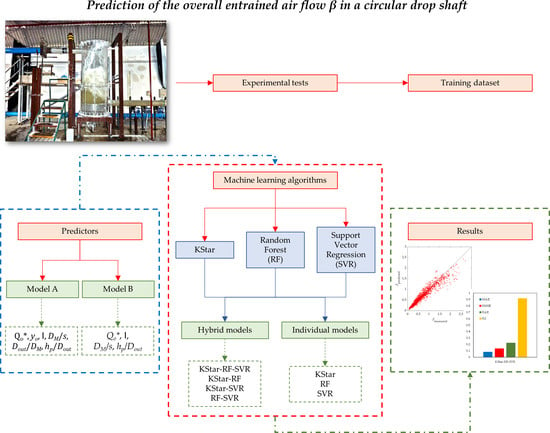
2. Materials and Methods
2.1. The Experimental Setup
2.2. Base Models
2.2.1. Random Forest
2.2.2. Support Vector Regression
2.2.3. KStar
2.3. Hybrid Models, Evaluation Metrics, and Cross-Validation
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
List of Symbols
| a | = | KStar—generic instance |
| b | = | KStar—generic instance |
| b | = | Support vector machine—bias |
| C | = | Support vector machine—constant |
| Din | = | Upstream pipe diameter |
| DM | = | Drop shaft diameter |
| Dout | = | Outlet pipe diameter |
| F | = | Support vector machine—feature space |
| g | = | Gravitational acceleration |
| ho | = | Incoming flow depth |
| hp | = | Pool depth |
| i | = | KStar—absolute difference between first and last instance |
| I | = | Impact number |
| k | = | Support vector machine—kernel function |
| K* | = | KStar—distance in the complexity computation |
| N | = | Random forest—number of units in the node t |
| P* | = | KStar—probability of all paths from instance a to instance b |
| Q | = | Water discharge |
| Qo* | = | Nondimensional water discharge |
| R | = | Random forest—mean square error in the node t |
| S | = | KStar—model parameter |
| s | = | Drop height |
| t | = | Random forest—generic node |
| V | = | Flow velocity |
| w | = | Support vector machine—weight |
| X | = | Support vector machine—space of the input arrays |
| xi | = | Support vector machine—experimental input values |
| yi | = | Random forest—value assumed by the target variable in the i-th unit |
| yi | = | Support vector machine—experimental target values |
| ym | = | Random forest—average value of the target variable in the node t |
| yo | = | Upstream pipe filling ratio |
| ε | = | Support vector machine—maximum deviation from the experimental target values yi |
| σ | = | Support vector machine—PUK parameter from which the peak tailing factor depends |
| ω | = | Support vector machine—PUK parameter from which the peak half-width depends |
| b | = | Dimensionless entrained airflow |
| ξι | = | Support vector machine—slack variable |
References
- Christodoulou, G.C. Drop manholes in supercritical pipelines. J. Irrig. Drain. Eng. 1991, 117, 37–47. [Google Scholar] [CrossRef]
- Rajaratnam, N.; Mainali, A.; Hsung, C.Y. Observations on flow in vertical dropshafts in urban drainage systems. J. Environ. Eng. 1997, 123, 486–491. [Google Scholar] [CrossRef]
- Chanson, H. Hydraulics of rectangular dropshafts. J. Irrig. Drain. Eng. 2004, 130, 523–529. [Google Scholar] [CrossRef] [Green Version]
- Carvalho, R.F.; Leandro, J. Hydraulic characteristics of a drop square manhole with a downstream control gate. J. Irrig. Drain. Eng. 2012, 138, 569–576. [Google Scholar] [CrossRef]
- Granata, F.; de Marinis, G.; Gargano, R. Flow-improving elements in circular drop manholes. J. Hydraul. Res. 2014, 52, 347–355. [Google Scholar] [CrossRef]
- Granata, F. Dropshaft cascades in urban drainage systems. Water Sci. Technol. 2016, 73, 2052–2059. [Google Scholar] [CrossRef]
- Ma, Y.; Zhu, D.Z.; Rajaratnam, N.; van Duin, B. Energy dissipation in circular drop manholes. J. Irrig. Drain. Eng. 2017, 143, 04017047. [Google Scholar] [CrossRef]
- Granata, F.; de Marinis, G.; Gargano, R.; Hager, W.H. Hydraulics of circular drop manholes. J. Irrig. Drain. Eng. 2011, 137, 102–111. [Google Scholar] [CrossRef]
- Granata, F.; de Marinis, G.; Gargano, R. Air-water flows in circular drop manholes. Urban Water J. 2015, 12, 477–487. [Google Scholar] [CrossRef]
- Ma, Y.; Zhu, D.Z.; Rajaratnam, N. Air entrainment in a tall plunging flow dropshaft. J. Hydraul. Eng. 2016, 142, 04016038. [Google Scholar] [CrossRef]
- Azamathulla, H.M.; Haghiabi, A.H.; Parsaie, A. Prediction of side weir discharge coefficient by support vector machine technique. Water Sci. Technol. Water Supply 2016, 16, 1002–1016. [Google Scholar] [CrossRef] [Green Version]
- Roushangar, K.; Khoshkanar, R.; Shiri, J. Predicting trapezoidal and rectangular side weirs discharge coefficient using machine learning methods. ISH J. Hydraul. Eng. 2016, 22, 254–261. [Google Scholar] [CrossRef]
- Azimi, H.; Bonakdari, H.; Ebtehaj, I. Design of radial basis function-based support vector regression in predicting the discharge coefficient of a side weir in a trapezoidal channel. Appl. Water Sci. 2019, 9, 78. [Google Scholar] [CrossRef] [Green Version]
- Granata, F.; Di Nunno, F.; Gargano, R.; de Marinis, G. Equivalent discharge coefficient of side weirs in circular channel—A lazy machine learning approach. Water 2019, 11, 2406. [Google Scholar] [CrossRef] [Green Version]
- Etemad-Shahidi, A.; Yasa, R.; Kazeminezhad, M.H. Prediction of wave-induced scour depth under submarine pipelines using machine learning approach. Appl. Ocean Res. 2011, 33, 54–59. [Google Scholar] [CrossRef] [Green Version]
- Najafzadeh, M.; Azamathulla, H.M. Neuro-fuzzy GMDH to predict the scour pile groups due to waves. J. Comput. Civ. Eng. 2015, 29, 04014068. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Etemad-Shahidi, A.; Lim, S.Y. Scour prediction in long contractions using ANFIS and SVM. Ocean Eng. 2016, 111, 128–135. [Google Scholar] [CrossRef]
- Di Nunno, F.; Alves Pereira, F.; de Marinis, G.; Di Felice, F.; Gargano, R.; Miozzi, M.; Granata, F. Deformation of Air Bubbles Near a Plunging Jet Using a Machine Learning Approach. Appl. Sci. 2020, 10, 3879. [Google Scholar] [CrossRef]
- Zhang, Y.; Azman, A.N.; Xu, K.W.; Kang, C.; Kim, H.B. Two-phase flow regime identification based on the liquid-phase velocity information and machine learning. Exp. Fluids 2020, 61, 1–16. [Google Scholar] [CrossRef]
- Sujjaviriyasup, T.; Pitiruek, K. Hybrid ARIMA-Support Vector Machine Model for Agricultural Production Planning. Appl. Math. Sci. 2013, 7, 2833–2840. [Google Scholar] [CrossRef]
- Gala, Y.; Fernández, A.; Díaz, J.; Dorronsoro, J.R. Hybrid machine learning forecasting of solar radiation values. Neurocomputing 2016, 176, 48–59. [Google Scholar] [CrossRef]
- Khozani, Z.S.; Khosravi, K.; Pham, B.T.; Kløve, B.; Mohtar, W.H.M.W.; Yaseen, Z.M. Determination of compound channel apparent shear stress: Application of novel data mining models. J. Hydroinform. 2019, 21, 798–811. [Google Scholar] [CrossRef] [Green Version]
- Kombo, O.H.; Kumaran, S.; Sheikh, Y.H.; Bovim, A.; Jayavel, K. Long-Term Groundwater Level Prediction Model Based on Hybrid KNN-RF Technique. Hydrology 2020, 7, 59. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Cleary, J.G.; Trigg, L.E. K*: An instance-based learner using an entropic distance measure. In Machine Learning Proceedings 1995; Morgan Kaufmann: San Francisco, CA, USA, 1995; pp. 108–114. [Google Scholar]
- Kittler JHatef, M.; Duin, R.P.W.; Matas, J. On Combining Classifiers. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 226–239. [Google Scholar] [CrossRef] [Green Version]
- Quinlan, J.R. Learning with continuous classes. In Proceedings of the 5th Australian Joint Conference on Artificial Intelligence, Hobart, Australia, 16–18 November 1992; Volume 92, pp. 343–348. [Google Scholar]
- Granata, F.; de Marinis, G. Machine learning methods for wastewater hydraulics. Flow Meas. Instrum. 2017, 57, 1–9. [Google Scholar] [CrossRef]










| Coefficient of Determination: it represents a measure of the model accuracy, assessing how well the model fits the experimental results. | |
| Mean Absolute Error: it provides the average error magnitude for the predicted values. | |
| Root-Mean-Squared Error: it provides the square root of the average squared errors for the predicted values. It has the benefit of penalizing large errors. | |
| Relative Absolute Error: it provides the normalized total absolute error with respect to the sum of the difference between the mean and each measured value. | |
| In the above formulas, m is the total number of experimental data, fi is the predicted value for the i-th data point, yi is the measured value for the i-th data point, ya is the averaged value of the experimental data. | |
| Qo* | yo | I | DM/s | hp/Dout | b | |
|---|---|---|---|---|---|---|
| Minimum Value | 0.027 | 0.158 | 0.234 | 0.167 | 0.258 | 0.029 |
| First Quartile | 0.135 | 0.295 | 0.728 | 0.320 | 0.639 | 0.349 |
| Median | 0.294 | 0.385 | 0.998 | 0.480 | 0.985 | 0.573 |
| Third Quartile | 0.507 | 0.503 | 1.607 | 0.667 | 1.636 | 0.930 |
| Maximum Value | 1.417 | 0.950 | 6.374 | 2.000 | 4.600 | 2.709 |
| Mean | 0.352 | 0.406 | 1.309 | 0.578 | 1.199 | 0.694 |
| Standard Deviation | 0.265 | 0.139 | 0.895 | 0.401 | 0.725 | 0.473 |
| Skewness | 0.657 | 0.444 | 1.043 | 0.730 | 0.885 | 0.770 |
| Model | Predictors | Algorithm | R2 | MAE | RMSE | RAE (%) |
|---|---|---|---|---|---|---|
| A | Qo*, yo, I, DM/s, Dout/DM, hp/Dout | Hyb_KStar–RF–SVR | 0.917 | 0.083 | 0.136 | 22.47 |
| Hyb_KStar–RF | 0.905 | 0.092 | 0.146 | 24.68 | ||
| Hyb_KStar–SVR | 0.909 | 0.086 | 0.142 | 23.31 | ||
| Hyb_RF–SVR | 0.909 | 0.089 | 0.143 | 24.03 | ||
| KStar | 0.887 | 0.099 | 0.159 | 26.59 | ||
| RF | 0.882 | 0.104 | 0.163 | 28.03 | ||
| SVR | 0.888 | 0.098 | 0.159 | 26.38 | ||
| B | Qo*, I, DM/s, hp/Dout | Hyb_KStar–RF–SVR | 0.888 | 0.096 | 0.158 | 25.92 |
| Hyb_KStar–RF | 0.877 | 0.102 | 0.166 | 27.58 | ||
| Hyb_KStar–SVR | 0.854 | 0.105 | 0.181 | 28.22 | ||
| Hyb_RF–SVR | 0.883 | 0.098 | 0.162 | 26.53 | ||
| KStar | 0.799 | 0.127 | 0.212 | 34.21 | ||
| RF | 0.875 | 0.108 | 0.167 | 29.09 | ||
| SVR | 0.818 | 0.121 | 0.202 | 32.58 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Granata, F.; Di Nunno, F. Air Entrainment in Drop Shafts: A Novel Approach Based on Machine Learning Algorithms and Hybrid Models. Fluids 2022, 7, 20. https://doi.org/10.3390/fluids7010020
Granata F, Di Nunno F. Air Entrainment in Drop Shafts: A Novel Approach Based on Machine Learning Algorithms and Hybrid Models. Fluids. 2022; 7(1):20. https://doi.org/10.3390/fluids7010020
Chicago/Turabian StyleGranata, Francesco, and Fabio Di Nunno. 2022. "Air Entrainment in Drop Shafts: A Novel Approach Based on Machine Learning Algorithms and Hybrid Models" Fluids 7, no. 1: 20. https://doi.org/10.3390/fluids7010020
APA StyleGranata, F., & Di Nunno, F. (2022). Air Entrainment in Drop Shafts: A Novel Approach Based on Machine Learning Algorithms and Hybrid Models. Fluids, 7(1), 20. https://doi.org/10.3390/fluids7010020