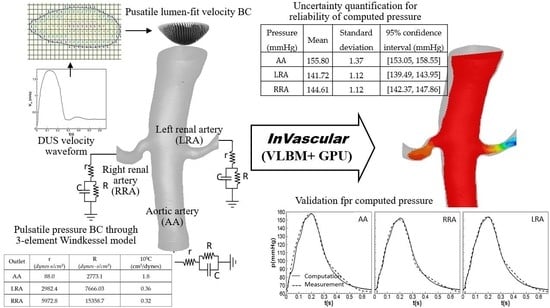
Inlet and Outlet Boundary Conditions and Uncertainty Quantification in Volumetric Lattice Boltzmann Method for Image-Based Computational Hemodynamics

Abstract

Inlet and outlet boundary conditions (BCs) play an important role in newly emerged image-based computational hemodynamics for blood flows in human arteries anatomically extracted from medical images. We developed physiological inlet and outlet BCs based on patients’ medical data and integrated them into the volumetric lattice Boltzmann method. The inlet BC is a pulsatile paraboloidal velocity profile, which fits the real arterial shape, constructed from the Doppler velocity waveform. The BC of each outlet is a pulsatile pressure calculated from the three-element Windkessel model, in which three physiological parameters are tuned by the corresponding Doppler velocity waveform. Both velocity and pressure BCs are introduced into the lattice Boltzmann equations through Guo’s non-equilibrium extrapolation scheme. Meanwhile, we performed uncertainty quantification for the impact of uncertainties on the computation results. An application study was conducted for six human aortorenal arterial systems. The computed pressure waveforms have good agreement with the medical measurement data. A systematic uncertainty quantification analysis demonstrates the reliability of the computed pressure with associated uncertainties in the Windkessel model. With the developed physiological BCs, the image-based computation hemodynamics is expected to provide a computation potential for the noninvasive evaluation of hemodynamic abnormalities in diseased human vessels.

1. Introduction

With the recent advances in medical imaging, computational power, and mathematical algorithms, image-based computational hemodynamics (ICHD) has emerged [1,2,3,4,5,6,7] as a new capability giving rise to the potential for computation-aided diagnostics and therapeutics in a patient-specific environment for cardiovascular diseases. Based on radiological imaging data, such as computed tomography angiography (CTA) images and Doppler ultrasound (DUS) velocity waveforms, ICHD enables noninvasive and patient-specific quantification of pulsatile hemodynamics in human vessels. Such data, including velocity vector, pressure, vorticity vector, and wall-shear stress (WSS) in the entire artery segment with fine spatial and temporal resolutions, are not readily available from the current standard clinical measurements. Through further postprocessing of the pulsatile hemodynamic data, either the assessment of the true hemodynamic abnormality or the prediction of potential therapeutic/surgical outcomes from an interventional treatment may aid in clinical decision-making for various cardiovascular diseases.

A typical ICHD from medical data to medical insights mainly consists of three steps. They are (1) image extractions of a three-dimensional anatomical geometry of the diseased artery from CTA data and one-dimensional velocity waveforms from DUS images at inlet and outlets, (2) computation of pulsatile hemodynamics employing physical parameters together with the flow environment, and (3) post-processing of the computed pulsatile hemodynamics with analysis, visualization, and parametrization to the key insights of the disease assessment and potential therapeutic outcomes. Since only a segment of the blood circulation system is being computed, boundary conditions (BCs) are required to be applied at the inlet(s) and outlet(s) of the vessel segment to represent the remaining vascular network. In general, the introduction of the inlet BC is relatively straightforward, imposing parabolic-like flow profiles at the cross-section of the inlet. Usually, an inlet cross-section of a human vessel is not a perfect circle. Therefore, neither a steady Poiseuille-Hagen nor an oscillating Womersley velocity profile can be directly constructed based on a DUS-measured velocity waveform. The choices of the outflow BC in ICHD vary among zero pressure or zero traction conditions, resistance or impedance conditions, reduced-order models which can be an open or closed loop, and reduced-order one-dimensional wave propagation equations [8,9,10]. To capture the interaction between the local three-dimensional artery segment and the one-dimensional global circulation, the three-dimensional flow solver must be coupled to a reduced-order lumped parameter network model. Among them, the three-element Windkessel model [11,12,13,14,15] (WK3) has been commonly used to construct such a network, in which a Windkessel circuit is adopted to model the distal vasculature with one capacitor, modeling vessel compliance, and two resistors, modeling proximal and distal flow resistances, respectively. Evidence has shown that the WK3 can well reproduce physiological pressure waveforms [16,17] in large vessels.

In this work, we present the physiological inlet and outlet BCs in volumetric lattice Boltzmann method (VLBM) [18] for ICHD together with uncertainty quantification (UQ). The lattice Boltzmann method (LBM) [19,20] is a class of computational fluid dynamics (CFD) methods for solving complex flows. Instead of directly solving a set of nonlinear partial differential equations, i.e., Navier-stokes (NS) equations, the LBM is a discretized kinetic model on a regular lattice to solve the dynamics of incompressible fluid flow. Due to its particulate nature and local dynamics, the LBM has its advantages over the NS-based CFD methods, especially in dealing with complex boundaries [18,21], incorporating microscopic interactions [22,23] in multiphase flows, and implementing GPU (Graphics Processing Unit) parallel computing [21,24]. Nevertheless, the LBM has not been extensively used for ICHD so far and the majority of attempts have imposed non-physiological BCs. An example is the zero pressure BC [25,26,27,28] at the outlets. The zero pressure BC, although easy to be implemented, is well known to lead to unrealistic hemodynamics, in part because of its inability to capture physiologic levels of pressure [6]. Few other studies have used the fully developed BC [18,29] at the outlets, which is also inappropriate for a pulsatile flow in arbitrary flow domains. In this paper, we develop the physiological velocity BC at the inlet based on the DUS waveform and pressure BC at each outlet via WK3 model tuned by the corresponding DUS waveform and then integrated them into the VLBM. We study six aortorenal arterial systems, with given CTA image data and DUS velocity waveforms of each, for noninvasive quantification of pulsatile hemodynamics. To demonstrate the accuracy of the computation, we compare the computed pressure waves with the corresponding invasive pressure measurements during digital subtraction angiography (DSA) in the clinic. Meanwhile, we perform uncertainty quantification to demonstrate the reliability of the computation.

2. Methods and Materials

We have previously developed and validated a VLBM solver [30] for solving image-based pore-scale porous media flows. The solver synergistically employs the traditional node-based LBM for image segmentation and the cell-based VLBM [18] for CFD, enabling a seamless connection between these two parts and unified GPU parallelization for fast computation [21,31,32].

The VLBM is formulated on a cell-based mesh. Fluid particles are uniformly distributed in lattice cells, as opposed to sitting at lattice nodes in conventional LBM. As schematized in Figure 1, an arbitrary boundary (black line) separates a fluid domain (without dots) from a solid boundary structure (with dots). Three distinct cells are characterized through a volumetric parameter, i.e., the occupation of solid volume $\Delta V_s\left(\mathit{x}\right)$ in the cell with total volume $\Delta V\left(\mathit{x}\right)$, defined as $\mathcal{P}\left(\mathit{x}\right)\equiv \Delta V_s\left(\mathit{x}\right)/\Delta V\left(\mathit{x}\right)$. Thus three different cells, fluid cell ($\mathcal{P}=0$), solid cell ($\mathcal{P}=1$), and boundary cell ($0<\mathcal{P}<1$), can be distinguished.

On a lattice space with b directions of discrete molecular velocity, VLBM deals with the time evolution of the particle population, $n_i\left(\mathit{x},t\right)$, corresponding to the ith velocity ${\mathit{e}}_i$

$$n_i\left(\mathit{x}+{\mathit{e}}_i\delta t,t+\delta t\right)=n_i\left(\mathit{x},t\right)-\frac{\left[n_i\left(\mathit{x},t\right)-n_i^{eq}\left(\mathit{x},t\right)\right]}{\tau };i=0,\dots , b$$

(1)

where $n_i^{eq}\left(\mathit{x},t\right)$ and $\tau$ are the corresponding equilibrium particle population and relaxation time, respectively. The resulting density $\rho \left(\mathit{x},t\right)$ and velocity $\mathit{u}\left(\mathit{x},t\right)$ in the fluid domain are

$$\rho \left(\mathit{x},t\right)=\sum n_i\left(\mathit{x},t\right)/\left[1-\mathcal{P}\left(\mathit{x},t\right)\right]$$

(2)

and

$$\mathit{u}\left(\mathit{x},t\right)=\sum {\mathit{e}}_i{n}_i\left(\mathit{x},t\right)/\sum n_i\left(\mathit{x},t\right)$$

(3)

The pressure field $p\left(\mathit{x},t\right)$ is then calculated from:

$$p\left(\mathit{x},t\right)-p_0=c_s^2\left[\rho \left(\mathit{x},t\right)-{\rho }_0\right]$$

(4)

where $p_0$ and ${\rho }_0$ are reference pressure and density, respectively. In this work, we adapted the VLBM solver to ICHD, named InVascular, based on medical imaging data.

The implementation flow chart of InVascular is shown in Figure 2. It starts with the image segmentation from CTA image data to extract the anatomical geometry using the conventional LBM with D3Q7 lattice model [33]. A distance field [34] governed by a level set equation [35] is solved in which the zero-level distance represents the morphological boundary of the vessel segment. From the distance field, $\mathcal{P}\left(\mathit{x}\right)$ of each cell is calculated and then, together with the inlet and outlet BCs, fed to VLBM [18] with D3Q19 lattice model. Both image segmentation and computational hemodynamics (dashed part in Figure 2) are carried out on a unified mesh and connected seamlessly. Thus the state-of-the-art GPU parallelism can be efficiently utilized. The detailed formulation of LBM for image segmentation and VLBM computational hemodynamics, as well as the connection between them, and the GPU parallelization are referred to in our published papers [21,30]. In this paper, we focus on the integration of the physiological inlet and outlet BCs with the VLBM, as highlighted in Figure 2.

2.1. Physiological Inlet and Outlet Boundary Conditions

In this part, we present the algorithms to construct the physiological inlet and outlet BCs based on the DUS velocity waveforms. The inlet BC is a velocity profile, and the output BC is a pressure calculated from WK3. Both velocity and pressure BCs are introduced into VLBM.

2.1.1. Implementation of Velocity and Pressure BCs in VLBM

In the VLBM, we employed the non-equilibrium extrapolation boundary condition developed by Guo et al. [36] as follows.

$$n_i\left({\mathit{x}}_b,t\right)-n_i^{eq}\left({\mathit{x}}_b,t\right)=n_i\left({\mathit{x}}_f,t\right)-n_i^{eq}\left({\mathit{x}}_f,t\right)$$

(5)

for i-th direction where ${\mathit{x}}_b$ and ${\mathit{x}}_f$ are the boundary cell and its next fluid cell along that direction, respectively. If the velocity, $\mathit{u}\left({\mathit{x}}_b,t\right)$, is known at the boundary cell, the velocity BC is:

$$n_i\left({\mathit{x}}_b,t\right)=n_i^{eq}\left(\rho \left({\mathit{x}}_f, t\right),\mathit{u}\left({\mathit{x}}_b,t\right)\right)+n_i\left({\mathit{x}}_f,t\right)-n_i^{eq}\left({\mathit{x}}_f,t\right)$$

(6)

Whereas if the pressure $p\left({\mathit{x}}_b,t\right)$ is given at the boundary cell, the pressure BC reads:

$$n_i\left({\mathit{x}}_b,t\right)=n_i^{eq}\left(\rho \left({\mathit{x}}_b,t\right),\mathit{u}\left({\mathit{x}}_f, t\right)\right)+n_i\left({\mathit{x}}_f,t\right)-n_i^{eq}\left({\mathit{x}}_f,t\right)$$

(7)

where $\rho \left({\mathit{x}}_b,t\right)$ is calculated from Equation (4). We use the velocity BC and pressure BC at the inlet and each outlet, respectively.

In InVascular, the inlet and outlet BCs are based on the patient’s DUS data, as shown by the shaded part in Figure 2. We present the introduction of the inlet and outlet BCs in the following subsections.

2.1.2. Lumen-Fitted Velocity BC Profile at an Inlet

The DUS measured velocity waveform, $u_{in}\left(t\right)$, has been commonly used as the inflow BC [6] in ICHD. For a pipe with its radius of R, the typical way to introduce the pulsatile velocity to drive the flow into the pipe is to construct a parabolic profile of Poiseuille flow, $u\left(r,t\right)=u_{in}\left(r,t\right)\left(1-r^2/R^2\right)$, in which r is the distance to the pipe center. However, real arterial lumens are often not perfectly circular. To use this parabolic velocity profile, one needs to extend the inlet from noncircular to circular, which may introduce an unrealistic inflow.

We present an algorithm, as illustrated in Figure 3, for an irregular paraboloid-like velocity profile that fits the real inlet cross-section. The velocity waveform of $u_{in}\left(t\right)$ is digitized from the patient’s DUS shown in Figure 3a. It should be noted that, for a blood flow, the inflow velocity is pulsatile thus the irregular velocity profile needs to be constructed at every time point and the time resolution should be fine enough, determined through a temporal convergence check. To refine the temporal resolution, we use linear interpolation.

Assume the inlet plane is perpendicular to the z-direction, i.e., the direction of the bloodstream, and it is located at $z=z_0$. On the plane, each cell has known $\mathcal{P}\left(i,j,z_0\right)$ with $i=1,\dots ,N_x$ and $j=1,\dots ,N_y$. The algorithm to generate an irregular paraboloidal velocity profile at time t includes the following steps, schematized in Figure 3b.

(1)

Declare a matrix $N_x\times N_y$, i.e., $L_{ij}$ ($i=1,\dots ,N_x, j=1,\dots ,N_y$) and initialize it as $L_{ij}=0$.

(2)

Loop i from 1 to $N_x$ and j from 1 to $N_y$, if

• a cell’s $\mathcal{P}$ is neither 0 nor 1 (i.e., a boundary cell), assign $L_{ij}=0$ for this cell and define its velocity magnitude 0,
• a cell’s $\mathcal{P}$ is 0 (i.e., a fluid cell) and the $L_{ij}$ value of any neighboring cell is 0, assign $L_{ij}=1$ for this cell,
• a cell’s $\mathcal{P}$ is 0 and the $L_{ij}$ value of any neighboring cell is 1, assign $L_{ij}=2$ for this cell,
• continue until all the fluid cells are assigned. The last index of the cell labeling is $L_{ij}=M$.

(3)

Loop i from 1 to $N_x$ and j from 1 to $N_y$ and define velocity magnitude as $u_{ij}\left(t\right)=L_{ij}\times u_{in}\left(t\right)/M$.

The largest velocity $u_{in}\left(t\right)$ is recognized at the cell labeled as $L_{ij}=M$. The velocity reduces radially from $u_{in}\left(t\right)$ at label M (center) to zero at label $L_{ij}=0$ (wall). Figure 3c shows two views of paraboloid-like velocity distribution on an irregular inlet plane at a time point. The inlet velocity profile is introduced in VLBM through Equation (6).

2.1.3. WK3-Based Pressure BC at an Outlet

For the outlet BC, we use the popular WK3 model in an open vessel loop to calculate the pressure, $p\left(t\right)$, on the outlet plane. It has been well-known that WK3 is the best outlet BC model among other physiologically relevant zero-dimenensional outflow models to simulate the peripheral vasculature [37] and has been popularly used when significant compliance is located in the modeled distal vasculature [12]. As shown in Figure 4, WK3 is an analogy to an electrical circuit, which models the distal vasculature with one capacitor, modeling vessel compliance and two resistors, modeling proximal and distal resistance. The flow rate (Q) and the mean pressure ($p$) over the outlet plane are related by the following ordinary differential equation [12]

$$\frac{dp}{dt}+\frac{1}{RC}p=r\frac{dQ}{dt}+\frac{1}{RC}\left(r+R\right)Q$$

(8)

where r and R represent the proximal and distal resistances, and C is the compliance of the distal vasculature. Specifically, r is used to absorb the incoming waves and reduce artificial wave reflections. Equation (8) has an analytical solution.

$$p\left(t\right)=e^{-t/(RC)}{{\displaystyle \int }}_0^t{e}^{s/\left(RC\right)}\left[rdQ\left(s\right)/ds+\left(r+\frac{RQ\left(s\right)}{RC}\right)\right]ds+p_{t=0}$$

(9)

where $p_{t=0}$ is the initial pressure at the outlet.

In Equation (9), the three elements, r, C, and R, specified at each outlet, must be tuned to obtain the physiological values for the total outflow rate $Q_t$ and target systolic ($p_{sys}$) and diastolic ($p_{dia}$) pressure, with the mean arterial pressure, $p_m=\left(p_{sys}+2p_{dia}\right)/3$, based on patient’s clinical data. For an aortorenal system, see Figure 5 below, we use brachial pressure for a pressure target and DUS velocity waveform for the target flow rate (Q) with the understanding that the capacitor and resistors have independent functionalities in the WK3 circuit: a capacitor reflects the pulsatility of blood flow whereas a resistor determines the flow rate [15]

The integration of the WK3 model [15] and VLBM is described as follows

(1)

Determine the total resistance in the arterial segment

• Assume the total system compliance $C_t=0.1$ cm⁵/dynes.
• Calculate the total resistance $R_t\left(=r+R\right)=p_m/Q_t$.

(2)

Determine r and R at each outlet based on the published works: the proximal resistance r weights 28% [38,39] and 5.6% [40] out of the total resistance in the renal artery and abdominal aorta, respectively.

(3)

Tune r and R based on DUS flow rate at each outlet.

• Integrate the pressure BC from the WK3, Equation (9), into VLBM, Equation (7), and run InVascular. In one pulsation, r, R, and C remain the same but Q (t) at each outlet is obtained from the simulation.
• Once a simulation is done, check if the flow rate at each outlet matches that calculated from DUS imaging data. If yes, r and R are determined; If not, adjust R_t and repeat (1) b, (2), and (3).

(4)

Determine the compliance C at each outlet.

• Distribute $C_t$ to each outlet proportional to the corresponding mean flow rate.
• Check if the mean arterial pressure ${\overline{p}}_{in}^{CHD}$ matches ${\overline{p}}_{in}$ at the inlet. If not, adjust $C_t$ in (1) a. and repeat (1) and (2).

The outlet BC at each outlet is introduced in VLBM through Equations (4) and (7) after the pressure is obtained from Equation (9) at each time step.

2.2. Uncertainty Quantification

There is no doubt that uncertainty always exists in any modeling and simulation process [41]. In the process shown in the flowchart of InVascular in Figure 2, uncertainties come from noises introduced during image scanning and the extraction of the arterial segmentation, the use of empirical blood properties, parameters involved in the boundary conditions, and so on. The uncertainties in the input variables will affect the output (hemodynamics) of InVascular. Following the common practice in uncertainty quantification (UQ), we treat the parameters with uncertainty as random variables and quantify their effects on the output variables. In this study, we use the common UQ method: the First Order Second Moment (FOSM) [42] method.

Denote output variables by $\mathbf{Y}={\left(Y_1,Y_2,\dots ,Y_m\right)}^{\mathrm{T}}$ and input variables by $\mathbf{X}={\left(X_1,X_2,\dots ,X_n\right)}^{\mathrm{T}}$, where m and $n$ are the numbers of output and input variables, respectively. If the elements of $\mathbf{X}$ are non-normally distributed and dependent, Rosenblatt transformation [43] can be used to transform $\mathbf{X}$ into independent and normal variables.

Suppose the black-box models of InVascular are given by:

$$Y_j=g_j\left(\mathbf{X}\right), j=1,2,\dots ,m)$$

(10)

Linearizing a model at the mean values, $\mu =\left({\mu }_1,{\mu }_2,\dots ,{\mu }_n\right)$, of $\mathit{X}$, yields

$$Y_j\approx g_j\left(\mu \right)+{\nabla }^T\left(\mathbf{X}-\mu \right), j=1,2,\dots ,m$$

(11)

where $\nabla ={\left(\frac{\partial g}{\partial X_1},\frac{\partial g}{\partial X_2},\dots ,\frac{\partial g}{\partial X_n}\right)}^T$ is the gradient of $g_j\left(\mathbf{X}\right)$ at $\mu .$ Since $Y_j$ is approximated as a linear combination of $\mathit{x}$, it is also normally distributed, denoted by $N\left({\mu }_{Y_j},{\sigma }_{Y_j}^2\right)$ with ${\mu }_{Y_j}$ and ${\sigma }_{Y_j}$, the mean and standard deviation of $Y_j$, respectively. The two parameters are given as follows.

$${\mu }_{Y_j}=g_j\left(\mathbf{X}\right), j=1,2,\dots ,m$$

(12)

$${\sigma }_{Y_j}^2={\displaystyle \sum }_{i=1}^n{\left(\frac{\partial g_j}{\partial X_i}\right)}^2{\sigma }_i^2, j=1,2,\dots ,m$$

(13)

where ${\sigma }_i$ is the standard deviation of $X_i$. The covariance between output variables $Y_j$ and $Y_k$ is calculated by

$$C_{jk}={\displaystyle \sum }_{i=1}^n\left(\frac{\partial g_j}{\partial X_i}\right)\left(\frac{\partial g_k}{\partial X_i}\right){\sigma }_i^2$$

(14)

Then the joint probability density function (PDF) of output $Y={\left(Y_1,Y_2,\dots ,Y_m\right)}^T$ is determined by the mean vector ${\mu }_Y={\left({\mu }_{Y_1},{\mu }_{Y_2},\dots ,{\mu }_{Y_m}\right)}^T$ and covariance matrix ${\mathsf{\Sigma }}_Y={\left(C_{jk}\right)}_{j,k=1,2,\dots ,m}$. Since $g_j\left(\mathbf{X}\right)$ is a black box, its gradient is evaluated numerically by the finite difference method. The total computational cost, measured by the number of function (model) calls, is $n+1$. The efficiency is high since the number of function calls is linearly proportional to the dimensionality of input variables.

2.3. Materials

We studied six human aortorenal arterial systems. The medical data of each case included CTA images and DUS waveforms at the inlet and outlets, obtained from the electronic medical libraries in Indiana University Methodist Hospital in Indianapolis, Indiana, USA, and Hangzhou First People’s Hospital, Hangzhou, China. The CTA resolutions are approximately 0.752 × 2.5 mm³ (US cases) and 0.652 × 0.6mm³ (China cases).

We show one representative case in Figure 5 to demonstrate the integration of VLBM and physiological BCs at inlet and outlets, for InVascular. The aortorenal arterial system, anatomically extracted from the patient’s CTA data, consists of the aortic artery (AA), left renal artery (LRA), and right renal artery (RRA). The inlet BC based on the DUS velocity waveform and outlet BCs of WK3 are imposed at the inlet and three outlets, respectively. A minor lumen reduction (circled, about 20% lumen reduction) is seen in the LRA. The DUS images are available at the AA inlet to construct a paraboloidal velocity profile and outlets of AA, LRA, and RRA to tune the r, R, and C parameters. The physical flow domain is 63 × 116 × 84 mm³. The cardiac cycle is 0.68 s with a time resolution of 6.79 ms. The density and kinematic viscosity are 1.06 × 10³ kg/m³ and 3.3 × 10⁻⁶ m/s², respectively. The dimensionless relaxation time τ in VLBM is 0.5079.

The WK3 parameters r, R, and C at the three outlets are listed in

Table 1. Values of resistance and compliance parameters, r, R, and C, in WK3 model at corresponding outlets tuned from the DUS data.

Outlet	r (dynes×s/cm5)	R (dynes×s/cm5)	105C (cm5/dynes)
AA	88.0	2773.1	1.8
LRA	2982.4	7666.03	0.36
RRA	5972.8	15358.7	0.32

. The pulsatile pressure waveforms in AA, LRA, and RRA were invasively measured during a clinical intervention, which are used to validate the computed pressure below. As seen in Figure 6 below, for a given pressure waveform, the pressure values at the peak and the end of the waveform are called systolic blood pressure, $p_{sys}$, and diastolic blood pressure, $p_{dia}$, respectively. The mean arterial pressure (MAP) is defined as $MAP=\left(p_{sys}-p_{dia}\right)/3+p_{dia}$.

The spatial and temporal convergence checks are exhibited in

Table 2. Spatial (left) and temporal (right) convergence check. The spatial reoslution is represented by the grid number along the flow direction. MAP and $p_{sys}$ stand for mean arterial presure and systolic pressure, respectively. The relative error is the normalized difference of the correponding pressure values between two sucsessive grids and cycles.

Spatial			Temporal
Grid	MAP(mmHg)	Relative Error (%)	Cycle	${\mathit{P}}_{\mathit{s}\mathit{y}\mathit{s}} \left(\mathbf{mmHg}\right)$	Relative Error (%)
170	100		1	150
180	87.5	12.5	3	154	2.7
190	89	1.71	5	152	−1.3
200	90	0.34	10	155	2.0
210	90.15	0.19	15	155	0
220	90.20	0.05	20	155	0

. The relative errors are the normalized differences of the mean arterial pressure (MAP) and systolic pressure ($P_{sys}$) between two successive grids and cycles, respectively. To balance the accuracy and the computation cost, we chose 200 × 368 × 265 as the resolution for the simulation and run 10 cycles to produce the computational results.

3. Results

In this section, we demonstrate the applicability and reliability of InVascular in two aspects. First, we use the representative study case to show the computed pulsatile pressure, velocity, and vorticity fields in the arterial system. The noninvasively computed pressure waveforms are compared with the invasively measured ones at three locations. Second, we perform a systematic UQ analysis for the representative case and for all six cases to study how the r, R, and C parameters impact the computed pressure.

3.1. Pulsatile Hemodynamics in an Aortorenal Arterial System

We first demonstrate the accuracy of InVascular for the quantification of the pulsatile pressure field. Figure 6 shows the comparisons of the cyclic pressure waveforms in (a) AA, (b) RRA, and (c) LRA between noninvasive computation (solid lines) and invasive measurements (dashed lines).

The computed pressure waveforms agree very well with the medical measured waveforms. The pressure contours on (a) the AA-LRA plane, (b)AA-RRA plane, and (c) representative cross-sections are plotted in Figure 7. The trans-stenotic pressure gradient ($TSPG$) in the LRA can be calculated through ether $MAP$ or $p_{sys}.$ The comparison of the TSPGs between noninvasive computation and invasive measurement is shown in

Table 3. Comparison of TSPG in LRA and RRA based on MAP $and{p}_{sys}$.

$\mathit{T}\mathit{S}\mathit{P}\mathit{G}$	$\mathit{M}\mathit{A}\mathit{P}$		${\mathit{p}}_{\mathit{s}\mathit{y}\mathit{s}}$
	Computed	Measured	Computed	Measured
$p_a-p_r$, left	2.5	2.6	4.1	4.0
$p_a-p_r$, right	2.0	2.0	4.0	4.0

. Again, both are in good agreement.

We found that the fully-developed BC and DUS-based velocity BC, which are commonly used in the LBM, cannot capture the physiological pressure waveform. Figure 8 shows the cyclic evolution of the systolic pressure at a representative location in the arterial system under three different BCs with identical computation environments and conditions. Neither the fully-developed BC (long dash) nor DUS-based velocity BC (short dash) is convergent. The pressure (left scale) asymptotically increases with time and exceeds the human blood pressure after a few cardiac cycles, whereas the WK3-based pressure BC (solid line) leads to a convergent systolic pressure ($p_{sys}\approx 154.8 \mathrm{mmHg}$) (right vertical scale) after 10 cardiac cycles.

Besides the pressure field, InVascular simultaneously computes the pulsatile velocity field, from which the vorticity and shear stress fields can be calculated. Figure 9 and Figure 10 show the velocity field with magnitude contours and streamlines and vorticity contours, respectively, at t = (a) 0.1, (b) 0.23, and (c) 0.63 in seconds in one cardiac cycle corresponding to systole (heart contraction, flow acceleration), diastole (heart relaxation, flow deceleration), and the end of diastole respectively. In Figure 9, flow in AA is stronger at systole (a) than at diastole (b) but remains intensive in LRA and RRA at both time points and is better organized at systole than at diastole. Whereas at the end of diastole, the flow is weak but chaotic. The vorticity contours shown in Figure 10 are similarly intensive in (a) and (b) with a large degree of skewness in AA, demonstrating the complexity of the flow in the real arteries. At the end of diastole, vorticity contours are much smaller and chaotic.

3.2. Impact of r, C, and R Parameters on Pressure Quantification

Although the WK3 has been popularly used to model the physiological BC at each outlet of the artery segment (see Figure 5), its parameters reflecting resistances, r and R, and compliance, C, are determined empirically [38,39,40], which is subjected to uncertainty. To demonstrate the impact of the uncertainty in r-C-R parameters on the quantification of proximal and distal pressure, we performed a UQ analysis using FOSM. The input variables are the r, R, and C parameters in WK3, defined in

Table 4. Input distributions for the representative case in Section 3.1.

Artery	Parameter	Variables	Mean	Standard Deviation	Distribution Type
AA	r(dynes×s/cm5)	$X_1$	108.12	3.24	Normal
AA	R(dynes×s/cm5)	$X_2$	3386.38	101.59	Normal
LRA	r(dynes×s/cm5)	$X_3$	2879.76	86.39	Normal
LRA	R(dynes×s/cm5)	$X_4$	7386.06	221.58	Normal
RRA	r(dynes×s/cm5)	$X_5$	3306.39	99.19	Normal
RRA	R(dynes×s/cm5)	$X_6$	8505.96	255.18	Normal
AA	C(cm5/dynes)	$X_7$	$1.0\times {10}^{-5}$	$3.0\times {10}^{-7}$	Normal
LRA	C(cm5/dynes)	$X_8$	$5.4\times {10}^{-6}$	$1.62\times {10}^{-7}$	Normal
RRA	C(cm5/dynes)	$X_9$	$4.8\times {10}^{-6}$	$1.43\times {10}^{-7}$	Normal

. The elements of $\mathbf{X}$ are independently and normally distributed. The output variables are the pressure values in AA, LRA, and RRA, defined in

Table 5. UQ results.

Artery	Output Variable	$\mathbf{Mean} {\mathit{\mu }}_{{\mathit{y}}_1}$	$\mathbf{Standard} \mathbf{Deviation} {\mathit{\sigma }}_{{\mathit{y}}_1}$	95% Confidence Interval
AA	$Y_1$ (mmHg)	155.80	1.37	[153.05, 158.55]
LRA	$Y_2$ (mmHg)	141.72	1.12	[139.49, 143.95]
RRA	$Y_3$ (mmHg)	144.61	1.12	[142.37, 147.86]

. In this study, we assumed that the standard deviation of a random input variable is 3% of its mean. We performed UQ for five cases. The input distributions for the representative case in Section 3.1 are shown in Table 4.

UQ results are given in Table 5. All the model output variables are normally distributed. For example, $Y_1~N\left({\mu }_{Y_1},{\sigma }_{Y_1}\right)=N\left(155.80 \mathrm{mmHg},1.37\right)$. With these results, we know complete information about the simulation predictions, including the 95% confidence intervals of the model predictions. The formula for 95% confidence interval is ${\mu }_{Y_i} \pm$2${\sigma }_{Y_i}$. For example, the 95% confidence interval of $Y_1$ is [153.051, 158.55] mmHg unit. This means that the chance the actual value of $Y_1$ falling into the interval is 95%, or we have 95% confidence that the actual value of $Y_1$ is between 153.05 mmHg and 158.56 mmHg. The results of mean and standard deviation from five patients are also given in

Table 6. Mean and standard deviation of five patient cases.

Case	${\mathit{Y}}_1 \left(\mathbf{mmHg}\right)$	${\mathit{Y}}_2 \left(\mathbf{mmHg}\right)$	${\mathit{Y}}_3 \left(\mathbf{mmHg}\right)$
1	$N\left(156.80,{1.37}^2\right)$	$N\left(141.72,{1.11}^2\right)$	$N\left(144.61,{1.12}^2\right)$
2	$N\left(163.61,{2.06}^2\right)$	$N\left(154.25,{1.93}^2\right)$	$N\left(56.42,{0.09}^2\right)$
3	$N\left(157.22,{1.54}^2\right)$	$N\left(152.35,{1.45}^2\right)$	$N\left(153.85,{1.47}^2\right)$
4	$N\left(109.71,{0.93}^2\right)$	$N\left(106.49,{0.89}^2\right)$	$N\left(74.50,{0.56}^2\right)$
5	$N\left(123.21,{0.97}^2\right)$	$N\left(117.34,{0.89}^2\right)$	$N\left(102.17,{1.24}^2\right)$

. The 95% confidence intervals of the model predictions of five patients are in

Table 7. 95% confidence intervals of model predictions of five patient cases.

Case	${\mathit{Y}}_1 \left(\mathbf{mmHg}\right)$	${\mathit{Y}}_2 \left(\mathbf{mmHg}\right)$	${\mathit{Y}}_3 \left(\mathbf{mmHg}\right)$
1	[153.05, 158.55]	[139.49, 143.95]	[142.37, 146.86]
2	[159.48, 167.74]	[150.38, 158.12]	[56.25, 56.59]
3	[154.14, 160.30]	[149.45,155.25]	[150.92,156.79]
4	[107.84, 111.58]	[104.72,108.27]	[73.37,75.62]
5	[121.28, 125.15]	[115.57, 119.11]	[99.69,104.64]

.

4. Discussion

We have presented the physiological inlet and outlet BCs for ICHD and integrated them into our in-house computational platform, InVascular. Using the unified LBM modeling for image segmentation and computational hemodynamics, InVascular seamlessly integrates the anatomical extraction of the interested arterial segment and quantification of pulsatile hemodynamics and achieves fast computation via GPU parallel computing. The inlet BC is a pulsatile velocity. A paraboloidal velocity profile is constructed based on the DUS velocity waveform, which fits the real shape of the arterial lumen (usually noncircular). Each outlet BC is a pulsatile pressure determined by WK3 during the simulation. The inlet velocity and outlet pressure BCs are introduced in the VLBM via a non-equilibrium extrapolation BC scheme. Using InVascular, we performed UQ analysis to quantify the impact of input variations caused by uncertainties. We applied InVascular into a human aortorenal arterial system extracted from medical CTA imaging data and demonstrated the applicability and reliability of InVascular for a real-world flow system. Six cases were studied. The pressure waveforms in AA, LRA, and RRA computed from InVascular have excellent agreements with the invasive measurements. The pulsatile velocity and then vorticity fields are shown as well. Due to the lack of available data, the validation of the velocity quantification has not been conducted. A systematic UQ analysis focuses on the impact of the variation of r, R, and C parameters on the quantification of the pressure field. Results include joint probability density of the computed pressure, which also provides the uncertainty or the confidence of the prediction. Due to the suitability of LBM for GPU parallel computing, InVascular features exceptionally fast computation speed. With a great potential to further speed up through parallel optimization and/or multiple GPU cards, the computation time is expected to be around 10 min per patient case. Such a computation capability is critically important for the clinical use of InVascular, enabling massive numerical analysis through parametrization to assess the true degree of existing arterial stenosis, either severe for immediate therapeutics or mild to avoid unnecessary intervention, within clinic permitted time.