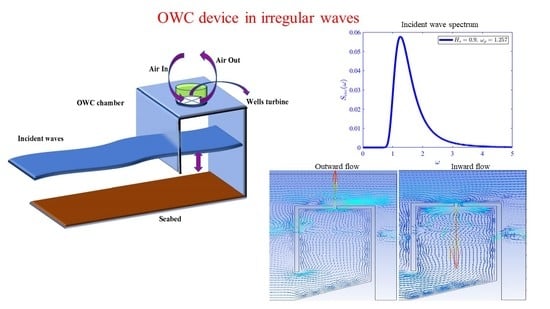
Hydrodynamics of an OWC Device in Irregular Incident Waves Using RANS Model
Abstract
:1. Introduction
2. Modeling of the Numerical Wave Tank (NWT)
2.1. Geometry and Grid Generation
2.2. Governing Equations
2.3. Boundary Conditions and Generation of Free Surface
3. Hydrodynamic Performance of the OWC Device in an Irregular-Wave Environment
4. Results
4.1. Comparison with the Existing Results
4.2. Grid-Convergence Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Norouzi, N.; Fani, M. Black gold falls, black plague arise-An Opec crude oil price forecast using a gray prediction model. Upstream Oil Gas Technol. 2020, 5, 100015. [Google Scholar] [CrossRef]
- Altunkaynak, A.; Çelik, A. A novel Geno-fuzzy based model for hydrodynamic efficiency prediction of a land-fixed oscillating water column for various front wall openings, power take-off dampings and incident wave steepnesses. Renew. Energy 2022, 196, 99–110. [Google Scholar] [CrossRef]
- Shahzad, U. The need for renewable energy sources. Energy 2012, 2, 16–18. [Google Scholar]
- Kharati-Koopaee, M.; Fathi-Kelestani, A. Assessment of oscillating water column performance: Influence of wave steepness at various chamber lengths and bottom slopes. Renew. Energy 2020, 147, 1595–1608. [Google Scholar] [CrossRef]
- Heath, T.V. A review of oscillating water columns. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2012, 370, 235–245. [Google Scholar] [CrossRef] [Green Version]
- Koley, S.; Trivedi, K. Mathematical modeling of oscillating water column wave energy converter devices over the undulated sea bed. Eng. Anal. Bound. Elem. 2020, 117, 26–40. [Google Scholar] [CrossRef]
- Evans, D.V. The oscillating water column wave-energy device. IMA J. Appl. Math. 1978, 22, 423–433. [Google Scholar] [CrossRef]
- Evans, D.V. Wave-power absorption by systems of oscillating surface pressure distributions. IMA J. Fluid Mech. 1982, 114, 481–499. [Google Scholar] [CrossRef]
- Sarmento, A.J.; Falcão, A.D.O. Wave generation by an oscillating surface-pressure and its application in wave-energy extraction. J. Fluid Mech. 1985, 150, 467–485. [Google Scholar] [CrossRef]
- Evans, D.V.; Porter, R. Hydrodynamic characteristics of an oscillating water column device. Appl. Ocean. Res. 1995, 17, 155–164. [Google Scholar] [CrossRef]
- De O Falcão, A.F.; Rodrigues, R.J.A. Stochastic modelling of OWC wave power plant performance. Appl. Ocean. Res. 2002, 24, 59–71. [Google Scholar] [CrossRef]
- Falcão, A.F.; Henriques, J.C.; Gato, L.M.; Gomes, R.P. Air turbine choice and optimization for floating oscillating-water-column wave energy converter. Ocean. Eng. 2014, 75, 148–156. [Google Scholar] [CrossRef]
- Rezanejad, K.; Soares, C.G.; López, I.; Carballo, R. Experimental and numerical investigation of the hydrodynamic performance of an oscillating water column wave energy converter. Renew. Energy 2017, 106, 1–16. [Google Scholar] [CrossRef]
- Iturrioz, A.; Guanche, R.; Armesto, J.A.; Alves, M.A.; Vidal, C.; Losada, I.J. Time-domain modeling of a fixed detached oscillating water column towards a floating multi-chamber device. Ocean. Eng. 2014, 76, 65–74. [Google Scholar] [CrossRef]
- Zheng, S.; Zhang, Y.; Iglesias, G. Coast/breakwater-integrated OWC: A theoretical model. Mar. Struct. 2019, 66, 121–135. [Google Scholar] [CrossRef]
- Ning, D.Z.; Guo, B.M.; Wang, R.Q.; Vyzikas, T.; Greaves, D. Geometrical investigation of a U-shaped oscillating water column wave energy device. Appl. Ocean. Res. 2020, 97, 102105. [Google Scholar] [CrossRef]
- Trivedi, K.; Koley, S. Mathematical modeling of breakwater-integrated oscillating water column wave energy converter devices under irregular incident waves. Renew. Energy 2021, 178, 403–419. [Google Scholar] [CrossRef]
- Ning, D.Z.; Shi, J.; Zou, Q.P.; Teng, B. Investigation of hydrodynamic performance of an OWC (oscillating water column) wave energy device using a fully nonlinear HOBEM (higher-order boundary element method). Energy 2015, 83, 177–188. [Google Scholar] [CrossRef]
- Rodríguez, A.A.M.; Casarín, R.S.; Ilzarbe, J.M.B. A 3D boundary element method for analysing the hydrodynamic performance of a land-fixed oscillating water column device. Eng. Anal. Bound. Elem. 2022, 138, 407–422. [Google Scholar] [CrossRef]
- Falnes, J. Ocean Waves and Oscillating Systems: Linear Interactions Including Wave-Energy Extraction; Cambridge University Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- López, I.; Pereiras, B.; Castro, F.; Iglesias, G. Optimisation of turbine-induced damping for an OWC wave energy converter using a RANS–VOF numerical model. Appl. Energy 2014, 127, 105–114. [Google Scholar] [CrossRef]
- Luo, Y.; Nader, J.R.; Cooper, P.; Zhu, S.P. Nonlinear 2D analysis of the efficiency of fixed oscillating water column wave energy converters. Renew. Energy 2014, 64, 255–265. [Google Scholar] [CrossRef]
- Simonetti, I.; Cappietti, L.; Elsafti, H.; Oumeraci, H. Evaluation of air compressibility effects on the performance of fixed OWC wave energy converters using CFD modelling. Renew. Energy 2018, 119, 741–753. [Google Scholar] [CrossRef]
- Wang, R.Q.; Ning, D.Z.; Zhang, C.W.; Zou, Q.P.; Liu, Z. Nonlinear and viscous effects on the hydrodynamic performance of a fixed OWC wave energy converter. Coast. Eng. 2018, 139, 42–50. [Google Scholar] [CrossRef]
- Dai, S.; Day, S.; Yuan, Z.; Wang, H. Investigation on the hydrodynamic scaling effect of an OWC type wave energy device using experiment and CFD simulation. Renew. Energy 2019, 142, 184–194. [Google Scholar] [CrossRef]
- Gurnari, L.; Filianoti, P.G.; Torresi, M.; Camporeale, S.M. The wave-to-wire energy conversion process for a fixed U-OWC Device. Energies 2020, 13, 283. [Google Scholar] [CrossRef] [Green Version]
- Vyzikas, T.; Deshoulières, S.; Giroux, O.; Barton, M.; Greaves, D. Numerical study of fixed Oscillating Water Column with RANS-type two-phase CFD model. Renew. Energy 2017, 102, 294–305. [Google Scholar] [CrossRef] [Green Version]
- Da Silva Koch, A.H.; Da Silveira Paiva, M.; Monteiro, C.B.; Oleinik, P.H.; Isoldi, L.A.; Machado, B.N. Numerical Evaluation of the Hydropneumatic Power of the Oscillating Water Column Wave Energy Converter Submitted to Regular and Irregular Waves. Eng. Sci. Technol. 2022, 3, 32–43. [Google Scholar] [CrossRef]
- Zhou, Z.; Ke, S.; Wang, R.; Mayon, R.; Ning, D. Hydrodynamic Investigation on a Land-Fixed OWC Wave Energy Device under Irregular Waves. Appl. Sci. 2022, 12, 2855. [Google Scholar] [CrossRef]
- Mohapatra, P.; Bhattacharyya, A.; Sahoo, T. Performance of a floating oscillating water column wave energy converter over a sloping bed. Ships Offshore Struct. 2021, 16, 659–669. [Google Scholar] [CrossRef]
- Mohapatra, P.; Vijay, K.G.; Bhattacharyya, A.; Sahoo, T. Performance of a shore fixed oscillating water column device for different bottom slopes and front wall drafts: A study based on computational fluid dynamics and biem. J. Offshore Mech. Arct. Eng. 2021, 143, 032002. [Google Scholar] [CrossRef]
- Liu, S.; Ong, M.C.; Obhrai, C.; Gatin, I.; Vukčević, V. Influences of free surface jump conditions and different k-ω SST turbulence models on breaking wave modelling. Ocean. Eng. 2020, 217, 107746. [Google Scholar] [CrossRef]
- Menter, F.R. Improved Two-Equation k-ω Turbulence Models for Aerodynamic Flows; No. A-92183; NASA Ames Research Center: Moffett Field, CA, USA, 1992. [Google Scholar]
- Wilcox, D.C. Formulation of the kw turbulence model revisited. AIAA J. 2008, 46, 2823–2838. [Google Scholar] [CrossRef] [Green Version]
- Xu, C.; Huang, Z. Three-dimensional CFD simulation of a circular OWC with a nonlinear power-takeoff: Model validation and a discussion on resonant sloshing inside the pneumatic chamber. Ocean. Eng. 2019, 176, 184–198. [Google Scholar] [CrossRef]
- Gomes, M.D.N.; Olinto, C.R.; Isoldi, L.A.; Souza, J.A.; Rocha, L.A.D.O. Computational Modeling of the Air-Flow in an Oscillating Water Column System. 2009. Available online: http://repositorio.furg.br/handle/1/4999 (accessed on 24 October 2022).
- Gomes, R.P.F.; Henriques, J.C.C.; Gato, L.M.C.; Falcão, A.D.O. Hydrodynamic optimization of an axisymmetric floating oscillating water column for wave energy conversion. Renew. Energy 2012, 44, 328–339. [Google Scholar] [CrossRef]
- Rezanejad, K.; Gadelho, J.F.M.; Guedes Soares, C. Hydrodynamic analysis of an oscillating water column wave energy converter in the stepped bottom condition using CFD. Renew. Energy 2019, 135, 1241–1259. [Google Scholar] [CrossRef]
- Ning, D.Z.; Wang, R.Q.; Gou, Y.; Zhao, M.; Teng, B. Numerical and experimental investigation of wave dynamics on a land-fixed OWC device. Energy 2016, 115, 326–337. [Google Scholar] [CrossRef]
































| Pressure Drop | Flow Rate q | Free Surface Elevation y | |
|---|---|---|---|
| p | |||
| (m) | (Hz) | (kW/m) | (kW/m) | ||
|---|---|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trivedi, K.; Ray, A.R.; Krishnan, P.A.; Koley, S.; Sahoo, T. Hydrodynamics of an OWC Device in Irregular Incident Waves Using RANS Model. Fluids 2023, 8, 27. https://doi.org/10.3390/fluids8010027
Trivedi K, Ray AR, Krishnan PA, Koley S, Sahoo T. Hydrodynamics of an OWC Device in Irregular Incident Waves Using RANS Model. Fluids. 2023; 8(1):27. https://doi.org/10.3390/fluids8010027
Chicago/Turabian StyleTrivedi, Kshma, Amya Ranjan Ray, Parothidil Anjusree Krishnan, Santanu Koley, and Trilochan Sahoo. 2023. "Hydrodynamics of an OWC Device in Irregular Incident Waves Using RANS Model" Fluids 8, no. 1: 27. https://doi.org/10.3390/fluids8010027
APA StyleTrivedi, K., Ray, A. R., Krishnan, P. A., Koley, S., & Sahoo, T. (2023). Hydrodynamics of an OWC Device in Irregular Incident Waves Using RANS Model. Fluids, 8(1), 27. https://doi.org/10.3390/fluids8010027