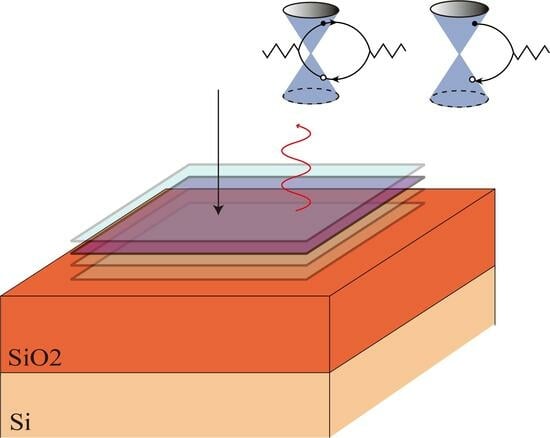
Introducing Corrections to the Reflectance of Graphene by Light Emission
Abstract
:1. Introduction
2. Reflectance of Graphene Multilayer on Si Substrate
2.1. Fresnel Equation
2.2. Comparison of Measured and Calculated Contrasts
2.3. Effective Coupling Constant
3. Corrections to Reflectance by Light Emission
3.1. Basic Idea
3.2. Primary Model
3.3. Model of Light Emission

4. Applications of Model
4.1. Comparison of Theory and Experiment
4.2. Monolayer
4.3. Raman Scattering as Incoherent Corrections
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Measured Reflectivities

References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef]
- Zhang, Y.; Tan, Y.W.; Stormer, H.L.; Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 2005, 438, 201–204. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Jiang, D.; Schedin, F.; Booth, T.J.; Khotkevich, V.V.; Morozov, S.V.; Geim, A.K. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. USA 2005, 102, 10451–10453. [Google Scholar] [CrossRef]
- Blake, P.; Hill, E.W.; Neto, A.H.C.; Novoselov, K.S.; Jiang, D.; Yang, R.; Booth, T.J.; Geim, A.K. Making graphene visible. Appl. Phys. Lett. 2007, 91, 063124. [Google Scholar] [CrossRef]
- Roddaro, S.; Pingue, P.; Piazza, V.; Pellegrini, V.; Beltram, F. The optical visibility of graphene: Interference colors of ultrathin graphite on SiO2. Nano Lett. 2007, 7, 2707–2710. [Google Scholar] [CrossRef]
- Ni, Z.H.; Wang, H.M.; Kasim, J.; Fan, H.M.; Yu, T.; Wu, Y.H.; Feng, Y.P.; Shen, Z.X. Graphene Thickness Determination Using Reflection and Contrast Spectroscopy. Nano Lett. 2007, 7, 2758–2763. [Google Scholar] [CrossRef] [PubMed]
- Casiraghi, C.; Hartschuh, A.; Lidorikis, E.; Qian, H.; Harutyunyan, H.; Gokus, T.; Novoselov, K.S.; Ferrari, A.C. Rayleigh Imaging of Graphene and Graphene Layers. Nano Lett. 2007, 7, 2711–2717. [Google Scholar] [CrossRef]
- Ghamsari, B.G.; Tosado, J.; Yamamoto, M.; Fuhrer, M.S.; Anlage, S.M. Measuring the Complex Optical Conductivity of Graphene by Fabry-Pérot Reflectance Spectroscopy. Sci. Rep. 2016, 6, 34166. [Google Scholar] [CrossRef]
- Nemanich, R.J.; Tsai, C.C.; Connell, G.A.N. Interference-Enhanced Raman Scattering of Very Thin Titanium and Titanium Oxide Films. Phys. Rev. Lett. 1980, 44, 273–276. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Ni, Z.H.; Shen, Z.X.; Wang, H.M.; Wu, Y.H. Interference enhancement of Raman signal of graphene. Appl. Phys. Lett. 2008, 92, 043121. [Google Scholar] [CrossRef]
- Stöhr, R.J.; Kolesov, R.; Pflaum, J.; Wrachtrup, J. Fluorescence of laser-created electron-hole plasma in graphene. Phys. Rev. B 2010, 82, 121408. [Google Scholar] [CrossRef]
- Lui, C.H.; Mak, K.F.; Shan, J.; Heinz, T.F. Ultrafast photoluminescence from graphene. Phys. Rev. Lett. 2010, 105, 127404. [Google Scholar] [CrossRef]
- Liu, W.T.; Wu, S.W.; Schuck, P.J.; Salmeron, M.; Shen, Y.R.; Wang, F. Nonlinear broadband photoluminescence of graphene induced by femtosecond laser irradiation. Phys. Rev. B 2010, 82, 081408. [Google Scholar] [CrossRef]
- Suemoto, T.; Sakaki, S.; Nakajima, M.; Ishida, Y.; Shin, S. Access to hole dynamics in graphite by femtosecond luminescence and photoemission spectroscopy. Phys. Rev. B Condens. Matter Mater. Phys. 2013, 87, 224302. [Google Scholar] [CrossRef]
- Riaz, A.; Pyatkov, F.; Alam, A.; Dehm, S.; Felten, A.; Chakravadhanula, V.S.; Flavel, B.S.; Kübel, C.; Lemmer, U.; Krupke, R. Light emission, light detection and strain sensing with nanocrystalline graphene. Nanotechnology 2015, 26, 325202. [Google Scholar] [CrossRef]
- Song, J.C.; Tielrooij, K.J.; Koppens, F.H.; Levitov, L.S. Photoexcited carrier dynamics and impact-excitation cascade in graphene. Phys. Rev. B Condens. Matter Mater. Phys. 2013, 87, 155429. [Google Scholar] [CrossRef]
- Massicotte, M.; Soavi, G.; Principi, A.; Tielrooij, K.J. Hot carriers in graphene-fundamentals and applications. Nanoscale 2021, 13, 8376–8411. [Google Scholar] [CrossRef]
- Castriota, M.; Politano, G.G.; Vena, C.; De Santo, M.P.; Desiderio, G.; Davoli, M.; Cazzanelli, E.; Versace, C. Variable Angle Spectroscopic Ellipsometry investigation of CVD-grown monolayer graphene. Appl. Surf. Sci. 2019, 467–468, 213–220. [Google Scholar] [CrossRef]
- El-Sayed, M.A.; Ermolaev, G.A.; Voronin, K.V.; Romanov, R.I.; Tselikov, G.I.; Yakubovsky, D.I.; Doroshina, N.V.; Nemtsov, A.B.; Solovey, V.R.; Voronov, A.A.; et al. Optical Constants of Chemical Vapor Deposited Graphene for Photonic Applications. Nanomaterials 2021, 11, 1230. [Google Scholar] [CrossRef]
- Devang, P.; Simone, D.; Naga, A.P.; Kumar, S.; Ralph, K. Enhanced Broadband Photodetection with Geometry and Interface Engineered Nanocrystalline Graphite. Adv. Sensor Res. 2023, 2023, 2300134. [Google Scholar] [CrossRef]
- Sasaki, K.; Hitachi, K. Universal layer number in graphite. Commun. Phys. 2020, 3, 90. [Google Scholar] [CrossRef]
- Hendry, E.; Hale, P.J.; Moger, J.; Savchenko, A.K.; Mikhailov, S.A. Coherent nonlinear optical response of graphene. Phys. Rev. Lett. 2010, 105, 097401. [Google Scholar] [CrossRef]
- Sun, Z.; Hasan, T.; Torrisi, F.; Popa, D.; Privitera, G.; Wang, F.; Bonaccorso, F.; Basko, D.M.; Ferrari, A.C. Graphene mode-locked ultrafast laser. ACS Nano 2010, 4, 803–810. [Google Scholar] [CrossRef] [PubMed]
- Mikhailov, S.A. Theory of the nonlinear optical frequency mixing effect in graphene. Phys. E Low Dimens. Syst. Nanostruct. 2012, 44, 924–927. [Google Scholar] [CrossRef]
- Yang, H.; Guan, H.; Biekert, N.; Arefe, G.; Chang, D.C.; Sun, Y.; Yeh, P.C.; Liu, X.; Hong, S.Y.; Marion, I.D.; et al. Layer dependence of third-harmonic generation in thick multilayer graphene. Phys. Rev. Mater. 2018, 2, 071002. [Google Scholar] [CrossRef]
- Stauber, T.; Peres, N.M.R.; Geim, A.K. Optical conductivity of graphene in the visible region of the spectrum. Phys. Rev. B 2008, 78, 085432. [Google Scholar] [CrossRef]
- Stauber, T.; Parida, P.; Trushin, M.; Ulybyshev, M.V.; Boyda, D.L.; Schliemann, J. Interacting Electrons in Graphene: Fermi Velocity Renormalization and Optical Response. Phys. Rev. Lett. 2017, 118, 266801. [Google Scholar] [CrossRef]
- Aspnes, D.E.; Studna, A.A. Dielectric functions and optical parameters of Si, Ge, GaP, GaAs, GaSb, InP, InAs, and InSb from 1.5 to 6.0 eV. Phys. Rev. B 1983, 27, 985. [Google Scholar] [CrossRef]
- Malitson, I.H. Interspecimen Comparison of the Refractive Index of Fused Silica. J. Opt. Soc. Am. 1965, 55, 1205–1209. [Google Scholar] [CrossRef]
- Anders, H. Thin Films in Optics; The Focal Press: Waltham, MA, USA, 1965. [Google Scholar]
- Ando, T.; Zheng, Y.; Suzuura, H. Dynamical Conductivity and Zero-Mode Anomaly in Honeycomb Lattices. J. Phys. Soc. Jpn. 2002, 71, 1318–1324. [Google Scholar] [CrossRef]
- Nair, R.R.; Blake, P.; Grigorenko, A.N.; Novoselov, K.S.; Booth, T.J.; Stauber, T.; Peres, N.M.R.; Geim, A.K. Fine Structure Constant Defines Visual Transparency of Graphene. Science 2008, 320, 1308. [Google Scholar] [CrossRef]
- Kuzmenko, A.B.; van Heumen, E.; Carbone, F.; van der Marel, D. Universal Optical Conductance of Graphite. Phys. Rev. Lett. 2008, 100, 117401. [Google Scholar] [CrossRef]
- Sasaki, K.i. Layered Dynamical Conductivity for a Transfer Matrix Method —Application to an N-layer Graphene—. J. Phys. Soc. Jpn. 2020, 89, 094706. [Google Scholar] [CrossRef]
- Taft, E.A.; Philipp, H.R. Optical Properties of Graphite. Phys. Rev. 1965, 138, A197–A202. [Google Scholar] [CrossRef]
- Ichikawa, Y.H.; Kobayashi, K. Optical properties of graphite in the infrared region. Carbon 1966, 3, 401–406. [Google Scholar] [CrossRef]
- Dresselhaus, M.S.; Dresselhaus, G. Interpretation of infrared modulation spectroscopy data in graphite by the Slonczewski-Weiss- McClure band model. Phys. Rev. B 1976, 13, 4635–4636. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M.; Petrov, V.M. Impact of chemical potential on the reflectance of graphene in the infrared and microwave domains. Phys. Rev. A 2018, 98, 023809. [Google Scholar] [CrossRef]
- Fang, J.; Vandenberghe, W.G.; Fischetti, M.V. Microscopic dielectric permittivities of graphene nanoribbons and graphene. Phys. Rev. B 2016, 94, 045318. [Google Scholar] [CrossRef]
- Rickhaus, P.; Liu, M.H.; Kurpas, M.; Kurzmann, A.; Lee, Y.; Overweg, H.; Eich, M.; Pisoni, R.; Taniguchi, T.; Watanabe, K.; et al. The electronic thickness of graphene. Sci. Adv. 2020, 6, eaay8409. [Google Scholar] [CrossRef]
- Bruna, M.; Borini, S. Optical constants of graphene layers in the visible range. Appl. Phys. Lett. 2009, 94, 031901. [Google Scholar] [CrossRef]
- Djurišić, A.B.; Li, E.H. Optical properties of graphite. J. Appl. Phys. 1999, 85, 7404–7410. [Google Scholar] [CrossRef]
- Kuramoto, Y. Chemical Oscillations, Waves, and Turbulence; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar] [CrossRef]
- Velson, N.V.; Velson, N.V.; Zobeiri, H.; Wang, X.; Wang, X. Rigorous prediction of Raman intensity from multi-layer films. Opt. Express 2020, 28, 35272–35283. [Google Scholar] [CrossRef]
- Yoon, D.; Moon, H.; Cheong, H.; Choi, J.S.; Choi, J.A.; Park, B.H. Variations in the Raman Spectrum as a Function of the Number of Graphene Layers. J. Korean Phys. Soc. 2009, 55, 1299–1303. [Google Scholar] [CrossRef]
- Li, X.L.; Qiao, X.F.; Han, W.P.; Lu, Y.; Tan, Q.H.; Liu, X.L.; Tan, P.H. Layer number identification of intrinsic and defective multilayered graphenes up to 100 layers by the Raman mode intensity from substrates. Nanoscale 2015, 7, 8135–8141. [Google Scholar] [CrossRef]
- No, Y.S.; Choi, H.K.; Kim, J.S.; Kim, H.; Yu, Y.J.; Choi, C.G.; Choi, J.S. Layer number identification of CVD-grown multilayer graphene using Si peak analysis. Sci. Rep. 2018, 8, 571. [Google Scholar] [CrossRef]
- Dicke, R.H. Coherence in Spontaneous Radiation Processes. Phys. Rev. 1954, 93, 99. [Google Scholar] [CrossRef]
- Toqeer, I.; Yaqoob, M.Z.; Ghaffar, A.; Alkanhal, M.A.S.; Khan, Y.; Aladadi, Y.T. Reflectance and transmittance of terahertz waves from graphene embedded into metamaterial structures. J. Opt. Soc. Am. A 2021, 38, 465–475. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sasaki, K.-i.; Hitachi, K.; Kamada, M.; Yokosawa, T.; Ochi, T.; Matsui, T. Introducing Corrections to the Reflectance of Graphene by Light Emission. C 2024, 10, 18. https://doi.org/10.3390/c10010018
Sasaki K-i, Hitachi K, Kamada M, Yokosawa T, Ochi T, Matsui T. Introducing Corrections to the Reflectance of Graphene by Light Emission. C. 2024; 10(1):18. https://doi.org/10.3390/c10010018
Chicago/Turabian StyleSasaki, Ken-ichi, Kenichi Hitachi, Masahiro Kamada, Takamoto Yokosawa, Taisuke Ochi, and Tomohiro Matsui. 2024. "Introducing Corrections to the Reflectance of Graphene by Light Emission" C 10, no. 1: 18. https://doi.org/10.3390/c10010018
APA StyleSasaki, K. -i., Hitachi, K., Kamada, M., Yokosawa, T., Ochi, T., & Matsui, T. (2024). Introducing Corrections to the Reflectance of Graphene by Light Emission. C, 10(1), 18. https://doi.org/10.3390/c10010018