1. Introduction
Elastomers that consists of polymeric chains with a high degree of flexibility and mobility, exhibit rubber-like elasticity if the chains are joined into a network structure [
1]. They can undergo large deformations and they have very good damping characteristics making them well suited in energy dissipation. Rubberlike materials find applications in many sectors ranging from automobile tyres and conveyor belts, hoses, adhesives, aircraft industry, etc. The rubberlike elasticity is observed above the glass transition temperature T
g and above the melting point, T
m for crystalline polymers. Natural rubber undergoes strain-induced crystallization that accounts for the large increase in modulus at high deformation because the crystallites act as additional cross-links in the network. From this point of view, strain-induced crystallization can be considered as an auto-reinforcement of the elastomer. Those elastomers that cannot undergo strain-induced crystallization, are generally compounded with additives consisting of fillers like carbon black or silica in order to increase the modulus, tensile strength and wear resistance of the rubber material [
2,
3,
4,
5]. However, high loading levels of conventional fillers (often above 40 phr, “phr” = parts per 100 parts of rubber by weight) are required to achieve the desired properties.
Over the past few years, nanofillers have been extensively used in rubber nanocomposites on account of their small size and the corresponding increase in the surface area allowing significant improvement in the matrix properties at low filler loadings. The state of filler dispersion and orientation in the matrix, their size and aspect ratio as well as the interactions with the polymer chains, have been shown to be crucial parameters that determine the reinforcing ability of these nanoparticles.
Isodimensional nanofillers (SiO
2 or TiO
2) are spherical particles that can be generated in situ through a sol-gel process in the polymer. This process has proved to be a simple and efficient approach for the synthesis of composites where the reinforcing phase is finally dispersed within the polymer matrix which is a basic requirement for achieving optimum reinforcement [
6,
7,
8].
Among the nanometer-scale reinforcing particles, layered silicates have attracted a tremendous interest due to the considerable property improvements that could result if an exfoliated structure is obtained with a full separation of the clay layers leading to a large interfacial contact area with the polymer [
9].
The past ten years have seen an increased interest for rod-shaped nanofillers and essentially for carbon nanotubes. The recognition of their unique properties has stimulated a huge interest in their use as advanced filler in composite materials [
10,
11]. In particular, their superior mechanical, thermal and electrical properties are expected to provide much higher property improvement than other nanofillers. For example, as conductive inclusions in polymeric matrices, carbon nanotubes shift the percolation threshold to much lower loading values than traditional carbon black particles.
Besides carbon nanotubes, there is a great interest in graphitic nanostructures including graphite intercalation compounds, expanded graphite, graphite nanoplatelets, graphene and graphene oxide. Their use as reinforcing fillers for elastomeric materials holds great promise as a particular class of nanocomposites if the layered structure of graphite, similar to that of layered silicate, is exfoliated and if the separated nanosheets are well dispersed in the polymeric matrix [
12,
13,
14,
15,
16].
The focus of this paper is to highlight the state of knowledge in the carbon nanostructures, the properties, challenges and potential applications of elastomeric matrices filled with these carbon nanomaterials.
3. Manufacturing Techniques of Rubber Nanocomposites
Most preparation methods of nanocomposites aimed at achieving throughout the polymer matrix, a homogeneous and uniform filler dispersion. The state of filler dispersion is well known to play a major role on the final properties of the material and also to be influenced by the nature of the polymer-filler interactions. Besides the fillers, the rubber needs to be compounded with several other additives including curing agents, antioxidants, processing aids and coupling agents. The curing process that leads to the formation of a crosslink network may be affected by the presence of filler. Melt mixing, solution blending and in situ polymerization are the most commonly reported techniques in the literature for the preparation of carbon-based elastomeric composites.
In melt intercalation, compounding takes place in the molten state, by using conventional mixing devices (internal mixer, extruder, two-roll mill). This technique that does not require any solvent, is favoured by industry but may lead to a poor dispersion on account of the high viscosity of the composite that increases with filler fractions. Higher shear mixing often used to overcome the viscosity of the medium, may damage the filler structure which is detrimental to the composite properties.
Solution mixing is one of the most widely reported technique in academic researches for the processing of polymer nanocomposites because it ensures a better dispersion of the filler in the elastomeric matrix than melt processing. This technique cannot be applied in industry on account of the large quantities of solvents needed for the fabrication of the composites. It involves the dispersion of the filler particles in a suitable solvent by magnetic stirring, high shear mixing or sonication. The filler dispersion is then mixed with the rubber already in solution with all the additives for vulcanization. The two solutions are mixed together and the cross-linking process and film formation can be achieved after total removal of the solvent. But some carbon-based materials can be directly dispersed in polymers that are fluid at room temperature like low molecular weight poly(dimethylsiloxanes) before proceeding to the curing reaction [
21]. A polymer latex instead of a polymer solution has been used for the synthesis of rubber-clay nanocomposites by co-coagulating the rubber latex and a clay aqueous suspension [
22,
23,
24]. The composites prepared by the latex route have been shown to display a fine dispersed phase structure and good mechanical properties. Nevertheless, Wu et al. [
24] mention the presence of non-exfoliated layer aggregates resulting from re-aggregation of exfoliated clay layers during the process of co-coagulating. The layers of graphene-based materials are expected like in layered silicates, to be separated from each other in water and to be mixed uniformly with the rubber latex particles. The latex mixing and co-coagulation process has been applied by Zhan et al. [
25] then by Potts et al. [
26] for the preparation of reduced graphene oxide/natural rubber nanocomposites.
In situ polymerization that involves polymerization of the monomer previously mixed with the filler particles, generally leads to good level of dispersion of the inorganic material and good interactions between the two phases. Waterborne polyurethane polymerized in the presence of functionalized graphene sheets have been shown to give nanocomposites with higher reinforced properties than those made by a simple mixing method [
27]. Paszkiewicz et al. [
28] also show that graphene oxide was well exfoliated into individual sheets in composites fabricated through in situ polymerization.
The three different methods: melt compounding, solution blending and in situ polymerization, have been compared, for the synthesis of polyurethane filled with carbon sheets exfoliated from graphite oxide via two different processes: chemical modification and thermal exfoliation [
29]. It is demonstrated that exfoliated carbon sheets can be better dispersed in polymers using solvent aided blending, thus enhancing solid properties more effectively but economical and environment limitation makes the solvent-based processes less desirable. According to the authors, melt blending can be done rapidly and economically with conventional polymer extrusion processes despite the poor level of filler dispersion.
It has to be mentioned that other approaches intended to modify the filler surface, have been developed in order to reduce the tendency of carbon-based particles to assemble into agglomerates. Chemical bonding between the filler and the polymer chains enhances interfacial interactions between the two components but disrupts the delocalized π-electron system and affects the electrical properties. The use of surfactants acting as a non-covalent treatment has been shown to be an effective way to ensure homogeneous and stable dispersion throughout a solvent and in composite host materials [
30,
31]. This non-covalent modification of the carbon species is of great advantage because no disruption of the sp
2 graphene structure occurs and the filler properties are preserved contrary to covalent functionalization. But Dyke and Tour [
32] explain that in the case of carbon nanotubes, exfoliation of the bundles must occur previous to surface treatment in order to obtain individual tubes because the outermost nanotubes in a bundle are probably more treated than the innermost tubes. In that case, the nanotubes remain predominantly bundled after the surfactant treatment. This statement has been confirmed for MWCNT/polystyrene (PS) composites prepared in the absence and presence of a surfactant added before the sonication process [
33]. A transmission electron microscopy (TEM) analysis reveals the formation of ropes made of several nanotubes entangled together upon application of a surfactant while an almost random distribution with some remaining agglomerates nevertheless, is observed without any treatment (
Figure 1). This points out that the adsorption of the surfactant by the carbon species should occur after the dispersion process in order to get a surfactant- and polymer-stabilized system.
Incorporating simultaneously mixtures of two different fillers has been shown to improve the state of dispersion and promotes the formation of a continuous hybrid filler network resulting in better mechanical properties and, in the case of mixtures of carbon-based particles, in better electrical conductivity than composites filled with any single filler [
34,
35].
Figure 2 displays a TEM image of a styrene-butadiene rubber (SBR) filled with a dual loading (5 phr of CB + 5 phr of MWCNTs) in which carbon nanotubes are seen to connect CB aggregates. The double filling method was also used by Zhan et al. [
36] who prepared CB and CNTs filled nanural rubber (NR) composites through an ultrasonic assisted mixing process then by Galimberti et al. [
13,
14,
37] who add minor amounts of nanofillers (MWCNTs, nano graphite or organoclay) to a polyisoprene heavily filled with CB (60 phr). In all cases, the authors report synergistic effects between the two different types of fillers and initial modulus values much larger than those calculated by simple addition of the two initial moduli of the composites containing only a unique filler. An interesting application of the use of hybrid filler is the incorporation of small amounts of CNTs in a high silica-filled rubber in order to bring to nonconductive systems, some electrical conductivity required for the development of antistatic materials [
38]. A synergistic enhancement of the percolation threshold has been reported by Sagalianov et al. [
39] in hybrid polymeric nanocomposites based on carbon nanotubes and graphite nanoplatelets. More recently, carbon nanofibers were incorporated into CB-silica composites in order obtain conductive thin coatings by reducing the carbon-black content [
40].
4. Tensile Properties
The first consequence of the incorporation of hard filler particles in a soft polymeric medium is the increase in the elastic modulus. Another contribution can arise from polymer-filler interactions that leads to additional cross-links in the network structure. The increase in the effective degree of cross-linking can be evaluated by equilibrium swelling by a solvent and by measurements of chain orientation that has been shown to be sensitive to the chemical junctions and also to the number of polymer-filler attachments [
5,
41]. In silica-filled poly(dimethylsiloxane) (PDMS) rubbers for example, the interaction between the polymer and the filler is ensured by hydrogen bonds between the silanols present on the silica surface and the oxygen atoms of the PDMS chains. In order to meet application requirements and thus impart specific properties to the resulting material, the polymer-filler interface can be tailored by using treated silica in which part of the silanols are deactivated to decrease the interactions. The use of coupling agents in combination with silica, is commonly used in non-polar polymers like hydrocarbon rubbers, in order to enhance the degree of adhesion between the polymer and the filler [
42]. Due to their structural characteristics –high aspect ratio and high specific surface area that impacts the amount of interfacial area with the polymer- carbon nanostructures are expected to impart if they are finely dispersed in the elastomeric matrix, significant enhancements in various properties with regard to conventional fillers.
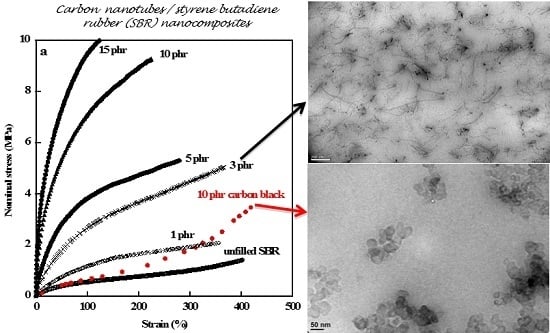
Hydrocarbon rubbers are commonly reinforced by CB and one specific feature brought by active fillers is the increase in stress observed at high deformations (see
Figure 3a the stress-strain curve of the SBR/10 phr CB composite). The increase in stress at high elongations is attributed to limited chain extensibility observed for the composite on account of the increase in the effective degree of cross-linking thus decreasing the apparent molecular weight between cross-links. This behavior that reflects the polymer-filler interactions is somewhat the signature of reinforcement. The abrupt increase in stress displayed by unfilled NR (
Figure 3b) is ascribed to the strain-induced crystallization of polymer chains that is an important characteristic of natural rubber due to its uniform microstructure. The crystallization process starts at a lower deformation in the presence of carbon black which may be regarded as resulting from a higher chain orientation in the direction of strain allowing the conformational change required for the formation of the crystallites [
43]. Chain orientation increases with additional cross-links created by NR-CB interactions. On the other hand, polymer chains are overstrained by strain amplification effects caused by the inclusion of undeformable filler particles [
44].
As seen in
Figure 3 that displays the stress-strain curves of SBR and NR composites, considerable improvement in stiffness, increasing with the filler loading, is imparted to both matrices by addition of multiwall carbon nanotubes (MWCNTs) with much higher levels of reinforcement than those provided by the conventional carbon black particles. But the CB-filled SBR sample exhibits an increase in stress at high strains contrary to the unfilled SBR that does not exhibit strain-induced crystallization. The data displayed in
Figure 3 were obtained from classical tensile tests performed at room temperature on a tensile Instron machine, model 5565 equipped with a 100 N load cell and a video extensometer. The strips (length around 20 mm between the jaws, width around 5 mm, and thickness between 200 and 300 μm) were marked with two dots with a white marker for their recognition by the video extensometer then stretched at a strain rate of 0.1 s
−1. The nominal stress σ was calculated from σ = f/A, where f is the elastic force and A is the undeformed cross-sectional area.
The stress-strain behavior of unfilled elastomeric networks has been reproduced by various theoretical models [
45,
46,
47,
48,
49]. A recent paper carried out a comparison of six different models in order to determine which of them represents the actual behavior of their material [
50]. It was concluded that the Mooney-Rivlin model [
45,
46] is the most accurate model to account for the mechanical behavior of Santoprene 101-73.
For the Mooney-Rivlin model, the nominal stress σ is given by:
where
λ is the extension ratio (ratio of the final length of the sample along the direction of stretch to that of the initial length before deformation) and 2
C1 and 2
C2 are constants independent of
λ. 2
C1 has been taken as an estimate of the high-deformation modulus (the phantom network model limit) and (2
C1 + 2
C2) has been used as an estimate of the low-deformation modulus (the affine network model limit) [
1].
In a Mooney-Rivlin representation, the reduced stress, [
σ*], defined by the quantity [
σ*] =
σ/(
λ −
λ−2) is plotted against of 1/
λ. Equation (1) was established for unfilled elastomers but it has been widely used in filled elastomeric materials (see Reference [
1] and all the papers of Mark et al. on filled elastomers and [
51]). Dannenberg [
52] explains that Equation (1) should apply to a filled vulcanizate if it can be assumed that the major function of the dispersed phase is to increase the effective strain of the rubber phase.
Mooney-Rivlin plots for unfilled and filled materials are displayed on
Figure 4. They are seen to better visualize specific features of the stress-strain curves. The upturn in the modulus observed at high deformations for the SBR/CB composite cannot be ascribed in this case to crystallization but to limited chain extensibility of chain bridging filler particles thus demonstrating strong interactions between carbon black and the elastomeric phase (
Figure 4a). The absence of upturn in the modulus at high elongations for the MWCNT/SBR composite denotes a weak polymer-filler interface and the strong decrease in stress observed at low deformations is attributed to the destruction of the filler network or at least of agglomerated filler structures. The Mooney-Rivlin plots of the NR/MWCNT composites display, at least for the lowest filler loadings, upturns in the modulus occurring at a lower extension ratio than that of NR/CB sample. According to the SBR results, the increase in stress at high deformations observed for the NR composites, is only attributed to the strain-induced crystallization of polymer chains. The question is to understand why the presence of fillers favors the crystallization process. In the case of CB as well as for MWCNTs, orientational effects can explain the decrease in strain values at the onset of crystallization. But an increase in chain orientation in the CB-filled composites can be attributed to a decrease in the apparent molecular weight between chemical and physical cross-links, in the case of MWCNTs, it probably arises from their strong ability to orientate along the direction of stretch. Orientation of anisotropic fillers that can be evidenced by TEM or AFM of stretched samples [
33,
53], is expected to affect the orientation of polymer chains as well and consequently the mechanical properties of the composite.
Ozbas et al. [
54] have compared the effect of functionalized graphene sheets (FGS) and that of carbon black on the strain-induced crystallization of NR by coupled tensile tests and X-ray diffraction experiments. It is shown that only 1 wt % FGS imparts higher modulus and strength than 16 wt % CB (
Figure 5a) and induces crystallization at lower strain (ε = 1.25 for the FGS-NR sample and 1.75 for the CB-filled NR). The authors mention the significant contribution of the alignment of FGS upon stretching to the mechanical properties of the nanocomposites. Small angle X-ray scattering shows that FGS is aligned in the stretching direction, whereas CB does not show alignment or anisotropy (
Figure 5b). The ratio of the intensity at the equator (
I90°) to the intensity at the meridian (
I0°) becomes larger during stretching for both FGS-filled SBR and NR samples indicating that FGS sheets are oriented along the stretching direction, whereas anisotropy is not observed for CB (
Figure 5c).
A comparative investigation on strain induced crystallization for graphene and carbon nanotubes filled natural rubber composites was also carried out by Fu et al. [
55] on composites prepared by ultrasonically-assisted latex mixing. The incorporation of graphene is shown to result in a faster strain-induced crystallization rate and a higher crystallinity compared to CNTs. The authors conclude to stronger polymer-filler interactions in the graphene/NR composites than in CNTs/NR composites on the basis of their swelling behavior. But a swelling restriction by solvents could also arise from occluded rubber entrapped inside filler agglomerates. On the other hand, the small difference, reported by the authors, between the swelling ratio of the two types of composites is not consistent with the strong difference between their tensile properties thus showing that other parameters have to be taken into account.
In an interesting paper of Scotti et al. [
56], shape controlled spherical and rod-like silica nanoparticles with different aspect ratios were synthesized by a sol-gel method in order to prepare silica/SBR composites by the blending method. The authors studied the influence of the particle morphology on the reinforcing effect independently of the silica surface chemistry and considering the aspect ratio as the only geometrical variance. The increase of the reinforcing effect of the rod-like particles by increasing their aspect ratio is related to both the self-alignment of anisotropic particles along the major axis direction and to their very large filler/polymer interface, compared to that of spherical particles. It is demonstrated that the mechanical reinforcing effect is basically related to the formation of a continuous percolative network of silica nanoparticles.
The percolative network, formed when filler aggregates join together either by direct contact or via layers of polymer shell around them, occurs at very low concentrations with anisotropic filler particles. It is responsible of the strong increase in the composite initial modulus (
Figure 3) and of the strong decrease at low strains of the reduced stress (
Figure 4). Galimberti et al. [
37] who also report a detectable impact of carbon nanotubes on the initial modulus of filled poly(1,4-cis-isoprene), apply the model of Huber and Vilgis [
57] that predicts that the excess of initial modulus (E − E
0)/E
0, where E and E
0 are the initial modulus of the composite material with and without CNTs respectively, has a linear dependence on the filler content below the percolation threshold and scales with a power low for higher concentrations (
Figure 6).
The inclusion of rigid particles is quantitatively taken into account by the Guth model [
58] only based on the aspect ratio,
f, and volume fraction,
φ, of filler. It has been widely used to estimate the change in modulus in filled elastomers, the quadratic term being added to account for filler-filler interactions:
E and
E0 are the moduli of the composite and the unfilled elastomer, respectively. The Guth equation predicts a strong increase in modulus at high volume fractions of filler.
A strong deviation from Equation (2) is expected at volume fractions above that corresponding to the formation of a filler network.
The data of
Figure 3 reveal a complete change in the stress-strain behavior of the MWCNT-filled rubbers with regard to the CB-filled samples, resulting in a significant increase of the stress at low strains and a considerable drop of the elongation at break. This fact has also been mentioned by Fritzche et al. [
38] and by Rooj et al. [
59].
The importance of the processing conditions on the properties of the final material is illustrated in the work of Yang et al. [
60] who studied composites of nitrile-butadiene rubber (NBR) filled with expanded graphite (EG) prepared by latex compounding and also by direct blending. It was shown that the tensile strength increases substantially with EG content for nanocomposites prepared by the latex compounding method (LCM) (
Figure 7a). The NBR/EG (10 phr) composite exhibits, as in
Figure 3, a strong increase in stress at low strains, and a much higher reinforcement efficiency than the composite prepared by blending and those reinforced with traditional fillers for rubbers such as carbon black and silica (
Figure 7b). The authors attribute the different tensile properties of NBR/EG vulcanizates prepared by latex compounding and direct blending to the different dispersion quality of graphite sheets. Additionally, polar groups on the EG surface (–OH and –COOH) are expected to interact with the polar cyanide group (C≣N) of the NBR macromolecular chains and form a strong interfacial adhesion. Interestingly, the ratio of the modulus at 100% elongation (σ 100%) of the NBR/EG (10 phr) sample prepared by latex compounding to that of the unfilled elastomer (σ
0 100%), is of the same order of magnitude as that of the SBR and NR composites filled with 10 phr of MWCNTs (
Figure 3). This ratio may be considered as a quantitative measure of the reinforcement effect.
All the above considerations lead to the belief that the reinforcement of rubber matrix in the presence of anisotropic filler particles depends mainly on the hydrodynamic effect arising from the inclusion of rigid particles, from their state of dispersion and their orientation under strain and from filler-filler interactions leading to the formation of a filler network. Almost all studies report a strong reduction of the strain at break most probably ascribed to the presence in the material, of remaining agglomerated structures that act as defects and failure points.
Filled and crystallizing unfilled elastomers display a characteristic stress-strain behavior after a pre-stretching. If the sample is uniaxially stretched to a given strain, ε
1, then released and stretched again to ε
2, released and stretched to ε
3…, reloading the sample leads to smaller stress values than those of initial loadings below the maximal strain values, thus exhibing the so-called stress-softening phenomenon known as the Mullins effect.
Figure 8 gives an example of four successive stretching cycles (shown in different colors) performed at various deformations on a poly(dimethylsiloxane) (PDMS) filled with 40 phr of silica.
Several interpretations have been proposed to explain the stress-softening of rubbers from breakage of both the filler clusters and the rubber-to-filler bonds, chain slippage process onto the filler surface, strain amplification to chain disentanglements [
44,
51,
61,
62,
63,
64,
65,
66,
67,
68,
69]. But despite the numerous studies devoted to an understanding of the Mullins effect, there is still no general agreeement on the origin of this effect probably because it may arise from different phenomena depending on the characteristics of the polymer-filler system. The literature on the Mullins effect was reviewed by Clément et al. [
70], Diani et al. [
71] and more recently by Harish et al. [
72].
On the basis of experiments based on atomic force microscopy under strain, Clément et al. [
70] showed that the Mullins effect is much more important with silica particles that has not undergone any surface treatment, in other words in particles that give rise to strong interaction with the PDMS chains. This points out the importance of the polymer-filler interface in systems with strong reactive components. The Mullins effect, in conventional composites, has been attributed to the breakage or the slippage, from the particle surface, of chains that attain their limit of extensibility by strain-amplification effects. Strain-amplification effects depend on the local volume fraction of filler around the polymer chains, in other words on the state of filler dispersion. On account of strain amplification phenomenon, the rubber is much more deformed in regions of the sample of high volume fractions of filler and consequently the chains reach their limit of extensibility at low strains and detach from the filler surface thus causing the loss of elastic chains. The other regions of lower filler volume fraction are not concerned at this stage of deformation but become affected at increasing strains. Atomic force microscopy carried out on stretched composites gives evidence that the strain field is highly heterogeneous, depending on the local concentration of filler and that the strain undergone by elastomer chains can be very high locally, in the regions where distances between aggregates are very short [
73]. The overstraining effects make chains to reach their limit of extensibility at low strains and detach from the filler surface resulting in a loss of elastic chains. It is worthwhile to notice that equilibrium swelling measurements performed on networks pre-stretched at different strains confirm the loss of elastic chains [
74,
75]. The concept of strain amplification was also used by Maiti et al. [
76] to analyze the Mullins softening in a silica-filled PDMS rubber material. The authors assume that during the first loading curve, the soft part of the matrix is being pulled out of the hard region thus progressively decreasing the relative fraction of the hard domain. The difference with the work of Clément et al. [
70] is the use of the spatially uniform strain amplification which is not correct since inhomogeneous strain fields were demonstrated by atomic force microscopy. Dargazany and Itskov [
77,
78] have proposed a micro-mechanical model for carbon-black fillers where damage of the polymer network is considered as a consequence of chain sliding on or debonding from aggregates.
Harish et al. [
72] have developed a heterogeneous (or multiphase) constitutive model by considering clustering and percolation behavior of filler particles. According to the authors, contrary to crystallizing unfilled elastomers for which crystallization leads to distinctive physical and chemical changes, in filled elastomers, filler breakage can be considered as one of the, if not primay, causes for Mullins softening. The filled elastomeric material is hypothesized as a three-phase material consisting of free rubber, bound rubber and filler aggregate phases but bound rubber properties are shown to not significantly impact the material response.
A very recent study [
79] uses strain-induced from mechanoluminescent cross-linkers in silica-filled poly(dimethylsiloxane) to demonstrate that covalent bond scission occurs predominantly on the first cycle to a particular strain, when the material displays the greatest hysteresis. The cross-linkers contain dioxetanes that emit light upon force-induced bond scission.
Elastomers filled with carbon nanomaterials (carbon nanotubes, graphite nanoplatelets or graphene oxide) have been shown to exhibit the Mullins stress-softening effect [
10,
35,
53,
80,
81,
82,
83,
84]. As mentioned in almost all studies, the important feature displayed by composites filled with carbon nanomaterials is the high degree of permanent deformation with regard to carbon black or silica-filled elastomers (
Figure 9).
Despite the fact that the existence of interactions between the graphene surface and the polymer chains is still a subject of debate, the different interpretations discussed above for conventional composites can be applied to explain the Mullins effect in samples filled with carbon nanomaterials. Nevertheless, one has to take into account their geometry and especially their high aspect ratio making them prone to get aligned when subjected to tension. Another significant effect of the strain is a debundling of the agglomerates resulting in a pulling out of the gum entrapped inside the agglomerates that reduces as mentioned in reference 76, the fraction of hard domains. This interpretation is supported by the fact that the rupture of the sample in the second stretching occurs at a much higher value of strain than that obtained in the first stretching curve [
85].
5. Dynamic Mechanical Properties
As reported above, the filler-filler interactions cause the formation of a filler network that enhances the modulus at low strains and is responsible of the strong decrease at low strains of the reduced stress (
Figure 4). The filler network is generally evidenced through the strain dependence of the storage modulus G’ that exhibits a non-linear behavior called the “Payne effect” [
86]. G’ displays a characteristic amplitude dependence, decreasing from the value of the modulus at strains approaching zero, G’
0, to a plateau value G’
∞ with increasing strain amplitude [
87]. The amplitude of the Payne effect defined as (G’
0 − G’
∞) has been found to be affected by the specific surface area, concentration and surface treatment of the filler particles as well as by the temperature. The Payne effect is obviously linked to the state of dispersion of the filler particles in the polymer matrix. The use of coupling agents in silica-filled hydrocarbon rubbers for example, decreases the amplitude of the Payne effect by depressing filler-filler interactions [
88]. In the case of an “ideal” dispersion as that obtained by the generation of filler particles by the sol-gel process, no Payne effect is observed in the whole range of shear strain range investigated (
Figure 10).
The drop in the elastic modulus has been mostly explained by a breakdown upon oscillatory shear, of the filler network formed by direct particle contacts or via immobilized elastomeric layer where the particle surface is recovered with adhering elastomeric molecules [
89]. Nevertheless, it has to be pointed out that a non-linear behavior can also be observed for filler volume fractions lower than the percolation threshold [
90] and from this point of view, below the percolation threshold, the Payne effect can be explained by a disruption of the filler agglomerated structures.
A Payne effect has been reported for elastomers filled with different carbon materials. In
Figure 11a that compares the Payne effect in NR composites filled with CB and MWCNTs, it is shown that the Payne effect strongly increases with the amount of filler and with the anisometry of the particles since it is much more important with MWCNTs than with CB at a same filler loading.
Surprinsingly, in poly(1,4-cis-isoprene) filled with a nanographite with a high shape anisotropy, a noticeable Payne effect is obtained for a filler content of 40 and 60 phr [
13], which corresponds to much higher volume fractions than those involved in NR/MWCNTs composites (see
Figure 11a) despite the high aspect ratio of nanographite, mentioned by the authors, expected to allow the formation of a filler network at a very low filler loading. The comparative non-linear dynamic viscoelastic response of neat NR and composites filled with CNTs alone and together with reduced graphene oxide, are shown in
Figure 11b. Graphene oxide (CG600 and CG20) was reduced thermally at two different temperatures 600 and 200 °C [
91]. The experimental results were fitted to the Maier and Göritz model based on filler-rubber interactions and on an adsorption mechanism of network chains on the surface of filler particles [
92]. The decrease of the dynamic storage modulus is attributed to a desorption of unstable bonded chains. It was deduced that the decrease in storage modulus with shear amplitude indicates an order of filler-rubber interaction as NR-CNT > NR-CG600 > NR-CG200 [
91]. Nevertheless, it has to be pointed out that the neat elastomer also displays a non-linear behavior contrary to what is expected and observed in
Figure 11a.
The results published in the literature do not allow to assess the influence of the nature of the anisotropic carbon particles on the Payne effect since the non-linear dynamic behavior is strongly related to the state of dispersion. Agglomeration leads to an increase in the volume fraction corresponding to the formation of a three-dimensional network structure that signicantly affects the dynamic viscoelastic properties. At this point, it is interesting to mention that in the work of Scotti et al. [
56] dealing with shape controlled and rod-like nanoparticles with different aspect ratios in SBR, the storage modulus at low strains, G’
0, increases with the aspect ratio but the G’
∞ values are very similar for all the composites filled at a same filler loading. This means that the differences in reinforcement are less effective once the network is broken down which was expected since the filler synthesis has been targeted to obtain nanoparticles only different in shape.
Temperature dependences of the storage modulus and of the loss factor, tand δ, are displayed in
Figure 12 for SBR/MWCNTs composites (a) and for NR composites filled with functionalized graphene sheets (FGS) (b). For all the samples, the strong decrease in the storage modulus is associated with the glass transition phenomenon of the elastomer chains. Below and above T
g, the value of E’ increases with increasing nanotube loading but the increase in the rubbery region is much more important than in the glassy state because it contains the contribution arising from the Payne effect [
93]. Dynamic mechanical results reported by Ozbas et al. [
54] for NR composites show a much higher increase in the storage modulus for NR filled with 4 wt % FGS (functionalized graphene sheets) than for a loading of 16 wt % CB even at four times lower volume fraction (
Figure 12b) which confirms the results displayed on
Figure 11a. The authors believe that in the rubbery region, strain amplification combines with the effect of immobilized rubber to give the 30- to 90-fold increases in the effective volume fraction. Nevertheless, it is also shown that Tg is not substantially shifted by the addition of either FGS or CB. Two papers of Araby et al. [
94,
95] in which graphene platelets (GnPs) have been incorporated in EPDM [
94] and in SBR [
95] observe an increase in the storage modulus by 2536% and 159% at 12 vol % GnPs in EPDM and around 190% and 650% at 10.5 vol % in SBR in the glassy and rubbery regions, respectively. These improvements are attributed to a high level of interaction between matrix chains and GnPs. However, it should be mentioned that the filler contents used in these studies and expressed in vol % are high while nanofillers, if well dispersed, are expected to impart to the host matrix strong reinforcement at very low filler loading. Besides the impressive and unusual enhancement of the storage modulus of the EPDM/GnPs (12 vol %), the authors mention an increase in T
g by 2.2% for the 5.7 vol % GnPs and an increase of 4 °C at 10.5 vol % GnPs in SBR, attributed to a decrease in the mobility of elastomer chains attributed to good interfacial polymer-filler interaction [
94,
95]. Potts et al. [
26] have shown that for a 5 wt % reduced graphene oxide/NR nanocomposite, the storage modulus increases by a factor of 3.4 and 2 at −100 °C, but by factors of 19.5 and 4.7 at 25 °C by solution treatment and two-roll mill processing. Analysis of tan δ peaks showed little to no change in T
g with loading but the authors mention that the shape and height of the peak change significantly with incorporation of GO platelets which they attribute to favorable polymer-filler interactions. Wu et al. [
96] also prepared a series of NR/GO composites filled with different GO sizes through latex co-coagulation technology in order to evaluate the effect of GO size on the mechanical properties of the resulting composites. The storage modulus at 20 °C of neat NR and of the composites filled with 2 phr of GO having three different sizes (92.68, 164.39 and 323.74 nm in the composites) are 1.01, 1.82, 1.71 and 1.52 MPa, respectively. The enhancement of the storage modulus is modest with regard to that observed by Potts et al. [
26].
All the studies reported above, point out some discrepancies and contradictory results due to the fact that the composite properties are affected by several factors including the type of particles, the type of polymer, the interfacial interactions and more significantly the filler dispersion that depends on the processing techniques.
6. Electrical Properties under Strain
Measurements of resistivity under strain brings further insight into the physical processes involved in deformation of filled elastomers. Carbon nanomaterials have largely demonstrated their ability to provide, when incorporated into ordinarily insulating polymeric media, electrical conduction at a much lower filler content than carbon black particles [
12,
16,
35,
97,
98,
99,
100,
101,
102,
103,
104]. At a given amount of conductive particles called the percolation threshold, a continuous network of filler is formed across the matrix and the material undergoes a sudden transition from an insulator to a conductor. The percolation threshold in various elastomers (NR, SBR and EPDM) filled with MWCNTs has been found to be around 0.5 phr [
102]. It has also been found to be 0.5 phr by Al-solamy et al. [
105] in acrylonitrile butadiene rubber filled with graphite nanoplatelets. In the review of Potts et al. [
101], the reported electrical percolation thresholds achieved with graphene-based nanocomposites do not differ significantly from those observed for CNT/polymer composites. Sadasivuni et al. [
12] report more dispersed values of the percolation threshold for graphene and graphite derivative elastomer nanocomposites.
Filler parameters such as particle size, structure, concentration, dispersion, orientation, are key factors in determining the electrical properties of composites. Resistivity is also sensitive to a mechanical deformation that changes the filler distribution. A typical strain dependence of volume resistivity of a NR/MWCNTs (3phr) composite is shown in
Figure 13. At the filler content of 3 phr, the composite is above the percolation threshold, determined around 0.5 phr [
102]. During the first stretching to 100% strain (step 1), the resistivity increases gradually thus reflecting a decrease in the filler contacts. This result may be regarded as arising from an alignment of filler structures in the stretching direction. White et al. [
103] have presented a three-dimensional simulation and calculation of electrical conductivity above the percolation threshold for networks containing finite, conductive cylinders as a function of axial orientation. It is shown that at a fixed volume fraction and aspect ratio, the electrical conductivities exhibit a substantial drop with increasing axial alignment. As the rods become highly aligned, the network structure is destroyed, causing the electrical conductivity to decrease. The authors highlight the importance of axial orientation of conductive cylindrical particles in a nonconductive matrix in determining the electrical conductivity and more generally in determining composite properties.
Figure 13 shows that unloading gradually the sample leads to an uncrease in resistivity and after total removal of the stress, the resistivity is much higher than that of the undeformed material thus showing that the contacts are not reformed. A second stretch is totally reversible till the point where the first and second stretching meet (step 2) then the resistivity increases again (step 3). A second unloading from ε = 200% leads to a higher value of resistivity than that obtained in the first unloading cycle and a third stretching still displays a decrease (step 4) then increase (step 5) in resistivity. The distance between particles increases along the direction of stretch but the width and thickness are reduced but increase upon unloading till zero stress causing a loss of contacts between conductive particles and an increase in resistivity. Re-straining the sample brings again the particles in the cross-sectional area into contact thus explaining the reversible portion of the curve in
Figure 13 (steps 2 and 4).
In a study related to the resistivity behavior of carbon black-filled silicone rubber submitted to cyclic loading experiments, Kost et al. [
104] showed, from stress and relative electrical resistivity relaxation experiments that upon complete retraction of the sample that follows stretching step, the resistivity is higher than the original value of the unstrained virgin sample. According to the authors, during cyclic tests, orientation effects are insignificant at low extensions (less than about 25%) where the formation and destruction of the carbon network is the dominant process. At higher strains, orientation effects become important, causing a resistivity reduction.
Elastomeric composites based on ethylene-propylene-diene monomer (EPDM) filled with MWCNTs have also been shown to display a decrease in conductivity with increasing strain, a linear relation being found between conductivity and deformations up to 10% strain [
98]. Cyclic experiments showed that the change in resistivity presents a reversible portion attributed to piezoresistivity and an irreversible one attributed to damage.
De Focatiis et al. [
81] have compared the resistivity-strain response of elastomers filled with CB to materials filled with MWCNTs. In the CB-filled elastomers, the piezoresistive loading path was relatively independent of prestrain, whereas the unloading path depended strongly on prestrain. In the MWCNT-filled elastomers, the piezoresistive loading and unloading paths were relatively close to each other. Cyclic experiments reveal that the resistivity was lower during loading than during unloading in the CB-filled materials whereas the reverse was true for the MWCNT-filled elastomers. The authors believe that the different behavior may be related to the very different aspect ratio of the filler particles. The cyclic experiments were intended to explore the applicability by the materials as strain sensors by looking for ranges of deformation where the electrical response was repeatable.