First-Principles Modeling of Atomic Structure and Chemical and Optical Properties of β-C3N4
Abstract
:1. Introduction
2. Computational Method
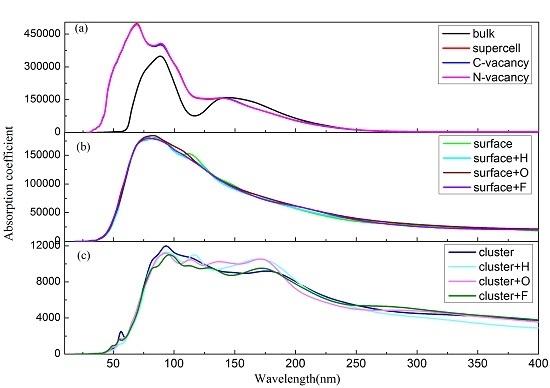
3. Results and Discussions
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Teter, D.M.; Hemley, R.J. Low-Compressibility Carbon Nitrides. Science 1996, 271, 53–55. [Google Scholar] [CrossRef]
- Liu, A.Y.; Cohen, M.L. Prediction of new low compressibility solids. Science 1989, 245, 841–842. [Google Scholar] [CrossRef] [PubMed]
- Kundoo, S.; Banerjee, A.N. Synthesis of crystalline carbon nitride thin films by electrolysis of methanol—Urea solution. Mater. Lett. 2002, 57, 2193–2197. [Google Scholar] [CrossRef]
- Yu, D.L.; Xiao, F.R.; Wang, T.S. Synthesis of graphite-C3N4 crystal by ion beam sputtering. J. Mater. Sci. Lett. 2000, 19, 553–556. [Google Scholar] [CrossRef]
- Sharma, A.K.; Ayyub, P.; Multani, M.S. Synthesis of crystalline carbon nitride thin films by laser processing at a liquid-solid interface. Appl. Phys. Lett. 1996, 69, 3489–3491. [Google Scholar] [CrossRef]
- Niu, C.; Lu, Y.Z.; Lieber, C.M. Experimental realization of the covalent solid carbon nitride. Science 1993, 261, 334–337. [Google Scholar]
- Montigaud, H.; Tanguy, B.; Demazeau, G. C3N4: Dream or reality? Solvothermal synthesis as macroscopic samples of the C3N4 graphitic form. J. Mater. Sci. 2000, 35, 2547–2552. [Google Scholar] [CrossRef]
- Hu, C.C.; Wang, M.S.; Guo, Z.W. Carbon Nitride (C3N4) Photocatalysts Synthesized from Different Methods for Photocatalytic Reaction Under Visible Light Irradiation. ECS Trans. 2016, 72, 9–14. [Google Scholar] [CrossRef]
- Yu, K.M.; Cohen, M.L.; Hailer, E.E.; Hansen, W.L.; Liu, A.Y.; Wu, I.C. Observation of crystalline C3N4. Phys. Rev. B 1994, 49, 5034–5037. [Google Scholar] [CrossRef]
- Cayuela, A.; Soriano, M.L.; Carrillo-Carrión, C.; Valcarcel, M. Semiconductor and carbon based fluorescent nanodots: The need for consistency. Chem. Commun. 2016, 52, 1311–1326. [Google Scholar] [CrossRef]
- Messina, F.; Sciortino, L.; Buscarino, G.; Agnello, S.; Gelardi, F.; Cannas, M. Photoluminescence of carbon dots embedded in a SiO2 matrix. Mater. Today Proc. 2016, 3, S258–S265. [Google Scholar]
- Liu, S.Q.; Liu, R.L.; Xing, X.; Yang, C.Q.; Xua, Y.; Wu, D.Q. Highly photoluminescent nitrogen-rich carbon dots from melamine and citric acid for the selective detection of iron(III) ion. RSC Adv. 2016, 6, 31884–31888. [Google Scholar] [CrossRef]
- Sciortino, L.; Messina, F.; Buscarino, G.; Agnello, S.; Cannas, M.; Gelardi, F.M. Nitrogen-doped carbon dots embedded in a SiO2 monolith for solid-state fluorescent detection of Cu2+ ions. J Nanopart. Res. 2017, 19, 228. [Google Scholar] [CrossRef]
- Messina, F.; Sciortino, L.; Popescu, R.; Venezia, A.M.; Sciortino, A.; Buscarino, G.; Agnello, S.; Schneider, R.; Gerthsen, D.; Cannas, M.; et al. Fluorescent nitrogen-rich carbon nanodots with an unexpected β-C3N4 nanocrystalline structure. J. Mater. Chem. C 2016, 4, 2598–2605. [Google Scholar] [CrossRef]
- Sciortino, L.; Sciortino, A.; Popescu, R.; Schneider, R.; Gerthsen, D.; Agnello, S.; Cannas, M.; Messina, F. Tailoring the Emission Color of Carbon Dots Through Nitrogen-Induced Changes of Their Crystalline Structure. J. Phys. Chem. C 2018, 34, 19897–19903. [Google Scholar] [CrossRef]
- Sciortino, A.; Mauro, N.; Buscarino, G.; Sciortino, L.; Popescu, R.; Schneider, R.; Giammona, G.; Gerthsen, D.; Cannas, M.; Messina, F. β-C3N4 Nanocrystals: Carbon Dots with Extraordinary Morphological, Structural, and Optical Homogeneity. Chem. Mater. 2018, 30, 1695–1700. [Google Scholar] [CrossRef]
- Faggio, G.; Gnisci, A.; Messina, G.; Lisi, N.; Capasso, A.; Lee, G.H.; Armano, A.; Sciortino, A.; Messina, F.; Cannas, M.; et al. Agnello, Carbon Dots Dispersed on Graphene/SiO2/Si: A Morphological Study. Phys. Status Solidi A 2019, 216, 1800559. [Google Scholar] [CrossRef]
- Fan, Q.Y.; Chai, C.C.; Wei, Q.; Yang, Y.T. Two Novel C3N4 Phases: Structural, Mechanical and Electronic Properties. Materials 2016, 9, 427. [Google Scholar] [CrossRef]
- Yao, H.Y.; Ching, W.Y. Optical properties of β-C3N4 and its pressure dependence. Phys. Rev. B 1994, 50, 11231–11234. [Google Scholar] [CrossRef]
- Xu, Y.; Gao, S.P. Band gap of C3N4 in the GW approximation. Int. J. Hydrogen Energy 2012, 37, 11072–11080. [Google Scholar] [CrossRef]
- Cohen, M.L. Structural, electronic and optical properties of carbon nitride. Mat. Sci. Eng. A 1996, 209, 1–4. [Google Scholar] [CrossRef]
- Liu, A.Y.; Cohen, M.L. Structural properties and electronic structure of low-compressibility materials: Si3N4 and hypothetical C3N4. Phys. Rev. B 1990, 41, 728–734. [Google Scholar] [CrossRef] [PubMed]
- Bonaccorso, F.; Sun, Z.; Hasan, T.; Ferrari, A.C. Graphene photonics and optoelectronics. Nat. Photonics 2010, 4, 611–622. [Google Scholar] [Green Version]
- Ahmadivand, A.; Gerislioglu, B.; Noe, G.T.; Mishra, Y.K. Gated Graphene Enabled Tunable Charge–Current Configurations in Hybrid Plasmonic Metamaterials. ACS Appl. Electron. Mater. 2019, 1, 637–641. [Google Scholar] [CrossRef]
- Fang, J.; Wang, D.; DeVault, C.T.; Chung, T.-F.; Chen, Y.P.; Boltasseva, A.; Shalaev, V.M.; Kildishev, A.V. Enhanced Graphene Photodetector with Fractal Metasurface. Nano Lett. 2017, 17, 157–162. [Google Scholar] [CrossRef] [PubMed]
- Ahmadivand, B.; Gerislioglu, Z. Ramezani Gated graphene island-enabled tunable charge transfer plasmon terahertz metamodulator. Nanoscale 2019, 11, 8091–8095. [Google Scholar] [CrossRef] [PubMed]
- Gerislioglu, B.; Ahmadivand, A.; Pala, N. Hybridized plasmons in graphene nanorings for extreme nonlinear optics. Opt. Mater. 2017, 73, 729–735. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, P.J.D.; Probert, M.J.; Pickard, C.J.; Hasnip, P.J.; Clarkand, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter. 2002, 14, 2717–2744. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. Lett. 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Bao, L.; Liu, C.; Zhang, Z.L.; Pang, D.W. Photoluminescence-Tunable Carbon Nanodots: Surface-State Energy-Gap Tuning. Adv. Mater. 2015, 27, 1663–1667. [Google Scholar] [CrossRef] [PubMed]







© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, X.; Boukhvalov, D.W.; Zatsepin, A.F. First-Principles Modeling of Atomic Structure and Chemical and Optical Properties of β-C3N4. C 2019, 5, 58. https://doi.org/10.3390/c5040058
Lei X, Boukhvalov DW, Zatsepin AF. First-Principles Modeling of Atomic Structure and Chemical and Optical Properties of β-C3N4. C. 2019; 5(4):58. https://doi.org/10.3390/c5040058
Chicago/Turabian StyleLei, Xue, Danil W. Boukhvalov, and Anatoly F. Zatsepin. 2019. "First-Principles Modeling of Atomic Structure and Chemical and Optical Properties of β-C3N4" C 5, no. 4: 58. https://doi.org/10.3390/c5040058
APA StyleLei, X., Boukhvalov, D. W., & Zatsepin, A. F. (2019). First-Principles Modeling of Atomic Structure and Chemical and Optical Properties of β-C3N4. C, 5(4), 58. https://doi.org/10.3390/c5040058