Next Article in Journal
Carbon Materials as Cathode Constituents for Electrochemical CO2 Reduction—A Review
Next Article in Special Issue
Pulling Simulations and Hydrogen Sorption Modelling on Carbon Nanotube Bundles
Previous Article in Journal
A Novel Mesoporous Carbon as Potential Conductive Additive for a Li-Ion Battery Cathode
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
C
Volume 5
Issue 4
10.3390/c5040082
carbon-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

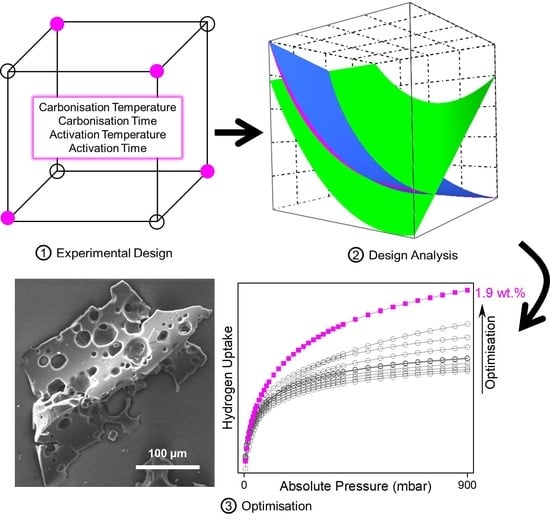
Application of Experimental Design to Hydrogen Storage: Optimisation of Lignin-Derived Carbons

by
Jemma L. Rowlandson
1,
James Coombs OBrien
2,3,
Karen J. Edler
2,
Mi Tian
4 and
Valeska P. Ting
1,*
1
Department of Mechanical Engineering, University of Bristol, Bristol BS8 1TR, UK
2
Department of Chemistry, University of Bath, Bath BA2 7AY, UK
3
Centre for Sustainable Chemical Technologies, University of Bath, Bath BS2 7AY, UK
4
Department of Chemical Engineering, University of Bath, Bath BA2 7AY, UK
*
Author to whom correspondence should be addressed.
C 2019, 5(4), 82; https://doi.org/10.3390/c5040082
Submission received: 12 November 2019 / Revised: 2 December 2019 / Accepted: 4 December 2019 / Published: 7 December 2019
(This article belongs to the Collection Carbon-Based Materials for Hydrogen Production, Storage and Conversion)
Browse Figures
Versions Notes

Abstract

:
Lignin is a significant by-product of the paper pulping and biofuel industries. Upgrading lignin to a high-value product is essential for the economic viability of biorefineries for bioethanol production and environmentally benign pulping processes. In this work, the feasibility of lignin-derived activated carbons for hydrogen storage was studied using a Design of Experiments methodology, for a time and cost-efficient exploration of the synthesis process. Four factors (carbonisation temperature, activation temperature, carbonisation time, and activation time) were investigated simultaneously. Development of a mathematical model allowed the factors with the greatest impact to be identified using regression analysis for three responses: surface area, average pore size, and hydrogen uptake at 77 K and 1 bar. Maximising the surface area required activation conditions using the highest settings, however, a low carbonisation temperature was also revealed to be integral to prevent detrimental and excessive pore widening. A small pore size, vital for efficient hydrogen uptake, could be achieved by using low carbonisation temperature but also low activation temperatures. An optimum was achieved using the lowest carbonisation conditions (350 °C for 30 min) to retain a smaller pore size, followed by activation under the severest conditions (1000 °C for 60 min) to maximise surface area and hydrogen uptake. These conditions yielded a material with a high surface area of 1400 m2 g−1 and hydrogen uptake of 1.9 wt.% at 77 K and 1 bar.

Graphical Abstract

1. Introduction

Lignin is a key component of lignocellulosic biomass, forming part of the plant cell walls [1]. This natural, highly aromatic biopolymer is a major waste product with over 70 million metric tons produced every year, primarily from the paper pulping industry [2]. Currently, lignin has no high-value application and is predominantly burnt as fuel [2,3]. The future economic viability of biorefineries for bioethanol production and environmentally benign pulping processes will depend on utilising this waste lignin and upgrading to high-value products. The conversion of lignin to activated carbon has received increasing attention due to its high carbon content (approximately 60 wt.%) and wide availability [4,5,6]. The use of lignin as a carbon feedstock could reduce the impact of greenhouse gas emissions associated with rotting or burning, as demonstrated for agroforestry waste [7]. The highly aromatic structure and availability of lignin also make it a potentially sustainable and economical replacement for the crude oil-based phenolic resin precursors widely used to produce high-value activated carbon materials [8,9].
Activated carbons are promising materials for the physisorptive storage of hydrogen, due to their low cost, high surface area, and ease of synthesis in bulk [10]. Activated carbons typically exhibit gravimetric hydrogen capacities of between 0.5 and 3.3 wt.% at 77 K and 1 bar, depending on the feedstock and synthesis conditions [11,12,13]. The preparation of activated carbons requires pyrolysis of a carbonaceous feedstock to form a char with a rudimentary pore structure. A chemical or physical activation procedure is then performed to enhance this porosity. Alternatively, both carbonisation and activation processes can be performed in one-step using a chemical agent [4,14,15,16]. Physical activation of the char using CO2 was chosen as the focus of this work, due to the lower environmental impact of the process in comparison to chemical activation [17,18,19,20]. Although production of activated carbons using either a chemical or physical activation method is an energy intensive process, the use of a low-carbon electricity system can cause a significant reduction in the associated global warming potential [19]. In the case of chemical activation, the impregnation of the chemical agent has significant environmental impacts in addition to those of the energy demand [20]. Physical activation with CO2 has previously been utilised to develop high surface area carbons (1000 to 3400 m2 g−1) with gravimetric hydrogen capacities of up to 2.3 wt.% at 77 K and 1 bar [21,22,23].
It is well established that hydrogen capacity tends to increase with material surface area, due to an increase in available adsorption sites [24,25]. As a general rule, gravimetric uptake of H2 at 77 K up to 1 bar increases by 1.1 wt.% for every 500 m2 g−1 of surface area the material has [11]. However, it has been shown that greater hydrogen uptake capacities can be achieved in materials with a large surface area composed of micropores (diameter less than 20 Å). In particular, narrow micropores between 5 and 7 Å allow for more efficient packing of adsorbed hydrogen at 77 K [25,26,27,28] with solid-like densities reported in micropores at temperatures up to 100 K and pressures as low as 0.2 bar [29]. The pore size distribution of a carbon is highly dependent on the processing conditions [17,30,31,32,33,34]. The impact of multiple factors (such as synthesis temperature, dwell time, and gas flow rate) means the investigation of how these parameters affect material properties, and their optimal levels are both challenging and time-intensive.
Design of Experiments (DoE) is a powerful tool which can be utilised for the optimisation of both carbonisation and activation processes simultaneously. Development of a mathematical model allows for the creation of a map of the material space, as well as the identification of interactions between the experimental factors, an outcome that cannot be achieved with the more traditional one-variable-at-a-time approach [35,36,37,38]. A fractional factorial design, where only half of the experimental runs of the full experimental design are required, can be employed for a time and cost-efficient exploration of the system whilst obtaining an increased level of information in comparison to traditional experimental approaches.
The focus of this work is to show how the combined use of a fractional factorial experimental design with high-throughput measurement methods is a valuable tool for rapid exploration of a new experimental system. An enhanced level of insight into the experimental system can be gained in a much shorter experimental time frame; identifying promising materials and evaluating the importance of chosen factors. A more detailed investigation into the most promising materials can then be performed. We examine the effect of four factors across both the carbonisation and activation processes at two levels; low and high. Lignin carbons were compared to an industrially produced phenolic-resin derived carbon, TE7, therefore the same physical activation agent (CO2) was chosen for consistency. High-throughput screening of the carbon materials employs three responses; Brunauer–Emmett–Teller (BET) surface area, average pore width derived from small-angle x-ray scattering, and hydrogen uptake at 77 K up to 1 bar. A more in-depth gas sorption analysis was then performed on the most promising materials identified by the experimental design.
The use of DoE for activated carbon optimisation has been utilised by several authors [30,31,39,40,41] primarily for water treatment. One of the few accounts of optimising lignin derived materials for hydrogen storage was published by Cheng et al. [42] who produced materials from hydrolytic lignin using chemical and physical activation, exhibiting hydrogen uptake of 2.0 to 2.6 wt.% at 77 K and 1 bar; however, further published research remains limited. To the authors’ knowledge, this is the first use of the DoE method for the optimisation of lignin materials for hydrogen storage.

2. Materials and Methods

2.1. Activated Carbon Preparation

Carbon materials were prepared from an organosolv lignin feedstock extracted from pine, supplied by MAST Carbon International (Basingstoke, UK). The lignin was used as provided, as a fine homogeneous powder. Carbonisation and activation of the lignin material was performed in a horizontal tube furnace (Lenton, Hope, UK, LTF 12/75/750) with a separate ceramic work tube and gas-tight end seals, fitted with a digital PID controller (Eurotherm, Worthing, UK, 3216CC). Mass flow controllers (Bronkhorst, Newmarket, UK, EL-FLOW) calibrated with a correlated flow meter (Cole Parmer, Vernon Hills, IL, USA, 32044-14) controlled the flow rate of gas into the furnace. PureShield argon (BOC, Guildford, UK, 99.998 % purity) with a flow rate of 500 mL min−1 was used as the inert furnace gas and a heating rate of 5 °C min−1 used throughout.
Lignin (3 g) was placed in an alumina combustion boat (20 mL capacity) and inserted into the centre of the furnace. The furnace was purged with argon for 30 min at room temperature, then heated to 105 °C and held for 30 min. The sample was then heated from 105 °C to the desired carbonisation temperature (between 350 and 900 °C), where it was held for the specified carbonisation dwell time (30 to 360 min) to produce a carbon char. The system was cooled to 350 °C at a rate of 1 °C min−1, then without rate control to room temperature. The carbon char was ground with a pestle and mortar and passed through a 35-mesh (500 μm) sieve. The ground char (1 g) was loaded into the furnace and heated under argon, as described previously, to the desired activation temperature (800 to 1000 °C). The furnace gas was switched to carbon dioxide (BOC, Guilford, UK, 99.998% purity) at 100 mL min−1 for the specified activation time (20 to 60 min) and then cooled in an argon atmosphere, as specified above.

Experimental Design

The optimal carbonisation and activation conditions were studied with a fractional factorial design (Resolution IV) based on four factors: carbonisation temperature (CTemp), carbonisation dwell time (CTime), activation temperature (ATemp), and activation dwell time (ATime). These factors were selected based on previous literature study specifically identifying factors with the most significant influence on adsorptive properties. Each factor was studied at a high (+1), low (−1), and midpoint (0) level, outlined in Table 1. The ranges were determined from values in the literature, except for activation dwell time which was chosen to ensure a range of burn-off levels, an accepted measure of the extent of activation [14,43,44], were considered and was determined using separate thermogravimetric experiments (see Figures S1 and S2 in the Supplementary Information). The factorial design is illustrated graphically in Figure S3 in the Supplementary Information. The minimum number of experiments for a two-level, four-factor design is 24 = 16. However, from only half of these experiments, the main effects and two-order interactions between the factors can be obtained, allowing the study of four factors at two levels in just 8 experimental runs. Consequently, all factors were varied simultaneously over 11 experiments: 8 variations plus 3 repeats; the experimental matrix is shown in Table 2. Individual experiments, and their resulting carbons, are referred to throughout the following as Exp X, where X corresponds to the experiment number listed in Table 2.
The effect of the combinations of the four factors on three responses was determined: BET surface area (SBET), average pore width derived from small-angle scattering (wavg: SAXS), and the hydrogen uptake at 77 K and 1 bar. The responses were chosen to allow efficient high-throughput screening of materials. A narrow pore size is important for hydrogen uptake and gas sorption is frequently used to investigate the pore size distribution of nanoporous materials. However, the collection of a full isotherm is time-intensive and unsuitable for screening large numbers of samples. The BET area is a good predictor of trends in hydrogen uptake within the same group of materials and has been shown to be a useful tool for approximating the number of adsorption sites [24,25]. Several authors have also previously shown a good correlation between the average pore size derived from SAXS and gas sorption [45,46,47]. Consequently, the BET area is used in the experimental design as a screening tool and SAXS was chosen to determine the average pore width of carbon materials.
Data evaluation was performed using the software MODDE Pro Version 11.0.2.2309 (Umetrics, Umeå, Sweden). The influence of factors was determined by fitting of a second-order polynomial model using partial least squares regression analysis [31,36]:
y = β 0 + ∑ i = 1 n β i x i + ∑ i = 1 n − 1 ∑ j = i + 1 n β i x i x j + ε
where y is the response, x terms are the factors, β0 is a constant term, β terms are the model parameters and ε is the residual response variation not explained by the model [31,35,36]. Determining numerical values for model parameters (β) established the impact of each factor on the measured response, and how said factors combined in influencing the response overall to determine the optimal process conditions [35,36].

2.2. Activated Carbon Characterisation

The surface area of chars and the adsorptive properties of select activated carbons were characterised by gas sorption analysis using a 3Flex analyser from Micromeritics (Norcross, GA, USA). Nitrogen (BOC, Guildford, UK, 99.999%) at 77 K or carbon dioxide (BOC, Guildford, UK, 99.999%) at 273 K was used as the adsorptive gas. Chars and activated carbons (50–100 mg) were degassed at 250 °C or 300 °C, respectively, for 4 h at dynamic 10−7 mbar vacuum. Isotherm data were collected up to 1 bar using filler rods from p/po 10−8–1 for N2 and p/po 10−5–10−2 for CO2. The p/po range for CO2 is limited in comparison to N2 due to its higher saturation pressure at 273 K [48,49]. Helium (BOC, Guildford, UK, 99.999%) was used to calculate the free space following isotherm collection. The BET surface area was calculated according to the procedure from ISO 9277:2010 [50]. Due to the highly microporous nature of samples, the Rouquerol correction was applied with the range p/po 0.01–0.03 and used to calculate the BET surface area. The performance of lignin-derived activated carbons and an industrially produced carbon TE7 (MAST Carbon International, Basingstoke, UK) was characterised by sorption of hydrogen (BOC, Guildford, UK, 99.999%) at 77 K. An identical procedure to the above was followed, except isotherms were collected using absolute pressure dosing from 5 to 900 mbar.
The pore size of activated carbons was screened using small-angle X-ray scattering (SAXS). SAXS measurements were performed at the University of Bristol using a Ganesha 300XL system (SAXSLAB, Copenhagen, Denmark) under vacuum to provide information on the average pore sizes. The instrument uses Cu K-α radiation (λ = 1.54 Å) and a two-dimensional Pilatus X-ray Detector. Activated carbon samples were loaded into 1.5 mm borosilicate–glass capillary tubes (Capillary Tube Supplies, Withiel, UK). Three 10 min measurements in different configurations were performed at room temperature on each sample to collect data over the range q = 0.004–2.6 Å−1. Data processing and background subtractions were performed using the program SAXSGUI by SAXSLAB. The three SAXS patterns were merged post-data processing using PRIMUS [51].
The low q part of the SAXS curve is often approximated by a single size parameter, the radius of gyration Rg [52]. For spherical pores with homogeneous density, the average pore width (wavg) can be calculated by [53].
w a v g = ( 5 3 R g )
Following the low q range examined by the Guinier approximation, higher values of q contain information regarding the nanoparticle shape. The scattering intensity falls off, in a region termed the “power law regime”, according to [52]:
I ( q ) ∝ q − n
where n is the fractal dimension and is dependent on the dimensions of the scattering particle. The scattering pattern oscillates in a manner characteristic of the particle shape (or form), known as the form factor P(q) [53]. Theoretical SAXS curves can be fitted to the collected pattern in order to describe the size and shape of scattering objects, and the interactions between them [52]. Scattering in activated carbons was first described by Kalliat et al. [54] and the model was later modified by Gibaud et al. [55]. The scattering intensity I(q) is related to the total surface area of macro A and micropores B, plus a constant background C:
I ( q ) = A q n + B ( 6 R g 2 + q 2 ) 2 + C
To examine the surface morphology of lignin chars, scanning electron micrographs (SEMs) were collected at the University of Bristol (JEOL UK, London, UK, IT300) in secondary electron mode at an accelerating voltage of 10–15 keV and a working distance of 10 mm.

3. Results and Discussion

3.1. Influence of Factors on Lignin-Derived Carbon Properties

In-depth characterisation of the organosolv extracted lignin feedstock was reported in the authors’ previous work [56]. The completed experimental design and measured responses are shown in Table 2. The raw data was evaluated using replicate plots (Figure S4 in the Supplementary Information). The measured variation between the three replicates was much smaller than the overall variation in the data set, indicating a small replicate error, which will not affect the results of regression analysis. Normally distributed data is advantageous for regression analysis, improving the efficiency of data analysis and enhancing model validity [35]. To this end, a logarithmic transformation was applied to the surface area response. No transformation was required for the average pore size response, and transformation did not affect the hydrogen uptake response (data distributions before and after transformation are included in Figure S5 in the Supplementary Information).

3.1.1. Activated Carbon Surface Area

The surface area of each activated carbon was determined by application of the BET equation to partial nitrogen isotherms. Repeat measurements for selected samples indicated a small measurement uncertainty for BET surface area of up to ±40 m2 g−1 (isotherms and BET fitting parameters are shown in Figure S6 and Table S1 in the Supplementary Information). Regression coefficients, showing the influence of factors on the activated carbon surface area, are illustrated in Figure 1a. Four factors were determined to influence the model validity: CTemp, ATemp, ATime, and the squared term ATemp*ATemp. Activation conditions were shown to have the greatest influence on the development of the BET surface area with the activation temperature and time having a positive effect i.e., increasing either led to an improved surface area. Increasing the activation temperature has been shown to cause an exponential increase in the rate of reaction between the carbon char and CO2 [15,57,58] as higher temperatures lead to a larger release of volatile matter from the char. Similarly, increasing activation time allows for the further reaction of CO2 with the char, also resulting in an increased emission of volatile matter. Both effects promote the creation of new porosity, leading to a higher burn off of the char and improving the surface area of activated carbons [17,18,30,31,34,59,60,61]. The positive squared term ATemp*ATemp implies a nonlinear relationship between surface area and activation temperature. This relationship is discussed in detail in Section 3.1.2; in brief, it is likely related to the rate of gasification.
Carbonisation temperature is shown in Figure 1a to have a negative effect; increasing the temperature leads to a reduction in BET surface area. Previous literature [32,33,59] has attributed such a negative effect to the formation of an “intermediate melt” at high carbonisation temperatures; secondary devolatilisation and redeposition of high molecular weight volatiles which can obstruct the passage of activation gas into the rudimentary porous structure of the char, adversely affecting activated carbon burn-off and adsorptive properties. The presence of an intermediate melt was examined for a high- and low-temperature lignin char, carbonised at 900 °C or 350 °C for 30 min (see Table 2, Exp 5 & Exp 6), using scanning electron microscopy and gas sorption.
No evidence of an intermediate melt was observed in SEM micrographs (Figure S7 in the Supplementary Information). N2 BET surface area results of the 900 °C and 350 °C chars (see Figure S8 in the Supplementary Information) also showed no presence of an intermediate melt; the high-temperature char has a larger BET surface area (150 m2 g-1) than the low-temperature char (<1 m2 g−1). Diffusion limitations of N2 into ultra-micropores (pores below 7 Å in width) at cryogenic temperatures are well-known phenomena [48,49]. Porosity inaccessible to N2 was examined using CO2 isotherms at 273 K (Figure 2), which corroborate the BET surface area results: the high-temperature char exhibits increased CO2 uptake in comparison to the low-temperature char, with a maximum uptake of 70 cm3 g−1 and 15 cm3 g−1, respectively, indicating the high-temperature char has an enhanced porous network, unhindered by an intermediate melt.
The negative effect of carbonisation temperature, consequently, likely results from the widening of existing porosity in the high-temperature char. On activation, this leads to an increased formation of meso- and micropores, which have a reduced contribution to surface area compared to micropores. Other authors [62,63] have also noted materials carbonised at low temperatures yield improved surface area in comparison to chars prepared at high temperature. This was linked to a larger micropore volume in the low-temperature chars, and an increased meso- and macropore volume in the high-temperature chars.
Response–contour surface plots can be used to gain a better understanding of how the critical factors identified by regression analysis affect the modelled system by giving a visual representation. The surface area response–contour plot is shown in Figure 3. The model predicts a linear response between all factors and the surface area, which is reflected in the response plot. In summary, materials with the highest surface area are obtained using extended activation dwell times, low carbonisation temperatures, and high activation temperatures.

3.1.2. Activated Carbon Average Pore Size

The activated carbon average pore size was screened using SAXS; patterns and fitting parameters are included in Figure S9 and Table S2 in the Supplementary Information. Regression coefficients, illustrated in Figure 1b, indicate carbonisation and activation temperature have the greatest influence on average pore size. Four factors were determined to influence model validity; CTemp, ATemp, the squared term ATemp*ATemp, and the interaction term CTemp*ATemp. The positive influence of carbonisation temperature on activated carbon pore size is consistent with the negative effect this factor exhibits on the surface area (Section 3.1.1). Increased carbonisation temperature leads to an enhanced porous network in the resulting char, as demonstrated by CO2 isotherms (Figure 2) of the 350 °C and 900 °C lignin chars. This porous network is enhanced in the activation step, widening porosity and broadening the average pore size [32,33,63]. Conversely, because low-temperature chars have a less extensive porous network, the pore widening effect is less dominant on activation, instead favouring the creation of new porosity and resulting in a smaller average pore size [30,33,63,64,65]. A similar effect, well-reported in the literature, occurs at high activation temperatures: the processes of pore widening and pore wall collapse are more dominant than the development of new micropores at higher activation temperatures, leading to a broadening of the average pore width. At low activation temperatures, the reverse has been observed, with pore creation the dominant process leading to a narrower pore width [17,18,30,31,59,60,66].
For average activated carbon pore size, regression analysis has highlighted the two-factor interaction term CTemp*ATemp as significant. A two-factor interaction is when the impact of one factor is dependent on the level of a second factor [35]. The negative CTemp*ATemp interaction implies broadening of the average pore size is greater at both high carbonisation temperature and high activation temperature. The effect on the system is demonstrated by the response–contour surface plot in Figure 4; the largest pore widths are obtained when these parameters are at their highest levels. This interaction is likely related to the negative effect of carbonisation temperature on activated carbon surface area. High-temperature chars have a more extensive porous network and larger pores than low-temperature chars. Activation increases this pore size further with higher temperatures contributing further to a broader pore size distribution [17].
The squared term ATemp*ATemp (first introduced in Section 3.1.1) in both the average pore size and BET surface area models exhibits large confidence intervals which cross the x-axis, indicating this term is statistically insignificant. However, removal of this term from either model is detrimental to the model validity, reducing the Q2 value. This behaviour indicates the term is important; however, the current model does not entirely account for the observed behaviour. ATemp*ATemp implies a positive, nonlinear relationship for both responses with the activation temperature. This relationship is likely related to the rate of CO2 activation, which is temperature-dependent, and known to increase exponentially below 1500 °C [15,57,58]. During activation, oxygen chemisorbs to active sites on the char surface. The reaction rate is proportional to the concentration of occupied sites, which is, in turn, dependent on the activation temperature and reactivity of the carbon surface [15,57]. Consequently, we theorise that burn-off, directly affecting pore size and surface area, could show the same exponential relationship as the reaction rate, although a more complex model is required to investigate this further.
The absence of carbonisation dwell time as a significant factor in Figure 1 indicates that CTime has little effect on either the activated carbon surface area or average pore width in this system. Previous research has highlighted the carbonisation dwell time as an important factor [30,33,63]. In this work, the irrelevance of CTime can be attributed to the small sample size (3 g), and relatively slow ramp rate (5 °C min−1) used throughout the experiments. The ramp rate is restricted to avoid cracking of the ceramic work tube in the furnace. Volatile emission occurs over a longer period at 5 °C min−1 in comparison to a rapid or flash pyrolysis (for example, at 20 °C min−1). Consequently, the ramp rate can be considered an extension of the dwell time. If complete emission of volatiles from the char (devolatilisation) occurs in this initial, slow ramping period, then the subsequent carbonisation dwell time becomes less significant.

3.1.3. Activated Carbon Hydrogen Uptake

The influence of factors on the hydrogen uptake at 77 K is illustrated in Figure 1c. Activation temperature and dwell time appear to have the greatest influence on activated carbon performance. Inclusion of the linear CTemp and squared ATemp*ATemp terms improves the model validity, indicating they are also significant. The influencing factors are akin to those affecting BET surface area, indicating for this system a large surface area is important for hydrogen uptake. The interplay between the three responses and the factors with the most significant influence (carbonisation and activation temperature) can be examined in Figure 5. Clearly, the hydrogen uptake and surface area responses exhibit analogous behaviour: maximum uptake is achieved in the material with the highest surface area. The adsorptive properties of the best-performing activated carbons (Exp 5 and Exp 8 in Table 2), with the largest BET surface area and H2 uptake, identified from the experimental design are examined in more detail using N2 sorption in Section 3.2.

3.1.4. Analysis of Model Fit

Model validity was assessed using R2 and Q2 parameters. Measured between 0 and 1, the parameters should be high and preferably separated by no more than 0.3 [35]. The agreement between model and experimental values for all responses was examined and is shown in Figure 6, with the parameters of ANOVA analysis listed in Table 3. For all responses, the experimental points are clustered close to the line predicted by the model, resulting in high R2 and Q2 values. The regression coefficient plots in Figure 1 show several terms in the pore size and hydrogen uptake models have large confidence intervals that cross the x-axis, indicating they are statistically insignificant. However, removal of these terms is detrimental to the model, indicating that while important, the model does not entirely account for the observed behaviour, leading to lower Q2 values. ANOVA analysis, however, indicates all models are statistically significant at the 95% confidence level (p < 0.05, for all models p ≤ 0.01), and the pore size model shows no lack of fit (p > 0.05, for this model p = 0.17).
ANOVA results indicate the H2 uptake and surface area models do exhibit a lack of fit (p < 0.05, for these models p ≤ 0.01). However, the high R2 and Q2 values for these models shows that this lack of fit is artificial; with a true lack of fit, both values would be small. Instead, this is caused by the excellent replicates obtained for surface area (512–518 m2 g−1) and hydrogen uptake (1.28–1.29 wt.%). Altering one of these values so there is more considerable variation between replicates (by 50 m2 g−1 or 0.1 wt.% for example) yields models with no lack of fit (p = ~0.2).

3.2. Adsorptive Characteristics of Optimal Activated Carbon

The processing conditions for Exp. 5 and Exp. 8 were identified as producing the best-performing materials; activated carbons exhibited the highest H2 uptake (1.9 wt.% and 1.6 wt.%, respectively, at 77 K and 1 bar) and BET surface area (1409 m2 g−1 and 1055 m2 g−1, respectively). The adsorptive properties of these materials were examined in more detail using N2 sorption. Both carbons exhibited an isotherm with typical Type I behaviour; adsorption primarily occurred at p/po < 0.1 (Figure S10 in the Supplementary Information).
The adsorptive properties of the carbon are displayed in Figure 7a and are at the higher end of those reported in the literature. Previous studies of lignin carbons from physical activation have reported BET surface areas of 46 to 1853 m2 g−1 and pore volumes of 0.01 to 0.83 cm3 g−1 [62,67,68,69,70,71]. Both carbons are highly microporous, with micropores contributing 84 % (Exp. 5) and 93 % (Exp. 8) to the total pore volume. The average pore size predicted by gas sorption (wavg: GSA) is smaller than the value derived from SAXS analysis (wavg: SAXS); 6.6 Å and 9.3 Å respectively for Exp. 5 and 7.4 Å and 10.0 Å respectively for Exp. 8. This small variation is due to differences in the measurement method; SAXS measures all porosity, whereas gas sorption only considers pores open to nitrogen. For this reason, although SAXS has proved efficient for high throughput screening, the volume-weighted average pore size derived from gas sorption is more applicable to H2 uptake capacity, because it considers only accessible porosity.
A pore size distribution, derived by the fitting of the 2D-NLDFT model to the N2 isotherm, is shown in Figure 7b. The pore size distribution for both the Exp. 5 and Exp. 8 carbons is centred around pores 5–6 Å in diameter, with further, smaller contributions to pore volume from porosity approximately 8 Å and 12 Å in diameter. However, widening of porosity in the Exp. 8 carbon is evident. The pore size distribution is shifted to slightly wider pores, which appears to have adversely affected the adsorptive properties (illustrated in Figure 7a), resulting in reduced BET surface area and total pore volume in comparison to Exp. 5.

3.3. Hydrogen Uptake of Optimal Activated Carbons

Hydrogen isotherms for the Exp 5 and Exp 8 activated carbons are shown in Figure 8a. For comparison, a well-characterised and industrially produced activated carbon, TE7, was also investigated [29,72,73]. TE7 is derived from crude oil-based phenolic resin; there is great interest in using the highly aromatic lignin as a cheap and sustainable replacement feedstock. There is minimal hysteresis between the adsorption and desorption branches of all isotherms, indicating adsorption was completely reversible. The lignin carbons exhibit a gravimetric hydrogen uptake of 1.6–1.9 wt.% and TE7 exhibits an uptake of 2.0 wt.%, comparable to previously reported values for this material [73].
The optimum pore size for efficient storage of hydrogen in micropores is between 5 and 7 Å [25,26,27,28]. For Exp. 5 and Exp. 8, micropores below 7 Å account for around 70 % and 60 % of the total pore volume, respectively. The increased H2 uptake observed for Exp. 5 (1.9 wt.%) can be attributed to the increased surface area and quantity of micropores in the material. The efficiency of these narrow micropores can be seen in Figure 8b; the Exp. 5 carbon prepared in this work outperforms materials in the literature with a higher surface area. The hydrogen uptake is comparable to the uptake of hydrolytic lignin carbons prepared by Cheng et al. (2000 m2 g−1, 2.0 wt.%) [42] despite a lower surface area. Importantly, the hydrogen uptake of Exp. 5 is on par with the industrially produced TE7, indicating that lignin could be a promising replacement for phenolic resin precursors. This work has shown organosolv lignin can be upgraded to a high value activated carbon, producing a material with a high surface area and reasonable hydrogen uptake at 77 K up to 1 bar.
Carbons produced using a chemical activation procedure exhibit a higher surface area (1800–2500 m2 g−1) and hydrogen uptake (1.6–3.3 wt.%) in comparison to the Exp. 5 and Exp. 8 lignin carbons [12,13,22,74,75,76,77,78]. The best-performing biomass- or lignin-derived activated carbons are shown to the right-hand side of Figure 8b; materials exhibit BET surface areas over 3000 m2 g−1 and large H2 uptake values of 2.3–3.3 wt.%. Despite their large hydrogen capacity, these materials exhibit a much broader pore size (from 8 to 40 Å) in comparison to the carbons in this work [13,21,22,42]. Consequently, the large hydrogen uptake can be attributed to their high BET surface area. Efficient hydrogen uptake, required to maximise both volumetric and gravimetric capacity, is reliant on increasing the BET surface area of a material whilst maintaining a narrow pore size of 5–7 Å [25]. The Design of Experiments approach has been shown to be a useful tool for exploring a new activated carbon process; able to handle multiple factors and resulting in valuable insights into the carbonisation and activation behaviour of a material. Future utilisation of this technique will be invaluable in enhancing the surface area of activated carbons whilst maintaining the narrow pore size required for hydrogen storage.

4. Conclusions

An investigation into the preparation of activated carbons from lignin utilising a Design of Experiments approach has provided valuable insight into the use of these materials for hydrogen storage. Regression analysis revealed that carbonisation and activation temperature had the most significant influence on the three measured responses; BET surface area, SAXS-derived average pore size, and hydrogen uptake at 77 K and 1 bar. The maximum surface area was obtained using the severest activation conditions (1000 °C for 60 min). However, a low carbonisation temperature (350 °C) was also important to minimise the effect of pore widening, which is detrimental to the material surface area. The lowest carbonisation and activation temperatures (350 °C and 800 °C, respectively) resulted in the smallest pore size. Maximum hydrogen uptake (1.9 wt.%) was obtained using the lowest carbonisation conditions (350 °C for 30 min), to retain a small pore size for efficient hydrogen packing, followed by activation under the severest conditions (1000 °C for 60 min) to maximise surface area (1400 m2 g−1). This work has shown the potential application of organosolv lignin as a feedstock to produce high surface area activated carbons for hydrogen storage. The Design of Experiments method provided valuable insight into this synthetic process and will be invaluable for the further optimisation of these materials to enhance the material surface area while maintaining narrow micropores.

Supplementary Materials

The following are available online at https://www.mdpi.com/2311-5629/5/4/82/s1, Table S1: BET fitting results, Table S2: SAXS fitting results, Figure S1: Thermogravimetric analysis of lignin char, Figure S2: Scale-up of thermogravimetric experiment to horizontal tube furnace, Figure S3: Graphical representation of a full factorial experimental design, Figure S4: Replicate plots, Figure S5: Histograms of response, Figure S6: Partial nitrogen isotherms recorded at 77 K for lignin-derived activated carbons, Figure S7: Scanning electron micrographs of lignin chars, Figure S8: Partial nitrogen isotherms recorded at 77 K for lignin chars, Figure S9: SAXS patterns of lignin-derived activated carbons, Figure S10: Nitrogen isotherms recorded at 77 K for lignin-derived activated carbons.

Author Contributions

Conceptualisation, J.L.R., V.P.T. and K.J.E.; methodology, J.L.R.; formal analysis & validation, J.L.R. and J.C.O.; investigation, J.L.R. and M.T.; writing—original draft preparation, J.L.R.; writing—review and editing, J.L.R., J.C.O., K.J.E., M.T. and V.P.T.; visualization, J.L.R.; supervision, V.P.T. and K.J.E.; project administration, J.L.R., V.P.T. and K.J.E.; funding acquisition, V.P.T.

Funding

This research was funded by the Engineering and Physical Sciences Research Council (EPSRC) via grant EP/R01650X/1.

Acknowledgments

The authors thank Steve Tennison at Carbon Tex Ltd. (formerly MAST Carbon) for supplying the organosolv lignin feedstock used in this work.

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Calvo-Flores, F.G.; Dobado, J.A. Lignin as renewable raw material. ChemSusChem 2010, 3, 1227–1235. [Google Scholar] [CrossRef] [PubMed]
  2. Dutta, S.; Wu, K.C.-W.; Saha, B. Emerging strategies for breaking the 3D amorphous network of lignin. Catal. Sci. Technol. 2014, 4, 3785–3799. [Google Scholar] [CrossRef]
  3. Meister, J.J. Modification of Lignin. J. Macromol. Sci. Part C Polym. Rev. 2007, 42, 235–289. [Google Scholar] [CrossRef]
  4. Carrott, P.J.M.; Carrott, M.R. Lignin-from natural adsorbent to activated carbon: A review. Bioresour. Technol. 2007, 98, 2301–2312. [Google Scholar] [CrossRef]
  5. Snowdon, M.R.; Mohanty, A.K.; Misra, M. A Study of Carbonized Lignin as an Alternative to Carbon Black. ACS Sustain. Chem. Eng. 2014, 2, 1257–1263. [Google Scholar] [CrossRef]
  6. de Wild, P.J.; Huijgen, W.J.J.; Heeres, H.J. Pyrolysis of wheat straw-derived organosolv lignin. J. Anal. Appl. Pyrolysis 2012, 93, 95–103. [Google Scholar] [CrossRef] [Green Version]
  7. Ntuli, V.; Hapazari, I. Sustainable waste management by production of activated carbon from agroforestry residues. S. Afr. J. Sci. 2013, 109, 1–6. [Google Scholar] [CrossRef] [Green Version]
  8. Busquets, R.; Kozynchenko, O.P.; Whitby, R.L.D.; Tennison, S.R.; Cundy, A.B. Phenolic carbon tailored for the removal of polar organic contaminants from water: A solution to the metaldehyde problem? Water Res. 2014, 61, 46–56. [Google Scholar] [CrossRef] [Green Version]
  9. Sharpe, J.E.; Bimbo, N.; Ting, V.P.; Rechain, B.; Joubert, E.; Mays, T.J. Modelling the potential of adsorbed hydrogen for use in aviation. Microporous Mesoporous Mater. 2015, 209, 135–140. [Google Scholar] [CrossRef] [Green Version]
  10. Yu, X.; Tang, Z.; Sun, D.; Ouyang, L.; Zhu, M. Recent advances and remaining challenges of nanostructured materials for hydrogen storage applications. Prog. Mater. Sci. 2017, 88, 1–48. [Google Scholar] [CrossRef]
  11. Sevilla, M.; Mokaya, R. Energy storage applications of activated carbons: Supercapacitors and hydrogen storage. Energy Environ. Sci. 2014, 7, 1250–1280. [Google Scholar] [CrossRef] [Green Version]
  12. Wang, J.; Senkovska, I.; Kaskel, S.; Liu, Q. Chemically activated fungi-based porous carbons for hydrogen storage. Carbon 2014, 75, 372–380. [Google Scholar] [CrossRef]
  13. Yang, R.; Liu, G.; Li, M.; Zhang, J.; Hao, X. Preparation and N2, CO2 and H2 adsorption of super activated carbon derived from biomass source hemp (Cannabis sativa L.) stem. Microporous Mesoporous Mater. 2012, 158, 108–116. [Google Scholar] [CrossRef]
  14. Bansal, R.C.; Donet, J.B.; Stoeckli, H.F. Active Carbon; Marcel Dekker: New York, NY, USA, 1988. [Google Scholar]
  15. Marsh, H.; Rodríguez-Reinoso, F. Activated Carbon; Elsevier: London, UK, 2006. [Google Scholar] [CrossRef]
  16. Świątkowski, A. Industrial Carbon Adsorbents. Stud. Surf. Catal. 1999, 120, 69–94. [Google Scholar] [CrossRef]
  17. Guo, S.; Peng, J.; Li, W.; Yang, K.; Zhang, L.; Zhang, S.; Xia, H. Effects of CO2 activation on porous structures of coconut shell-based activated carbons. Appl. Surf. Sci. 2009, 255, 8443–8449. [Google Scholar] [CrossRef]
  18. Yang, K.; Peng, J.; Xia, H.; Zhang, L.; Srinivasakannan, C.; Guo, S. Textural characteristics of activated carbon by single step CO2 activation from coconut shells. J. Taiwan Inst. Chem. Eng. 2010, 41, 367–372. [Google Scholar] [CrossRef]
  19. Arena, N.; Lee, J.; Clift, R. Life Cycle Assessment of activated carbon production from coconut shells. J. Clean. Prod. 2016, 125, 68–77. [Google Scholar] [CrossRef] [Green Version]
  20. Hjaila, K.; Baccar, R.; Sarrà, M.; Gasol, C.M.; Blánquez, P. Environmental impact associated with activated carbon preparation from olive-waste cake via life cycle assessment. J. Environ. Manag. 2013, 130, 242–247. [Google Scholar] [CrossRef]
  21. Li, Y.; Li, D.; Rao, Y.; Zhao, X.; Wu, M. Superior CO2, CH4, and H2 uptakes over ultrahigh-surface-area carbon spheres prepared from sustainable biomass-derived char by CO2activation. Carbon 2016, 105, 454–462. [Google Scholar] [CrossRef]
  22. Wang, H.; Gao, Q.; Hu, J. High hydrogen storage capacity of porous carbons prepared by using activated carbon. J. Am. Chem. Soc. 2009, 131, 7016–7022. [Google Scholar] [CrossRef]
  23. Bader, N.; Abdelmottaleb, O.N. CO2 activation of olive bagasse for hydrogen storage. Environ. Prog. Sustain. Energy 2017, 36, 315–324. [Google Scholar] [CrossRef] [Green Version]
  24. Xia, Y.; Yang, Z.; Zhu, Y. Porous carbon-based materials for hydrogen storage: Advancement and challenges. J. Mater. Chem. A 2013, 1, 9365–9381. [Google Scholar] [CrossRef]
  25. Masika, E.; Mokaya, R. Hydrogen storage in high surface area carbons with identical surface areas but different pore sizes: Direct demonstration of the effects of pore size. J. Phys. Chem. C 2012, 116, 25734–25740. [Google Scholar] [CrossRef]
  26. Gogotsi, Y.; Portet, C.; Osswald, S.; Simmons, J.M.; Yildirim, T.; Laudisio, G.; Fischer, J.E. Importance of pore size in high-pressure hydrogen storage by porous carbons. Int. J. Hydrog. Energy 2009, 34, 6314–6319. [Google Scholar] [CrossRef]
  27. Gogotsi, Y.; Dash, R.K.; Yushin, G.; Yildirim, T.; Laudisio, G.; Fischer, J.E. Tailoring of nanoscale porosity in carbide-derived carbons for hydrogen storage. J. Am. Chem. Soc. 2005, 127, 16006–16007. [Google Scholar] [CrossRef]
  28. Sethia, G.; Sayari, A. Activated carbon with optimum pore size distribution for hydrogen storage. Carbon 2016, 99, 289–294. [Google Scholar] [CrossRef]
  29. Ting, V.P.; Ramirez-Cuesta, A.J.; Bimbo, N.; Sharpe, J.E.; Noguera-Diaz, A.; Presser, V.; Rudic, S.; Mays, T.J. Direct Evidence for Solid-like Hydrogen in a Nanoporous Carbon Hydrogen Storage Material at Supercritical Temperatures. ACS Nano 2015, 9, 8249–8254. [Google Scholar] [CrossRef] [Green Version]
  30. Loloie, Z.; Mozaffarian, M.; Soleimani, M.; Asassian, N. Carbonization and CO2 activation of scrap tires: Optimization of specific surface area by the Taguchi method. Korean J. Chem. Eng. 2017, 34, 366–375. [Google Scholar] [CrossRef]
  31. Sumathi, S.; Bhatia, S.; Lee, K.T.; Mohamed, A.R. Optimization of microporous palm shell activated carbon production for flue gas desulphurization: Experimental and statistical studies. Bioresour. Technol. 2009, 100, 1614–1621. [Google Scholar] [CrossRef]
  32. Jia, Q.; Lua, A.C. Effects of pyrolysis conditions on the physical characteristics of oil-palm-shell activated carbons used in aqueous phase phenol adsorption. J. Anal. Appl. Pyrolysis 2008, 83, 175–179. [Google Scholar] [CrossRef]
  33. Lua, A.C.; Lau, F.Y.; Guo, J. Influence of pyrolysis conditions on pore development of oil-palm-shell activated carbons. J. Anal. Appl. Pyrolysis 2006, 76, 96–102. [Google Scholar] [CrossRef]
  34. Bouchelta, C.; Medjram, M.S.; Bertrand, O.; Bellat, J.P. Preparation and characterization of activated carbon from date stones by physical activation with steam. J. Anal. Appl. Pyrolysis 2008, 82, 70–77. [Google Scholar] [CrossRef]
  35. Eriksson, L.; Johansson, E.; Kettaneh-Wold, N.; Wikström, C.; Wold, S. Design of Experiments: Principles and Applications; UMetrics AB: Umeå, Sweden, 2000. [Google Scholar]
  36. Montgomery, D.C. Design and Analysis of Experiments, 7th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
  37. Wahid, Z.; Nadir, N. Improvement of one factor at a time through design of experiments. World Appl. Sci. J. 2013, 21, 56–61. [Google Scholar]
  38. Czitrom, V. One-factor-at-a-time versus designed experiments. Am. Stat. 1999, 53, 126–131. [Google Scholar] [CrossRef]
  39. Baçaoui, A.; Dahbi, A.; Yaacoubi, A.; Bennouna, C.; Maldonado-Hódar, F.; Rivera-Utrilla, J.; Carrasco-Marín, F.; Moreno-Castilla, C. Experimental Design To Optimize Preparation of Activated Carbons for Use in Water Treatment. Environ. Sci. Technol. 2002, 36, 3844–3849. [Google Scholar] [CrossRef]
  40. Zhao, W.; Fierro, V.; Zlotea, C.; Aylon, E.; Izquierdo, M.T.; Latroche, M.; Celzard, A. Optimization of activated carbons for hydrogen storage. Int. J. Hydrog. Energy 2011, 36, 11746–11751. [Google Scholar] [CrossRef]
  41. Mussatto, S.; Fernandes, M.; Rocha, G. Production, characterization and application of activated carbon from brewer’s spent grain lignin. Bioresour. Technol. 2010, 101, 2450–2457. [Google Scholar] [CrossRef] [Green Version]
  42. Cheng, F.; Liang, J.; Zhao, J.; Tao, Z.; Chen, J. Biomass waste-derived microporous carbons with controlled texture and enhanced hydrogen uptake. Chem. Mater. 2008, 20, 1889–1895. [Google Scholar] [CrossRef]
  43. Nor, N.M.; Lau, L.C.; Lee, K.T.; Mohamed, A.R. Synthesis of activated carbon from lignocellulosic biomass and its applications in air pollution control—A review. J. Environ. Chem. Eng. 2013, 1, 658–666. [Google Scholar] [CrossRef]
  44. Daud, W.M.; Ali, W.S. Comparison on pore development of activated carbon produced from palm shell and coconut shell. Bioresour. Technol. 2004, 93, 63–69. [Google Scholar] [CrossRef]
  45. Laudisio, G.; Dash, R.K.; Singer, J.P.; Yushin, G.; Gogotsi, Y.; Fischer, J.E. Carbide-Derived Carbons: A Comparative Study of Porosity Based on Small-Angle Scattering and Adsorption Isotherms. Langmuir 2006, 22, 8945–8950. [Google Scholar] [CrossRef] [PubMed]
  46. Dash, R.; Chmiola, J.; Yushin, G.; Gogotsi, Y.; Laudisio, G.; Singer, J.; Fischer, J.; Kucheyev, S. Titanium carbide derived nanoporous carbon for energy-related applications. Carbon 2006, 44, 2489–2497. [Google Scholar] [CrossRef] [Green Version]
  47. Yeon, S.H.; Osswald, S.; Gogotsi, Y.; Singer, J.P.; Simmons, J.M.; Fischer, J.E.; Lillo-Ródenas, M.A.; Linares-Solano, Á. Enhanced methane storage of chemically and physically activated carbide-derived carbon. J. Power Sources 2009, 191, 560–567. [Google Scholar] [CrossRef]
  48. ISO. Pore Size Distribution and Porosity of Solid Materials by Mercury Porosimetry and Gas Adsorption—Part 3: Analysis of micropores by Gas Adsorption; 2007; ISO 15901-3:2007. Available online: https://www.iso.org/standard/40364.html (accessed on 6 December 2019).
  49. Quantachrome. Powder Tech Note 35: Micropore Size Analysis of Porous Carbons, (n.d.) 1–4. Available online: https://www.quantachrome.com/technotes.html (accessed on 3 October 2017).
  50. ISO. Determination of the specific Surface Area of Solids by Gas Adsorption: BET Method; 2010; ISO 9277: 2010. Available online: https://www.iso.org/standard/44941.html (accessed on 6 December 2019).
  51. Konarev, P.V.; Volkov, V.V.; Sokolova, A.V.; Koch, M.H.J.; Svergun, D.I. PRIMUS: A Windows PC-based system for small-angle scattering data analysis. J. Appl. Crystallogr. 2003, 36, 1277–1282. [Google Scholar] [CrossRef]
  52. Putnam, C.D.; Hammel, M.; Hura, G.L.; Tainer, J.A. X-Ray Scattering (SAXS) Combined with Crystallography and Computation: Defining Accurate Macromolecular Structures, Conformations and Assemblies in Solution. Biophys. J. 2011. [Google Scholar] [CrossRef] [PubMed]
  53. Schnablegger, H.; Singh, Y. The SAXS Guide: Getting Acquainted with the Principles; Anton Paar GmbH: Graz, Austria, 2011. [Google Scholar]
  54. Kalliat, M.; Kwak, C.Y.; Schmidt, P.W. Small-Angle X-Ray Investigation of the Porosity in Coals. In New Approaches Coal Chemistry; American Chemical Society: Washington, DC, USA, 1981; pp. 3–22. [Google Scholar] [CrossRef] [Green Version]
  55. Gibaud, A.; Xue, J.S.; Dahn, J.R. A small angle X-ray scattering study of carbons made from pyrolyzed sugar. Carbon 1996, 34, 499–503. [Google Scholar] [CrossRef]
  56. Rowlandson, J.L.; Woodman, T.J.; Tennison, S.R.; Edler, K.J.; Ting, V.P. Influence of Aromatic Structure on the Thermal Behaviour of Lignin. Waste Biomass Valori. 2018, 1–14. [Google Scholar] [CrossRef] [Green Version]
  57. Ergun, S. Kinetics of the reaction of carbon with carbon dioxide. J. Phys. Chem. 1956, 60, 480–485. [Google Scholar] [CrossRef]
  58. Teng, H.; Lin, H. Activated carbon production from low ash subbituminous coal with CO2 activation. AIChE J. 1998, 44, 1170–1177. [Google Scholar] [CrossRef]
  59. Yang, T.; Lua, A.C. Characteristics of activated carbons prepared from pistachio-nut shells by physical activation. J. Colloid Interface Sci. 2003, 267, 408–417. [Google Scholar] [CrossRef]
  60. Zhang, T.; Walawender, W.P.; Fan, L.T.; Fan, M.; Daugaard, D.; Brown, R.C. Preparation of activated carbon from forest and agricultural residues through CO2 activation. Chem. Eng. J. 2004, 105, 53–59. [Google Scholar] [CrossRef]
  61. Gañán, J.; González, J.F.; González-García, C.M.; Ramiro, A.; Sabio, E.; Román, S. Air-activated carbons from almond tree pruning: Preparation and characterization. Appl. Surf. Sci. 2006, 252, 5988–5992. [Google Scholar] [CrossRef]
  62. Rodríguez-Mirasol, J.; Cordero, T.; Rodríguez, J.J. Preparation and characterization of activated carbons from eucalyptus kraft lignin. Carbon 1993, 31, 87–95. [Google Scholar] [CrossRef]
  63. Lua, A.C.; Yang, T.; Guo, J. Effects of pyrolysis conditions on the properties of activated carbons prepared from pistachio-nut shells. J. Anal. Appl. Pyrolysis 2004, 72, 279–287. [Google Scholar] [CrossRef]
  64. Guo, J.; Lua, A.C. Characterization of chars pyrolyzed from oil palm stones for the preparation of activated carbons. J. Anal. Appl. Pyrolysis 1998, 46, 113–125. [Google Scholar] [CrossRef]
  65. Daud, W.M.; Ali, W.S.; Sulaiman, M.Z. Effects of carbonization temperature on pore development in palm-shell-based activated carbon. Carbon 2000, 38, 1925–1932. [Google Scholar] [CrossRef]
  66. Rodriguez-Reinoso, F. Controlled Gasification of Carbon and Pore Structure Development. In Fundamental Issues in Control of Carbon Gasification Reactivity; Springer: Dordrecht, The Netherlands, 1991; pp. 533–571. [Google Scholar] [CrossRef]
  67. Baklanova, O.N.; Plaksin, G.V.; Drozdov, V.A.; Duplyakin, V.K.; Chesnokov, N.V.; Kuznetsov, B.N. Preparation of microporous sorbents from cedar nutshells and hydrolytic lignin. Carbon 2003, 41, 1793–1800. [Google Scholar] [CrossRef]
  68. Ismailova, M.G. Influence of the carbonization conditions on the formation of the porous structure of activated carbon from cotton lignin. Prot. Met. Phys. Chem. Surf. 2009, 45, 212–215. [Google Scholar] [CrossRef]
  69. Rodriguez-Mirasol, J.; Cordero, T.; Rodriguez, J.J. Activated carbons from carbon dioxide partial gasification of eucalyptus kraft lignin. Energy Fuels 1993, 7, 133–138. [Google Scholar] [CrossRef]
  70. Fu, K.; Yue, Q.; Gao, B.; Sun, Y.; Zhu, L. Preparation, characterization and application of lignin-based activated carbon from black liquor lignin by steam activation. Chem. Eng. J. 2013, 228, 1074–1082. [Google Scholar] [CrossRef]
  71. Carrott, P.J.M.; Carrott, M.R.; Guerrero, C.I.; Delgado, L.A. Reactivity and porosity development during pyrolysis and physical activation in CO2 or steam of kraft and hydrolytic lignins. J. Anal. Appl. Pyrolysis 2008, 82, 264–271. [Google Scholar] [CrossRef] [Green Version]
  72. Bimbo, N.; Ting, V.P.; Sharpe, J.E.; Mays, T.J. Analysis of optimal conditions for adsorptive hydrogen storage in microporous solids. Colloids Surf. A Physicochem. Eng. Asp. 2013, 437, 113–119. [Google Scholar] [CrossRef]
  73. Hruzewicz-Kołodziejczyk, A.; Ting, V.P.; Bimbo, N.; Mays, T.J. Improving comparability of hydrogen storage capacities of nanoporous materials. Int. J. Hydrog. Energy 2012, 37, 2728–2736. [Google Scholar] [CrossRef]
  74. Armandi, M.; Bonelli, B.; Geobaldo, F.; Garrone, E. Nanoporous carbon materials obtained by sucrose carbonization in the presence of KOH. Microporous Mesoporous Mater. 2010, 132, 414–420. [Google Scholar] [CrossRef]
  75. Sevilla, M.; Fuertes, A.B.; Mokaya, R. High density hydrogen storage in superactivated carbons from hydrothermally carbonized renewable organic materials. Energy Environ. Sci. 2011, 4, 1400–1410. [Google Scholar] [CrossRef] [Green Version]
  76. Zhang, K.; Zhang, Y.; Wang, S. Enhancing thermoelectric properties of organic composites through hierarchical nanostructures. Sci. Rep. 2013, 3, 3448. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  77. Balathanigaimani, M.S.; Shim, W.-G.; Kim, T.-H.; Cho, S.-J.; Lee, J.-W.; Moon, H. Hydrogen storage on highly porous novel corn grain-based carbon monoliths. Catal. Today 2009, 146, 234–240. [Google Scholar] [CrossRef]
  78. Heo, Y.-J.; Park, S.-J. Synthesis of activated carbon derived from rice husks for improving hydrogen storage capacity. J. Ind. Eng. Chem. 2015, 31, 330–334. [Google Scholar] [CrossRef]
  79. Yushin, G.; Dash, R.; Jagiello, J.; Fischer, J.E.; Gogotsi, Y. Carbide-derived carbons: Effect of pore size on hydrogen uptake and heat of adsorption. Adv. Funct. Mater. 2006, 16, 2288–2293. [Google Scholar] [CrossRef]
Carbon 05 00082 g001 550
Figure 1. Regression coefficient plots indicating the influence of carbonisation temperature (CTemp), activation temperature (ATemp), and activation time (ATime) on (a) activated carbon BET surface area, (b) SAXS-derived average pore size, and (c) H2 uptake at 77 K and 1 bar. The refined models are displayed here, with the insignificant factors removed as necessary to maximise the model validity. Error bars represent the 95% confidence interval.
Figure 1. Regression coefficient plots indicating the influence of carbonisation temperature (CTemp), activation temperature (ATemp), and activation time (ATime) on (a) activated carbon BET surface area, (b) SAXS-derived average pore size, and (c) H2 uptake at 77 K and 1 bar. The refined models are displayed here, with the insignificant factors removed as necessary to maximise the model validity. Error bars represent the 95% confidence interval.
Carbon 05 00082 g001
Carbon 05 00082 g002 550
Figure 2. Carbon dioxide isotherms recorded at 273 K on lignin chars carbonised at 350 °C or 900 °C for 30 min. The adsorption branch is indicated by closed symbols and the desorption branch by open symbols.
Figure 2. Carbon dioxide isotherms recorded at 273 K on lignin chars carbonised at 350 °C or 900 °C for 30 min. The adsorption branch is indicated by closed symbols and the desorption branch by open symbols.
Carbon 05 00082 g002
Carbon 05 00082 g003 550
Figure 3. Response surface plot showing the influence of carbonisation and activation temperature and activation dwell time on activated carbon BET surface area. Carbonisation dwell time is held fixed at its highest level (360 min).
Figure 3. Response surface plot showing the influence of carbonisation and activation temperature and activation dwell time on activated carbon BET surface area. Carbonisation dwell time is held fixed at its highest level (360 min).
Carbon 05 00082 g003
Carbon 05 00082 g004 550
Figure 4. Response surface contour plot for activated carbon average pore size, showing the influence of carbonisation and activation temperature. Carbonisation and activation dwell time are held fixed at their highest levels (360 min and 60 min respectively).
Figure 4. Response surface contour plot for activated carbon average pore size, showing the influence of carbonisation and activation temperature. Carbonisation and activation dwell time are held fixed at their highest levels (360 min and 60 min respectively).
Carbon 05 00082 g004
Carbon 05 00082 g005 550
Figure 5. Surface plot predicting how the normalised BET surface area (284–1409 m2 g−1), average pore width (7.7–10.0 Å), and H2 uptake at 77 K (1.2–2.0 wt.%) responses vary with activation temperature (ATemp) and carbonisation temperature (CTemp); carbonisation and activation dwell time were held at their maximum values, 360 min and 60 min, respectively. The plot was created with the software MODDE Pro Version 11.0.2.2309.
Figure 5. Surface plot predicting how the normalised BET surface area (284–1409 m2 g−1), average pore width (7.7–10.0 Å), and H2 uptake at 77 K (1.2–2.0 wt.%) responses vary with activation temperature (ATemp) and carbonisation temperature (CTemp); carbonisation and activation dwell time were held at their maximum values, 360 min and 60 min, respectively. The plot was created with the software MODDE Pro Version 11.0.2.2309.
Carbon 05 00082 g005
Carbon 05 00082 g006 550
Figure 6. A plot of experimentally observed points against those predicted by regression analysis (dotted line) for each activated carbon response; BET surface area, SAXS-derived pore size and H2 uptake at 77 K. The points are labelled with the corresponding experiment numbers, which are listed in Table 2. The summary of fit parameters R2 and Q2 for each plot are listed in Table 3.
Figure 6. A plot of experimentally observed points against those predicted by regression analysis (dotted line) for each activated carbon response; BET surface area, SAXS-derived pore size and H2 uptake at 77 K. The points are labelled with the corresponding experiment numbers, which are listed in Table 2. The summary of fit parameters R2 and Q2 for each plot are listed in Table 3.
Carbon 05 00082 g006
Carbon 05 00082 g007 550
Figure 7. Adsorptive properties derived from nitrogen adsorption isotherms collected at 77 K up to 1 bar for lignin-derived activated carbons (LACs) pyrolysed at 350 °C for 30 min (Exp. 5) or 900 °C for 360 min (Exp. 8) then activated at 1000 °C for 60 min. (a) Radar chart showing the maximum quantity of nitrogen adsorbed (Max Qads), the total (Vtot) and micropore (Vmicro) pore volumes; the BET (SBET) and micropore (Smicro) surface areas; and the volume-weighted average pore size (wavg: GSA) derived from (b) the pore size distribution, which was calculated by fitting of the 2D-NLDFT model.
Figure 7. Adsorptive properties derived from nitrogen adsorption isotherms collected at 77 K up to 1 bar for lignin-derived activated carbons (LACs) pyrolysed at 350 °C for 30 min (Exp. 5) or 900 °C for 360 min (Exp. 8) then activated at 1000 °C for 60 min. (a) Radar chart showing the maximum quantity of nitrogen adsorbed (Max Qads), the total (Vtot) and micropore (Vmicro) pore volumes; the BET (SBET) and micropore (Smicro) surface areas; and the volume-weighted average pore size (wavg: GSA) derived from (b) the pore size distribution, which was calculated by fitting of the 2D-NLDFT model.
Carbon 05 00082 g007
Carbon 05 00082 g008 550
Figure 8. (a) Hydrogen isotherms showing gravimetric uptake at 77 K up to 1 bar in activated carbons from this work (Exp. 5 and Exp. 8). The industrially produced activated carbon TE7 is included for comparison. Symbols are filled for the adsorption branch and empty for the desorption branch. (b) Hydrogen uptake at 1 bar and 77 K as a function of BET surface area for the lignin carbons in this work (Exp. 5 and Exp. 8), TE7, and carbons previously reported in the literature: biomass-derived carbons from physical activation (data from [21,22,23]) biomass-derived carbons from chemical activation (data from [12,13,22,74,75,76,77,78]) other lignin-derived carbons from chemical or physical activation (data from [39,42]) carbide-derived carbons (data from [79]) and activated carbide-derived carbons (data from [79]). The x and y error bars represent the standard deviation between repeat BET surface area and H2 uptake measurements, respectively.
Figure 8. (a) Hydrogen isotherms showing gravimetric uptake at 77 K up to 1 bar in activated carbons from this work (Exp. 5 and Exp. 8). The industrially produced activated carbon TE7 is included for comparison. Symbols are filled for the adsorption branch and empty for the desorption branch. (b) Hydrogen uptake at 1 bar and 77 K as a function of BET surface area for the lignin carbons in this work (Exp. 5 and Exp. 8), TE7, and carbons previously reported in the literature: biomass-derived carbons from physical activation (data from [21,22,23]) biomass-derived carbons from chemical activation (data from [12,13,22,74,75,76,77,78]) other lignin-derived carbons from chemical or physical activation (data from [39,42]) carbide-derived carbons (data from [79]) and activated carbide-derived carbons (data from [79]). The x and y error bars represent the standard deviation between repeat BET surface area and H2 uptake measurements, respectively.
Carbon 05 00082 g008
Table
Table 1. The factors under investigation, their abbreviations and the levels studied.
Table 1. The factors under investigation, their abbreviations and the levels studied.
FactorFactor AbbreviationLow LevelCorresponding Low ValueHigh LevelCorresponding High ValueMid-PointCorresponding Mid-Point Value
Carbonisation temperatureCTemp−1350 °C+1900 °C0625 °C
Carbonisation dwell timeCTime−130 min+1360 min0195 min
Activation temperatureATemp−1800 °C+11000 °C0900 °C
Activation dwell timeATime−120 min+160 min040 min
Table
Table 2. Experimental design matrix with the four factors studied: carbonisation temperature (CTemp), carbonisation dwell time (CTime), activation temperature (ATemp) and activation dwell time (ATime). The responses measured were the Brunauer–Emmett–Teller (BET) surface area (SBET), average pore width (wavg: SAXS), and hydrogen uptake at 77 K up to 1 bar. For pore width, the radius of gyration (Rg) was calculated by fitting of the Gibaud model to small-angle x-ray scattering (SAXS) patterns then converted to pore radius using the relation: w avg =   ( 5 / 3 ) 1 / 2 R g .
Table 2. Experimental design matrix with the four factors studied: carbonisation temperature (CTemp), carbonisation dwell time (CTime), activation temperature (ATemp) and activation dwell time (ATime). The responses measured were the Brunauer–Emmett–Teller (BET) surface area (SBET), average pore width (wavg: SAXS), and hydrogen uptake at 77 K up to 1 bar. For pore width, the radius of gyration (Rg) was calculated by fitting of the Gibaud model to small-angle x-ray scattering (SAXS) patterns then converted to pore radius using the relation: w avg =   ( 5 / 3 ) 1 / 2 R g .
Experiment Number (Exp)Experimental ParametersResponse Parameters
CarbonisationActivationSBET (m2 g−1)wavg: SAXS (Å)H2 Uptake (wt.%)
CTemp (°C)CTime (min)ATemp (°C)ATime (min)
135030800204867.71.20
290030800604329.11.18
3350360800605368.11.24
4900360800202849.41.16
53503010006014099.31.93
6900301000205969.21.39
73503601000206849.11.48
8900360100060105510.01.61
9625195900405128.61.28
10625195900405188.71.29
11625195900405028.41.29
Table
Table 3. Analysis of variance (ANOVA) of the responses measured for lignin-derived activated carbons.
Table 3. Analysis of variance (ANOVA) of the responses measured for lignin-derived activated carbons.
ResponseR2Q2p-Value
BET Surface Area 0.940.81<0.010.01
Average Pore Size0.880.650.010.17
H2 Uptake0.880.790.01>0.01

Share and Cite

MDPI and ACS Style

Rowlandson, J.L.; Coombs OBrien, J.; Edler, K.J.; Tian, M.; Ting, V.P. Application of Experimental Design to Hydrogen Storage: Optimisation of Lignin-Derived Carbons. C 2019, 5, 82. https://doi.org/10.3390/c5040082

AMA Style

Rowlandson JL, Coombs OBrien J, Edler KJ, Tian M, Ting VP. Application of Experimental Design to Hydrogen Storage: Optimisation of Lignin-Derived Carbons. C. 2019; 5(4):82. https://doi.org/10.3390/c5040082

Chicago/Turabian Style

Rowlandson, Jemma L., James Coombs OBrien, Karen J. Edler, Mi Tian, and Valeska P. Ting. 2019. "Application of Experimental Design to Hydrogen Storage: Optimisation of Lignin-Derived Carbons" C 5, no. 4: 82. https://doi.org/10.3390/c5040082

APA Style

Rowlandson, J. L., Coombs OBrien, J., Edler, K. J., Tian, M., & Ting, V. P. (2019). Application of Experimental Design to Hydrogen Storage: Optimisation of Lignin-Derived Carbons. C, 5(4), 82. https://doi.org/10.3390/c5040082

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop