Pulling Simulations and Hydrogen Sorption Modelling on Carbon Nanotube Bundles
Abstract
:1. Introduction
2. Materials and Methods
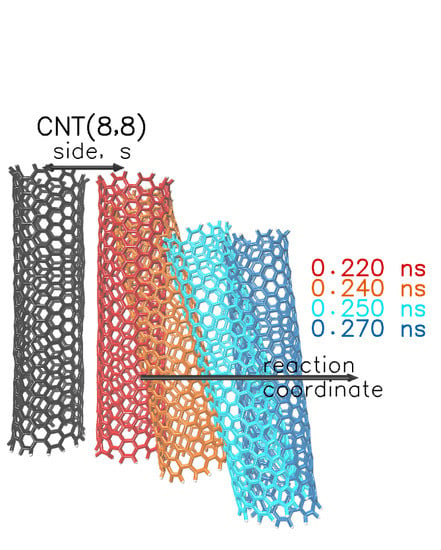
3. Results
| Diameter | Diameter (eff.) | Side | Width | Height | |
|---|---|---|---|---|---|
| CNT(5,5) | 0.678 | 0.338 | 0.963 | 0.991 | 1.249 |
| CNT(6,6) | 0.814 | 0.474 | 1.106 | 1.103 | 1.399 |
| CNT(7,7) | 0.949 | 0.609 | 1.180 | 1.095 | 1.411 |
| CNT(8,8) | 1.085 | 0.745 | 1.372 | 1.291 | 1.658 |
| CNT(9,9) | 1.221 | 0.881 | 1.485 | 1.352 | 1.750 |
| CNT(10,10) | 1.356 | 1.016 | 1.595 | 1.407 | 1.835 |
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zou, C.; Zhao, Q.; Zhang, G.; Xiong, B. Energy revolution: From a fossil energy era to a new energy era. Nat. Gas Ind. 2016, 3, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Ritchie, M.; Roser, M. “Energy”. Published online at OurWorldInData.org. Available online: https://ourworldindata.org/energy (accessed on 1 August 2018).
- Zhou, L. Progress and problems in hydrogen storage methods. Renew. Sustain. Energy Rev. 2005, 9, 395–408. [Google Scholar] [CrossRef]
- Zuttel, A. Materials for hydrogen storage. Mater. Today 2003, 6, 24–33. [Google Scholar] [CrossRef]
- Thomas, K.M. Hydrogen adsorption and storage on porous materials. Catal. Today 2007, 120, 389–398. [Google Scholar] [CrossRef]
- Rivard, E.; Trudeau, M.; Zaghib, K. Hydrogen Storage for Mobility: A Review. Materials 2019, 12, 1973. [Google Scholar] [CrossRef] [Green Version]
- Züttel, A.A.; Wenger, P.; Rentsch, S.; Sudan, P.; Mauron, P.H.; Emmenegger, C.H. LiBH4 a new hydrogen storage material. J. Power Sources 2003, 118, 1–7. [Google Scholar] [CrossRef]
- Sakintuna, B.; Lamari-Darkrim, F.; Hirscher, M. Metal hydride materials for solid hydrogen storage: A review. Int. J. Hydrogen Energy 2007, 32, 1121–1140. [Google Scholar] [CrossRef]
- Hirscher, M.; Yartys, V.A.; Baricco, M.; Bellosta von Colbe, J.; Blanchard, D.; Bowman, R.C.; Broom, D.P.; Buckley, C.E.; Chang, F.; Chen, P.; et al. Materials for hydrogen-based energy storage—Past, recent progress and future outlook. J. Alloy. Compd. 2019, 827, 153548. [Google Scholar] [CrossRef]
- Sherif, S.A.; Zeytinoglu, N.; Veziroglu, T.N. Liquid hydrogen: Potential, problems and a proposed research program. Int. J. Hydrogen Energy 1997, 22, 683–688. [Google Scholar] [CrossRef]
- Felderhoff, M.; Weidenthaler, C.; von Helmolt, R.; Eberle, U. Hydrogen storage: The remaining scientific and technological challenges. Phys. Chem. Chem. Phys. 2007, 9, 2643–2653. [Google Scholar] [CrossRef] [PubMed]
- Broom, D.P. Hydrogen storage materials. In The Characterisation of Their Storage Properties; Springer: London, UK, 2011; ISBN 9780857292116. [Google Scholar]
- Becher, M.; Haluska, M.; Hirscher, M.; Quintel, A.; Skakalova, V.; Dettlaff-Weglikovska, U.; Chen, X.; Hulman, M.; Choi, Y.; Roth, S.; et al. Hydrogen storage in carbon nanotubes. C. R. Phys. 2003, 4, 1055–1062. [Google Scholar] [CrossRef]
- Petrushenko, I.K.; Petrushenko, K.B. Physical adsorption of hydrogen molecules on single-walled carbon nanotubes and carbon-boron-nitrogen heteronanotubes: A comparative DFT study. Vacuum 2019, 167, 280–286. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, J.; Liu, Y.; Zheng, Q. Adsorption equilibrium of hydrogen adsorption on activated carbon, multi-walled carbon nanotubes and graphene sheets. Cryogenics 2019, 101, 36–42. [Google Scholar] [CrossRef]
- Kovalev, V.; Yakunchikov, A.; Li, F. pH-sensitive loading/releasing of doxorubicin using single-walled carbon nanotube and multi-walled carbon nanotube: A molecular dynamics study. Acta Astronaut. 2011, 68, 681–685. [Google Scholar] [CrossRef]
- Brzhezinskaya, M.; Belenkov, E.A.; Greshnyakov, V.A.; Yalovega, G.E.; Bashkin, I.O. New aspects in the study of carbon-hydrogen interaction in hydrogenated carbon nanotubes for energy storage applications. J. Alloy. Compd. 2019, 792, 713–720. [Google Scholar] [CrossRef]
- Dündar-Tekkaya, E.; Karatepe, N. Hydrogen adsorption of carbon nanotubes grown on different catalysts. Int. J. Hydrogen Energy 2015, 40, 7665–7670. [Google Scholar] [CrossRef]
- Gromov, S.V.; Burmistrov, I.N.; Ilinykh, I.A.; Kuznetsov, D.V. Simulation of hydrogen adsorption on carbon nanotubes with different chirality parameters. IOP Conf. Ser. Mater. Sci. Eng. 2016, 112, 12006. [Google Scholar] [CrossRef] [Green Version]
- Maleki, R.; Afrouzi, H.H.; Hosseini, M.; Toghraie, D.; Piranfar, A.; Rostami, S. Simulation of hydrogen adsorption in carbon nanotube arrays. Comput. Methods Programs Biomed. 2020, 186, 105210. [Google Scholar] [CrossRef]
- Shkolin, A.V.; Fomkin, A.A.; Yakovlev, V.Y.; Men’shchikov, I.E. Model Nanoporous Supramolecular Structures Based on Carbon Nanotubes and Hydrocarbons for Methane and Hydrogen Adsorption. Colloid J. 2018, 80, 739–750. [Google Scholar] [CrossRef]
- Varshoy, S.; Khoshnevisan, B.; Mohsen Behpour, M. Enhanced hydrogen storage capacity of Ni/Sn-coated MWCNT nanocomposites. Nanotechnology 2018, 29, 075402. [Google Scholar] [CrossRef]
- Yang, H.; Lombardo, L.; Luo, W.; Kim, W.; Züttel, A. Hydrogen storage properties of various carbon supported NaBH4 prepared via metathesis. Int. J. Hydrogen Energy 2018, 43, 7108–7116. [Google Scholar] [CrossRef]
- Narjes, D.; Heidar, R.; Zohre, H.; Farzaneh, F. Using molecular dynamics simulation to explore the binding of the three potent anticancer drugs sorafenib, streptozotocin, and sunitinib to functionalized carbon nanotubes. J. Mol. Model. 2019, 25, 159. [Google Scholar]
- Tian, M.; Rochat, S.; Polak-Kraśna, K.; Holyfield, L.T.; Burrows, A.D.; Bowen, C.R.; Mays, T.J. Nanoporous polymer-based composites for enhanced hydrogen storage. Adsorption 2019, 25, 889–901. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Mao, D.; Wu, J.; Wang, X.; Wang, Z.; Zhou, G.; Chen, L.; Chen, J.; Zeng, S. Carbon Nanotubes Translocation through a Lipid Membrane and Transporting Small Hydrophobic and Hydrophilic Molecules. Appl. Sci. 2019, 9, 4271. [Google Scholar] [CrossRef] [Green Version]
- Zhan, S.; Ahlquist, M.S. Dynamics and Reactions of Molecular Ru Catalysts at Carbon Nanotube–Water Interfaces. J. Am. Chem. Soc. 2018, 140, 7498–7503. [Google Scholar] [CrossRef]
- Gusain, R.; Kumar, N.; Ray, S.S. Recent advances in carbon nanomaterial-based adsorbents for water purification. Coord. Chem. Rev. 2020, 405, 213111. [Google Scholar] [CrossRef]
- Cracknell, R.F. Simulation of hydrogen adsorption in carbon nanotubes. Mol. Phys. 2002, 100, 2079–2086. [Google Scholar] [CrossRef]
- Darkrim, F.; Levesque, D. High Adsorptive Property of Opened Carbon Nanotubes at 77 K. J. Phys. Chem. 2000, 104, 6773–6776. [Google Scholar] [CrossRef]
- Stan, G.; Cole, M.W. Hydrogen Adsorption in Nanotubes. J. Low Temp. Phys. 1998, 110, 539–544. [Google Scholar] [CrossRef]
- Gotzias, A.; Heiberg-Andersen, H.; Kainourgiakis, M.; Steriotis, T. Grand canonical Monte Carlo simulations of hydrogen adsorption in carbon cones. Appl. Surf. Sci. 2010, 256, 5226–5231. [Google Scholar] [CrossRef]
- Gotzias, A.; Heiberg-Andersen, H.; Kainourgiakis, M.; Steriotis, T. A grand canonical Monte Carlo study of hydrogen adsorption in carbon nanohorns and nanocones at 77K. Carbon 2011, 49, 2715–2724. [Google Scholar] [CrossRef]
- Lemkul, J.A.; Bevan, D.R. Assessing the Stability of Alzheimer’s Amyloid Protofibrils Using Molecular Dynamics. J. Phys. Chem. B 2010, 114, 1652–1660. [Google Scholar] [CrossRef]
- Vijayaraj, R.; Van Damme, S.; Bultinck, P.; Subramanian, V. Molecular Dynamics and Umbrella Sampling Study of Stabilizing Factors in Cyclic Peptide-Based Nanotubes. J. Phys. Chem. B 2012, 116, 9922–9933. [Google Scholar] [CrossRef]
- Nawrocki, G.; Cieplak, M. Amino acids and proteins at ZnO–water interfaces in molecular dynamics simulations. Phys. Chem. Chem. Phys. 2013, 15, 13628–13636. [Google Scholar] [CrossRef] [Green Version]
- Gladich, I.; Habartová, A.; Roeselová, M. Adsorption, Mobility, and Self-Association of Naphthalene and 1-Methylnaphthalene at the Water–Vapor Interface. J. Phys. Chem. A 2018, 118, 1052–1066. [Google Scholar] [CrossRef]
- Hedger, G.; Shorthouse, D.; Koldsø, H.; Sansom, M. Free Energy Landscape of Lipid Interactions with Regulatory Binding Sites on the Transmembrane Domain of the EGF Receptor. J. Phys. Chem. B 2016, 120, 8154–8163. [Google Scholar] [CrossRef]
- Kolman, K.; Abbas, Z. Molecular dynamics exploration for the adsorption of benzoic acid derivatives on charged silica surfaces. Colloids Surf. Physicochem. Eng. Asp. 2019, 578, 123635. [Google Scholar] [CrossRef]
- Chakraborty, S.; Lim, F.C.; Ye, J. Achieving an Optimal Tg Change by Elucidating the Polymer–Nanoparticle Interface: A Molecular Dynamics Simulation Study of the Poly(vinyl alcohol)–Silica Nanocomposite System. J. Phys. Chem. C 2019, 123, 23995–24006. [Google Scholar] [CrossRef]
- Yan, H.; Yuan, S. Molecular Dynamics Simulation of the Oil Detachment Process within Silica Nanopores. J. Phys. Chem. C 2016, 120, 2667–2674. [Google Scholar] [CrossRef]
- Zhou, H.; Yu, H.; Zhao, X.; Yang, L.; Huang, X. Molecular dynamics simulations investigate the pathway of substrate entry active site of rhomboid protease. J. Biomol. Struct. Dyn. 2019, 37, 3445–3455. [Google Scholar] [CrossRef]
- Karozis, S.; Mavroudakis, E.; Charalambopoulou, G.; Kainourgiakis, M. Molecular simulations of self-assembled ceramide bilayers: Comparison of structural and barrier properties. Mol. Simul. 2020, 46, 1–9. [Google Scholar] [CrossRef]
- Bodnarchuk, M.S.; Dini, D.; Heyes, D.M.; Breakspear, A.; Chahine, S. Molecular Dynamics Studies of Overbased Detergents on a Water Surface. Langmuir 2017, 33, 7263–7270. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.; Croy, A.; Bezugly, V.; Cuniberti, G. Molecular Dynamics Studies of Overbased Detergents on a Water Surface. Phys. Chem. Chem. Phys. 2019, 21, 24007–24016. [Google Scholar] [CrossRef] [Green Version]
- Shaoqi, Z.; De Triviño, G.; Angel, J.; Mårten, A. The Carboxylate Ligand as an Oxide Relay in Catalytic Water Oxidation. J. Am. Chem. Soc. 2019, 21, 10247–10252. [Google Scholar]
- Farrokhpour, H.; Mansouri, A.; Rajabi, A.R.; Chermahini, A.N. The effect of the diameter of cyclic peptide nanotube on its chirality discrimination. J. Biomol. Struct. Dyn. 2019, 37, 691–701. [Google Scholar] [CrossRef]
- Vijayakumar, V.; Vijayaraj, R.; Peters, G.H. In silico study of amphiphilic nanotubes based on cyclic peptides in polar and non-polar solvent. J. Mol. Model. 2016, 22, 264. [Google Scholar] [CrossRef]
- Minoia, A.; Guo, Z.; Xu, H.; George, S.J.; Schenning, A.; Feyter, S.; Lazzaroni, R. Assessing the role of chirality in the formation of rosette-like supramolecular assemblies on surfaces. Chem. Commun. 2011, 47, 10924–10926. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Gotzias, A.; Kouvelos, E.; Sapalidis, A. Computing the temperature dependence of adsorption selectivity in porous solids. Surf. Coat. Technol. 2018, 350, 95–100. [Google Scholar] [CrossRef]
- Gotzias, A. Calculating adsorption isotherms using Lennard Jones particle density distributions. J. Phys. Condens. Matter 2019, 31, 435901. [Google Scholar] [CrossRef] [PubMed]
- Düren, T.; Millange, F.; Férey, G.; Walton, K.S.; Snurr, R.Q. Calculating Geometric Surface Areas as a Characterization Tool for Metal Organic Frameworks. J. Phys. Chem. C 2007, 111, 15350–15356. [Google Scholar] [CrossRef]
- Sarkisov, L.; Harrison, A. Computational structure characterisation tools in application to ordered and disordered porous materials. Mol. Simul. 2011, 37, 1248–1257. [Google Scholar] [CrossRef]
- Miklitz, M.; Jelfs, K. pywindow: Automated Structural Analysis of Molecular Pores. J. Chem. Inf. Model. 2018, 58, 2387–2391. [Google Scholar] [CrossRef]
- Lacomi, P.; Llewellyn, P. pyGAPS: A Python-based framework for adsorption isotherm processing and material characterisation. Adsorption 2019, 25, 1533–1542. [Google Scholar]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications; Academic: New York, NY, USA, 1996. [Google Scholar]
- Cousins, K.; Zhang, R. Highly Porous Organic Polymers for Hydrogen Fuel Storage. Polymers 2019, 11, 690. [Google Scholar] [CrossRef] [Green Version]
- Tanaka, H.; Kanoh, H.; Yudasaka, M.; Iijima, S.; Kaneko, K. Quantum Effects on Hydrogen Isotope Adsorption on Single-Wall Carbon Nanohorns. J. Am. Chem. Soc. 2005, 127, 7511–7516. [Google Scholar] [CrossRef]
- Gotzias, A.; Steriotis, T. D2/H2 quantum sieving in microporous carbons: A theoretical study on the effects of pore size and pressure. Mol. Phys. 2012, 110, 1179–1187. [Google Scholar] [CrossRef]
- Gotzias, A.; Charalambopoulou, G.; Ampoumogli, A.; Krkljus, I.; Hirscher, M.; Steriotis, T. Experimental and theoretical study of D2/H2 quantum sieving in a carbon molecular sieve. Adsorption 2013, 19, 373–379. [Google Scholar] [CrossRef]
- Krkljus, I.; Steriotis, T.; Charalambopoulou, G.; Gotzias, A.; Hirscher, M. H2/D2 adsorption and desorption studies on carbon molecular sieves with different pore structures. Carbon 2013, 57, 239–247. [Google Scholar] [CrossRef]





| Total (Helium) Pore Volume (cm/g) | Change (% from Triangular) | ||||
|---|---|---|---|---|---|
| Triangular | Intermediate | Honeycomb | Intermediate | Honeycomb | |
| CNT(5,5) | 1.37 | 1.67 | 2.08 | 22.3 | 52.2 |
| CNT(6,6) | 1.52 | 1.85 | 2.27 | 21.7 | 49.7 |
| CNT(7,7) | 1.50 | 1.80 | 2.21 | 20.1 | 47.5 |
| CNY(8,8) | 1.68 | 2.03 | 2.50 | 21.4 | 49.2 |
| CNT(9,9) | 1.73 | 2.10 | 2.58 | 21.1 | 48.6 |
| CNT(10,10) | 1.80 | 2.17 | 2.66 | 20.5 | 47.8 |
| Weight (g/mol) in the Cell | |||
|---|---|---|---|
| Triangular | Intermediate | Honeycomb | |
| CNT(5,5) | 23,800 | 20,400 | 17,000 |
| CNT(6,6) | 28,560 | 24,480 | 20,400 |
| CNT(7,7) | 33,320 | 28,560 | 23,800 |
| CNT(8,8) | 38,080 | 32,640 | 27,200 |
| CNT(9,9) | 42,840 | 36,720 | 30,600 |
| CNT(10,10) | 47,600 | 40,800 | 34,000 |
| Surface Area (m/g) | Change (% from Triangular) | ||||
|---|---|---|---|---|---|
| Triangular | Intermediate | Honeycomb | Intermediate | Honeycomb | |
| CNT(5,5) | 1601.25 | 2081.72 | 2364.15 | 30.0 | 47.6 |
| CNT(6,6) | 1750.66 | 2221.26 | 2522.03 | 26.9 | 44.1 |
| CNT(7,7) | 1874.01 | 2291.26 | 2566.58 | 22.3 | 37.0 |
| CNT(8,8) | 2092.28 | 2609.34 | 2878.45 | 24.7 | 37.6 |
| CNT(9,9) | 2201.74 | 2679.08 | 2937.47 | 21.7 | 33.4 |
| CNT(10,10) | 2262.70 | 2760.00 | 3005.34 | 22.0 | 32.8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gotzias, A.; Sapalidis, A. Pulling Simulations and Hydrogen Sorption Modelling on Carbon Nanotube Bundles. C 2020, 6, 11. https://doi.org/10.3390/c6010011
Gotzias A, Sapalidis A. Pulling Simulations and Hydrogen Sorption Modelling on Carbon Nanotube Bundles. C. 2020; 6(1):11. https://doi.org/10.3390/c6010011
Chicago/Turabian StyleGotzias, Anastasios, and Andreas Sapalidis. 2020. "Pulling Simulations and Hydrogen Sorption Modelling on Carbon Nanotube Bundles" C 6, no. 1: 11. https://doi.org/10.3390/c6010011
APA StyleGotzias, A., & Sapalidis, A. (2020). Pulling Simulations and Hydrogen Sorption Modelling on Carbon Nanotube Bundles. C, 6(1), 11. https://doi.org/10.3390/c6010011