Physi-Sorption of H2 on Pure and Boron–Doped Graphene Monolayers: A Dispersion–Corrected DFT Study
Abstract
:1. Introduction
2. Methods
3. Results
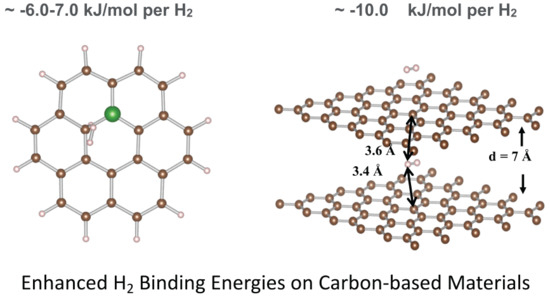
3.1. Coronene Model Calculations
3.1.1. Benchmarking Level of Theory for H2 Binding to Coronene
3.1.2. Effect of Boron Substitution on H2 Binding
3.1.3. Effect of Boron Doping on the Charge Distribution
3.1.4. Effect of Boron Doping on the Bond Order
3.1.5. Other Possibilities for H2 Binding
3.2. Periodic Two–Dimensional and Three–Dimensional Doped Graphene
3.2.1. Benchmarking Level of Theory for H2 Binding on Graphene
3.2.2. Effect of Boron Doping Concentration on H2 Binding
3.2.3. Effect of Interlayer Distance Between Graphene Monolayers on the H2 Binding
4. Discussion and Conclusion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- He, T.; Pachfule, P.; Wu, H.; Xu, Q.; Chen, P. Hydrogen carriers. Nat. Rev. Mater. 2016, 1, 1–7. [Google Scholar] [CrossRef]
- Panella, B.; Hirscher, M.; Roth, S. Hydrogen adsorption in different carbon nanostructures. Carbon 2005, 43, 2209–2214. [Google Scholar] [CrossRef]
- Candelaria, S.L.; Shao, Y.Y.; Zhou, W.; Li, X.L.; Xiao, J.; Zhang, J.G.; Wang, Y.; Liu, J.; Li, J.H.; Cao, G.Z. Nanostructured carbon for energy storage and conversion. Nano Energy 2012, 1, 195–220. [Google Scholar] [CrossRef]
- Yang, J.; Sudik, A.; Wolverton, C.; Siegel, D.J. High capacity hydrogen storage materials: Attributes for automotive applications and techniques for materials discovery. Chem. Soc. Rev. 2010, 39, 656–675. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.C.; Du, Y.; Sun, L.X. Ca-decorated novel boron sheet: A potential hydrogen storage medium. Int J Hydrogen Energy 2016, 41, 5276–5283. [Google Scholar] [CrossRef]
- Cha, M.H.; Nguyen, M.C.; Lee, Y.L.; Im, J.; Ihm, J. Iron-Decorated, Functionalized Metal Organic Framework for High-Capacity Hydrogen Storage: First-Principles Calculations. J. Phys. Chem. C 2010, 114, 14276–14280. [Google Scholar] [CrossRef]
- Kapelewski, M.T.; Runcevski, T.; Tarver, J.D.; Jiang HZ, H.; Hurst, K.E.; Parilla, P.A.; Ayala, A.; Gennett, T.; FitzGerald, S.A.; Brown, C.M.; et al. Record High Hydrogen Storage Capacity in the Metal-Organic Framework Ni-2(m-dobdc) at Near-Ambient Temperatures. Chem. Mater. 2018, 30, 8179–8189. [Google Scholar] [CrossRef]
- Runcevski, T.; Kapelewski, M.T.; Torres-Gavosto, R.M.; Tarver, J.D.; Brown, C.M.; Long, J.R. Adsorption of two gas molecules at a single metal site in a metal-organic framework. Chem. Commun. 2016, 52, 8251–8254. [Google Scholar] [CrossRef]
- McNicholas, T.P.; Wang, A.M.; O’Neill, K.; Anderson, R.J.; Stadie, N.P.; Kleinhammes, A.; Parilla, P.; Simpson, L.; Ahn, C.C.; Wang, Y.Q.; et al. H-2 Storage in Microporous Carbons from PEEK Precursors. J. Phys. Chem. C 2010, 114, 13902–13908. [Google Scholar] [CrossRef] [Green Version]
- Purewal, J.J.; Keith, J.B.; Ahn, C.C.; Fultz, B.; Brown, C.M.; Tyagi, M. Adsorption and melting of hydrogen in potassium-intercalated graphite. Phys. Rev. B 2009, 79, 054305. [Google Scholar] [CrossRef] [Green Version]
- Ahn, C.C.; Ye, Y.; Ratnakumar, B.V.; Witham, C.; Bowman, R.C.; Fultz, B. Hydrogen desorption and adsorption measurements on graphite nanofibers. Appl. Phys. Lett. 1998, 73, 3378–3380. [Google Scholar] [CrossRef]
- Fan, Y.Y.; Liao, B.; Liu, M.; Wei, Y.L.; Lu, M.Q.; Cheng, H.M. Hydrogen uptake in vapor-grown carbon nanofibers. Carbon 1999, 37, 1649–1652. [Google Scholar] [CrossRef]
- Huang, C.W.; Wu, H.C.; Li, Y.Y. Hydrogen storage in platelet graphite nanofibers. Sep. Purif. Technol. 2007, 58, 219–223. [Google Scholar] [CrossRef]
- Browning, D.J.; Gerrard, M.L.; Lakeman, J.B.; Mellor, I.M.; Mortimer, R.J.; Turpin, M.C. Studies into the storage of hydrogen in carbon nanofibers: Proposal of a possible reaction mechanism. Nano Lett. 2002, 2, 201–205. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Johnson, J.K. Molecular simulation of hydrogen adsorption in single-walled carbon nanotubes and idealized carbon slit pores. J. Chem. Phys. 1999, 110, 577–586. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Johnson, J.K. Computer simulations of hydrogen adsorption on graphite nanofibers. J. Phys. Chem. B 1999, 103, 277–281. [Google Scholar] [CrossRef]
- U.S. DRIVE Partnership. Target Explanation Document: Onboard Hydrogen Storage for Light-Duty Fuel Cell Vehicles. 2017. Available online: https://www.energy.gov/sites/prod/files/2017/05/f34/fcto_targets_onboard_hydro_storage_explanation.pdf (accessed on 10 January 2020).
- Kim, Y.H.; Zhao, Y.F.; Williamson, A.; Heben, M.J.; Zhang, S.B. Nondissociative adsorption of H-2 molecules in light-element-doped fullerenes. Phys. Rev. Lett. 2006, 96, 016102. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Z.; Gao, X.P.; Yan, J.; Song, D.Y. Doping effects of B and N on hydrogen adsorption in single-walled carbon nanotubes through density functional calculations. Carbon 2006, 44, 939–947. [Google Scholar] [CrossRef]
- Dai, J.Y.; Yuan, J.M.; Giannozzi, P. Gas adsorption on graphene doped with B, N, Al, and S: A theoretical study. Appl. Phys. Lett. 2009, 95, 232105. [Google Scholar] [CrossRef]
- Sha, X.W.; Cooper, A.C.; Bailey, W.H.; Cheng, H.S. Revisiting Hydrogen Storage in Bulk BC3. J. Phys. Chem. C 2010, 114, 3260–3264. [Google Scholar] [CrossRef]
- Vanin, M.; Mortensen, J.J.; Kelkkanen, A.K.; Garcia-Lastra, J.M.; Thygesen, K.S.; Jacobsen, K.W. Graphene on metals: A van der Waals density functional study. Phys. Rev. B 2010, 81, 081408. [Google Scholar] [CrossRef] [Green Version]
- Dion, M.; Rydberg, H.; Schroder, E.; Langreth, D.C.; Lundqvist, B.I. Van der Waals density functional for general geometries. Phys. Rev. Lett. 2004, 92, 246401. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.; Murray, E.D.; Kong, L.Z.; Lundqvist, B.I.; Langreth, D.C. Higher-accuracy van der Waals density functional. Phys. Rev. B 2010, 82, 081101. [Google Scholar] [CrossRef] [Green Version]
- Klimes, J.; Bowler, D.R.; Michaelides, A. Chemical accuracy for the van der Waals density functional. J Phys. Condens. Mat. 2010, 22, 022201. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.K.; Yang, W.T. Comment on “Generalized gradient approximation made simple”. Phys. Rev. Lett. 1998, 80, 890. [Google Scholar] [CrossRef]
- Varenius, E. Hydrogen Adsorption on Graphene and Coronene A van der Waals Density Functional Study; Chalmers University of Technology: Gothenburg, Sweden, 2011. [Google Scholar]
- Cabria, I.; Lopez, M.J.; Alonso, J.A. Searching for DFT-based methods that include dispersion interactions to calculate the physisorption of H-2 on benzene and graphene. J. Chem. Phys. 2017, 146, 214104. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.F.; Yang, F.H.; Yang, R.T. Hydrogen Storage Properties of B- and N-Doped Microporous Carbon. AIChE J. 2009, 55, 1823–1833. [Google Scholar] [CrossRef] [Green Version]
- Chung, T.M.; Jeong, Y.; Chen, Q.; Kleinhammes, A.; Wu, Y. Synthesis of microporous boron-substituted carbon (B/C) materials using polymeric precursors for hydrogen physisorption. J. Am. Chem. Soc. 2008, 130, 6668–6669. [Google Scholar] [CrossRef]
- Jin, Z.; Sun, Z.Z.; Simpson, L.J.; O’Neill, K.J.; Parilla, P.A.; Li, Y.; Stadie, N.P.; Ahn, C.C.; Kittrell, C.; Tour, J.M. Solution-Phase Synthesis of Heteroatom-Substituted Carbon Scaffolds for Hydrogen Storage. J. Am. Chem. Soc. 2010, 132, 15246–15251. [Google Scholar] [CrossRef] [Green Version]
- Jeong, Y.; Chung, T.M. The synthesis and characterization of a super-activated carbon containing substitutional boron (BCX) and its applications in hydrogen storage. Carbon 2010, 48, 2526–2537. [Google Scholar] [CrossRef]
- Usachov, D.Y.; Fedorov, A.V.; Vilkov, O.Y.; Petukhov, A.E.; Rybkin, A.G.; Ernst, A.; Otrokov, M.M.; Chulkov, E.V.; Ogorodnikov, I.I.; Kuznetsov, M.V.; et al. Large-Scale Sublattice Asymmetry in Pure and Boron-Doped Graphene. Nano Lett. 2016, 16, 4535–4543. [Google Scholar] [CrossRef] [PubMed]
- Shcherban, N.; Filonenko, S.; Yaremov, P.; Dyadyun, V.; Bezverkhyy, I.; Ilyin, V. Boron-doped nanoporous carbons as promising materials for supercapacitors and hydrogen storage. J. Mater. Sci. 2017, 52, 1523–1533. [Google Scholar] [CrossRef]
- Bult, J.B.; Lee, J.; O’Neill, K.; Engtrakul, C.; Hurst, K.E.; Zhao, Y.F.; Simpson, L.J.; Parilla, P.A.; Gennett, T.; Blackburn, J.L. Manipulation of Hydrogen Binding Energy and Desorption Kinetics by Boron Doping of High Surface Area Carbon. J. Phys. Chem. C 2012, 116, 26138–26143. [Google Scholar] [CrossRef]
- Ariharan, A.; Viswanathan, B.; Nandhakumar, V. Hydrogen storage on boron substituted carbon materials. Int. J. Hydrogen Energy 2016, 41, 3527–3536. [Google Scholar] [CrossRef]
- Valiev, M.; Bylaska, E.J.; Govind, N.; Kowalski, K.; Straatsma, T.P.; Van Dam HJ, J.; Wang, D.; Nieplocha, J.; Apra, E.; Windus, T.L.; et al. NWChem: A comprehensive and scalable open-source solution for large scale molecular simulations. Comput. Phys. Commun. 2010, 181, 1477–1489. [Google Scholar] [CrossRef] [Green Version]
- Becke, A.D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic-Behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Lee, C.T.; Yang, W.T.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron-Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [Green Version]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-Consistent Molecular-Orbital Methods.20. Basis Set for Correlated Wave-Functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Hammer, B.; Hansen, L.B.; Norskov, J.K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B 1999, 59, 7413–7421. [Google Scholar] [CrossRef] [Green Version]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Patchkovskii, S.; Tse, J.S.; Yurchenko, S.N.; Zhechkov, L.; Heine, T.; Seifert, G. Graphene nanostructures as tunable storage media for molecular hydrogen. Proc. Natl. Acad. Sci. USA 2005, 102, 10439–10444. [Google Scholar] [CrossRef] [Green Version]
- Camaioni, D.M.; Ginovska-Pangovska, B.; Schenter, G.K.; Kathmann, S.M.; Autrey, T. Analysis of the Activation and Heterolytic Dissociation of H-2 by Frustrated Lewis Pairs: NH3/BX3 (X = H, F, and Cl). J. Phys. Chem. A 2012, 116, 7228–7237. [Google Scholar] [CrossRef]




| System | Binding Energy of H2 | Reference |
|---|---|---|
| Pure Graphene | −5.1 kJ/mol H2 | [2,3] |
| Microporous B/C | −10.8 kJ/mol (0.62 wt %) | [30] |
| B doped Carbon Scaffolds | −8.6 kJ/mol (zero coverage) | [31] |
| Porous BCx | −12 to −20 kJ/mol (high coverage) | [32] |
| B doped CMK-3 | −5 kJ/mol H2 | [34] |
| B doped C | NA | [36] (increased capacity to 5 wt% at 298 K) |
| C36 Fullerenes | −19.2 kJ/mol H2 | [18] * |
| C–Nanotubes | Reduced from −10.3 kJ/mol H2 in pristine | [19] * |
| B doped Graphene | −1.35 kJ/mol H2 | [20] * |
| Pure Coronene | −5.7 kJ/mol H2 | [27] * |
| Pure Graphene | −5.9 kJ/mol H2 | [27] * |
| Pure Graphene | −5.5 kJ/mol H2, −4.6 kJ/mol H2 | [28] * |
| XC Functional | (D3 Corrected) | |
|---|---|---|
| PBE | −0.3 | −9.8 |
| PBE0 | −0.7 | −7.3 |
| B3LYP | 3.1 | −6.2 |
| vdW–DF2 (solid state) [27] | −5.7 | |
| System | Nomenclature | |
|---|---|---|
| C24 H12 | C | −6.2 |
| B C23 H13 | B | −7.6 |
| B2 C22 H12 | BB ortho | −6.6 |
| BB meta | −5.9 | |
| BB para | −5.6 |
| Atom # | C | B | BB ortho | BB meta | BB para |
|---|---|---|---|---|---|
| 1 | 0.10 | 0.01 b | −0.22 | 0.51 b | 0.56 b |
| 2 | 0.06 | −0.28 | 0.13 | −0.22 | −0.21 |
| 3 | 0.06 | 0.11 | 0.13 | 0.16 | −0.12 |
| 4 | 0.11 | 0.09 | −0.27 | −0.22 | 0.37 b |
| 5 | 0.04 | 0.14 | −0.03 b | 0.50 b | −0.19 |
| 6 | 0.05 | −0.54 Cd | −0.03 b | −0.56 | −0.20 |
| Bond Order | C | B | BB ortho | BB meta | BB para |
|---|---|---|---|---|---|
| 1–2 | 1.25 | 1.12 * | 1.24 | 1.01 * | 0.95 * |
| 2–3 | 1.21 | 1.30 | 1.06 | 1.16 | 1.43 |
| 3–4 | 1.25 | 1.14 | 1.25 | 1.17 | 1.00 * |
| 4–5 | 1.26 | 1.30 | 1.04 * | 1.01 * | 1.01 * |
| 5–6 | 1.23 | 1.06 Cd | 1.24 ** | 1.13 * | 1.42 |
| 6–1 | 1.26 | 1.00 *Cd | 1.02 * | 1.13 * | 0.96 * |
| DFT Exchange | Dispersion Method | |
|---|---|---|
| PBE | no dispersion | −0.75 |
| PBE | D3—no damping | −0.8 |
| PBE | D3—Becke-Johnson damping | −0.75 |
| PBE | vdW–DF1 | −9.5 |
| PBE | vdW–DF2 | −6.0 |
| revPBE | vdW–DF2 | −3.8 |
| optPBE | vdW–DF2 | −4.6 |
| RPBE | vdW–DF2 | −5.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nayyar, I.; Ginovska, B.; Karkamkar, A.; Gennett, T.; Autrey, T. Physi-Sorption of H2 on Pure and Boron–Doped Graphene Monolayers: A Dispersion–Corrected DFT Study. C 2020, 6, 15. https://doi.org/10.3390/c6010015
Nayyar I, Ginovska B, Karkamkar A, Gennett T, Autrey T. Physi-Sorption of H2 on Pure and Boron–Doped Graphene Monolayers: A Dispersion–Corrected DFT Study. C. 2020; 6(1):15. https://doi.org/10.3390/c6010015
Chicago/Turabian StyleNayyar, Iffat, Bojana Ginovska, Abhijeet Karkamkar, Thomas Gennett, and Thomas Autrey. 2020. "Physi-Sorption of H2 on Pure and Boron–Doped Graphene Monolayers: A Dispersion–Corrected DFT Study" C 6, no. 1: 15. https://doi.org/10.3390/c6010015
APA StyleNayyar, I., Ginovska, B., Karkamkar, A., Gennett, T., & Autrey, T. (2020). Physi-Sorption of H2 on Pure and Boron–Doped Graphene Monolayers: A Dispersion–Corrected DFT Study. C, 6(1), 15. https://doi.org/10.3390/c6010015