Adsorption of H2 on Penta-Octa-Penta Graphene: Grand Canonical Monte Carlo Study
Abstract
:1. Introduction
2. Methods
3. Structural Models
4. Results
4.1. Interaction Potentials and Potential Fitting
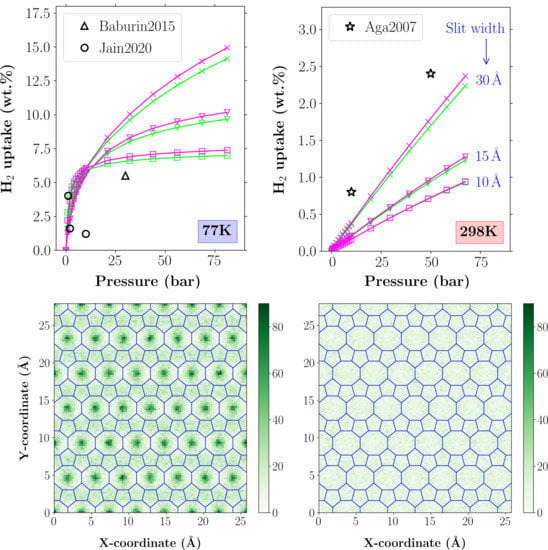
4.2. H Adsorption Properties
4.3. Average H Density Distribution
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kanellopoulos, N. (Ed.) Nanoporous Materials: Advanced Techniques for Characterization, Modeling, and Processing; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Gadipelli, S.; Guo, Z.X. Graphene-based materials: Synthesis and gas sorption, storage and separation. Prog. Mater. Sci. 2015, 69, 1–60. [Google Scholar] [CrossRef] [Green Version]
- Broom, D.; Webb, C.; Fanourgakis, G.; Froudakis, G.; Trikalitis, P.; Hirscher, M. Concepts for improving hydrogen storage in nanoporous materials. Int. J. Hydrog. Energy 2019, 44, 7768–7779. [Google Scholar] [CrossRef]
- Hirscher, M.; Yartys, V.A.; Baricco, M.; von Colbe, J.B.; Blanchard, D.; Bowman, R.C.; Broom, D.P.; Buckley, C.E.; Chang, F.; Chen, P.; et al. Materials for hydrogen-based energy storage—Past, recent progress and future outlook. J. Alloy. Compd. 2019, 827, 153548. [Google Scholar] [CrossRef]
- Steriotis, T.; Charalambopoulou, G.; Stubos, A. Advanced Materials for Hydrogen Storage. In Nanoporous Materials: Advanced Techniques for Characterization, Modeling, and Processing; Kanellopoulos, N., Ed.; CRC Press: Boca Raton, FL, USA, 2011; pp. 513–547. [Google Scholar]
- Kostoglou, N.; Constantinides, G.; Charalambopoulou, G.; Steriotis, T.; Polychronopoulou, K.; Li, Y.; Liao, K.; Ryzhkov, V.; Mitterer, C.; Rebholz, C. Nanoporous spongy graphene: Potential applications for hydrogen adsorption and selective gas separation. Thin Solid Film. 2015, 596, 242–249. [Google Scholar] [CrossRef]
- Kostoglou, N.; Tarat, A.; Walters, I.; Ryzhkov, V.; Tampaxis, C.; Charalambopoulou, G.; Steriotis, T.; Mitterer, C.; Rebholz, C. Few-layer graphene-like flakes derived by plasma treatment: A potential material for hydrogen adsorption and storage. Microporous Mesoporous Mater. 2016, 225, 482–487. [Google Scholar] [CrossRef]
- Kostoglou, N.; Koczwara, C.; Prehal, C.; Terziyska, V.; Babic, B.; Matovic, B.; Constantinides, G.; Tampaxis, C.; Charalambopoulou, G.; Steriotis, T.; et al. Nanoporous activated carbon cloth as a versatile material for hydrogen adsorption, selective gas separation and electrochemical energy storage. Nano Energy 2017, 40, 49–64. [Google Scholar] [CrossRef]
- Kuzubov, A.A.; Popov, M.N.; Fedorov, A.S.; Kozhevnikova, T.A. A theoretical study of the dissociative chemisorption of hydrogen on carbon nanotubes. Russ. J. Phys. Chem. A Focus Chem. 2008, 82, 2117–2121. [Google Scholar] [CrossRef]
- Kuzubov, A.A.; Avramov, R.P.; Raimova, M.A.; Popov, M.N.; Milyutina, Y.M.; Kozhevnikova, T.A.; Artyushenko, P.V. Modeling and calculations of the physicochemical parameters of diffusion of atomic hydrogen on the surface of differently sized nanotubes with different chiralities. Russ. J. Phys. Chem. A 2009, 83, 649–653. [Google Scholar] [CrossRef]
- Dimitrakakis, G.K.; Tylianakis, E.; Froudakis, G.E. Pillared Graphene: A New 3-D Network Nanostructure for Enhanced Hydrogen Storage. Nano Lett. 2008, 8, 3166–3170. [Google Scholar] [CrossRef]
- Ozturk, Z.; Baykasoglu, C.; Kirca, M. Sandwiched graphene-fullerene composite: A novel 3-D nanostructured material for hydrogen storage. Int. J. Hydrog. Energy 2016, 41, 6403–6411. [Google Scholar] [CrossRef]
- Gotzias, A.; Heiberg-Andersen, H.; Kainourgiakis, M.; Steriotis, T. A grand canonical Monte Carlo study of hydrogen adsorption in carbon nanohorns and nanocones at 77K. Carbon 2011, 49, 2715–2724. [Google Scholar] [CrossRef]
- Kuzubov, A.A.; Krasnov, P.O.; Kozhevnikov, T.A.; Popov, M.N. Calculation of the energy of binding of titanium and scandium complexes to the surface of carbon nanotubes. Russ. J. Phys. Chem. B 2009, 3, 679–683. [Google Scholar] [CrossRef]
- Kuzubov, A.A.; Krasnov, P.O.; Kozhevnikova, T.A.; Popov, M.N.; Artyushenko, P.V. Peculiarities of the decoration of carbon nanotubes with transition metal atoms. Russ. J. Phys. Chem. B 2011, 5, 163–167. [Google Scholar] [CrossRef]
- Holec, D.; Kostoglou, N.; Tampaxis, C.; Babic, B.; Mitterer, C.; Rebholz, C. Theory-guided metal-decoration of nanoporous carbon for hydrogen storage applications. Surf. Coatings Technol. 2018, 351, 42–49. [Google Scholar] [CrossRef]
- Wang, S.; Yang, B.; Chen, H.; Ruckenstein, E. Popgraphene: A new 2D planar carbon allotrope composed of 5–8–5 carbon rings for high-performance lithium-ion battery anodes from bottom-up programming. J. Mater. Chem. A 2018, 6, 6815–6821. [Google Scholar] [CrossRef]
- Gao, P.; Zhang, Y.; Chen, X.; Wu, Z.; Zhang, Q.; Zhang, S. OPGs: Promising anode materials with high specific capacity and rate capability for Li/Na ion batteries. Nanoscale 2018, 10, 17942–17948. [Google Scholar] [CrossRef]
- Chen, J.H.; Autès, G.; Alem, N.; Gargiulo, F.; Gautam, A.; Linck, M.; Kisielowski, C.; Yazyev, O.V.; Louie, S.G.; Zettl, A. Controlled growth of a line defect in graphene and implications for gate-tunable valley filtering. Phys. Rev. B 2014, 89, 121407. [Google Scholar] [CrossRef] [Green Version]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications, 2nd ed.; Computational Science Series; Academic Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Large-Scale Atomic/Molecular Massively Parallel Simulator (LAMMPS). Available online: http://lammps.sandia.gov (accessed on 28 February 2020).
- Silvera, I.F. The solid molecular hydrogens in the condensed phase: Fundamentals and static properties. Rev. Mod. Phys. 1980, 52, 393–452. [Google Scholar] [CrossRef]
- Buch, V. Path integral simulations of mixed para-D2 and ortho-D2 clusters: The orientational effects. J. Chem. Phys. 1994, 100, 7610–7629. [Google Scholar] [CrossRef]
- Michels, A.; de Graaff, W.; Seldam, C.T. Virial coefficients of hydrogen and deuterium at temperatures between −175 °C and +150 °C. Conclusions from the second virial coefficient with regards to the intermolecular potential. Physica 1960, 26, 393–408. [Google Scholar] [CrossRef]
- Darkrim, F.; Levesque, D. Monte Carlo simulations of hydrogen adsorption in single-walled carbon nanotubes. J. Chem. Phys. 1998, 109, 4981–4984. [Google Scholar] [CrossRef]
- Ustinov, E.; Tanaka, H.; Miyahara, M. Low-temperature hydrogen-graphite system revisited: Experimental study and Monte Carlo simulation. J. Chem. Phys. 2019, 151, 024704. [Google Scholar] [CrossRef]
- Gehringer, D.; Dengg, T.; Popov, M.N.; Holec, D. Interactions between a H2 Molecule and Carbon Nanostructures: A DFT Study. C J. Carbon Res. 2020, 6, 16. [Google Scholar] [CrossRef] [Green Version]
- Aga, R.S.; Fu, C.L.; Krčmar, M.; Morris, J.R. Theoretical investigation of the effect of graphite interlayer spacing on hydrogen absorption. Phys. Rev. B 2007, 76, 165404. [Google Scholar] [CrossRef]
- Baburin, I.A.; Klechikov, A.; Mercier, G.; Talyzin, A.; Seifert, G. Hydrogen adsorption by perforated graphene. Int. J. Hydrog. Energy 2015, 40, 6594–6599. [Google Scholar] [CrossRef] [Green Version]
- Jain, V.; Kandasubramanian, B. Functionalized graphene materials for hydrogen storage. J. Mater. Sci. 2020, 55, 1865–1903. [Google Scholar] [CrossRef]
- Lamari, F.D.; Levesque, D. Hydrogen adsorption on functionalized graphene. Carbon 2011, 49, 5196–5200. [Google Scholar] [CrossRef]
- Dicko, M.; Seydou, M.; Lamari, F.D.; Langlois, P.; Maurel, F.; Levesque, D. Hydrogen adsorption on graphane: An estimate using ab-initio interaction. Int. J. Hydrog. Energy 2017, 42, 10057–10063. [Google Scholar] [CrossRef]
- Firlej, L.; Kuchta, B.; Lazarewicz, A.; Pfeifer, P. Increased H2 gravimetric storage capacity in truncated carbon slit pores modeled by Grand Canonical Monte Carlo. Carbon 2013, 53, 208–215. [Google Scholar] [CrossRef]
- Builes, S.; Sandler, S.I.; Xiong, R. Isosteric Heats of Gas and Liquid Adsorption. Langmuir 2013, 29, 10416–10422. [Google Scholar] [CrossRef] [PubMed]







| Source | Alias | Potential | Interaction | (meV) | (Å) | Notes |
|---|---|---|---|---|---|---|
| Darkrim-Levesque [26] | DL | LJ (12-6) | H–H | 3.163 | 2.958 | Originally from [25] |
| LJ (12-6) | C–C | 2.430 | 3.400 | |||
| LJ (12-6) | C–H | 2.772 | 3.179 | Lorentz-Berthelot | ||
| Ustinov et al. [27] | UTM | Mie (10-6) | H–H | 2.284 | 3.129 | Implicit FH at 77.35 K |
| Mie (10-6) | C–H | 4.317 | 2.800 | Implicit FH at 77.35 K | ||
| This work (graphene) | G-LJ | LJ (12-6) | C–H | 4.951 | 3.037 | Fit to vdW-DFT data |
| This work (POP-graphene) | P-LJ | LJ (12-6) | C–H | 5.055 | 3.031 | Fit to vdW-DFT data |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popov, M.N.; Dengg, T.; Gehringer, D.; Holec, D. Adsorption of H2 on Penta-Octa-Penta Graphene: Grand Canonical Monte Carlo Study. C 2020, 6, 20. https://doi.org/10.3390/c6020020
Popov MN, Dengg T, Gehringer D, Holec D. Adsorption of H2 on Penta-Octa-Penta Graphene: Grand Canonical Monte Carlo Study. C. 2020; 6(2):20. https://doi.org/10.3390/c6020020
Chicago/Turabian StylePopov, Maxim N., Thomas Dengg, Dominik Gehringer, and David Holec. 2020. "Adsorption of H2 on Penta-Octa-Penta Graphene: Grand Canonical Monte Carlo Study" C 6, no. 2: 20. https://doi.org/10.3390/c6020020
APA StylePopov, M. N., Dengg, T., Gehringer, D., & Holec, D. (2020). Adsorption of H2 on Penta-Octa-Penta Graphene: Grand Canonical Monte Carlo Study. C, 6(2), 20. https://doi.org/10.3390/c6020020