The Effect of Hydrogen on the Electrical Properties of the Graphene Nanomeshes

Abstract

This paper is devoted to the in silico study of the electronic properties and electrical conductivity of hydrogenated graphene nanomesh (GNM). It is found that the conductivity of GNM can be controlled by varying the type of hydrogenation. Due to the hydrogenation of the nanohole edges by one or two hydrogen atoms, the energy gap can be changed, the anisotropy of the electrical conductivity can be enhanced, and the electron work function can be controlled. By varying the type of hydrogenation, it is possible to form conductive and insulating paths on 2D GNM. Thus, a certain combination of the sp²- and sp³-topologies of the GNM edge atoms allows one to fully “turn off” the electronic conductivity in all directions or, conversely, “turn on” the desired direction for current transfer.

1. Introduction

In this paper, we study the possibility of controlling the graphene nanomesh (GNM) electrical properties by hydrogenation of the nanohole edge atoms. As is known, GNM is now actively being studied. The GNM samples with different architecture of nanoholes have already been synthesized [1]. Currently, many methods have been developed for the fabrication of GNM: nanoprint lithography, nanosphere lithography, block copolymer lithography, and local catalytic hydrogenation by nanoparticles [2]. The stability of nanoholes is ensured by both the hydrogenation of edge atoms and their modification by silicon atoms [3,4]. The possibility of hydrogen accumulation in GNM using transition metal atoms such as Sc trapped in nanoholes is also investigated. It has been shown that one Sc atom can adsorb four H₂ molecules with a binding energy of 0.13 eV per one H₂ molecule [5]. The search for ways to control the properties of GNM by varying the shape and size of nanoholes, as well as their periodicity is being actively carried out [6,7,8,9,10,11]. For example, the effect of nanohole size and nanohole shape (round, square, and equilateral triangles) on the electronic properties of graphene nanoribbons is investigated [6]. It has been found that the structure of the GNM energy zone is sensitive to the shape and size of nanoholes, and also depends on the type of the super-cell edge (armchair or zigzag). Lopata et al. showed that it is possible to achieve a balance between the density of edge localized states and the doping of the nanohole edge atoms with oxygen atoms [9]. It has been established that the achieved balance can serve as a key factor in controlling the semiconductor properties of GNM. Another interesting fact is the discovery of structural regularities in the appearance and disappearance of the energy gap. It has been found that the maximum gap corresponds to a benzoid pattern, which is a certain type of hexagon ring and a certain ratio between the number of hexagons in the super-cell and the number of edge hexagons forming a nanohole [10]. It has been established that the energy gap is also very sensitive to the neck width (the minimum distance between the edge atoms of neighboring nanoholes). The gap decreases with increasing neck width. This dependence is used in the operation of field-effect transistors. Thus, the GNM with nanoholes in the form of rectangles (r-GNM) and circles (c-GNM) with different neck widths was studied by Yuan et al. [11]. It has been shown that GNM-based field-effect transistors with different neck widths have different I_on/I_off ratios. In particular, it has been found that r-GNM-based devices with a neck width of 30 nm have the highest ratio I_on/I_off ~100, and the r-GNM energy gap is 0.23 eV. Also, the hydrogenation of edge atoms affects the size of the gap. This inevitably affects the transport properties and current-voltage characteristics. At the same time, this phenomenon is being studied for 1D-GNM [12]. Also, the effect of the different hydrogen terminations on electrical conductivity has not been studied at all. It has been experimentally proved that a GNM nanoribbon with a width of 10–1000 μm with a periodicity of 10–39 nm and neck width of 5–7 nm has a conductivity of 50–100 times that of graphene nanoribbons of a similar width [13].

This work is devoted to the search for a mechanism for controlling the conductivity and electronic properties of GNM using various types of hydrogenation of the nanohole edge atoms by in silico methods. Various types of hydrogenation are understood as sp²- and sp³-topological types of hydrogenation of the nanohole edge atoms.

2. Computational Details and Models

We consider a GNM model with nanoholes of almost circular symmetrical shape with a diameter of 1.2 nm. Single-layer GNMs with a neck width of 5 ± 2 nm [13] and also with a neck width of 0.75 nm at a nanohole diameter of 0.3 nm have been experimentally obtained [14]. We have chosen the average diameter of the nanohole. The distance between the nanoholes called the “neck width” is defined as the smallest edge-to-edge distance between two neighbor nanoholes. Figure 1a shows a fragment of the investigated GNM. The super-cell is indicated by a blue box. The neck width in the X and Y directions is also indicated. These values are designated as nw_x and nw_y. The values of nw_x = 0.75 nm and nw_y = 1.08 nm fully correspond to the experimentally obtained values. The dimensions of the super-cell are 2.46 × 2.55 nm.

Next, the hydrogenation of the nanohole edge atoms of obtained super-cell was carried out. As noted above, various types of hydrogenation were considered. In the case of the attachment of one hydrogen atom to the edge carbon atom, the so-called mono-hydrogenation was observed, that is, the sp²-topology of the nanohole edge. In the case of the attachment of two hydrogen atoms at once, di-hydrogenation was observed, i.e., the sp³-topology of the nanohole edge. Hybrid types of hydrogenation are also possible when some nanohole edge atoms have an sp²-topology, while others have an sp³-topology. The obtained atomistic models of super-cells are shown in Figure 1b. Hydrogen atoms are marked in green. We examined five types of hydrogenation: (1) all edge atoms with sp²-topology (it is designated as 1/1/1 in Figure 1b); (2) one edge atom has two hydrogen atoms, and the next two atoms, one at a time (it is designated as 2/1/1 in Figure 1b); (3) a clear alternation of sp²- and sp³-topologies through one edge atom (it is designated as 2/1/2 in Figure 1b); (4) two edge atoms have sp²-topology, and the next one has sp³-topology (it is designated as 2/2/1 in Figure 1b); (5) all edge atoms have sp³-topology (it is designated as 2/2/2 in Figure 1b).

The simulation was carried out using the DFTB+ [15,16] and Kvazar–Mizar [17,18] software packages, which implements the self-consistent charge density functional tight-binding (SCC-DFTB) quantum method [19]. Using this method, the atomic structure of all super-cells was determined, and the energy parameters were calculated. A great advantage of the SCC-DFTB method is the ability to study materials in which super-cells contain a thousand or more atoms. In this work, the initial GNM super-cell (before hydrogenation) includes 186 atoms (Figure 1a). In this regard, we use the SCC-DFTB method. Using this method and the above software packages, we first predicted the atomic structure and electronic properties of new carbon nanomaterials [20,21]. The equilibrium super-cell configurations were found as a result of a double optimization, i.e., the translation vectors of the super-cell were optimized, and for each set of translation vectors, the atomic network was optimized by minimizing the super-cell total energy over all the coordinates of all atoms.

The calculations of the electron transmission function T(E) and electrical conductivity G were carried out using the Keldysh nonequilibrium Green function technique, which is based on many-body perturbation theory and diagram techniques [22], as well as using the Landauer–Buttiker formalism, which allows studying the electron transport with regard to elastic scattering of electrons on defects [23]. The electron transmission function T(E) is determined by the expression:

$$T\left(E\right)=\frac{1}{N}{\displaystyle \sum _{k=1}^{N}Tr\left({\Gamma }_s\left(E\right)G_C^A\left(E\right){\Gamma }_D\left(E\right)G_C^R\left(E\right)\right)}$$

(1)

where $G_C^A$, $G_C^R$ are the advanced and retarded Green matrices describing contact with electrodes ${\Gamma }_s\left(E\right)$, ${\Gamma }_D\left(E\right)$ are the broadening matrices for the source and drain, k is the wave number, N is the number of k-points in the reciprocal space. Static conductivity is described by the expression

$$G=\frac{I}{V}=\frac{2e^2}{h}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}T\left(E\right)}{F}_T\left(E-E_F\right)dE$$

(2)

where E_F is the Fermi energy of the material of the contacts which are connected to the object under study, e is the electron charge, h is the Planck constant, e²/h is the conductance quantum, F_T is the thermal broadening function, I is the current through the device (conductive channel), V is the bias voltage. The factor «2» takes into account the spin of the electrons.

To calculate the electrical conductivity of atomistic models of GNMs with polyatomic super-cells, we used the original method for accelerating the calculations of the electron transmission function T(E). The main idea of this method is as follows. Since, in the case of periodic structures, the transmission function T(E) has a step shape for each fixed wave number k, this makes it possible to extrapolate T(E) with good accuracy at intermediate points by determining jumps in the transmission function profile. Thus, this method allows one to calculate the transmission function T(E) for a small number of k-points of the first Brillouin zone, and then interpolate it for any k-point of the first Brillouin zone and obtain the complete transmission function T(E). This method is described in detail in our previous work by the example of some models of pillared graphene [24]. It allows us to calculate the T(E) and G functions for super-cells with 100–2000 atoms. The calculations of T(E) and G functions using this method were carried out in Kvazar–Mizar software package.

3. Results and Discussion

According to the results of the calculation of the electronic structure and energy parameters, the energy gap (E_gap) and the Fermi level (E_F) were determined for all types of hydrogenation under study. The profiles of the density of states (DOS) were also calculated.

Table 1. Energy characteristics of GNM with various types of hydrogenation of the nanohole edges.

Structure Type	EF, eV	Egap, eV
GNM	−4.73	0.06
GNM−1/1/1 H	−4.64	0.09
GNM−2/1/1 H	−4.49	0.23
GNM−2/1/2 H	−4.43	0.00
GNM−2/2/1 H	−4.35	0.16
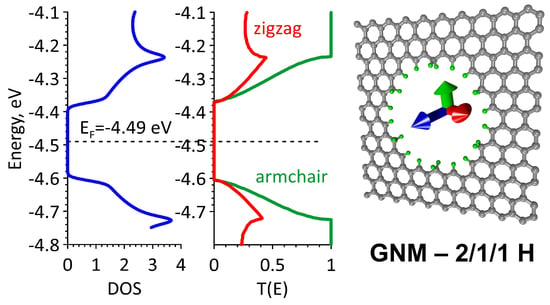
GNM−2/2/2 H	−4.26	0.00

shows the energy characteristics of GNM with various types of hydrogenation of the nanohole edges. DOS graphs are shown in Figure 2 in blue. The dashed line marks the Fermi level. An analysis of the obtained data revealed an interesting effect. A small gap (E_gap ~ 0.1 eV) of initial non-hydrogenated GNM fully disappears in the case of full hydrogenation, that is, when each edge atom of the nanohole has an sp³-topology (full saturation of the bonds), as well as in the case of 2/1/2. The energy gap becomes equal to zero and the Fermi level shifts up (in the direction of zero electron-volt). In the case of complete hydrogenation, the Fermi level shifts by the maximum value, i.e., by almost 0.5 eV. That is, we can say that the GNM–2/2/2 H structure is a conductor with a lower electron work function as compared to the original GNM, pure graphene, and carbon nanotubes, in which the Fermi level is in the range of −4.75–−4.50 eV. It should be noted here that the work function is estimated as the difference between zero electron-volts and Fermi energy E_F. In other cases of hydrogenation, the gap increases. A large energy gap was found in GNM–2/1/1 H. The analysis of DOS graphs shows that the energy profile is asymmetric with respect to the Fermi level only for the hybrid types of GNM hydrogenation (see Figure 2b,d). Other types of hydrogenation are characterized by (1) the presence of an energy gap, and (2) a low DOS in the valence and conduction bands in the range of E_F ± 0.2 eV. In this range, for example, the DOS of non-hydrogenated GNM is almost two times higher. The DOS profiles of the GNM–1/1/1 H and GNM–2/2/2 H structures differ significantly from all others by the presence of distinct peaks near the Fermi level. These DOS peaks are 25–30 arb. units, which is several times higher than the corresponding value for non-hydrogenated GNM.

The electron transmission function T(E) (Equation (1)) is an important indicator of electrical conductivity G (Equation (2)) because it characterizes the probability of the passage of electrons through this structure. Like the DOS function, the function T(E) can be characterized by a gap, i.e., a zero region of electron transmission in the energy range near the Fermi level. In addition, the function T(E) can vary dramatically depending on the direction of current transfer, that is, it exhibits anisotropy of electrical conductivity. The profile of this function near the Fermi level directly determines the electrical conductivity G [24]. The calculated T(E) graphs are shown in Figure 2. The green color indicates the T(E) graphs in the armchair direction (along the Y-axis—see Figure 1), the red color indicates the T(E) graphs along the zigzag direction (along the X-axis). The units of the function T(E) are the conductance quanta e²/h. The symmetry features of the T(E) profiles repeat the features of the DOS profiles. However, the difference between the two directions of the current transfer is very noticeable. And here you can see that the direction of the armchair (green graphs) stands out, that is, in this direction, the electrical conductivity is much higher compared to the zigzag direction. Figure 2 clearly demonstrates that the electrical conductivity in the armchair direction (green graphs) is much higher as compared to the zigzag direction. The function T(E) always reaches unity (one conduction channel) in the armchair direction, and in the zigzag direction, its values do not exceed 0.5. This indicates a strong anisotropy of electrical conductivity in all GNM variations, regardless of the presence of hydrogen atoms and the topology of their distribution on the nanohole edge atoms. The case of hydrogenation with fully saturated bonds (GNM–2/2/2 H) stands out especially. Zero conductivity is observed for this GNM structure over a large energy range for the zigzag direction. That is, even without calculating the electrical conductivity, we can conclude that the GNM nanomaterial does not conduct current at all in this direction. The reason for this difference in the behavior of the function T(E) depending on the type of hydrogenation of the nanohole edges is the redistribution of the electron density, which inevitably occurs in this case.

The calculated values of the electrical conductivity G and resistance R are shown in

Table 2. Electroconductive characteristics of GNM with various types of hydrogenation of the nanohole edges.

Structure Type	Zigzag Direction		Armchair Direction
	G, µS	R, kOhm	G, µS	R, kOhm
GNM	4.96	201.6	17.9	55.8
GNM–1/1/1 H	2.79	358.4	5.89	169.7
GNM–2/1/1 H	0.227	4405.2	0.35	2857.1
GNM–2/1/2 H	15.9	62.8	11.9	84.0
GNM–2/2/1 H	1.29	775.1	2.97	336.7
GNM–2/2/2 H	0.0005	2,000,000.0	41.2	24.2

. The calculations were carried out at 300 K. According to the analysis of the T(E) profile, the GNM–2/2/2 H nanomaterial has the highest conductivity, but only in the armchair direction. In the other direction, the GNM–2/2/2 H nanomaterial is an insulator. Such a strong anisotropy is caused by two facts: (1) full saturation of the bonds of the edge carbon atoms and (2) the initial anisotropy of the GNM electrical conductivity. Figure 2 shows that non-hydrogenated GNM exhibits better conductive properties in the armchair direction. Thus, saturating all the bonds of the edge atoms, it is possible to “switch” the current transfer, obtaining conducting paths in one direction and insulating paths in the other direction. A similar effect is observed for the case of GNM–1/1/1 H, but on the contrary, the current transfer is completely absent in the armchair direction. However, the conductivity in the zigzag direction is low. Other types of hydrogenation can fully turn off conductivity. For example, in the case of GNM–2/1/1 H, the conductivity fully disappears, and the resistance increases to 2–4 kΩ in both directions.

4. Conclusions

As a result of in silico studies using the quantum SCC-DFTB method, new knowledge has been obtained on the effect of the type of hydrogenation of the GNM nanohole edge atoms on the electronic properties and electrical conductivity anisotropy of the GNM. Using the example of GNM with round nanoholes with a diameter of 1.2 nm, it was shown that the complete saturation of the bonds of the nanohole edge atoms allows one to “turn on” the current transfer in one direction and completely “turn off” in the opposite direction. The maximum shift of the Fermi level to the right is characteristic for this type of hydrogenation, which leads to a lower value of the electron work function as compared to graphene and nanotubes. This makes such a nanomaterial very promising as a source of autoelectrons for micro- and nanoelectronics devices. A certain combination of the sp²- and sp³-topologies of the GNM edge atoms allows one to “turn off” completely the electronic conductivity in all directions or, conversely, “turn on” the desired direction for current transfer.

The conducted studies open up new questions and new perspectives. A very interesting question remains about the nature of the appearance of anisotropy in various hydrogenation methods. To answer this question, many in silico studies must be carried out, including studies of LDOS on the GNM atoms in all cases of hydrogenation.