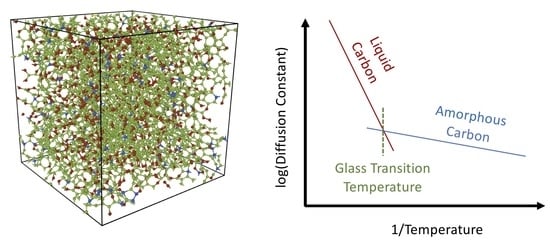
Evidence for Glass Behavior in Amorphous Carbon
Abstract
:1. Introduction
2. Methodology
3. Results and Discussion
3.1. Tersoff Potential at 1.5 g/cc
3.2. Comparison between Potentials and Densities
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References and Note
- Vetter, J. 60 years of DLC coatings: Historical highlights and technical review of cathodic arc processes to synthesize various DLC types, and their evolution for industrial applications. Surf. Coat. Technol. 2014, 257, 213–240. [Google Scholar] [CrossRef]
- Schwan, J.; Ulrich, S.; Roth, H.; Ehrhardt, H.; Silva, S.R.P.; Robertson, J.; Samlenski, R.; Brenn, R. Tetrahedral amorphous carbon films prepared by magnetron sputtering and dc ion plating. J. Appl. Phys. 1996, 79, 1416–1422. [Google Scholar] [CrossRef] [Green Version]
- Schwan, J.; Ulrich, S.; Theel, T.; Roth, H.; Ehrhardt, H.; Becker, P.; Silva, S. Stress-induced formation of high-density amorphous carbon thin films. J. Appl. Phys. 1997, 82, 6024–6030. [Google Scholar] [CrossRef] [Green Version]
- Morgan, M. Electrical conduction in amorphous carbon films. Thin Solid Films 1971, 7, 313–323. [Google Scholar] [CrossRef]
- Aksenov, I.; Vakula, S.; Padalka, V.; Strelnitskii, V.; Khoroshikh, V. High-efficiency source of pure carbon plasma. Sov. Phys. Tech. Phys. 1980, 25, 1164–1166. [Google Scholar]
- McKenzie, D.; Muller, D.; Pailthorpe, B. Compressive-stress-induced formation of thin-film tetrahedral amorphous carbon. Phys. Rev. lett. 1991, 67, 773. [Google Scholar] [CrossRef] [PubMed]
- Fallon, P.; Veerasamy, V.; Davis, C.; Robertson, J.; Amaratunga, G.; Milne, W.; Koskinen, J. Properties of filtered-ion-beam-deposited diamondlike carbon as a function of ion energy. Phys. Rev. B 1993, 48, 4777. [Google Scholar] [CrossRef]
- Aisenberg, S.; Chabot, R. Ion-beam deposition of thin films of diamondlike carbon. J. Appl. Phys. 1971, 42, 2953–2958. [Google Scholar] [CrossRef]
- Lifshitz, Y.; Kasi, S.; Rabalais, J. Carbon (sp3) Film Growth from Mass Selected Ion Beams: Parametric Investigations and Subplantation Model; Materials Science Forum: Baech, Switzerland, 1990; Volume 52, pp. 237–290. [Google Scholar]
- McKenzie, D.; Yin, Y.; Marks, N.; Davis, C.; Kravtchinskaia, E.; Pailthorpe, B.; Amaratunga, G. Tetrahedral amorphous carbon properties and applications. J. Non Cryst. Solids 1993, 164–166, 1101–1106. [Google Scholar] [CrossRef]
- Anders, S.; Diaz, J.; Ager, J.W.; Yu Lo, R.; Bogy, D.B. Thermal stability of amorphous hard carbon films produced by cathodic arc deposition. Appl. Phys. Lett. 1997, 71, 3367–3369. [Google Scholar] [CrossRef] [Green Version]
- Ferrari, A.C.; Kleinsorge, B.; Morrison, N.A.; Hart, A.; Stolojan, V.; Robertson, J. Stress reduction and bond stability during thermal annealing of tetrahedral amorphous carbon. J. Appl. Phys. 1999, 85, 7191–7197. [Google Scholar] [CrossRef]
- Savvatimskiy, A. Carbon at High Temperatures; Springer: Berlin, Germany, 2015; Volume 134. [Google Scholar]
- Marks, N.A. Evidence for subpicosecond thermal spikes in the formation of tetrahedral amorphous carbon. Phys. Rev. B 1997, 56, 2441–2446. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Chem. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- LAMMPS. Available online: http://lammps.sandia.gov (accessed on 25 July 2020).
- de Tomas, C.; Suarez-Martinez, I.; Marks, N.A. Graphitization of amorphous carbons: A comparative study of interatomic potentials. Carbon 2016, 109, 681–693. [Google Scholar] [CrossRef]
- de Tomas, C.; Aghajamali, A.; Jones, J.L.; Lim, D.J.; López, M.J.; Suarez-Martinez, I.; Marks, N.A. Transferability in interatomic potentials for carbon. Carbon 2019, 155, 624–634. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef] [Green Version]
- Tersoff, J. Empirical interatomic potential for carbon, with applications to amorphous carbon. Phys. Rev. Lett. 1988, 61, 2879–2882. [Google Scholar] [CrossRef] [Green Version]
- Brenner, D.W.; Shenderova, O.A.; Harrison, J.A.; Stuart, S.J.; Ni, B.; Sinnott, S.B. A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons. J. Phys. Condens. Matter 2002, 14, 783–802. [Google Scholar] [CrossRef]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef] [Green Version]
- Srinivasan, S.G.; van Duin, A.C.T.; Ganesh, P. Development of a ReaxFF potential for carbon condensed phases and its application to the thermal fragmentation of a large fullerene. J. Phys. Chem. A 2015, 119, 571–580. [Google Scholar] [CrossRef]
- Marks, N.A. Generalizing the environment-dependent interaction potential for carbon. Phys. Rev. B 2000, 63. [Google Scholar] [CrossRef]
- Schultz, P.A.; Leung, K.; Stechel, E.B. Small rings and amorphous tetrahedral carbon. Phys. Rev. B 1999, 59, 733–741. [Google Scholar] [CrossRef]
- Seidl, M.; Loertig, T.; Zifferer, G. Molecular dynamics simulations on the glass-to-liquid transition in high density amorphous ice. Z. Phys. Chem. 2009, 223, 1047–1062. [Google Scholar] [CrossRef]
- Weng, L.; Elliott, G.D. Dynamic and thermodynamic characteristics associated with the glass transition of amorphous trehalose–water mixtures. Phys. Chem. Chem. Phys. 2014, 16, 11555–11565. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Geyer, U.; Johnson, W.L.; Schneider, S.; Qiu, Y.; Tombrello, T.A.; Macht, M. Small atom diffusion and breakdown of the Stokes–Einstein relation in the supercooled liquid state of the Zr46.7Ti8.3Cu7.5Ni10Be27.5 alloy. Appl. Phys. Lett. 1996, 69, 2492–2494. [Google Scholar] [CrossRef] [Green Version]
- Alkorta, I.; Elguero, J. The carbon–carbon bond dissociation energy as a function of the chain length. Chem. Phys. Lett. 2006, 425, 221–224. [Google Scholar] [CrossRef]
- Dissociation energies for carbon and silicon s-bonds in the diamond lattice are calculated by dividing the cohesive energy (Ecoh) by two. For carbon, Ecoh = 7.35 eV/atom (Shin et al., J. Chem. Phys. 2014, 140, 114702), while for silicon, Ecoh = 4.63 eV/atom (Yin & Cohen, Phys. Rev. B 1981, 24, 6121–6124).
- Kirschbaum, J.; Teuber, T.; Donner, A.; Radek, M.; Bougeard, D.; Böttger, R.; Hansen, J.L.; Larsen, A.N.; Posselt, M.; Bracht, H. Self-Diffusion in Amorphous Silicon by Local Bond Rearrangements. Phys. Rev. Lett. 2018, 120, 225902. [Google Scholar] [CrossRef]
- Napolitano, S.; Glynos, E.; Tito, N.B. Glass transition of polymers in bulk, confined geometries, and near interfaces. Rep. Prog. Phys. 2017, 80, 036602. [Google Scholar] [CrossRef]
- Zhao, G.; Mu, H.F.; Wang, D.H.; Yang, C.L.; Wang, J.K.; Song, J.Y.; Shao, Z.C. Structural and dynamical change of liquid carbon with pressure: ab initio molecular dynamics simulations. Phys. Scr. 2013, 88, 045601. [Google Scholar] [CrossRef]
- Marks, N. Modelling diamond-like carbon with the environment-dependent interaction potential. J. Phys. Condens. Matter 2002, 14, 2901–2927. [Google Scholar] [CrossRef]
- Ruoff, R.S. A perspective on objectives for carbon science. Carbon 2018, 132, 802. [Google Scholar] [CrossRef]







| Potential | Density (g/cc) | (K) | (eV) | (eV) |
|---|---|---|---|---|
| Tersoff | 1.5 | 3770 ± 370 | 4.49 ± 0.30 | 0.37 ± 0.06 |
| 2.0 | 3660 ± 230 | 4.35 ± 0.18 | 0.34 ± 0.05 | |
| 2.5 | 3530 ± 220 | 4.06 ± 0.15 | 0.30 ± 0.06 | |
| 3.0 | 3580 ± 210 | 3.98 ± 0.13 | 0.33 ± 0.05 | |
| REBO-II | 1.5 | 2930 ± 370 | 3.20 ± 0.24 | 0.34 ± 0.10 |
| 2.0 | 2830 ± 240 | 3.03 ± 0.11 | 0.31 ± 0.09 | |
| 2.5 | 2710 ± 260 | 2.89 ± 0.14 | 0.31 ± 0.09 | |
| 3.0 | 2800 ± 310 | 2.97 ± 0.20 | 0.32 ± 0.08 | |
| AIREBO | 1.5 | 3210 ± 350 | 3.66 ± 0.09 | 0.27 ± 0.14 |
| 2.0 | 3360 ± 130 | 3.80 ± 0.06 | 0.26 ± 0.05 | |
| 2.5 | 3420 ± 160 | 3.59 ± 0.06 | 0.29 ± 0.05 | |
| 3.0 | 3570 ± 220 | 3.59 ± 0.15 | 0.29 ± 0.03 | |
| ReaxFF | 1.5 | 2720 ± 470 | 2.86 ± 0.32 | 0.32 ± 0.11 |
| 2.0 | 2620 ± 400 | 2.87 ± 0.30 | 0.24 ± 0.10 | |
| 2.5 | 2680 ± 380 | 2.85 ± 0.26 | 0.25 ± 0.10 | |
| 3.0 | 2620 ± 300 | 2.64 ± 0.17 | 0.21 ± 0.10 | |
| EDIP | 1.5 | 3190 ± 840 | 4.39 ± 0.86 | 0.26 ± 0.03 |
| 2.0 | 3050 ± 740 | 4.13 ± 0.75 | 0.31 ± 0.04 | |
| 2.5 | 2660 ± 570 | 3.43 ± 0.57 | 0.22 ± 0.06 | |
| 3.0 | 2630 ± 290 | 3.12 ± 0.22 | 0.22 ± 0.09 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Best, S.; Wasley, J.B.; de Tomas, C.; Aghajamali, A.; Suarez-Martinez, I.; Marks, N.A. Evidence for Glass Behavior in Amorphous Carbon. C 2020, 6, 50. https://doi.org/10.3390/c6030050
Best S, Wasley JB, de Tomas C, Aghajamali A, Suarez-Martinez I, Marks NA. Evidence for Glass Behavior in Amorphous Carbon. C. 2020; 6(3):50. https://doi.org/10.3390/c6030050
Chicago/Turabian StyleBest, Steven, Jake B. Wasley, Carla de Tomas, Alireza Aghajamali, Irene Suarez-Martinez, and Nigel A. Marks. 2020. "Evidence for Glass Behavior in Amorphous Carbon" C 6, no. 3: 50. https://doi.org/10.3390/c6030050
APA StyleBest, S., Wasley, J. B., de Tomas, C., Aghajamali, A., Suarez-Martinez, I., & Marks, N. A. (2020). Evidence for Glass Behavior in Amorphous Carbon. C, 6(3), 50. https://doi.org/10.3390/c6030050