Conformational Analysis of [60]PCBM from DFT Simulations of Electronic Energies, Bond Strain and the ¹³C NMR Spectrum: Input Geometry Determination and Ester Bond Rotation Dynamics

Abstract

With the aim of determining the best input geometry for DFT calculations of [60]PCBM, the geometry of 24 chemically possible [60]PCBM conformers were optimised and their electronic energies and average bond strains were determined. A DFT analysis of the relevant dihedral angles provided insights into the dynamical behaviour of the ester group through sterically restricted bond rotations. In addition, the ¹³C NMR spectra of the six better performing conformers were simulated and compared with an experiment. There is a close correlation between average bond strain, total electronic energy and mean absolute error of the simulated ¹³C NMR spectra of the ester carbons. The best overall candidate conformer for the input geometry had the C61-C4, C4-C3 and C3-C2 single bonds of the alkyl chain in syn, anti and anti arrangements, respectively, and had the C2-C1 and C1-O single bonds of the ester in syn and anti arrangements, respectively. This contrasts strikingly with most representations of PCBM in the literature, which depict all relevant bonds in anti arrangements.

1. Introduction

[60]PCBM, or, correctly, methyl 4-[3′H-phenyl cyclopropa(C₆₀-I_h) [5,6] fulleren-1,9-yl]butanoate, was first synthesised in 1995 as one of six novel homo- and methano-bridged cyclo-additions to C₆₀ [1]. Since then, [60]PCBM has become one of the most important n-type molecules in organic electronics. The initial application was as the archetypal electron acceptor in bulk heterojunction photovoltaics [2]. However, it has gone on to be used in many other nano-electronic applications, including perovskite photovoltaics [3], field effect transistors [4,5,6], light emitting diodes [7,8] and photodetectors [9,10,11].

To aid in the understanding of these applications experimental research has been supported by hundreds of quantum chemical ab initio calculations and simulations. Indeed, a Google search carried out on the day of submission for “PCBM” AND “DFT” (where AND is logical) returned over 10⁵ internet matches, and a Web of Science search indicated that about 10% of primary sources on [60]PCBM involve quantum chemical calculations. However, to perform accurate calculations/simulations, an accurate input geometry needs to be used. Solution ¹³C NMR spectroscopy indicates that [60]PCBM has C_S molecular point group symmetry in which the phenyl group bisects the mirror plane [1]. In addition, ¹H NMR spectroscopy shows well-defined second-order spin–spin coupling effects indicative of substantially hindered rotation about the single bonds between heavy atoms of the ester group [12]. With this, [60]PCBM has potential to exist as 32 conformers that are consistent with [60]PCBM’s C_S symmetry, of which 24 are chemically possible.

We trialled all 24 conformers, aiming to determining the best input geometry for simulations of non-solid [60]PCBM. Although the results were obtained in relation to simulating the ¹³C NMR spectrum, they are generally applicable. In addition, although they were obtained in relation to a liquid phase experiment, they may provide insights into the mechanism of packing of [60]PCBM in the solid phase. This is because solid samples used in solar cells and other organic electronics applications are almost invariably obtained from solution (e.g., via spin coating), where the molecule would initially have the conformational structure, and need to conform during condensation to the restraints on the dynamical behaviour of the ester group, obtained here.

2. Materials and Methods

All ab initio calculations were performed using the Gaussian 16 package [13]. The gauge independent atomic orbitals (GIAO) DFT simulations of the ¹³C NMR spectrum employed the ωB97XD method coupled with the cc-pVTZ basis set. The range separation parameter for electron exchange, ω, was set to zero bohr⁻¹, while the other parameters were kept at their default values, and the SCRF solvation model was used. This is a method we previously found [14] to substantially outperform the very commonly used B3LYP method when specifically applied to PCBM. All other calculations were carried out at a B3LYP/cc-pVTZ level together with Grimme-D3 empirical dispersion with Becke–Johnson damping.

An initial input geometry for PCBM generated using Gaussview software [15] and subsequently freely optimised to a minimum with tight cut-offs. A frequency calculation test of this optimised geometry revealed no vibrational frequencies, indicating that the optimisation converged to a minimum. The optimised geometry did not, however, conform to any of the 24 C_S-symmetry conformers. Instead, it had C₁ symmetry with the ester lying slightly off the mirror plane. To ensure than the conformers had the experimental C_S symmetry, starting with the optimised geometry, the five relevant dihedral angles of each conformer were set and constrained to either 0° or 180°. Each of the conformers was then re-optimised subject to the 5 constrained dihedral angles (all other bond dihedral angles, bond angles and bond lengths were freely varied).

The [60]PCBM used in this study was synthesised following an adaption of the original method of Hummelen et al., [1] purified by HPLC on a silica semi-preparative column and characterised at room temperature by ¹³C NMR spectroscopy at 600 MHz (125 MHz for C) in carbon disulphide solution. A two-page set-by-step description of our synthesis method and an HPLC chromatogram of our purification method was recently published elsewhere [12].

3. Results and Discussion

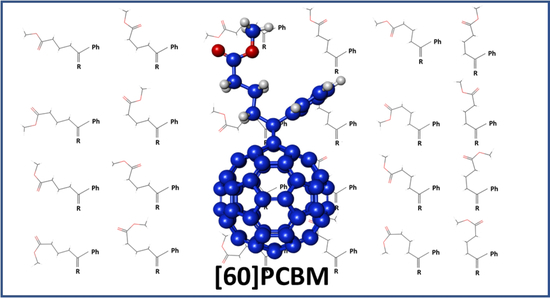
[60]PCBM, as its trivial name suggests, may be considered as consisting of three parts: a phenyl group, a C₆₁ cyclopropafullerenyl group and a butyric acid methyl ester group. The conformational structure of the conjoined phenyl-cyclopropafullerenyl substituent to the ester is trivial. This is because there is only one conformation of that grouping that is consistent with the molecule’s C_s symmetry. This conformer has phenyl carbons C1 and C4 and cyclopropafullerene carbons C20, C30, C31, C40 and C61 on the mirror plane while all other atoms exist as mirrored pairs bisecting the mirror plane.

For the ester group to retain PCBM’s C_S symmetry in solution, all heavy elements of the ester group (C4, C3, C2, C1, both oxygens and the methyl carbon) must lie on the mirror plane. In addition, one of the methyl hydrogens must also be on the mirror plane and the other eight hydrogens of the ester group must exit in mirrored pairs bisecting the mirror plane. To lie on the mirror plane, the dihedral angles of the heavy elements of the ester must be either 0° or 180°. There are no other possible dihedral angles that are consistent with C_S symmetry. These dihedral angles are those of the C61-C4, C4-C3, C3-C2, C2-C1 and C1-O single bonds. With each of the five dihedral angles having one of two values (0° or 180°), there are 2⁵ = 32 C_S-consistent conformers. However, of these 32 possibilities, eight are chemically absurd. This is because for four of them, the ester group would penetrate the fullerene cage, and for the other four conformers, the ester group would penetrate the phenyl ring. This leaves 24 chemically possible conformers.

3.1. Proposed Conformer Nomenclature

To differentiate the 24 remaining conformers while keeping a reasonably short trivial name, we propose the following nomenclature. In parentheses, prefix [60]PCBM with the five relative orientations about the bonds in the ester group, which are designated “s” for syn and “a” for anti with respect to the relevant single bonded heavy elements of the addend that lie on the mirror plane. We present them in the following order: C61-C4, C4-C3, C3–C2, C2–C1 and C1–O, and place a hyphen after the third bond to differentiate the conformational behaviour of the alkyl chain from that of the ester end.

An example is (sas-sa)[60]PCBM, which has C61-C4 syn, C4-C3 anti and C3-C2 syn for the alkyl chain part, and C2-C1 syn and C1-O anti for the COOMe part. A diagram of (sas-sa)[60]PCBM is given in Figure 1, which was randomly chosen to illustrate this naming system. For example, the C61-C4 bond has the attached carbons C3 of the ester and C1 of the phenyl ring in a syn conformation on the mirror plane; hence, the conformation about this bond is denoted as s. On the other hand, the arrangement of the attached carbons to the C3-C4 bond (C2 and C61, respectively) are in an anti a conformation. It must be kept in mind that the s or a designation refers to the heavy elements (C and O).

All 24 possible ester conformations are shown in Figure 2 at their B3LYP/cc-pVTZ optimised geometries. For clarity, as with Figure 1, the conformationally invariant phenyl and cyclopropafullerenyl groups are omitted and only the relevant atoms are shown.

3.2. Bond Strain and Electronic Energy Analysis

In this part of the work, the initial freely optimised geometry (as detailed in Section 2) had its five relevant dihedral set to angles to either 0° (syn) or 180° (anti) to generate the 24 C_S symmetric conformers. The geometries of the 24 conformers were then re-optimised subject to the five dihedral angles, each being constrained as appropriate, while all bond lengths, bond angles and other dihedral angles could freely vary. The initial geometry from which the 24 conformers were generated was at a minimum on the B3LYP/cc-pVTZ potential energy surface. As such, with all 24 conformers being generated from this one optimised structure by varying it along only one coordinate (one dihedral angle), the 24 conformers should be near the minima.

It is apparent from inspecting Figure 2 that many of the bond angles are unrealistic. For example, the C1-C2-C3 bond angle in (aas-ss)[60]PCBM at the end of the second row is exceptionally wide at 138° where about 112° is expected. As further examples of the unrealistic bond angles, the six xxx-ss conformers have their C1-O-Me bond angles ranging from 126.6° to 129.7°. These are all very wide compared to experimentally known values from powder x-ray diffraction studies, −116.0° [16]. Hence, even without simulating the ¹³C NMR spectra of the six xxx-ss conformers, these may be discounted as candidates for the proper input geometry. Similarly, all 12 axx-xx and four ssa-xx conformers have extremely large C61-C4-C3 bond angles, ranging from 120.7°–135.9° (cf. experiment [16] at 114.4°); conversely, the remaining eight sxx-xx conformers (saa-xx and sas-xx) have more realistic angles (ranging from 113.9°–115.4°). This suggests that the 12 axx-xx and four ssa-xx conformers may be also discounted. A full table of every relevant bond angle is given as supporting information (Table S1).

To give a quantitative measure of the bond strain for each of the 24 conformers, all the relevant bond angles for each conformer were measured using Gaussview software [17]. Following this, the absolute differences from the experimental solid state [16] bond angle were obtained, and finally, from these, the mean absolute deviation (MAD) was obtained for each conformer. These 24 MADs are plotted against their relevant conformer in Figure 3. The MADs range from 0.6 to 12.3 degrees per bond angle. Within each of the six xxx- combinations, it is the xxx-ss that have the highest MADs (which were qualitatively rejected earlier in the discussion), validating this method.

The degree of bond strain in the conformers is also likely to be reflected in their total electronic energies. As such, the total electronic energy of each of the 24 conformers is also given in Figure 3. These are presented as relative to the lowest energy conformer, which is set to zero. These energies range up to 153 kJ/mol (1.59 eV) above that of the most stable conformer.

Two initial deductions can be drawn from Figure 3. The first is that there is a very close correlation between MAD of the bond angles and the relative total electronic energy, with remarkably similar trends in both. The second is that entire pattern breaks into two separate series of three separate four-membered groups. One series involves the 12 axx-xx conformers and another involves the 12 sxx-xx conformers, within each series, there are three groups of four conformers (with each group consisting of an xxx-aa, -sa, -as, -ss set).

The members of each of the six groups all follow the same trend. That is, the xxx-aa member is the most stable (having the lowest total electronic energies and bond strain MADs), closely followed by the -sa member. There is then a much larger step to the -as member followed by an even larger step to the -ss member. This indicates that the -COOMe part is quite unstable having the C1-O bond syn and is even more unstable if the C2-C1 bond is also syn. It also indicated that provided the C1-O bond is anti, there is little difference in terms of energy or bond strain on whether the C2-C1 bond is anti or syn.

Just as the members of the groups all follow the same trend, the groups themselves within their respective series also follow a matching trend in that there is an increase in instability and/or bond strain in the order xaa-xx < xas-xx < xsa-xx.

The final trend compares the two series and indicates that members of the sxx-xx series are shifted downwards by about 20 kJ/mol (200 meV) in electronic energy and about 2° in bond angle MAD relative to their respective analogs in the axx-xx series. If the C61-C4 bond is anti, then C3C4 bond is oriented slightly towards the fullerene. Therefore, to alleviate steric issues with the ester group becoming too close to the fullerene, the ^PhC1-C61-C4 bond angle becomes strained in that it decreases from the known value of 115.5° [16] (^PhC1 is used to avoid ambiguity as C1 of the phenyl and C1 of the C₆₀ are both bonded to C61). It decreases to 107.6° for all aaa-xx conformers, 106.9–106.4° for the aas-xx conformers and 103.5–102.7° for the asa-xx conformers. Conversely, if the C61-C4 bond is syn, then the C3-C4 bond is oriented almost vertically away from the fullerene. However, this then brings it closer to the phenyl group. To alleviate similar steric issues with the ester group becoming too close to the phenyl, the ^PhC1-C61-C4 bond angle opens relatively slightly to 115.9–116.3° for the saa-xx conformers, 117.1–117.3° for the aas-xx conformers and 120.0–120.4° for the asa-xx conformers. The average deviation for each group is slightly larger for the axx series than it is for the sxx series, which may explain why the members of the former series have slightly decreasing electronic energies and bond strain MADs. It is also noticed that both these trends in increasing bond strain follow the same xaa-xx < xas-xx < xsa-xx trend for series members, as identified above. Hence, it seems likely that the C61-C4 bond plays a significant role in the conformational behaviour of [60]PCBM, with a strong preference for it being carbon-syn.

3.3. Simulation of the ¹³C NMR Spectra (sp³ Hybridised Carbons)

Based on these analyses, the conformers with the six lowest bond angle strains, as measured by their mean absolute deviations of the relevant bond angles from experiment, were shortlisted to have their ¹³C NMR spectra simulated. These six conformers also had the six lowest electronic energies, and are in order of increasing bond angle MAD, saa-aa, saa-sa, aaa-aa, sas-aa, aaa-as and aaa-sa.

¹³C NMR spectra of the six candidate conformers were simulated. These are presented for the sp³ region, together with the experimental spectrum, in Figure 4. Inspection of these spectra gives a clear indication that only the (b) saa-aa and (c) saa-sa conformations have simulated spectra that can be compared favourably to that of the experimental spectrum. Both follow the experimental line pattern very closely. It is also indicated that saa-sa is the better of the two on groups, having the spacings closer to the experiment. Conversely, both (d) saa-as and (g) sas-aa have the two lines near 50 ppm, much wider spacing than the experiment, and the other three lines are quite evenly spaced rather than having the experimental groupings. Finally, (e) aaa-aa and (f) aaa-sa are the worst of the six shortlisted conformers, with each having the first five lines with reasonably equal spacings.

The observation from the six simulated sp³ NMR spectra that saa-aa and saa-sa are very similar to each other and are the two closest to experiment agrees with the conclusion made earlier from the bond strain and electronic energy analysis. This is because these two conformers have the lowest two bond strains and electronic energies of all the conformers, but their values are very similar. Conversely, of the six simulated spectra, aaa-aa and aaa-sa also appear very similar but give the worst agreement with the experiment. This also accords with the previous analysis, as these have the highest two bond strains and electronic energies of the six shortlisted conformers but are very close to each other in value. That the bond angle MADs (average bond strains), the total electronic energies and the quality of the simulated ¹³C NMR spectra all follow the same trends provides compelling evidence that saa-aa and saa-sa are the two most stable structures for the conformational arrangements of the ester group and are thus the two most occupied conformers.

The discussion above is limited to the sp³ region for two reasons: (1) it is a simple area of the spectrum where comparisons between the different conformers are easy to make, and (2) it involves the very carbons that are relevant to the conformations of the ester (nb., the sp² fullerene and phenyl carbons do not conformationally vary in any of the 24 conformation). Analysis of the far more complicated sp²-hybridised carbons also indicates that saa-sa performed slightly better than saa-aa; for this reason, the saa-as conformer was used in our recent publication on the full spectrum [14].

3.4. Conformational Analysis of the Ester Group

Insights into the dynamical behaviour of the ester group may be obtained with reference to our recent experimental study of second-order spin–spin couplings in the ¹H NMR spectrum. The observed very strong second-order spin–spin couplings at the C4 carbon resulted from restricted rotation about the ester C61-C4 and C4-C3 bonds [12]. For these two bonds, there is gauche-syn/anti-gauche′ and back again restricted rotation. That is, for these two bonds, there is no continued rotation from gauche to gauche′ for steric reasons [12]. Hence, it seems that axx-xx conformers cannot be obtained owing to this restricted rotation. For the same reasons, the xsx-xx conformers also cannot be obtained. This restricted rotation explanation is consistent with the NMR simulations in Figure 4, as these give relatively poor results when the ester is symmetry-constrained into these unfavourable conformations. The poor agreement of the sas-aa conformer’s NMR spectrum with the experiment may also be explained in terms of dynamical behaviour. Although these conformers may be obtained as there is some degree of full rotation about the C2–C3 bond [12], occupation of the syn conformation in this bond should be relatively short lived.

To further investigate these conclusions and extend them to all heavy atom bonds of the ester groups, we conducted a DFT investigation. To this end, we considered the optimised conformer with the lowest total electronic energy and bond strain, (saa-aa)[60]PCBM, to be a “standard” to compare other conformers. This involved re-optimising the geometry of the standard (saa-aa)[60]PCBM so that all bond lengths, bond angles and dihedral angles were fixed, but then the following dihedral angles were each in turn varied from 0° to 180° in 10° steps: (a) ^PhC1-C61-C4-C3, (b) C61-C4-C3-C2, (c) C4-C3-C2-C1, (d) C3-C2-C1-O and (e) C2-C1-O-Me. In this way, plots of relative energy against dihedral angle may be obtained for each of the five heavy-atom dihedral angles of the ester group (Figure 5). The fixing of the bond lengths and angles may be justified under the Born–Oppenheimer approximation. This is because bond length/angle variations are vibrational motion, and these are extremely slow relative to the rotational motion of dihedral angle variation. Hence, bond lengths and bond angles may, to a good approximation, be considered fixed on the time scale of the rotations. These five plots of relative energy against dihedral angle are considered, in turn, below in the abovementioned order.

C61-C4 Bond

A plot of the ^PhC1-C61-C4-C3 dihedral angle (which represents rotation about the C61-C4 bond) against relative energy is presented in Figure 5a. The blue graph is shown at full scale, whereas for clarity, the orange graph is an expansion in energy. This figure reveals two minima at near-gauche and near-gauche’ dihedral angles of +68° and 292° (−68°). The slight variation away from the ideal gauche dihedral angle of 60° is likely to be due to the large asymmetry in the barriers on either side of these minima. The barrier to rotation from gauche to gauche’ via the syn conformer (0°) is 15.3 kJ/mol (176.7 meV), which corresponds to 6.18 × kT at room temperature (RT). A Boltzmann population analysis indicates that about 1 in 500 molecules (0.2%) have enough thermal energy to overcome this barrier. As the barrier is the same height in both directions, the gauche and gauche’ conformers are equally populated.

On the other hand, rotation from gauche to gauche’ via the anti (180°) conformer is impossible, as the barrier is 177 kJ/mol (1.84 eV) or 71.5 × kT RT. A Boltsmann analysis suggests that only 10⁻²⁹% of molecules could overcome this barrier. However, the energy difference between (aaa-aa)[60]PCBM and (saa-aa)[60]PCBM from Figure 3, at 11.6 kJ/mol (120 meV), is much less that that from Figure 5a. A Boltzmann/Arrhenius analysis based on this energy difference suggests that population of the aaa-aa conformer would be slightly less than 1% of that of the saa-aa conformer, and as will be shown for the remaining dihrdral angles, the populations would be far below 1% for the other 11 axx-xx conformers. However, even a 1% population is unlikely to be achieved. This is because the 11.6 kJ/mol energy difference is that of a vibrationally relaxed conformer. As mentioned earlier, with vibrational motions of the bonds (length and angle changes) being about 2 orders of magnitude slower than rotations about the bonds, it can be concluded that the relative population of the aaa-aa conformer is effectively zero. This is because with rotational rapid ascent up the barrier towards aaa-aa along the coordinate of Figure 5a, the configuration would be rapidly repelled from further assent long before it had any opportunity to even start vibrationally relaxing.

Within the gauche and gauche’ conformers about the C61-C4 bond, the ester group undergoes librational behaviour whereby the ^PhC1-C61-C4-C3 dihedral varies between −17° and +14° (gauche) and −14° and +17° (gauche’) either side of the minima, the extremes of which correspond to kT at room temperature (2.48 kJ/mol or 25.7 meV) above the minima in energy.

There are two shoulders on the central peak near 130 and 230 degrees. These are at elevated instability as they occur at dihedral angles about C61-C4 where one or the other of the two hydrogens on C4 is eclipsed with the hydrogen-less ^PhC1 carbon.

It should be noted that the aaa-aa conformer and the saa-aa conformer are related to each other by a rotation of 180° about the C61-C4 bond. As such, they lie on a line through the potential energy surface (PES). Considering the PES along this line while retaining C_S symmetry should show that the aaa-aa conformer is a maximum and saa-sa is a minimum. The saa-aa conformer does not, however, represent the global minimum on the B3LYP/cc-pVTZ PES of (xaa-aa)[60]PCBM. Inspection of Figure 5a shows that the global minimum regarding the relative orientation about the C61-C4 bond has a dihedral angle of about 70°. Confirmation of this comes from an OPT-FREQ calculation that reveals this dihedral angle to be 68.14° with all other relevant dihedrals angles being within a degree of 180°. This structure is lower in energy than the similarly optimised (saa-aa)[60]PCBM structure. In addition, it has no imaginary vibrational frequencies (indicative of a minimum on the PES). However, this structure has C₁ point group symmetry rather than the experimentally observed C_S symmetry. As such, simulations based on this structure in solution would not, in general, resemble the experiment. For example, simulated ¹³C NMR spectra of PCBM would split into 72 resonances instead of the experimentally seen 42 resonances; degenerate energy levels would also be split. As such, it seems likely that the barrier for gauche(’) to syn may be lower than that calculated, and that in reality, the librational motion goes back and forth between 90° and −90° (270°), with the syn conformation (0°) being the centre of the wide motion.

From the analysis of the orientational behaviour about the C61-C4 bond, it can be concluded that none of the 12 axx-xx conformers of [60]PCBM has any significant population. As such, (aaa-aa)[60]PCBM, the most commonly used representation of [60]PCBM in the literature, is essentially energetically forbidden, which suggests that at least some of the many ab initio calculations based on it may have unreliable conclusions.

C4-C3 Bond

The plot of dihedral angle rotation about the C4-C3 bond against relative energy, shown in Figure 5b, indicates that there are three relatively stable conformers, gauche (92°), anti (180°) and gauche’ (272°), and that the syn conformer (0°) at about 75 kJ/mol (~800 meV) represents an unsurmountable barrier (over 30 × kT at RT) to rotation from gauche’ to syn to gauche. This barrier would be much higher (at about 4.2 eV) if the neighbouring C3–C2 dihedral angle was not able to change to partially alleviate the bond strain.

The greater variation away from the ideal gauche angle than that seen for the C61–C4 bond above is due to the even greater asymmetry in the barriers. On this occasion, the barrier for rotation from gauche(’) to anti is 12.18 kJ/mol (126.3 meV, 4.91 × kT at RT), and that to rotate from anti to gauche(’) is 16.32 kJ/mol (169.2 meV, 6.58 × kT at RT).

A Boltzmann analysis based on these barriers indicates that 0.734% of molecules have sufficient thermal energy to overcome the barrier and rotate from the gauche(’) conformers to the anti conformer, and that 0.138% of molecules may similarly rotate from anti to gauche(’). An Arrhenius analysis indicates that there is a 16:84 population ratio of the two conformers, with the anti (180°) conformer being the more favoured. As the barrier to rotation from anti to gauche and that anti to gauche’ are identical, the gauche and gauche’ conformers would be equally populated (at ca. 8% each). These findings are consistent with the conclusion we recently drew on the populations of these three conformers based on well-resolved second-order spin–spin coupling splitting of the hydrogens attached to Carbon C4 by those attached to C3. Based on a CJG conformer analysis, a 12½:75:12½ population ratio for the gauche, anti and gauche’ conformers was estimated [12]. The slight discrepancy might come from imperfect assumptions made in the CJG analysis, in this work, or both. Nevertheless, both this work and our recent CJG estimate from second-order ¹H NMR spin–spin couplings have the general conclusion that the syn conformer is extremely unstable, the anti conformer is the most stable with gauche(’) islands of stability either side of the anti conformer, and that the population ratio of the gauche, anti and gauche’ conformers is about 1:8:1. With the syn conformation being unstable, all xsx-xx conformers have essentially zero population.

Like the ^PhC1-C61-C4-C3 dihedral angle discussed above, there is librational motion about the minima of the gauche, anti and gauche’ conformers. In this case, the librations occur over a 30° range, ±15° either side of the anti conformer (i.e., between C61-C4-C3-C2 dihedral angles of 165°–195°), and over an 18° range, ±9° either side of the gauche(’) conformers (i.e., between dihedral angles of 79°–97° and 263°–181°, respectively).

C3-C2 Bond

A plot of relative electronic energy vs the C4-C3-C2-C1 dihedral angle is given in Figure 5c. Three equal minima are seen at the gauche dihedral angles of −68°, −68° (292°) and at the anti dihedral angle of 180°, with equal gauche-anti and gauche’-anti barriers of 13.4 kJ/mol (140 meV, 5.47 × kT at RT). The more stable 68°, 180° and 292° dihedrals have the hydrogens of C3 and C4 staggered, whereas the unstable 0°, 120° and 240° have those hydrogens eclipsed.

The barrier to rotation through the syn conformer is higher at 21 kJ/mol (220 meV). Like the previously discussed bond, this barrier would be much higher, 155 kJ/mol (1.6 eV) this time, if it wasn’t for the ability of the neighbouring C2–C1 dihedral angle to change and thereby partially alleviate the bond strain. Again, like the previous bond, the syn conformation is unstable compared to the anti conformation, meaning that all xxs-xx conformers also have essentially zero population. An Arrhenius analysis of these barriers suggests that the gauche-anti-gauche’ transition occurs 20 times more often than that of gauche-syn-gauche’. This situation is like that for the C4-C3 bond, where the rest of the ester group “wags” back and forth from gauche to gauche’ via the stable middle conformer (anti in this case) and very rarely by the unstable conformer. However, unlike the ¹H NMR resonances from the hydrogen on carbon C4 being split by those of C3, the NMR spectrum does not indicate significant second-order spin–spin couplings for the hydrogens of carbon C2 being split by those of C3, which we recently interpreted as resulting from near free rotation about the C3-C2 bond [12]. However, this interpretation is not correct. This is because the gauche-anti-gauche’ transition occurring 20 times more often than the gauche-syn-gauche’ transition is inconsistent with free rotation. Therefore, a new explanation is needed of the experimental ¹H NMR observation of a first-order 1:2:1 triplet for the two symmetrically equivalent hydrogens of carbon C2 by those of carbon C3. Instead of “free rotation”, the lack of second-order effects is better explained by the near equal energy barriers for the gauche(’) to anti and the anti to gauche(’) transitions, which would result in near equal populations of the three conformers. This is because at second order, the usual first-order 1:2:1 triplet occurs when the populations of the three staggered conformers about this bond are equal. Hence, is it the effectively equal gauche(’)-anti and anti-gauche(’) barriers, rather than free rotation about the C3-C2 bond, that gives the near equal populations that account for the lack of second-order NMR effects ordinarily expected from non-free rotation.

C2-C1 Bond

From Figure 5d, it is apparent that there are two stable conformers about this bond, syn at 0° and anti at 180°, with the anti conformer being slightly more stable by 0.974 kJ/mol (10.1 meV). The two wells near +30° and −30° (330°) are so shallow, at only 0.19 kJ/mol (2 meV, 0.078 × kT at RT), that they are insignificant in relation to ester dynamics at room temperature.

About the syn conformer, there is librational motion over a very wide range of about 150°. That is, between +75° and −75° (285°). Meanwhile, about the more stable anti conformer, the librational range is only 70°, at ±35° (i.e., between C3-C2-C1-O dihedral angles of 155° and 215°). However, the energy barrier for rotation from anti to syn is far lower than those discussed so far at only 2.2 kT at RT (5.53 kJ/mol, 57.3 meV), and that for syn to anti is even lower at 1.8 kT at RT (4.56 kJ/mol, 47.3 meV). As such, these barriers suggest that there is almost free rotation about this bond. Indeed, a Boltzmann indicates that about 16% of molecules have sufficient thermal energy to rotate from syn to anti at room temperature, and that about 11% of molecules have sufficient energy to rotate the other way. An Arrhenius analysis based on these barriers indicates that there is an approximate 60:40 population ratio of the two conformers with the anti conformer being the more favoured. The much low barriers to full rotation about this bond account for the observation made from Figure 3 that the xxx-aa and xxx-sa conformers, which involve this bond, have the lowest bond strain differences. With this, in simulating molecular spectra of [60]PCBM, it may be advantageous to use a 60:40 weighted average of relevant spectra of (saa-aa)[60]PCBM and (saa-sa)[60]PCBM. For example, Figure 4 h shows a weighted ¹³C NMR spectrum of the sp³-hybridised carbons of [60]PCBM, which is remarkably close to the experimental spectrum (Figure 4a).

C1-O Bond

The final ester bond to have a dihedral angle for heavy elements is the C1-O single bond. The plot of relative electronic energy as a function of the C2-C1-O–Me dihedral angle (Figure 5e) shows three minima near gauche (45°), anti (180°) and gauche’ (−45° or 315°) dihedral angles. However, only the anti conformer is stable, and thereby has any significant population. This is because there is a relatively small barrier of 2.8 kT at RT (6.9 kJ/mol, 72 meV) to gauche(’) to anti rotation, but an essentially unsurmountable barrier of 22.5 kT at RT (53.7 kJ/mol, 577 meV) for the reverse rotation, giving an approximate 1:10⁸:1 population ratio of the gauche, anti and gauche’ conformers. Within the stable anti conformer, there is librational motion about the C1-O bond between dihedral angles of 166° and 194°; i.e., ±14° either side of anti.

4. Conclusions

In summary, the conformational behaviour of the organic electronics n-type material, [60]PCBM, was examined via DFT techniques. This was informed by total electronic energy and average bond strain calculations. With the PhC61 group being conformationally invariant, the relative orientations about the ester bonds C61-C4, C4-C3, C3-C2, C2-C1 and C1-O (which could be either syn or anti to maintain C_S symmetry) gave rise to conformers. There are 24 chemically possible conformers. However, the conformational analysis suggests that only two of them may exit. These had (1) the C61-C4 bond in a syn configuration with all other relevant bonds anti, and (2) both the C61-C4 and C2-C1 bonds in syn configurations with all other relevant bonds being anti (with a respective 60:40 population ratio). With this, there is only reasonably free rotation about the C2-C1 bond of the ester group, with all other bonds suffering from strongly restricted bond rotations owing to steric hindrance from the nearby and bulky fullerene and phenyl groups.

These findings were supported by computational analyses that gave these two conformers, designated (saa-aa)[60]PCBM and (saa-sa)[60]PCBM, as those with the two lowest total electronic energies and the two lowest bond strains. In addition, DFT simulations of the ¹³C spectrum of the ester sp³-hybridised carbons based on these two conformations show a striking resemblance to the experiment, whereas those of other relatively low-energy conformers are barely recognisable in comparison to the experiment. A 60:40 weighted average of ¹³C NMR spectra of these two conformers (reflecting the populations of the two conformers) also gave a spectrum remarkably close to that of the experiment.

A possibly important implication of these findings is they suggest that most representations of [60]PCBM in the literature are unrealistic. This is because they depict the relative orientations about the C61-C4 bond in the particularly unstable anti (180°) conformation. This very commonly depicted anti conformation has the ester group oriented roughly parallel and close to the surface of the fullerene. The much better representation found here is the opposite syn conformation about this bond that has the ester group oriented about perpendicular to the surface. This syn conformation is still consistent with C_S symmetry while being substantially more stable. As such, many published ab initio calculations on this highly important molecule to the field of organic electronics may have employed an improper input geometry with varying degrees of potential repercussions on the validity of the resulting conclusions.

Although [60]PCBM would not maintain C_S symmetry when packed into a solid, the solution-state structure is, nevertheless, highly important to the solid-state structure, as solid [60]PCBM is almost invariably formed from solutions. As such, the conformational conclusions presented here may also provide insights to aid dynamical modelling of the mechanisms of the formation of solution-processed [60]PCBM films.