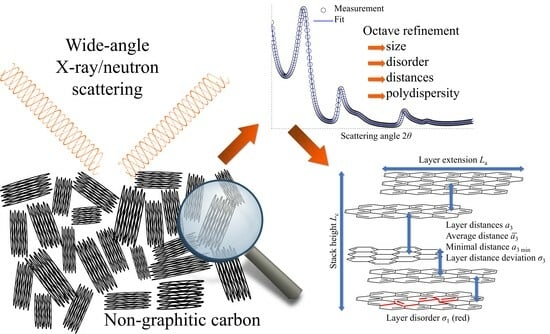
OctCarb—A GNU Octave Script for the Analysis and Evaluation of Wide-Angle Scattering Data of Non-Graphitic Carbons
Abstract
:1. Introduction
2. Materials and Methods
2.1. WAXS/WANS of Non-Graphitic Carbons (NGCs)
= a · (Iinter + Iintra) + b(s)
2.2. Refined Microstructural Parameters
2.2.1. Layer Structure
2.2.2. Interlayer Stacking Structure
2.2.3. Impurities
2.3. Improvements and Implementation in OctCarb
- OctCarb is an entirely free software tool, also with respect to automatic data fitting;
- The data analysis can be performed on average personal computers, i.e., the analysis of one WAXS/WANS curve can be performed within a satisfactory time, i.e., within minutes;
- The tool is resource-efficient in terms of CPU usage, which means that other programs can be run simultaneously;
- Octave and therefore OctCarb is available for Windows, MacOS and Linux;
- Octave provides an option for batch compilation (important for parallel data fitting);
- The program is—in practical details—more convenient than CarbX, e.g., the fitting results (parameters) are now automatically stored;
- No other third-party software tool is needed.
- Wide-angle neutron scattering data can be analyzed;
- A rigorous background treatment (and fitting) for WAXS and WANS, based on the corresponding theoretical contributions (Compton scattering, non-organized carbon, etc.), is included;
- The treatment of impurity atoms (sulfur, nitrogen, etc.) in terms of a contribution to the background scattering was improved;
- The incorporation/treatment of the atomic form factors was optimized;
- The statistical, experimental errors are treated in terms of the well-established theory of error propagation, and calculated based on the covariance matrix, i.e., the standard deviations of the refined parameters are calculated;
- In some cases, the data at the left and right end of the accessible data range are not useable, e.g., because of strong small-angle scattering contributions. The tool contains a comfortable option to skip such data.
2.4. Technical Details and Installation
2.4.1. Third-Party Plugins
2.4.2. Refinement Algorithm
2.4.3. System Requirements and Installation
3. Results
3.1. Usage of OctCarb
3.2. Verification and Application
3.2.1. Software Validation on WAXS Data and General Issues
3.2.2. Influence of the Amount/Noise of Data Points and Start Parameters on the Fitting Routine
3.2.3. Software Validation Using WANS Data
3.2.4. Noise Level Test on WAXS and WANS Data
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Doherty, C.M.; Caruso, R.A.; Smarsly, B.M.; Adelhelm, P.; Drummond, C.J. Hierarchically Porous Monolithic LiFePO 4/Carbon Composite Electrode Materials for High Power Lithium Ion Batteries. Chem. Mater. 2009, 21, 5300–5306. [Google Scholar] [CrossRef]
- Kumar, R.; Dhakate, S.R.; Mathur, R.B. The role of ferrocene on the enhancement of the mechanical and electrochemical properties of coal tar pitch-based carbon foams. J. Mater. Sci. 2013, 48, 7071–7080. [Google Scholar] [CrossRef]
- Oberlin, A. Carbonization and graphitization. Carbon 1984, 22, 521–541. [Google Scholar] [CrossRef]
- Goel, C.; Bhunia, H.; Bajpai, P.K. Synthesis of nitrogen doped mesoporous carbons for carbon dioxide capture. RSC Adv. 2015, 5, 46568–46582. [Google Scholar] [CrossRef]
- Li, J.; Lu, R.; Dou, B.; Ma, C.; Hu, Q.; Liang, Y.; Wu, F.; Qiao, S.; Hao, Z. Porous graphitized carbon for adsorptive removal of benzene and the electrothermal regeneration. Environ. Sci. Technol. 2012, 46, 12648–12654. [Google Scholar] [CrossRef] [Green Version]
- Oschatz, M.; Borchardt, L.; Thommes, M.; Cychosz, K.A.; Senkovska, I.; Klein, N.; Frind, R.; Leistner, M.; Presser, V.; Gogotsi, Y.; et al. Carbide-derived carbon monoliths with hierarchical pore architectures. Angew. Chem. Int. Ed. Engl. 2012, 51, 7577–7580. [Google Scholar] [CrossRef]
- Oschatz, M.; Kockrick, E.; Rose, M.; Borchardt, L.; Klein, N.; Senkovska, I.; Freudenberg, T.; Korenblit, Y.; Yushin, G.; Kaskel, S. A cubic ordered, mesoporous carbide-derived carbon for gas and energy storage applications. Carbon 2010, 48, 3987–3992. [Google Scholar] [CrossRef]
- Silvestre-Albero, A.; Rico-Frances, S.; Rodríguez-Reinoso, F.; Kern, A.M.; Klumpp, M.; Etzold, B.J.; Silvestre-Albero, J. High selectivity of TiC-CDC for CO2/N2 separation. Carbon 2013, 59, 221–228. [Google Scholar] [CrossRef] [Green Version]
- Dash, R.; Chmiola, J.; Yushin, G.; Gogotsi, Y.; Laudisio, G.; Singer, J.; Fischer, J.; Kucheyev, S. Titanium carbide derived nanoporous carbon for energy-related applications. Carbon 2006, 44, 2489–2497. [Google Scholar] [CrossRef] [Green Version]
- Manthiram, A.; Fu, Y.; Chung, S.-H.; Zu, C.; Su, Y.-S. Rechargeable lithium-sulfur batteries. Chem. Rev. 2014, 114, 11751–11787. [Google Scholar] [CrossRef]
- Inagaki, M.; Konno, H.; Tanaike, O. Carbon materials for electrochemical capacitors. J. Power Sources 2010, 195, 7880–7903. [Google Scholar] [CrossRef]
- Oschatz, M.; Borchardt, L.; Pinkert, K.; Thieme, S.; Lohe, M.R.; Hoffmann, C.; Benusch, M.; Wisser, F.M.; Ziegler, C.; Giebeler, L.; et al. Hierarchical Carbide-Derived Carbon Foams with Advanced Mesostructure as a Versatile Electrochemical Energy-Storage Material. Adv. Energy Mater. 2014, 4, 1300645. [Google Scholar] [CrossRef]
- Wang, J.; Sugita, S.; Nagayama, K.; Matsumoto, T. OS18-3 Spatiotemporal Dynamics of Actin during Adhesion Process of MC3T3-E1 Cells to Substrate(Cell and Tissue mechanics 1,OS18 Cell and tissue mechanics, BIOMECHANICS). ATEM 2015, 14, 237. [Google Scholar] [CrossRef]
- Kim, Y.-S.; Guo, X.-F.; Kim, G.-J. Synthesis of carbon monolith with bimodal meso/macroscopic pore structure and its application in asymmetric catalysis. Catal. Today 2010, 150, 91–99. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, L.; Zhou, S.; Zhao, D.; Wu, L. Facile Synthesis of Hierarchically Ordered Porous Carbon via in Situ Self-Assembly of Colloidal Polymer and Silica Spheres and Its Use as a Catalyst Support. Chem. Mater. 2010, 22, 3433–3440. [Google Scholar] [CrossRef]
- Tzeng, S.-S.; Chr, Y.-G. Evolution of microstructure and properties of phenolic resin-based carbon/carbon composites during pyrolysis. Mater. Chem. Phys. 2002, 73, 162–169. [Google Scholar] [CrossRef]
- Perret, R.; Ruland, W. X-ray small-angle scattering of glassy carbon. J. Appl. Crystallogr. 1972, 5, 183–187. [Google Scholar] [CrossRef]
- Fitzer, E.; Kochling, K.-H.; Boehm, H.P.; Marsh, H. Recommended terminology for the description of carbon as a solid (IUPAC Recommendations 1995). Pure Appl. Chem. 1995, 67, 473–506. [Google Scholar] [CrossRef]
- Badaczewski, F.M.; Loeh, M.O.; Pfaff, T.; Dobrotka, S.; Wallacher, D.; Clemens, D.; Metz, J.; Smarsly, B.M. Peering into the structural evolution of glass-like carbons derived from phenolic resin by combining small-angle neutron scattering with an advanced evaluation method for wide-angle X-ray scattering. Carbon 2019, 141, 169–181. [Google Scholar] [CrossRef]
- Badaczewski, F.M.; Loeh, M.O.; Pfaff, T.; Wallacher, D.; Clemens, D.; Smarsly, B.M. An advanced structural characterization of templated meso-macroporous carbon monoliths by small- and wide-angle scattering techniques. Beilstein J. Nanotechnol. 2020, 11, 310–322. [Google Scholar] [CrossRef]
- Faber, K.; Badaczewski, F.M.; Oschatz, M.; Mondin, G.; Nickel, W.; Kaskel, S.; Smarsly, B.M. In-Depth Investigation of the Carbon Microstructure of Silicon Carbide-Derived Carbons by Wide-Angle X-ray Scattering. J. Phys. Chem. C 2014, 118, 15705–15715. [Google Scholar] [CrossRef]
- Faber, K.; Badaczewski, F.M.; Ruland, W.; Smarsly, B.M. Investigation of the Microstructure of Disordered, Non-graphitic Carbons by an Advanced Analysis Method for Wide-Angle X-ray Scattering. Z. Anorg. Allg. Chem. 2014, 640, 3107–3117. [Google Scholar] [CrossRef]
- Loeh, M.O.; Badaczewski, F.M.; Faber, K.; Hintner, S.; Bertino, M.F.; Mueller, P.; Metz, J.; Smarsly, B.M. Analysis of thermally induced changes in the structure of coal tar pitches by an advanced evaluation method of X-ray scattering data. Carbon 2016, 109, 823–835. [Google Scholar] [CrossRef]
- Loeh, M.O.; Badaczewski, F.M.; von der Lehr, M.; Ellinghaus, R.; Dobrotka, S.; Metz, J.; Smarsly, B.M. Hard-templating of carbon using porous SiO2 monoliths revisited—Quantitative impact of spatial confinement on the microstructure evolution. Carbon 2018, 129, 552–563. [Google Scholar] [CrossRef]
- Pfaff, T.; Simmermacher, M.; Smarsly, B.M. CarbX: A program for the evaluation of wide-angle X-ray scattering data of non-graphitic carbons. J. Appl. Crystallogr. 2018, 51, 219–229. [Google Scholar] [CrossRef] [Green Version]
- Pfaff, T.; Badaczewski, F.M.; Loeh, M.O.; Franz, A.; Hoffmann, J.-U.; Reehuis, M.; Zeier, W.G.; Smarsly, B.M. Comparative Microstructural Analysis of Nongraphitic Carbons by Wide-Angle X-ray and Neutron Scattering. J. Phys. Chem. C 2019, 123, 20532–20546. [Google Scholar] [CrossRef]
- Ou, M.; Zhang, Y.; Zhu, Y.; Fan, C.; Sun, S.; Feng, J.; Sun, X.; Wei, P.; Xu, J.; Peng, J.; et al. Local Structures of Soft Carbon and Electrochemical Performance of Potassium-Ion Batteries. ACS Appl. Mater. Interfaces 2021, 13, 28261–28269. [Google Scholar] [CrossRef]
- Härmas, R.; Palm, R.; Kurig, H.; Puusepp, L.; Pfaff, T.; Romann, T.; Aruväli, J.; Tallo, I.; Thomberg, T.; Jänes, A.; et al. Carbide-Derived Carbons: WAXS and Raman Spectra for Detailed Structural Analysis. C 2021, 7, 29. [Google Scholar] [CrossRef]
- Schüpfer, D.B.; Badaczewski, F.M.; Guerra-Castro, J.M.; Hofmann, D.M.; Heiliger, C.; Smarsly, B.M.; Klar, P.J. Assessing the structural properties of graphitic and non-graphitic carbons by Raman spectroscopy. Carbon 2020, 161, 359–372. [Google Scholar] [CrossRef]
- Schüpfer, D.B.; Badaczewski, F.M.; Peilstöcker, J.; Guerra-Castro, J.M.; Shim, H.; Firoozabadi, S.; Beyer, A.; Volz, K.; Presser, V.; Heiliger, C.; et al. Monitoring the thermally induced transition from sp3-hybridized into sp2-hybridized carbons. Carbon 2021, 172, 214–227. [Google Scholar] [CrossRef]
- Shi, H.; Reimers, J.N.; Dahn, J.R. Structure-refinement program for disordered carbons. J. Appl. Crystallogr. 1993, 26, 827–836. [Google Scholar] [CrossRef]
- Tsui, L. CarbonXS GUI. Available online: https://lktsui.github.io/carbon_xs_gui/tutorial.html (accessed on 4 January 2021).
- Tsui, L.; Garzon, F. CarbonXS GUI: A graphical front-end for CarbonXS. J. Appl. Crystallogr. 2017, 50, 1830–1833. [Google Scholar] [CrossRef]
- Fujimoto, H.; Shiraishi, M. Characterization of unordered carbon using Warren–Bodenstein’s equation. Carbon 2001, 39, 1753–1761. [Google Scholar] [CrossRef]
- Fujimoto, H. Theoretical X-ray scattering intensity of carbons with turbostratic stacking and AB stacking structures. Carbon 2003, 41, 1585–1592. [Google Scholar] [CrossRef]
- Fujimoto, H. A new estimation method for the degree of graphitization for random layer lattices. Carbon 2010, 48, 3446–3453. [Google Scholar] [CrossRef]
- Warren, B.E.; Bodenstein, P. The diffraction pattern of fine particle carbon blacks. Acta Cryst. 1965, 18, 282–286. [Google Scholar] [CrossRef] [Green Version]
- Fujimoto, H. Carbon Analyzer, 2022. Available online: http://www.asahi-net.or.jp/~qn6h-fjmt (accessed on 2 November 2022).
- Saenko, N.S. The X-ray diffraction study of three-dimensional disordered network of nanographites: Experiment and theory. Phys. Procedia 2012, 23, 102–105. [Google Scholar] [CrossRef] [Green Version]
- Dopita, M.; Rudolph, M.; Salomon, A.; Emmel, M.; Aneziris, C.G.; Rafaja, D. Simulations of X-Ray Scattering on Two-Dimensional, Graphitic and Turbostratic Carbon Structures. Adv. Eng. Mater. 2013, 15, 1280–1291. [Google Scholar] [CrossRef]
- Dopita, M.; Emmel, M.; Salomon, A.; Rudolph, M.; Matěj, Z.; Aneziris, C.G.; Rafaja, D. Temperature evolution of microstructure of turbostratic high melting coal-tar synthetic pitch studied using wide-angle X-ray scattering method. Carbon 2015, 81, 272–283. [Google Scholar] [CrossRef]
- MATLAB, Version 9.9.0 (R2020b); The MathWorks Inc.: Natick, MA, USA, 2020.
- Ungár, T.; Gubicza, J.; Ribárik, G.; Pantea, C.; Zerda, T. Microstructure of carbon blacks determined by X-ray diffraction profile analysis. Carbon 2002, 40, 929–937. [Google Scholar] [CrossRef]
- Ruland, W.; Smarsly, B.M. X-ray scattering of non-graphitic carbon: An improved method of evaluation. J. Appl. Crystallogr. 2002, 35, 624–633. [Google Scholar] [CrossRef]
- Wolfram Research, Inc. Mathematica, Version 12.1, 2020. Available online: https://www.wolfram.com/mathematica (accessed on 2 November 2022).
- Eaton, J.W.; Bateman, D.; Hauberg, S.; Wehbring, R. {GNU Octave} Version 5.2.0 Manual: A High-Level Interactive Language for Numerical Computations, 2020. Available online: https://www.gnu.org/software/octave/doc/v5.2.0/ (accessed on 2 November 2022).
- Free Software Foundation, Inc. GNU General Public License: Version 3. Available online: https://www.gnu.org/licenses/gpl-3.0.html (accessed on 21 October 2020).
- Warren, B.E. X-Ray Diffraction in Random Layer Lattices. Phys. Rev. 1941, 59, 693–698. [Google Scholar] [CrossRef]
- Biscoe, J.; Warren, B.E. An X-Ray Study of Carbon Black. J. Appl. Phys. 1942, 13, 364–371. [Google Scholar] [CrossRef]
- Scherrer, P. Bestimmung der inneren Struktur und der Größe von Kolloidteilchen mittels Röntgenstrahlen. In Kolloidchemie ein Lehrbuch; Zsigmondy, R., Ed.; Springer: Berlin/Heidelberg, Germany, 1912; pp. 387–409. ISBN 978-3-662-33517-8. [Google Scholar]
- Sharma, A.; Kyotani, T.; Tomita, A. Comparison of structural parameters of PF carbon from XRD and HRTEM techniques. Carbon 2000, 38, 1977–1984. [Google Scholar] [CrossRef]
- Diamond, R. X-ray studies of some carbonized coals. Phil. Trans. R. Soc. Lond. A 1960, 252, 193–223. [Google Scholar] [CrossRef]
- Perret, R.; Ruland, W. Profile analysis of random-layer lines. J. Appl. Crystallogr. 1968, 1, 257–262. [Google Scholar] [CrossRef]
- Ruland, W. X-ray studies on the carbonization and graphitization of acenaphthylene and bifluorenyl. Carbon 1965, 2, 365–378. [Google Scholar] [CrossRef]
- Ruland, W. Fourier transform methods for random-layer line profiles. Acta Cryst. 1967, 22, 615–623. [Google Scholar] [CrossRef]
- Houska, C.R.; Warren, B.E. X-Ray Study of the Graphitization of Carbon Black. J. Appl. Phys. 1954, 25, 1503–1509. [Google Scholar] [CrossRef]
- Franklin, R.E. The interpretation of diffuse X-ray diagrams of carbon. Acta Cryst. 1950, 3, 107–121. [Google Scholar] [CrossRef]
- Franklin, R.E. Crystallite growth in graphitizing and non-graphitizing carbons. Proc. R. Soc. Lond. A 1951, 209, 196–218. [Google Scholar] [CrossRef]
- Prince, E.; Fuess, H.; Hahn, T.; Wondratschek, H.; Müller, U.; Shmueli, U.; Authier, A.; Kopský, V.; Litvin, D.B.; Rossmann, M.G.; et al. International Tables for Crystallography; International Union of Crystallography: Chester, UK, 2006; ISBN 978-1-4020-5259-0. [Google Scholar]
- octave.org. Preface (GNU Octave (Version 5.2.0)). Available online: https://octave.org/doc/v5.2.0/Preface.html (accessed on 2 November 2021).
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Quart. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef] [Green Version]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Moré, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. In Numerical Analysis; Watson, G.A., Ed.; Springer: Berlin/Heidelberg, Germany, 1978; pp. 105–116. ISBN 978-3-540-08538-6. [Google Scholar]
- Vetterling, W.T. Numerical Recipes, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007; ISBN 0521880688. [Google Scholar]
- Einert, M.; Wessel, C.; Badaczewski, F.; Leichtweiß, T.; Eufinger, C.; Janek, J.; Yuan, J.; Antonietti, M.; Smarsly, B.M. Nitrogen-Doped Carbon Electrodes: Influence of Microstructure and Nitrogen Configuration on the Electrical Conductivity of Carbonized Polyacrylonitrile and Poly(ionic liquid) Blends. Macromol. Chem. Phys. 2015, 216, 1930–1944. [Google Scholar] [CrossRef]
- Holleman, A.F.; Wiberg, E.; Wiberg, N.; Fischer, G. Anorganische Chemie; 103. Auflage; De Gruyter: Berlin, Boston, 2017; ISBN 978-3-11-051854-2. [Google Scholar]
- Strunz, H. Strunz Mineralogical Tables. Ninth Edition: Chemical-Structural Mineral Classification System, 9th ed.; Schweizerbart: Stuttgart, Germany, 2020; ISBN 9783510654529. [Google Scholar]
- Hoffmann, J.-U.; Reehuis, M. E2: The Flat-Cone Diffractometer at BER II. JLSRF 2018, 4, A129. [Google Scholar] [CrossRef] [Green Version]
- Ruland, W.; Tompa, H. The effect of multiple scattering on structural parameters determined from X-ray small-angle scattering. J. Appl. Crystallogr. 1972, 5, 1–7. [Google Scholar] [CrossRef]
- Warren, B.E.; Bodenstein, P. The shape of two-dimensional carbon black reflections. Acta Cryst. 1966, 20, 602–605. [Google Scholar] [CrossRef]
- Masson, O.; Thomas, P. Exact and explicit expression of the atomic pair distribution function as obtained from X-ray total scattering experiments. J. Appl. Crystallogr. 2013, 46, 461–465. [Google Scholar] [CrossRef]
- Olds, D.P.; Duxbury, P.M. Efficient algorithms for calculating small-angle scattering from large model structures. J. Appl. Crystallogr. 2014, 47, 1077–1086. [Google Scholar] [CrossRef]
- HKHLR—HPC Hessen. justHPC Gießen. Available online: https://www.hkhlr.de/de/cluster/justhpc-giessen (accessed on 21 July 2022).
- Placzek, G. The Scattering of Neutrons by Systems of Heavy Nuclei. Phys. Rev. 1952, 86, 377–388. [Google Scholar] [CrossRef]
- Fischer, H.E.; Barnes, A.C.; Salmon, P.S. Neutron and x-ray diffraction studies of liquids and glasses. Rep. Prog. Phys. 2006, 69, 233–299. [Google Scholar] [CrossRef]
- Milberg, M.E.; Brailsford, A.D. The atomic incoherent scattering intensities of boron, oxygen and carbon. Acta Cryst. 1958, 11, 672–673. [Google Scholar] [CrossRef]
- Keating, D.T.; Vineyard, G.H. The complete incoherent scattering function for carbon. Acta Cryst. 1956, 9, 895–896. [Google Scholar] [CrossRef]
- Ruland, W. X-ray determination of crystallinity and diffuse disorder scattering. Acta Cryst. 1961, 14, 1180–1185. [Google Scholar] [CrossRef]
- James, R.W. The Optical Principles of the Diffraction of X-rays; George Bell & Sons: London, UK, 1962; Volume 2. [Google Scholar]
- Ruland, W. The separation of coherent and incoherent Compton X-ray scattering. Br. J. Appl. Phys. 1964, 15, 1301–1307. [Google Scholar] [CrossRef]
- Buerger, M.J. The Correction of X-Ray Diffraction Intensities for Lorentz and Polarization Factors. Proc. Natl. Acad. Sci. USA 1940, 26, 637–642. [Google Scholar] [CrossRef] [Green Version]
- Schulz, L.G. A Direct Method of Determining Preferred Orientation of a Flat Reflection Sample Using a Geiger Counter X-Ray Spectrometer. J. Appl. Phys. 1949, 20, 1030–1033. [Google Scholar] [CrossRef]
- Sivia, D.S. Elementary Scattering Theory: For X-ray and Neutron Users; Reprinted; Oxford University Press: Oxford, UK, 2017; ISBN 9780199228683. [Google Scholar]
- Hubbell, J.H.; Seltzer, S. Tables of X-Ray Mass Attenuation Coefficients and Mass Energy-Absorption Coefficients 1 keV to 20 MeV for Elements Z = 1 to 92 and 48 Additional Substances of Dosimetric Interest. 1995. Available online: https://www.semanticscholar.org/paper/Tables-of-X-Ray-Mass-Attenuation-Coefficients-and-1-Hubbell-Seltzer/2098301d7be3283817f2567a2c5ca4553b5b41a8 (accessed on 2 November 2022).
- NIST Center for Neutron Research. Neutron Scattering Lengths and Cross Sections. Available online: https://www.ncnr.nist.gov/resources/n-lengths/ (accessed on 2 November 2022).
- Fox, A.G.; O’Keefe, M.A.; Tabbernor, M.A. Relativistic Hartree–Fock X-ray and electron atomic scattering factors at high angles. Acta Crystallogr. A Found Crystallogr. 1989, 45, 786–793. [Google Scholar] [CrossRef] [Green Version]
- Sears, V.F. Neutron scattering lengths and cross sections. Neutron News 1992, 3, 26–37. [Google Scholar] [CrossRef]
- Cromer, D.T. Compton Scattering Factors for Aspherical Free Atoms. J. Chem. Phys. 1969, 50, 4857–4859. [Google Scholar] [CrossRef]
- Salmon, P.S.; Petri, I. Structure of glassy and liquid GeSe 2. J. Phys. Condens. Matter 2003, 15, S1509–S1528. [Google Scholar] [CrossRef]








| Parameter | Description | Explanation |
|---|---|---|
| La | Average graphene layer size |  |
| lm κa | Average chord length of layers Polydispersity of layers |  |
| lcc σ1 | Average C-C bond length Intralayer disorder |  |
| Parameter | Description | Explanation |
|---|---|---|
| Lc κc | Average stack height Polydispersity of stack height |  |
a3 min σ3 N | Average layer distance Minimal layer distance Standard deviation of layer distances Average number of layers per Stack |  |
| η | Homogeneity of the stacks |  |
| q | Preferred orientation |  |
| Δan | Anisotropy for the atomic form factor of carbon |  |
| Parameter | Description | Explanation |
|---|---|---|
| cun cH cN cO cS | Concentration of unorganized carbon Concentration of unorganized hydrogen Concentration of unorganized nitrogen Concentration of unorganized oxygen Concentration of unorganized sulfur |  |
| Perf. WAXS Data | Noisy WAXS Data | Perf. WANS Data | Noisy WANS Data | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | Input | Fit | Error | Fit | Error | Fit | Error | Fit | Error |
| 3.70 | 3.70 | 0.0% | 3.69 | −0.3% | 3.70 | 0.0% | 3.69 | −0.3% | |
| σ3 | 0.50 | 0.50 | 0.0% | 0.49 | −2.0% | 0.50 | 0.0% | 0.46 | −8.0% |
| N | 3.0 | 3.0 | 0.0% | 3.0 | 0.0% | 3.0 | 0.0% | 3.0 | 0.0% |
| Lc | 11.1 | 11.1 | 0.0% | 11.1 | 0.0% | 11.1 | 0.0% | 11.10 | 0.0% |
| κc | 0.50 | 0.50 | 0.0% | 0.50 | 0.0% | 0.50 | 0.0% | 0.52 | 4.0% |
| La | 20.0 | 20.0 | 0.0% | 20.0 | 0.0% | 20.0 | 0.0% | 20.00 | 0.0% |
| lcc | 1.420 | 1.420 | 0.0% | 1.419 | −0.1% | 1.420 | 0.0% | 1.420 | 0.0% |
| σ1 | 0.025 | 0.030 | 20.0% | 0.016 | −36.0% | 0.025 | 0.0% | 0.025 | 0.0% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Osswald, O.; Smarsly, B.M. OctCarb—A GNU Octave Script for the Analysis and Evaluation of Wide-Angle Scattering Data of Non-Graphitic Carbons. C 2022, 8, 78. https://doi.org/10.3390/c8040078
Osswald O, Smarsly BM. OctCarb—A GNU Octave Script for the Analysis and Evaluation of Wide-Angle Scattering Data of Non-Graphitic Carbons. C. 2022; 8(4):78. https://doi.org/10.3390/c8040078
Chicago/Turabian StyleOsswald, Oliver, and Bernd M. Smarsly. 2022. "OctCarb—A GNU Octave Script for the Analysis and Evaluation of Wide-Angle Scattering Data of Non-Graphitic Carbons" C 8, no. 4: 78. https://doi.org/10.3390/c8040078
APA StyleOsswald, O., & Smarsly, B. M. (2022). OctCarb—A GNU Octave Script for the Analysis and Evaluation of Wide-Angle Scattering Data of Non-Graphitic Carbons. C, 8(4), 78. https://doi.org/10.3390/c8040078