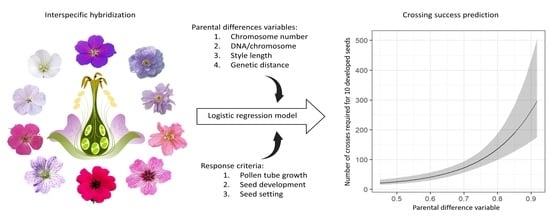
Prediction Model for Breeding Hardy Geraniums
Abstract
:1. Introduction
2. Materials and Methods
2.1. Plant Material and Growing Conditions
2.2. Parental Difference
2.3. Crossing Success Criteria
- (1)
- Pollen tube growth (tube_length) using aniline blue staining tests (see further);
- (2)
- Seed development (seed_dev) is defined as the percentage of crossed flowers with at least one swollen ovule with white, yellow, or green testa or mature seed with brown testa, 7–35 days after pollination (for 2021);
- (3)
- Seed set (seed_set) as the percentage of crossed flowers with at least one mature seed with brown testa, 25–35 days after pollination (for 2020).
2.4. Statistical Analysis
3. Results
3.1. Pre-Zygotic and Post-Zygotic Barriers
3.2. Prediction of Crossing Success
3.3. Prediction of Required Cross Number to Have 10 Crossing Products
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aedo, C. Taxonomic Revision of Geranium Sect. Brasiliensia (Geraniaceae). Syst. Bot. 2001, 26, 205–215. [Google Scholar] [CrossRef]
- Yeo, P.F. Hardy Geraniums; Batsford: London, UK, 2001; ISBN 0713485000. [Google Scholar]
- Van Huylenbroeck, J.; Eeckhaut, T.; Leus, L.; Van Laere, K.; Dhooghe, E. Bridging the Gap: Tools for Interspecific and Intergeneric Hybridization in Ornamentals. In Proceedings of the XXVI International Eucarpia Symposium Section Ornamentals: Editing Novelty 1283, Erfurt, Germany, 1–4 September 2019; pp. 161–168. [Google Scholar] [CrossRef]
- Lewis, M.; Chappell, M.; Thomas, P.A.; Maynard, R.C.; Greyvenstein, O. Development and Verification of an Interspecific Hybridization Protocol for Asclepias. HortScience 2021, 56, 831–837. [Google Scholar] [CrossRef]
- Yue, Y.; Ruter, J.M. Pavonia 3rufula (Malvaceae): An Interspecific Hybrid between Pavonia lasiopetala and Pavonia missionum. HortScience 2021, 56, 732–735. [Google Scholar] [CrossRef]
- Do Nascimento, N.F.F.; Do Rêgo, E.R.; Nascimento, M.F.; Bruckner, C.H.; Finger, F.L.; Do Rêgo, M.M. Evaluation of Production and Quality Traits in Interspecific Hybrids of Ornamental Pepper. Hortic. Bras. 2019, 37, 315–323. [Google Scholar] [CrossRef] [Green Version]
- Blakeslee, A.F. Removing Some of the Barriers to Crossability in Plants. Proc. Am. Philos. Soc. 1945, 89, 561–574. [Google Scholar]
- Dresselhaus, T.; Franklin-Tong, N. Male-Female Crosstalk during Pollen Germination, Tube Growth and Guidance, and Double Fertilization. Mol. Plant 2013, 6, 1018–1036. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hiscock, S.J.; Allen, A.M. Diverse Cell Signalling Pathways Regulate Pollen-stigma Interactions: The Search for Consensus. New Phytol. 2008, 179, 286–317. [Google Scholar] [CrossRef]
- Heslop-Harrison, Y.; Shivanna, K.R. The Receptive Surface of the Angiosperm Stigma. Ann. Bot. 1977, 41, 1233–1258. [Google Scholar] [CrossRef] [Green Version]
- Heslop-Harrison, Y. Control Gates and Micro-Ecology: The Pollen-Stigma Interaction in Perspective. Ann. Bot. 2000, 85 (Suppl. S1), 5–13. [Google Scholar] [CrossRef] [Green Version]
- Zinkl, G.M.; Zwiebel, B.I.; Grier, D.G.; Preuss, D. Pollen-Stigma Adhesion in Arabidopsis: A Species-Specific Interaction Mediated by Lipophilic Molecules in the Pollen Exine. Development 1999, 126, 5431–5440. [Google Scholar] [CrossRef]
- Tupý, J. Callose Formation in Pollen Tubes and Incompatibility. Biol. Plant. Prague 1959, 1, 192–198. [Google Scholar] [CrossRef]
- Mulcahy, D.L. Models of Pollen Tube Competition in Geranium Maculatum. In Pollination Biology; Elsevier Science & Technology Books: Amsterdam, The Netherlands, 1983; pp. 151–161. ISBN 0125839804. [Google Scholar]
- Hessing, M.B. Differential Pollen Tube Success in Geranium caespitosum. Bot. Gaz. 1989, 150, 404–410. [Google Scholar] [CrossRef]
- Sahoo, J.P.; Mohapatra, P.P.; Acharya, L.K.; Jena, C. Insights into the Embryo Rescue-a Modern in-Vitro Crop Improvement Approach in Horticulture. Plant Cell Biotechnol. Mol. Biol. 2021, 22, 20–33. [Google Scholar]
- Shen, X.; Gmitter, F.G.; Grosser, J.W. Immature Embryo Rescue and Culture. In Plant Embryo Culture: Methods and Protocols; Thorpe, T.A., Yeung, E.C., Eds.; Humana Press: Totowa, NJ, USA, 2011; pp. 75–92. ISBN 978-1-61737-988-8. [Google Scholar] [CrossRef]
- Lafon-Placette, C.; Johannessen, I.M.; Hornslien, K.S.; Ali, M.F.; Bjerkan, K.N.; Bramsiepe, J.; Glöckle, B.M.; Rebernig, C.A.; Brysting, A.K.; Grini, P.E. Endosperm-Based Hybridization Barriers Explain the Pattern of Gene Flow between Arabidopsis lyrata and Arabidopsis arenosa in Central Europe. Proc. Natl. Acad. Sci. USA 2017, 114, E1027–E1035. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giancaspro, A.; Mazzeo, A.; Carlomagno, A.; Gadaleta, A.; Somma, S.; Ferrara, G. Optimization of an In Vitro Embryo Rescue Protocol for Breeding Seedless Table Grapes (Vitis Vinifera L.) in Italy. Horticulturae 2022, 8, 121. [Google Scholar] [CrossRef]
- Bhatia, R.; Dey, S.S.; Sharma, K.; Singh, S.; Kumar, S.; Pramanik, A.; Parkash, C.; Kumar, R. Back-Cross Introgression of ‘Tour’ Cytoplasm from Brassica napus through in Vitro Embryo Rescue Reveals Partial Restoration of Sterility in B. oleracea. Sci. Hortic. 2021, 282, 110014. [Google Scholar] [CrossRef]
- Stewart, J.M. In Vitro Fertilization and Embryo Rescue. Environ. Exp. Bot. 1981, 21, 301–315. [Google Scholar] [CrossRef]
- Stelkens, R.; Seehausen, O. Genetic Distance between Species Predicts Novel Trait Expression in Their Hybrids. Evolution 2009, 63, 884–897. [Google Scholar] [CrossRef] [Green Version]
- Granados Mendoza, C.; Wanke, S.; Goetghebeur, P.; Samain, M.S. Facilitating Wide Hybridization in Hydrangea s. l. Cultivars: A Phylogenetic and Marker-Assisted Breeding Approach. Mol. Breed. 2013, 32, 233–239. [Google Scholar] [CrossRef]
- Denaeghel, H.; Van Laere, K.; Leus, L.; Van Huylenbroeck, J.; Van Labeke, M.-C. Interspecific Hybridization in Sarcococca Supported by Analysis of Ploidy Level, Genome Size and Genetic Relationships. Euphytica 2017, 213, 149. [Google Scholar] [CrossRef]
- Dhooghe, E.; Sparke, J.; Oenings, P.; Van Paemel, T.; Van Labeke, M.-C.; Winkelmann, T. Helleborus. In Ornamental Crops; Van Huylenbroeck, J., Ed.; Springer International Publishing: Cham, Switzerland, 2018; pp. 439–452. ISBN 978-3-319-90698-0. [Google Scholar] [CrossRef]
- Akbarzadeh, M.; Van Laere, K.; Leus, L.; De Riek, J.; Van Huylenbroeck, J.; Werbrouck, S.P.O.; Dhooghe, E. Can Knowledge of Genetic Distances, Genome Sizes and Chromosome Numbers Support Breeding Programs in Hardy Geraniums? Genes 2021, 12, 730. [Google Scholar] [CrossRef] [PubMed]
- Chung, N.C.; Miasojedow, B.; Startek, M.; Gambin, A. Jaccard/Tanimoto Similarity Test and Estimation Methods for Biological Presence-Absence Data. BMC Bioinform. 2019, 20, 644. [Google Scholar] [CrossRef] [PubMed]
- McCullagh, P.; Nelder, J.A. Generalized Linear Models; Chapman and Hall: London, UK, 1989. [Google Scholar] [CrossRef]
- Venables, W.N.; Ripley, B.D. Random and mixed effects. In Modern Applied Statistics with S; Venables, W.N., Ripley, B.D., Eds.; Springer: New York, NY, USA, 2002; pp. 271–300. ISBN 978-0-387-21706-2. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013; Available online: https://www.R-project.org/ (accessed on 15 April 2023).
- Lenth, R.; Lenth, M.R. Package ‘Emmeans’. Statistician 2017, 34, 216–221. [Google Scholar]
- Wickham, H. Data analysis. In ggplot2: Elegant Graphics for Data Analysis; Wickham, H., Ed.; Springer International Publishing: Cham, Switzerland, 2016; pp. 189–201. ISBN 978-3-319-24277-4. [Google Scholar] [CrossRef]
- Parton, E. Flower Biology and Crossing Barriers in Bromeliaceae. Ph.D. Thesis, Katholieke Universiteit, Leuven, Belgium, 2001. [Google Scholar]
- Dhooghe, E.; Reheul, D.; Van Labeke, M.-C. Overcoming Pre-Fertilization Barriers in Intertribal Crosses between Anemone coronaria L. and Ranunculus asiaticus L. Horticulturae 2021, 7, 529. [Google Scholar] [CrossRef]
- Dumas, C.; Knox, R.B. Callose and Determination of Pistil Viability and Incompatibility. Theor. Appl. Genet. 1983, 67, 1–10. [Google Scholar] [CrossRef]
- Parre, E.; Geitmann, A. More than a Leak Sealant. The Mechanical Properties of Callose in Pollen Tubes. Plant Physiol. 2005, 137, 274–286. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.-Q.; Moscatelli, A.; Cai, G.; Cresti, M. Functional Interactions among Cytoskeleton, Membranes, and Cell Wall in the Pollen Tube of Flowering Plants. Int. Rev. Cytol. 1997, 176, 133–199. [Google Scholar] [CrossRef]
- Qin, P.; Ting, D.; Shieh, A.; McCormick, S. Callose Plug Deposition Patterns Vary in Pollen Tubes of Arabidopsis thaliana ecotypes and Tomato Species. BMC Plant Biol. 2012, 12, 178. [Google Scholar] [CrossRef] [Green Version]
- Snow, A.A.; Spira, T.P. Differential Pollen-tube Growth Rates and Nonrandom Fertilization in Hibiscus moscheutos (Malvaceae). Am. J. Bot. 1991, 78, 1419–1426. [Google Scholar] [CrossRef] [Green Version]
- Van Tuyl, J.M.; Lim, K.-B. Interspecific Hybridisation and Polyploidisation as Tools in Ornamental Plant Breeding. In Proceedings of the XXI International Eucarpia Symposium on Classical versus Molecular Breeding of Ornamentals—Part I 612, München, Germany, 25–29 August 2003; pp. 13–22. [Google Scholar] [CrossRef]
- Van Tuyl, J.M.; De Jeu, M.J. Methods for overcoming interspecific crossing barriers. In Pollen Biotechnology for Crop Production and Improvement; Cambridge University Press: New York, NY, USA, 1997; pp. 273–292. [Google Scholar]
- Van Tuyl, J.M.; Maas, I.W.G.M.; Lim, K.-B. Introgression in Interspecific Hybrids of Lily. In Proceedings of the VIII International Symposium on Flowerbulbs 570, Cape Town, South Africa, 28 August 2000; pp. 213–218. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.; Deng, M. Geraniaceae. In Identification and Control of Common Weeds: Volume 2; Springer: Dordrecht, The Netherlands, 2017; pp. 629–637. [Google Scholar] [CrossRef]
- Boesewinkel, F.D.; Been, W. Development of Ovule and Testa of Geranium pratense L. and Some Other Representatives of the Geraniaceae. Acta Bot. Neerl. 1979, 28, 335–348. [Google Scholar] [CrossRef]
- Plaschil, S.; Budahn, H.; Klocke, E.; Wiedemann, M.; Olbricht, K. Spontaneous Polyploidisation of Interspecific and Intersectional Pelargonium Hybrids during Embryo Rescue. J. Appl. Bot. Food Qual. 2021, 94, 206–212. [Google Scholar] [CrossRef]
- Denis-Peixoto, L.; Cadic, A.; Renou, J.-P. Interspecific Crosses between Pelargonium × Hortorum and P. quinquelobatum Using Embryo Rescue and Molecular Characterization of Hybrids by an Endogenous Chs Probe. Plant Breed. 1997, 116, 177–180. [Google Scholar] [CrossRef]




| Codes | Genotypes | Subgenera | Parents |
|---|---|---|---|
| G01 | G. ‘Anne Thomson’ | Geranium | Parent 1: G. procurrens, Parent 2: G. psilostemon |
| G02 | G. ‘Azure rush’ | Geranium | Parent 1: G. wallichianum, Parent 2: G. ‘Rozanne’ |
| G03 | G. ‘Bob’s Blunder’ | Geranium | unknown |
| G04 | G. ‘Brookside’ | Geranium | Parent 1: G. pretense, Parent 2: G. clarkei |
| G05 | G. ‘Catherine Deneuve’ | Geranium | Parent 1: G. psilostemon, Parent 2: G. × oxonianum or G.procurrens |
| G06 | G. ‘Chantilly’ | Geranium | Parent 1: G. gracile, Parent 2: G. renardii |
| G07 | G. ‘Dragon Heart’ | Geranium | Parent 1: G. psilostemon, Parent 2: G. procurrens |
| G09 | G. pratense ‘Galactic’ | Geranium | G. pratense |
| G10 | G. cinereum ‘Jolly Jewel Red’ | Erodioidea | G. cinereum |
| G13 | G. × riversleaianum ‘Mavis Simpson’ | Geranium | Parent 1: G. endressii, Parent 2: G. traversii |
| G14 | G. ‘Orion’ | Geranium | Parent 1: G. ‘Brookside’, Parent 2: G. himalayense |
| G16 | G. ‘Rozanne’ | Geranium | Parent 1: G. wallichianum, Parent 2: G. himalayense |
| G17 | G. ‘Salome’ | Geranium | Parent 1: G. lambertii × G. procurrens, Parent 2: G. sanguineum |
| G18 | G. ‘Sanne’ | Geranium | Parent 1: G. sessiliflorum, Parent 2: G. × oxonianum |
| G19 | G. nodosum ‘Silverwood’ | Geranium | G. nodosum |
| G21 | G. wallichianum ‘Sylvia’s Surprise’ | Geranium | G. wallichianum |
| G22 | G. ‘Tanya Rendall’ | Geranium | G. × antipodeum |
| G24 | G. ‘Tiny Monster’ | Geranium | Parent 1: G. sanguineum, Parent 2: G. psilostemon |
| G27 | G. × cantabrigiense ‘Biokovo’ | Robertium | Parent 1: G. maccrorhizum, Parent 2: G. dalmaticum |
| G30 | G. cinereum ‘Laurence Flatman’ | Erodioidea | G. cinereum |
| G35 | G. endressii | Geranium | G. endressii |
| G37 | G. endressii ‘Trevor Bath’ | Geranium | G. endressii |
| G38 | G. himalayense ‘Baby Blue’ | Geranium | G. himalayense |
| G39 | G. himalayense ‘Derrick Cook’ | Geranium | G. himalayense |
| G42 | G. macrorrhizum ‘Czakor’ | Robertium | G. maccrorhizum |
| G44 | G. macrorrhizum ‘White Ness’ | Robertium | G. maccrorhizum |
| G45 | G. maculatum ‘Album’ | Geranium | G. maculatum |
| G46 | G. maculatum ‘Elizabeth Ann’ | Geranium | G. maculatum |
| G49 | G. × oxonianum ‘Katherine Adele’ | Geranium | Parent 1: G. versicolor, Parent 2: G. endressi |
| G50 | G. × oxonianum ‘Southcombe Double’ | Geranium | Parent 1: G. versicolor, Parent 2: G. endressi |
| G54 | G. phaeum ‘Angelina’ | Erodioidea | G. phaeum |
| G57 | G. pratense ‘Algera Double’ | Geranium | G. pratense |
| G61 | G. pratense ‘Purple Ghost’ | Geranium | G. pratense |
| G62 | G. psilostemon | Geranium | G. psilostemon |
| G64 | G. renardii | Geranium | G. renardii |
| G69 | G. sanguineum ‘Album’ | Geranium | G. sanguineum |
| G71 | G. sylvaticum ‘Album’ | Geranium | G. sylvaticum |
| G73 | G. versicolor | Geranium | G. versicolor |
| G75 | G. ‘Bloomtime’ | Geranium | Parent 1: G. wallichianum, Parent 2: G. himalayense |
| G76 | G. wallichianum ‘Havana Blue’ | Geranium | G. wallichianum |
| G77 | G. wlassovianum | Geranium | G. wlassovianum |
| G80 | G. ‘Blushing Turtle’ | Geranium | G. sanguineum |
| Growing Season | 2020 | 2021 |
|---|---|---|
| Number of all crosses | 349 | 1155 |
| Number of combinations | 96 | 236 |
| Number of harvested seeds | 15 | 175 |
| Number of combinations that produced seeds | 5 | 36 |
| Number of combinations that produced healthy seedlings | 2 | 15 |
| Number of healthy seedlings | 3 | 33 |
| Average of cJaccard of crosses | 0.81 | 0.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akbarzadeh, M.; Quataert, P.; Van Huylenbroeck, J.; Werbrouck, S.P.O.; Dhooghe, E. Prediction Model for Breeding Hardy Geraniums. Horticulturae 2023, 9, 617. https://doi.org/10.3390/horticulturae9060617
Akbarzadeh M, Quataert P, Van Huylenbroeck J, Werbrouck SPO, Dhooghe E. Prediction Model for Breeding Hardy Geraniums. Horticulturae. 2023; 9(6):617. https://doi.org/10.3390/horticulturae9060617
Chicago/Turabian StyleAkbarzadeh, Mehrdad, Paul Quataert, Johan Van Huylenbroeck, Stefaan P. O. Werbrouck, and Emmy Dhooghe. 2023. "Prediction Model for Breeding Hardy Geraniums" Horticulturae 9, no. 6: 617. https://doi.org/10.3390/horticulturae9060617
APA StyleAkbarzadeh, M., Quataert, P., Van Huylenbroeck, J., Werbrouck, S. P. O., & Dhooghe, E. (2023). Prediction Model for Breeding Hardy Geraniums. Horticulturae, 9(6), 617. https://doi.org/10.3390/horticulturae9060617