Next Article in Journal
Unusual Compositions of Fe-Nb Alloy Precipitates in Iron-Implanted LiNbO3
Next Article in Special Issue
Driving a Molecular Spin-Peierls System into a Short Range Ordered State through Chemical Substitution
Previous Article in Journal
Superconducting Gap Structure of Filled Skutterudite LaOs4As12 Compound through μSR Investigations
Previous Article in Special Issue
A Simulation Independent Analysis of Single- and Multi-Component cw ESR Spectra
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Magnetochemistry
Volume 9
Issue 5
10.3390/magnetochemistry9050120
magnetochemistry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Communication

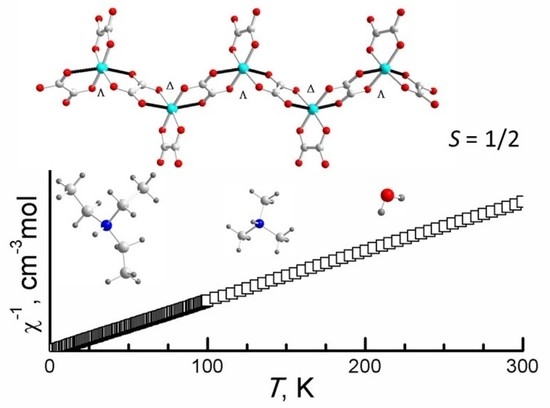
Two One-Dimensional Copper-Oxalate Frameworks with the Jahn–Teller Effect: [(CH3)3NH]2[Cu(μ-C2O4)(C2O4)]·2.5H2O (I) and [(C2H5)3NH]2[Cu(μ-C2O4)(C2O4)]·H2O (II)

by
Bin Zhang
1,*,
Yan Zhang
2,
Zheming Wang
3,*,
Yang Sun
4,
Tongling Liang
4,
Mei Liu
4 and
Daoben Zhu
1,*
1
Organic Solid Laboratory, BNLMS, CMS & Institute of Chemistry, Chinese Academy of Sciences, Beijing 100190, China
2
Department of Physics, Institute of Condensed Material Physics, Peking University, Beijing 100871, China
3
State Key Laboratory of Rare Earth Materials Chemistry and Applications, BNLMS, College of Chemistry and Molecular Engineering, Peking University, Beijing 100871, China
4
BNLMS, CMS & Institute of Chemistry, Chinese Academy of Sciences, Beijing 100190, China
*
Authors to whom correspondence should be addressed.
Magnetochemistry 2023, 9(5), 120; https://doi.org/10.3390/magnetochemistry9050120
Submission received: 20 March 2023 / Revised: 27 April 2023 / Accepted: 27 April 2023 / Published: 29 April 2023
(This article belongs to the Special Issue Functional Molecular Materials Insights—a Themed Issue in Honour of Professor Manuel Almeida on the Occasion of His 70th Birthday)
Browse Figures
Versions Notes

Abstract

:
Two one-dimensional oxalate-bridged Cu(II) ammonium salts, [(CH3)3NH]2[Cu(μ-C2O4)(C2O4)]·2.5H2O (I) and [(C2H5)3NH]2[Cu(μ-C2O4)(C2O4)]·H2O (II) were obtained and characterized. They were composed of ammonium: (CH3)3NH+ in (I), (C2H5)3NH+ in (II), [Cu(μ-C2O4)(C2O4)2−]n and H2O. The Jahn–Teller-distorted Cu(II) is octahedrally coordinated by six O atoms from three oxalates and forms a one-dimensional zigzag chain. The hydrogen bonds between ammonium, the anion and H2O form a three-dimensional network. There is no hydrogen bond between the anion chains. They were insulated at 20 °C with a relative humidity of 40%. Ferromagnetic and weak-ferromagnetic behaviors were observed in I and II, separately. No long-range ordering was observed above 2 K.

Graphical Abstract

1. Introduction

The Jahn–Teller effect plays an important role in inorganic superconductors and colossal magneto-resistance materials [1,2,3,4,5,6,7,8,9]. Interesting conductivity and magnetic behaviors are expected when the Jahn–Teller effect exists in molecular crystals, such as metal–organic frameworks. Oxalate (C2O42−), as one of the most commonly used short connectors, plays a key role in molecular-based magnets [10,11,12]. Long-range ordering has been reported in metal–oxalate framework compounds from one-dimensional zigzag chains (K2Fe(μ-C2O4)(C2O4), K2Co(μ-C2O4)(C2O4), Co(μ-C2O4)(μ-HOC3H6OH), TTF[Fe(μ-C2O4)Cl2] and κ-BETS2[Fe(μ-C2O4)Cl2]) to two-dimensional honeycomb lattices ([(C4H9)4N][CrMn(μ-C2O4)3], A[MIIFeIII(μ-C2O4)3] (A = ammonium; M = Mn, Fe), [C5H10N3O]2[Fe2(μ-C2O4)3], Fe2(μ-C2O4)3·4H2O) and square lattices ([Fe(μ-C2O4)(CH3OH)]n) to three-dimensional metal–oxalate framework compounds ([Co(bpy)3][Co2(μ-C2O4)3]ClO4, Mn(μ-C2O4)(H2O)0.25, [ZII(bpy)3][MIICrIII(μ-C2O4)3][ClO4] (M = Mn, Fe, Co, Ni) and (Me4N)6[Mn3Cr4(μ-C2O4)12]·6H2O), while a single chain magnet [C12H24O6K]0.5[(C12H24O6)(FC6H4NH3)]0.5[Co(H2O)2Cr(μ-C2O4)(C2O4)2] has been reported [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29].
Quantum spin liquid is an intriguing magnetic state, where spin ordering or freezing prevents spin frustration in a resonating valence bond (RVB) state. In 1979, P. W. Anderson proposed the RVB state in S = 1/2, a two-dimensional triangular lattice [30]. In 1987, he proposed that La2CuO4 is a parent compound of cuprate superconductors. The antiferromagnetic insulator La2CuO4 turns into a diamagnetic superconductor after hole doping, and a quantum spin liquid with Jahn–Teller distortion on Cu(II) is an indispensable magnetic state [31]. The spin-frustrated copper-oxalate framework with Jahn–Teller distortion supports a platform for molecular-based quantum spin liquids [32,33]. Strong antiferromagnetic interactions without a long-range ordering above 2 K with spin frustration were observed in two-dimensional honeycomb lattices: θ21-(BEDT-TTF)3[Cu2(μ-C2O4)3]·2CH3OH, θ21-(BETS-TTF)3[Cu2(μ-C2O4)3]·2CH3OH, [(C3H7)3NH]2[Cu2(μ-C2O4)3]·2.2H2O, hydrogen-bonded square lattice β″-(BEDT-TTF)3[Cu2(μ-C2O4)(C2O4)2(CH3OH)(H2O)], and three-dimensional hyperhoneycomb lattice [(C2H5)3NH]2[Cu2(μ-C2O4)3] [34,35,36,37,38]. [(C2H5)3NH]2[Cu2(μ-C2O4)3], which is a quantum spin liquid with no long-range ordering was observed until 60 mK [39]. In these compounds, the antiferromagnetic behavior depends on the antiferromagnetic interaction between the ferromagnetic couple. The magnetic structure of [(C2H5)3NH]2[Cu2(μ-C2O4)3] is lower than the three-dimensional, with the coexistence of ferromagnetic and antiferromagnetic interactions between Jahn–Teller distorted Cu(II) [37,39]. Researching the magnetic properties of Jahn–Teller distorted one-dimensional copper-oxalate frameworks [Cu(μ-C2O4)(C2O4)22−]n without the hydrogen bond between anions will help us to quantitatively analyze the magnetic interaction in Jahn–Teller-distorted two-dimensional and three-dimensional copper-oxalate frameworks and design new candidate quantum spin liquids. Two one-dimensional copper-oxalate framework compounds, [(CH3)3NH]2[Cu(μ-C2O4)(C2O4)]·2.5H2O (I) and [(C2H5)3NH]2[Cu(μ-C2O4)(C2O4)]·H2O (II), have been obtained and characterized. The related work is presented here.

2. Experiment

[(CH3)3NH]2[Cu(μ-C2O4)(C2O4)]·2.5H2O (I) and [(C2H5)3NH]2[Cu(μ-C2O4)(C2O4)]·H2O (II) were obtained from a methanol solution of Cu(NO3)2·3H2O and H2C2O4·2H2O with (CH3)3N for I and (C2H5)3N for II in a 1:3:5 ratio at room temperature. Bulk blue plateful crystals of I and II were obtained after four weeks. The crystal was washed with CH3COOC2H5 and dried. Elemental analysis calculated (%) for C10H25CuN2O10.50 (I): C 29.67, H 6.22 and N 6.92 and found C 29.87, H, 6.08 and N 6.97. For C16H34CuN2O9 (II): C 41.60, H 7.42, N 6.06 and found C 42.03, H 7.46 and N 6.11.
Elemental analyses of carbon, hydrogen and nitrogen were performed using the Flash EA 1112 elemental analyzer. The IR spectra were recorded on a Bio-rad FTS6000/UMA500 spectrometer (Figure S1). Thermogravimeter analysis was carried out on a Shimadzu DTG-60 analyzer at a 10 °C/min heating rate from room temperature to 550 °C under N2 gas with an Al bag. I remains stable until 40 °C, and II remains stable until 80 °C.
X-ray powder diffraction was carried out using a Rigaku RINT2000 diffractometer at room temperature with Cu Kα radiation (λ = 1.54056 Å) in a flat-plate geometry (Figures S2 and S3).
Single-crystal X-ray diffraction was carried out on an Enraf-Nonius KappaCCD diffractometer at room temperature. The crystal structure was solved using the direct method and refined using the full-matrix least square on F2 using the SHELX program, with anisotropic thermal parameters for all non-hydrogen atoms [40]. The hydrogen atoms on C and N were located through calculation, and on H2O they were located through a difference Fourier map. All of the H were refined isotropically. The crystallographic data are listed in Table S1.
The resistance measurement was performed on a single crystal at Tonghui TH2828. Gold wires were attached to the best developed surfaces of a single crystal with a size of 0.40 ∗ 0.30 ∗ 0.11 mm (I) and 0.71 ∗ 0.60 ∗ 0.17 mm (II) using gold paste. The two-probe conductivity was measured at 20 °C and a relative humidity (RH) of 40%.
Magnetization measurements were performed on a polycrystalline sample tightly packed into a capsule on a Quantum Design MPMS 7XL SQUID system above 2 K. Susceptibility data were corrected for the diamagnetism of the sample by Pascal constants and background by experimental measurement of the sample holder [41]. Temperature-dependent magnetization was performed under an applied field of 1000 G. Isothermal magnetization was measured at 2 K from 0 to 65 kG.

3. Result and Discussion

I crystallizes in a triclinic system with space group P 1. There are two (CH3)3NH+, one Cu2+, one oxalate anion, two half-oxalate anions and one-and-a-half H2O coexisting in an independent unit (Figure 1). Cu2+ is coordinated to two O atoms from one bidentate oxalate (O1 and O2) and four O atoms from two disbidentate oxalates in the Q3 Jahn–Teller distortion mode of a CuO6 octahedron [8].
The Cu–O distances are 1.954(2)~1.992(2) Å on the equatorial plane and 2.292(2) Å, 2.329(2) Å from the apex as a result of the Jahn–Teller distortion. The elongated Cu–O bonds (Cu1–O6, Cu1–O8) on the Jahn–Teller-distorted octahedron around Cu2+ are highlighted with solid black lines (Figure 2). The cis O–Cu–O angles are 77.73° and 77.12° for the bridged oxalate, 83.56° for the terminal oxalate, and 90.70°, 98.89°, 90.31°, 96.85°, 93.12° and 100.68° among the terminal and bridged oxalate. The trans O–Cu–O angles are in the range of 161.01(6)~171.46(6)°. The axial Cu to oxalate-oxygen angles are 109.17° (Cu1–O6–C3) and 108.27° (Cu1–O8–C4). A one-dimensional zigzag [Cu(μ-C2O4)(C2O4)2−]n is formed along the b axis.
The one-dimensional [Cu(μ-C2O4)(C2O4)2−]n zigzag chain running along the b axis is separated by (CH3)3NH+ (N1) along the c axis, and there are hydrogen bonds N–H⋯O, C–H⋯O between the cation and the out O atom in the oxalate. The anionic sheets composed of a [Cu(μ-C2O4)(C2O4)2−]n chain and (CH3)3NH+ in a 1:1 ratio are separated by a cation layer composed of a zigzag (CH3)3NH+ (N2) chain and a zigzag H2O chain along the c axis. There are hydrogen bonds between neighboring H2O molecules. Five H2O molecules formed a hydrogen-bond [H2O]5 linear cluster along the c axis (Figure 3).
At last, the hydrogen bonds N–H⋯O and C–H⋯O between the ammonium and the inner O of the terminal and bridged oxalate, the O–H⋯O between H2O and the oxalate, and the O–H⋯O between the H2O molecules form a three-dimensional hydrogen-bonded network in crystal (Figure 4). There is no hydrogen bond between the anions.
II crystallizes in a monoclinic system with the space group P21/c. There are two (C2H5)3NH+, one Cu2+, one and two half oxalates, and one H2O in an independent unit (Figure 5). The Cu2+ is octahedrally coordinated by six O atoms from two bisbidentate oxalates and one bidentate oxalate, as in I, with Cu–O distances of 1.960(2)~1.999(2) Å on the equatorial plane, and Cu1–O8: 2.314(2) Å and Cu1–O7: 2.368(2) Å from the apex. The Cu–O distances of II in the equatorial plane are shorter than the direction of the apex as a result of the Q3 Jahn–Teller distortion mode, as in I. The cis–O–Cu–O angles are 75.93° and 77.79° for the bridged oxalate, 88.31° for the terminal oxalate and 92.34°, 93.72°, 95.98°, 89.66°, 95.48° and 102.48° between the terminal and bridged oxalate. The trans-O–Cu–O angles are in the range of 160.21(7)~172.64(7)°. The axial Cu to oxalate-oxygen angles are 108.09° (Cu1–O1–C3) and 108.53° (Cu1–O8–C4). The Cu–O distances and O–Cu–O angles in I and II are in the same range of the Cu–oxalate coordination polymer [29,30,34,35,37,38]. A one-dimensional oxalate-bridged zigzag [Cu(μ-C2O4)(C2O4)2−]n chain is formed along the b axis.
The zigzag chain in I and II is centrosymmetric with the inversion center located at the middle point of the oxalate bridge; thus, the metal sites have a ΔΛΔΛ configuration along the b axis in I and II (Figure 6). It is similar to [(CH3)4N]2Cu(C2O4)2(H2O) [42,43]. The hydrogen bonds between ammonium and the anion and H2O and the anion influence the bond length of the CuO6 octahedron due to the Jahn–Teller distortion. Due to the magnetic orbitals of dx2 − y2 on Cu(II) with the unpaired electrons parallel to each other and the axial Cu to oxalate-oxygen angles, which are sensitive to magnetic interaction and smaller than 109.5°, a ferromagnetic interaction was expected [43,44].
In II, the [Cu(μ-C2O4)(C2O4)2−]n chain is surrounded by zigzag chains of (C2H5)3NH+ and H2O. A pair (C2H5)3NH+ column separates two zigzag chains along the c axis. There are hydrogen bonds between the N of the ammonium and the O on the bridged oxalate: N1–H1⋯O5 2.10 Å/146.9°, N1–H1⋯O8 2.44 Å/131.7°. There are hydrogen bonds between the N of the ammonium and the O on the terminal oxalate: N2–H2⋯O3 2.20 Å/139°, N2–H2⋯O4 2.21 Å/143.1°. There are hydrogen bonds between H2O and the terminal oxalate: O9–H4⋯O3 2.11 Å/159°, O9–H3⋯O4 2.20 Å/164°. There are hydrogen bonds between ammonium and H2O: C8–H8C⋯O1 2.45 Å/174°; C15–H15A⋯O8 2.40 Å/155°. The hydrogen bond forms a two-dimensional (2D) network on the (201) plane (Figure 7). There is no hydrogen bond between the one-dimensional [Cu(μ-C2O4)(C2O4)2−)]n chains.
On the basis of the hydrogen bonded cation layer, the resistance, as the proton conductivity under different relative humidities (RH), was measured. Depending on the thermal dynamic analysis, I and II dehydrate at 40 °C (I) and 76 °C (II), losing H2O, with a relative weight of 11.2% in I and 4% in II; therefore, the experiment should be carried out below 40 °C (Figure 8). When the RH increased, the conductivity of I and II increased. Under a relatively high RH, the surfaces of the crystal were covered with debris at first, which was solvable in gel. Although the sample was restored to a solid state when the RH decreased and reached the same value as the beginning, the sample turned out to be in a polycrystalline state but not a single crystal. When a single crystal of I or II was exposed to air under a low relative humidity, such as when the relative humidity was lower than 35%, guest molecules, such as H2O, in I and II would escape from the crystal, leading to crystalline collapse. The crystal surface remained transparent and clear after measurements at 20 °C and an RH of 40%. The resistance comes from the intrinsic behavior of the crystal. The resistance is 1 × 109 Ω·cm in I and 1 × 107 Ω·cm in II. They are insulators.
On the basis of the oxalate-bridging and Jahn–Teller distortion of the Cu(II) ion, Cu(II) in an independent unit, and the magnetic properties were studied per Cu2+/mol.
At 300 K, the χT value of I was 0.473 cm3 K mol−1 and g = 2.25. It is higher than 0.375 cm3 K mol−1 for an isolated, spin only Cu(II) ion with S = 1/2, g = 2.00 and in the range of Cu2+ compounds [34,35,36,37,45,46]. The χT value remained stable at 0.478 cm3 K mol−1 at 40 K and increased slowly, reaching 0.71 cm3 K mol−1 at 2 K. No bifurcation is observed from zero-field-cool magnetization and field-cooled magnetization (ZFCM/FCM) measurements from 2 K to 100 K under 100 G (Figure S4). The magnetic data were fitted with the Curie–Weiss law from 2 to 300 K: C = 0.4711(2) cm−1·K/mol, θ = 0.61(6) K and R = 1.37 × 10−5. It suggests a ferromagnetic interaction in I (Figure 9) [47,48].
A one-dimensional Baker–Rushbrooke–Gilbert model was used to fit the temperature-dependent magnetization above 2 K, yielding J = 0.60(2) cm−1, g = 2.31(1) and R = 9.2 × 10−4 (Figure 10) [49]. It shows an intrachain ferromagnetic interaction and corresponds with the Curie–Weiss fitting.
At 2 K, the isothermal magnetization (M) saturated at 1.11 Nβ (N is Avogadro’s number and β is the Bohn magneton, 1 Nβ = 5585 cm−1 G mol−1) at 65 kG (Figure 11). The average anisotropic g-factor calculated from isothermal magnetization at 2 K is 2.22. It is in the range of 2.25 from χT at 300 K and 2.31 from Baker–Rushbrooke–Gilbert model fitting.
In II, the χT value was 0.443 cm3 K mol−1 at 300 K with a g-factor of 2.13. It is higher than the 0.375 cm3 K mol−1 of an isolated, spin only Cu(II) ion with S = 1/2, g = 2.00. It is in the range of Cu2+ compounds, as in I [34,35,36,37,45,46]. As the temperature decreased, the χT value decreased slowly to 0.393 cm3 K mol−1 around 30 K, and then increased, reaching 0.446 cm3 K mol−1 at 2 K (Figure 12). No bifurcation was observed in the ZFCM/FCM measurement from 2 K to 100 K under 100 G (Figure S5). The magnetic data were fitted with Curie–Weiss law from 80 to 300 K with C = 0.462(1)) cm−1·K/mol, g = −14.2(4) K and R = 3.8 × 10−5 (Figure 12).
A one-dimensional Baker–Rushbrooke–Gilbert model combined with exchange coupling was used to fit the temperature-dependent magnetization from 2 to 300 K with J = 0.87(2) cm−1, g = 2.035(3), zJ = −0.65(2) cm−1 and R = 6.76 × 10−5 (Figure 13) [50]. It shows that intrachain ferromagnetic interaction is stronger than intrachain antiferromagnetic interaction. The g-factor is in the range of 2.13 from χT at 300 K.
At 2 K, the magnetization increases with increasing field and is saturated at 0.89 Nβ at 65 kG (Figure 14). The average anisotropic g-factor calculated from isothermal magnetization at 2 K is 1.78. Its magnetic behavior is not the same as expected. This means the Jahn–Teller effect is important to the magnetic property of the copper-oxalate framework. This is different from the compounds [CrMn(C2O4)3−]n, where in the ferromagnetic order, temperature and isothermal magnetization at 2 K are the same as those taken from ammonium salts to charge-transfer salts [19,51,52]. Depending on the difference in magnetic behaviors between I and II, the Jahn–Teller effect will help us to obtain molecular-based candidate quantum spin liquid and to look for a new superconductor and colossal magnetoresistance material from copper-oxalate frameworks as cuprate superconductors and colossal magnetoresistance material.

4. Conclusions

Two one-dimensional copper-oxalate framework compounds were obtained and characterized. The hydrogen bonds among ammonium, H2O and the copper-oxalate framework form a three-dimensional hydrogen-bond network, and there is no hydrogen bond between the one-dimensional [Cu(μ-C2O4)(C2O4)2−]n chains. The Q3-mode Jahn–Teller distortion of elongated CuO6 octahedrons is observed. They are insulators. The Jahn–Teller effect results the ferromagnetic and weak-ferromagnetic interaction between Cu(II) in I and II. No long-range ordering is observed above 2 K.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/magnetochemistry9050120/s1, Table S1. Crystallographic data of I and II; Figure S1. IR spectra on crystalline I (top) and II (bottom); Figure S2. Experimental X-ray powder diffraction pattern of crystalline sample and simulated one based on single crystal structure of I. I shows preferred orientation; Figure S3. Experimental X-ray powder diffraction pattern of crystalline sample and simulated one based on single crystal structure of II; Figure S4. ZFCM/FCM of polycrystal of I under 100 G; Figure S5. ZFCM/FCM of polycrystal of II under 100 G.

Author Contributions

The manuscript was written with the contributions of all authors. Funding acquisition: B.Z., D.Z. and Y.Z. Synthesized the sample: Y.Z. Performed the magnetic measurements: Z.W. Performed the single-crystal X-ray diffraction experiments: T.L., Y.S. and M.L. Performed the X-ray experiments and data analysis: B.Z. Conducted experiments: B.Z. and Z.W. Analyzed the data: B.Z., Y.Z. and Z.W. Wrote the main manuscript text. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China: 22273109, 22073106, 21573242 and 21173230 and the Strategic Priority Research Program (B) of the Chinese Academy of Sciences (Grant No. XDB12030100).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The IR spectra, powder X-ray diffraction pattern and ZFCM/FCM of I and II are available in the Supplementary Materials.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Jahn, H.A.; Teller, E. Stability of polyatomic molecules in degenerate electronic states-I—Orbital degeneracy. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1937, 161, 220–235. [Google Scholar]
  2. Opik, U.; Pryce, M.H.L. Studies of the Jahn-Teller effect. I. A survey of the static problem. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1957, 238, 425–427. [Google Scholar]
  3. Longuet-Higgins, H.C.; Opik, U.; Pryce, H.I.; Sack, R.A. Studies of the Jahn-Teller effect. II. The dynamical problem. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1958, 244, 1–16. [Google Scholar]
  4. Bednorz, J.G.; Muller, K.A. Possible high Tc superconductivity in the Ba−La−Cu−O system. Z. Für Phys. B Condens. Matter 1986, 64, 189–193. [Google Scholar] [CrossRef]
  5. Radaelli, P.G.; Cox, D.E.; Marezio, M.; Cheong, S.W.; Schiffer, P.E.; Ramirez, A.P. Simultaneous Structural, Magnetic, and Electronic Transitions in La 1−x Cax MnO3 with x= 0.25 and 0.50. Phys. Rev. Lett. 1995, 75, 4488–4491. [Google Scholar] [CrossRef]
  6. Dagotto, E.; Hotta, T.; Moreo, A. Colossal magnetoresistant materials: The key role of phase separation. Phys. Rep. 2001, 344, 1–153. [Google Scholar] [CrossRef]
  7. Dagotto, E. Complexity in strongly correlated electronic systems. Science 2005, 309, 257–262. [Google Scholar] [CrossRef] [PubMed]
  8. Goodenough, J.B. Jahn-Teller phenomena in solids. Annu. Rev. Mater. Sci. 1998, 28, 1–27. [Google Scholar] [CrossRef]
  9. Bersuker, I.B. The Jahn-Teller Effect; Cambridge University Press, Edinburgh Building: Cambridge, UK, 2006. [Google Scholar]
  10. Staub, U.; Scagnoli, V.; Muleders, A.M.; Janousch, M.; Honda, Z.; Tonnerre, J.M. Charge/orbital ordering vs. Jahn-Teller distortion in La0. 5Sr1. 5MnO4. Europhys. Lett. 2006, 76, 926–932. [Google Scholar] [CrossRef]
  11. Clement, R.; Decurtins, S.; Gruselle, M.; Train, C. Polyfunctional two-(2D) and three-(3D) dimensional oxalate bridged bimetallic magnets. Mon. Chem. 2003, 134, 117–135. [Google Scholar] [CrossRef]
  12. Daze, C.L.F.; Noa, M.A.; Nenwa, J.; Ohrstrom, L. Natural and synthetic metal oxalates–a topology approach. CrystEngComm 2019, 21, 6156–6164. [Google Scholar] [CrossRef]
  13. Hursthouse, M.B.; Light, M.E.; Price, D.J. One-Dimensional Magnetism in Anhydrous Iron and Cobalt Ternary Oxalates with Rare Trigonal-Prismatic Metal Coordination Environment. Angew. Chem. Int. Ed. 2004, 43, 472–475. [Google Scholar] [CrossRef]
  14. Zhang, B.; Zhang, Y.; Chang, G.; Wang, Z.; Zhu, D. Crystal-to-Crystal Transformation from K2 [Co (C2O4)2(H2O)2]·4H2O to K2 [Co (μ-C2O4)(C2O4)]. Magnetochemistry 2021, 7, 77. [Google Scholar] [CrossRef]
  15. Duan, Z.; Zhang, Y.; Zhang, B.; Zhu, D. Co(C2O4)(HO(CH2)3OH): An antiferromagnetic neutral zigzag chain compound showing long-range ordering of spin canting. Inorg. Chem. 2008, 47, 9152–9154. [Google Scholar] [CrossRef]
  16. Zhang, B.; Wang, Z.; Fujiwara, H.; Kabayashi, H.; Kurmoo, M.; Inoue, K.; Mori, T.; Gao, S.; Zhang, Y.; Zhu, D. Tetrathiafulvalene [FeIII (C2O4)Cl2]: An Organic–Inorganic Hybrid Exhibiting Canted Antiferromagnetism. Adv. Mater. 2005, 17, 1988–1991. [Google Scholar] [CrossRef]
  17. Zhang, B.; Wang, Z.; Zhang, Y.; Takahashi, K.; Okano, Y.; Cui, H.; Kobayashi, H.; Inoue, K.; Kurmoo, M.; Pratt, F.; et al. Hybrid Organic—Inorganic Conductor with a Magnetic Chain Anion: κ-BETS2 [FeIII(C2O4)Cl2][BETS = Bis (ethylenedithio) tetraselenafulvalene]. Inorg. Chem. 2006, 45, 3275–3280. [Google Scholar] [CrossRef]
  18. Tamaki, H.; Zhong, Z.J.; Matsumoto, N.; Kida, S.; Koikawa, M.; Achiwa, N.; Hashimoto, Y.; Okawa, H. Design of metal-complex magnets. Syntheses and magnetic properties of mixed-metal assemblies {NBu4[MCr (ox)3]}x (NBu4+ = tetra (n-butyl) ammonium ion; ox2− = oxalate ion; M = Mn2+, Fe2+, Co2+, Ni2+, Cu2+, Zn2+). J. Am. Chem. Soc. 1992, 114, 6974–6979. [Google Scholar] [CrossRef]
  19. Mathoniere, C.; Nuttall, C.J.; Carling, S.G.; Day, P. Ferrimagnetic mixed-valency and mixed-metal tris (oxalato) iron (III) compounds: Synthesis, structure, and magnetism. Inorg. Chem. 1996, 35, 1201–1206. [Google Scholar] [CrossRef] [PubMed]
  20. Duan, Z.; Zhang, Y.; Zhang, B.; Zhu, D. Two Homometallic Antiferromagnets Based on Oxalato-Bridged Honeycomb Assemblies:(A)2[MII(C2O4)3](A= Ammonium Salt Derived from Diethylenetriamine; MII= Fe2+, Co2+). Inorg. Chem. 2009, 48, 2140–2146. [Google Scholar] [CrossRef] [PubMed]
  21. Rousse, G.; Rodriguez-Carvajal, J. Oxalate-mediated long-range antiferromagnetism order in Fe2(C2O4)3 4H2O. Dalton Trans. 2016, 45, 14311–14316. [Google Scholar] [CrossRef] [PubMed]
  22. Zhang, B.; Zhang, Y.; Zhang, J.; Li, J.; Zhu, D. A neutral molecular-based layered magnet [Fe (C2O4)(CH3OH)]n exhibiting magnetic ordering at TN≈ 23 K. Dalton Trans. 2008, 5037–5040. [Google Scholar] [CrossRef] [PubMed]
  23. Decurtins, S.; Schmalle, H.W.; Schneuwly, P.; Esling, J.; Gutlich, P. A concept for the synthesis of 3-dimensional homo-and bimetallic oxalate-bridged networks [M2(ox)3]n. Structural, moessbauer, and magnetic studies in the field of molecular-based magnets. J. Am. Chem. Soc. 1994, 116, 9521–9528. [Google Scholar] [CrossRef]
  24. Hernandez-Molina, M.; Lloret, F.; Ruiz-Perez, C.; Julve, M. Weak Ferromagnetism in chiral 3-dimensional oxalato-bridged cobalt (II) compounds. Crystal structure of [Co(bpy)3][Co2(ox)3]ClO4. Inorg. Chem. 1998, 37, 4131–4135. [Google Scholar] [CrossRef]
  25. Coronado, E.; Galan-Mascaros, J.R.; Gomez-Garzia, C.J.; Martinez-Agudo, J.M. Molecule-based magnets formed by bimetallic three-dimensional oxalate networks and chiral tris (bipyridyl) complex cations. The series [ZII (bpy)3][ClO4][MIICrIII (ox)3](ZII= Ru, Fe, Co, and Ni; MII= Mn, Fe, Co, Ni, Cu, and Zn; ox= oxalate dianion). Inorg. Chem. 2001, 40, 113–120. [Google Scholar] [CrossRef]
  26. Zhang, B.; Zhang, Y.; Zhang, J.; Hao, X.; Zhu, D. Mn (C2O4)(H2O)0.25: An antiferromagnetic oxalato-based cage compound. Dalton Trans. 2011, 40, 5430–5432. [Google Scholar] [CrossRef] [PubMed]
  27. Mon, M.; Grancha, T.; Verdaguer, M.; Train, C.; Armentano, D.; Pardo, E. Solvent-Dependent Self-Assembly of an Oxalato-Based Three-Dimensional Magnet Exhibiting a Novel Architecture. Inorg. Chem. 2016, 55, 6845–6847. [Google Scholar] [CrossRef] [PubMed]
  28. Thorarinsdottir, A.E.; Harris, T.D. Metal–organic framework magnets. Chem. Rev. 2020, 120, 8716–8789. [Google Scholar] [CrossRef]
  29. Coronado, E.; Galan-Mascaros, J.R.; Marti-Gastaldo, C. Single chain magnets based on the oxalate ligand. J. Am. Chem. Soc. 2008, 130, 14987–14989. [Google Scholar] [CrossRef]
  30. Anderson, P.W. Resonating valence bonds: A new kind of insulator? Mater. Res. Bull. 1973, 8, 153–160. [Google Scholar] [CrossRef]
  31. Anderson, P.W. The resonating valence bond state in La2CuO4 and superconductivity. Science 1987, 235, 1196–1198. [Google Scholar] [CrossRef]
  32. Ramirez, A.P. Strongly geometrically frustrated magnets. Annu. Rev. Mater. Sci. 1994, 24, 453–480. [Google Scholar] [CrossRef]
  33. Balent, I. Spin liquids in frustrated magnets. Nature 2010, 464, 199–208. [Google Scholar] [CrossRef] [PubMed]
  34. Zhang, B.; Zhang, Y.; Zhu, D. (BEDT-TTF)3Cu2(C2O4)3(CH3OH)2: An organic–inorganic hybrid antiferromagnetic semiconductor. Chem. Commun. 2012, 48, 197–198. [Google Scholar] [CrossRef]
  35. Zhang, B.; Zhang, Y.; Wang, Z.; Gao, S.; Guo, Y.; Liu, F.; Zhu, D. BETS3[Cu2(C2O4)3](CH3OH)2: An organic–inorganic hybrid antiferromagnetic metal (BETS = bisethylene(tetraselenfulvalene)). CrystEngComm 2013, 15, 3529–3535. [Google Scholar] [CrossRef]
  36. Zhang, B.; Zhang, Y.; Wang, Z.; Wang, D.; Yang, D.; Gao, Z.; Chang, G.; Guo, Y.; Mori, T.; Zhao, Z.; et al. Organic–inorganic hybrid metallic conductors based on bis (ethylenedithio) tetrathiafulvalene cations and antiferromagnetic oxalate-bridged copper (ii) dinuclear anions. J. Mater. Chem. C 2022, 10, 2845–2852. [Google Scholar] [CrossRef]
  37. Zhang, B.; Zhang, Y.; Wang, Z.; Wang, D.; Baker, P.; Pratt, F.; Zhu, D. Candidate quantum spin liquid due to dimensional reduction of a two-dimensional honeycomb lattice. Sci. Rep. 2014, 4, 6451. [Google Scholar] [CrossRef]
  38. Zhang, B.; Zhang, Y.; Zhu, D. [(C2H5)3NH]2Cu2(C2O4)3: A three-dimensional metal–oxalato framework showing structurally related dielectric and magnetic transitions at around 165 K. Dalton Trans. 2012, 14, 8509–8511. [Google Scholar] [CrossRef] [PubMed]
  39. Zhang, B.; Baker, P.; Zhang, Y.; Wang, D.; Wang, Z.; Su, S.; Zhu, D.; Pratt, F.L. Quantum spin liquid from a three-dimensional copper-oxalate framework. J. Am. Chem. Soc. 2018, 140, 122–125. [Google Scholar] [CrossRef] [PubMed]
  40. Sheldrick, G.M. Shelx-97; University of Göttingen: Göttingen, Germany, 1997. [Google Scholar]
  41. Bain, A.B.; Berry, J.F. Diamagnetic corrections and Pascal’s constants. J. Chem. Educ. 2008, 85, 532–536. [Google Scholar] [CrossRef]
  42. Zhang, B. CCDC843075. Available online: http://www.ccdc.cam.ac.uk (accessed on 5 September 2011).
  43. Vilela, R.S.; Oliveira, T.I.; Martins, F.T.; Ellena, J.A.; Lloret, F.; Julve, M.; Cangussu, D. Synthesis, crystal structure and magnetic properties of the helical oxalate-bridged copper(II) chain {[(CH3)4N]2[Cu(C2O4)2]·H2O}n. Comptes Rendus Chim. 2012, 15, 856–865. [Google Scholar] [CrossRef]
  44. Cano, J.; Alemany, P.; Alvarez, M.; Verdaguer, M.; Ruiz, E. Exchange Coupling in Oxalato-Bridged Copper (ii) Binuclear Compounds: A Density Functional Study. Chem. A Eur. J. 1998, 4, 476–484. [Google Scholar] [CrossRef]
  45. Carlin, R.; van Duyneveldt, A. Magnetic Properties of Transition Metal Compounds; Springer: New York, NY, USA, 1977; p. 69. [Google Scholar]
  46. Zhang, B.; Zhang, Y.; Zhang, J.; Yan, X.; Zhu, D. Step by step crystal-to-crystal transformation from 1D K2Cu(C2O4)2(H2O)4 (1) to 1D K2Cu(C2O4)2(H2O)2 (2) and then 1D K2Cu(C2O4)2 (3) by dehydration. CrystEngComm 2016, 18, 5062–5065. [Google Scholar] [CrossRef]
  47. Kahn, O. Molecular Magnetism; VCH Publisher Inc.: New York, NY, USA, 1993; pp. 10–29. [Google Scholar]
  48. Mugiraneza, S.; Hallas, A.M. Tutorial: A beginner’s guide to interpreting magnetic susceptibility data with the Curie-Weiss law. Commun. Phys. 2022, 5, 95. [Google Scholar] [CrossRef]
  49. Baker, G.A.; Rushbrooke, G.S.; Gilbert, H.E. High-temperature series expansions for the spin-½ Heisenberg model by the method of irreducible representations of the symmetric group. Phys. Rev. 1964, 135, A1272–A1277. [Google Scholar] [CrossRef]
  50. Carling, R.L. Magnetochemistry; Springer: Berlin/Heidelberg, Germany, 1986; pp. 132–133. [Google Scholar]
  51. Coronado, E.; Galan-Mascaros, J.R.; Gomez-Gracia, C.J.; Laukhin, V. Coexistence of ferromagnetism and metallic conductivity in a molecule-based layered compound. Nature 2000, 408, 447–449. [Google Scholar] [CrossRef] [PubMed]
  52. Alberola, A.; Coronado, E.; Galan-Mascaros, J.R.; Gimenez-Saiz, C.; Gomez-Garcia, C.J. A molecular metal ferromagnet from the organic donor bis (ethylenedithio) tetraselenafulvalene and bimetallic oxalate complexes. J. Am. Chem. Soc. 2003, 125, 10774–10775. [Google Scholar] [CrossRef] [PubMed]
Magnetochemistry 09 00120 g001 550
Figure 1. Atomic structure of I in an independent unit with scheme label and 50% ellipsoids. Asymmetry code for C3A, O5A, O6A: 2 − x, 2 − y, −z; C4A, O7A, O8A: 1 − x, 1 − y, −z; H15A: −x, 2 − y, −z.
Figure 1. Atomic structure of I in an independent unit with scheme label and 50% ellipsoids. Asymmetry code for C3A, O5A, O6A: 2 − x, 2 − y, −z; C4A, O7A, O8A: 1 − x, 1 − y, −z; H15A: −x, 2 − y, −z.
Magnetochemistry 09 00120 g001
Magnetochemistry 09 00120 g002 550
Figure 2. The zigzag anionic chain in I.
Figure 2. The zigzag anionic chain in I.
Magnetochemistry 09 00120 g002
Magnetochemistry 09 00120 g003 550
Figure 3. Arrangement of (CH3)3NH+ and H2O in cation layer of I. Dashed yellow lines are hydrogen bonds between H2O in [H2O]5.
Figure 3. Arrangement of (CH3)3NH+ and H2O in cation layer of I. Dashed yellow lines are hydrogen bonds between H2O in [H2O]5.
Magnetochemistry 09 00120 g003
Magnetochemistry 09 00120 g004 550
Figure 4. Packing diagram of I viewed along the b axis. Dash yellow lines are hydrogen bonds. Color code: Cu, cyan; O, red; C, white; N, blue; H, light grey.
Figure 4. Packing diagram of I viewed along the b axis. Dash yellow lines are hydrogen bonds. Color code: Cu, cyan; O, red; C, white; N, blue; H, light grey.
Magnetochemistry 09 00120 g004
Magnetochemistry 09 00120 g005 550
Figure 5. ORTEP drawing of II in an independent unit with scheme label and 50% ellipsoids. Asymmetry code for C3A, O5, O7: −x, −y, 1 − z; C4A, C6A, C8A: −x, 1 − y, 1 − z.
Figure 5. ORTEP drawing of II in an independent unit with scheme label and 50% ellipsoids. Asymmetry code for C3A, O5, O7: −x, −y, 1 − z; C4A, C6A, C8A: −x, 1 − y, 1 − z.
Magnetochemistry 09 00120 g005
Magnetochemistry 09 00120 g006 550
Figure 6. The zigzag anionic chain in II.
Figure 6. The zigzag anionic chain in II.
Magnetochemistry 09 00120 g006
Magnetochemistry 09 00120 g007 550
Figure 7. Arrangement of (C2H5)3NH+, zigzag [Cu(μ-C2O4)(C2O4)2−]n chain and H2O on two-dimensional hydrogen-bond network viewed along the b axis in II. Dashed yellow lines are hydrogen bonds. Color code: Cu, cyan; O, red; C, white; N, blue; H, light grey.
Figure 7. Arrangement of (C2H5)3NH+, zigzag [Cu(μ-C2O4)(C2O4)2−]n chain and H2O on two-dimensional hydrogen-bond network viewed along the b axis in II. Dashed yellow lines are hydrogen bonds. Color code: Cu, cyan; O, red; C, white; N, blue; H, light grey.
Magnetochemistry 09 00120 g007
Magnetochemistry 09 00120 g008 550
Figure 8. Schematic TGA curves of I and II. Above 300 °C, the final residue is CuO.
Figure 8. Schematic TGA curves of I and II. Above 300 °C, the final residue is CuO.
Magnetochemistry 09 00120 g008
Magnetochemistry 09 00120 g009 550
Figure 9. χT vs. T (left, black empty square), 1/χ vs. T (right, black empty circle) and Curie–Weiss fitting data (red solid) of I.
Figure 9. χT vs. T (left, black empty square), 1/χ vs. T (right, black empty circle) and Curie–Weiss fitting data (red solid) of I.
Magnetochemistry 09 00120 g009
Magnetochemistry 09 00120 g010 550
Figure 10. Temperature-dependent susceptibility of I. Black empty square is experimental data. Red solid curve is the best fit from the Baker–Rushbrooke–Gilbert model.
Figure 10. Temperature-dependent susceptibility of I. Black empty square is experimental data. Red solid curve is the best fit from the Baker–Rushbrooke–Gilbert model.
Magnetochemistry 09 00120 g010
Magnetochemistry 09 00120 g011 550
Figure 11. Isothermal magnetization of I at 2 K.
Figure 11. Isothermal magnetization of I at 2 K.
Magnetochemistry 09 00120 g011
Magnetochemistry 09 00120 g012 550
Figure 12. cT vs. T (left, black empty square), 1/c vs. T (right, black empty circle) and Curie–Weiss fitting data (red solid) of II.
Figure 12. cT vs. T (left, black empty square), 1/c vs. T (right, black empty circle) and Curie–Weiss fitting data (red solid) of II.
Magnetochemistry 09 00120 g012
Magnetochemistry 09 00120 g013 550
Figure 13. Temperature-dependent susceptibility of II. Empty solid square, is experimental data. Red solid curve is best fit from the Baker–Rushbrooke–Gilbert model with exchange coupling.
Figure 13. Temperature-dependent susceptibility of II. Empty solid square, is experimental data. Red solid curve is best fit from the Baker–Rushbrooke–Gilbert model with exchange coupling.
Magnetochemistry 09 00120 g013
Magnetochemistry 09 00120 g014 550
Figure 14. Isothermal magnetization of II at 2 K.
Figure 14. Isothermal magnetization of II at 2 K.
Magnetochemistry 09 00120 g014
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Zhang, B.; Zhang, Y.; Wang, Z.; Sun, Y.; Liang, T.; Liu, M.; Zhu, D. Two One-Dimensional Copper-Oxalate Frameworks with the Jahn–Teller Effect: [(CH3)3NH]2[Cu(μ-C2O4)(C2O4)]·2.5H2O (I) and [(C2H5)3NH]2[Cu(μ-C2O4)(C2O4)]·H2O (II). Magnetochemistry 2023, 9, 120. https://doi.org/10.3390/magnetochemistry9050120

AMA Style

Zhang B, Zhang Y, Wang Z, Sun Y, Liang T, Liu M, Zhu D. Two One-Dimensional Copper-Oxalate Frameworks with the Jahn–Teller Effect: [(CH3)3NH]2[Cu(μ-C2O4)(C2O4)]·2.5H2O (I) and [(C2H5)3NH]2[Cu(μ-C2O4)(C2O4)]·H2O (II). Magnetochemistry. 2023; 9(5):120. https://doi.org/10.3390/magnetochemistry9050120

Chicago/Turabian Style

Zhang, Bin, Yan Zhang, Zheming Wang, Yang Sun, Tongling Liang, Mei Liu, and Daoben Zhu. 2023. "Two One-Dimensional Copper-Oxalate Frameworks with the Jahn–Teller Effect: [(CH3)3NH]2[Cu(μ-C2O4)(C2O4)]·2.5H2O (I) and [(C2H5)3NH]2[Cu(μ-C2O4)(C2O4)]·H2O (II)" Magnetochemistry 9, no. 5: 120. https://doi.org/10.3390/magnetochemistry9050120

APA Style

Zhang, B., Zhang, Y., Wang, Z., Sun, Y., Liang, T., Liu, M., & Zhu, D. (2023). Two One-Dimensional Copper-Oxalate Frameworks with the Jahn–Teller Effect: [(CH3)3NH]2[Cu(μ-C2O4)(C2O4)]·2.5H2O (I) and [(C2H5)3NH]2[Cu(μ-C2O4)(C2O4)]·H2O (II). Magnetochemistry, 9(5), 120. https://doi.org/10.3390/magnetochemistry9050120

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop