Reducing the Computational Cost for Artificial Intelligence-Based Battery State-of-Health Estimation in Charging Events
Abstract
:1. Introduction
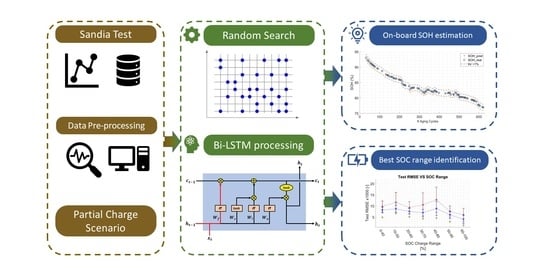
2. Materials and Methods
2.1. Data Preprocessing Phase
- Cycle index, number of charge–discharge cycle;
- Cell current [A];
- Cell voltage [V];
- Charge and discharge capacity [Ah];
- Charge and discharge energy [Wh];
- Cell temperature [°C];
- Environmental temperature [°C].
2.2. AI Neural Networks Learning Process
2.3. Model Performance Evaluation
- the RMSE considering the test dataset,
- the coefficient of determination , and
- the customized regression accuracy (CRA) coefficient, which compared the predicted SOH, , with the corresponding measured value, through an identified threshold .
2.4. Variable SOC Windows during Partial Charging Events
- 80%
- 60%
- 40%
- 20%.
2.5. Best Partial Charging Length and Optimal SOC Window Identification for SOH Estimation
3. Results and Discussion
3.1. Analysis #1: Variable SOC Windows for Partial Charging
3.2. Analysis #2: Computational Cost and Memory Occupancy for Best SOC Charging Window Length Identification
3.3. Analysis #3: Best SOC Window Identification for Optimal SOH Estimation
3.4. Best SOC Window: Training and Validation Information
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SOH | State-of-Health |
| BMS | Battery Management System |
| AI | Artificial Intelligence |
| SOC | State of Charge |
| Bi-LSTM | Bidirectional Long Short-term Memory |
| CCCV | Constant Current Constant Voltage |
| RMSE | Root Mean Squared Error |
| CV | Constant Voltage |
| EOL | End of Life |
| ECM | Equivalent Circuit Model |
| EIS | Electrochemical Impedance Spectroscopy |
| PSO | Particle Swarm Optimizer |
| FNN | Feed-Forward Neural Netwrk |
| CNN | Convolutional Neural Network |
| NMC | Nickel Manganese Cobalt |
| CRA | Customized Regression Accuracy |
| thr | Threshold |
| Optimal length | |
| SOC window | |
| Coefficient of determination | |
| CPU | Central Processing Unit |
References
- Van den Bossche, A. Light and Ultralight electric vehicles. In 4ième Conférence Internationale sur le Génie Electrique (CIGE 2010) (No. 2, pp. 3–9); Université de Bechar Algérie: Béchar, Algeria, 2010. [Google Scholar]
- Blomgren, G.E. The Development and Future of Lithium Ion Batteries. J. Electrochem. Soc. 2016, 164, A5019. [Google Scholar] [CrossRef] [Green Version]
- Keshan, H.; Thornburg, J.; Ustun, T.S. Comparison of lead-acid and lithium ion batteries for stationary storage in off-grid energy systems. In Proceedings of the 2016 4th IET Clean Energy and Technology Conference, Kuala Lumpur, Malaysia, 14–15 November 2019. [Google Scholar]
- Vutetakis, D.; Timmons, J. A Comparison of Lithium-Ion and Lead-Acid Aircraft Batteries. SAE Tech. Paper 2008, 1, 2875. [Google Scholar]
- See, K.W.; Wang, G.; Zhang, Y.; Wang, Y.; Meng, L.; Gu, X.; Zhang, N.; Lim, K.C.; Zhao, L.; Xie, B. Critical review and functional safety of a battery management system for large-scale lithium-ion battery pack technologies. Int. J. Coal. Sci. Technol. 2022, 9, 36. [Google Scholar] [CrossRef]
- Feng, X.; Ouyang, M.; Liu, X.; Lu, L.; Xia, Y.; He, X. Thermal runaway mechanism of lithium ion battery for electric vehicles: A review. Energy Storage Mater. 2017, 10, 246–267. [Google Scholar] [CrossRef]
- Tran, M.K.; Mevawalla, A.; Aziz, A.; Panchal, S.; Xie, Y.; Fowler, M. A Review of Lithium-Ion Battery Thermal Runaway Modeling and Diagnosis Approaches. Processes 2022, 10, 1192. [Google Scholar] [CrossRef]
- Leng, F.; Tan, C.; Pecht, M. Effect of Temperature on the Aging rate of Li Ion Battery Operating above Room Temperature. Sci. Rep. 2015, 5, 12967. [Google Scholar] [CrossRef] [Green Version]
- Ma, S.; Jiang, M.; Tao, P.; Song, C.; Wu, J.; Wang, J.; Deng, T.; Shang, W. Temperature effect and thermal impact in lithium-ion batteries: A review. Prog. Nat. Sci. Mater. Int. 2018, 28, 6. [Google Scholar] [CrossRef]
- Jaydeep, B. Effect of Temperature on Battery Life and Performance in Electric Vehicle. Int. J. Sci. Res. 2012, 2, 1–3. [Google Scholar]
- Ouyang, D.; He, Y.; Weng, J.; Liu, J.; Chen, M.; Wang, J. Influence of low temperature conditions on lithium-ion batteries and the application of an insulation material. RSC Adv. 2019, 9, 9053–9066. [Google Scholar] [CrossRef] [Green Version]
- Hossein, M.; Jason, H. Effects of overdischarge on performance and thermal stability of a Li-ion cell. J. Power Sources 2006, 160, 1395–1402. [Google Scholar]
- Xu, B.; Oudalov, A.; Ulbig, A.; Andersson, G.; Kirschen, D.s. Modeling of Lithium-Ion Battery Degradation for Cell Life Assessment. IEEE Trans. Smart Grid 2016, 99, 1. [Google Scholar] [CrossRef]
- Raj, T.; Wang, A.A.; Monroe, C.W.; Howey, D.A. Investigation of Path-Dependent Degradation in Lithium-Ion Batteries. Eur. Chem. Soc. Publ. 2020, 3, 12. [Google Scholar] [CrossRef]
- Barcellona, S.; Colnago, S.; Dotelli, G.; Latorrata, S.; Piegari, L. Aging effect on the variation of Li-ion battery resistance as function of temperature and state of charge. J. Energy Storage 2022, 50, 104658. [Google Scholar] [CrossRef]
- Shahjalal, M.; Roy, P.K.; Shams, T.; Fly, A.; Chowdhury, J.I.; Ahmed, R.; Liu, K. A review on second-life of Li-ion batteries: Prospects, challenges, and issues. Energy 2022, 241, 122881. [Google Scholar] [CrossRef]
- Shu, X.; Shen, S.; Shen, J.; Zhang, Y.; Li, G.; Chen, Z.; Liu, Y. State of health prediction of lithium-ion batteries based on machine learning: Advances and perspectives. iScience 2021, 24, 11. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.; Tang, A.; Wang, W. A Review of SOH Estimation Methods in Lithium-ion Batteries for Electric Vehicle Applications. Energy Procedia 2015, 75, 1920–1925. [Google Scholar] [CrossRef] [Green Version]
- Berecibar, M.; Gandiaga, I.; Villarreal, I.; Omar, N.; Van Mierlo, J.; Van den Bossche, P. Critical review of state of health estimation methods of Li-ion batteries for real applications. Renew. Sustain. Energy Rev. 2016, 56, 572–587. [Google Scholar] [CrossRef]
- Noura, N.; Boulon, L.; Jemeï, S. A Review of Battery State of Health Estimation Methods: Hybrid Electric Vehicle Challenges. World Electr. Veh. J. 2020, 11, 66. [Google Scholar] [CrossRef]
- Han, H.; Xu, H.; Yuan, Z.; Shen, Y. A new SOH prediction model for lithium-ion battery for electric vehicles. In Proceedings of the 2014 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22–25 October 2014. [Google Scholar]
- Anselma, P.G.; Kollmeyer, P.; Lempert, J.; Zhao, Z.; Belingardi, G.; Emadi, A. Battery state-of-health sensitive energy management of hybrid electric vehicles: Lifetime prediction and ageing experimental validation. Appl. Energy 2021, 285, 116440. [Google Scholar] [CrossRef]
- Falai, A.; Giuliacci, T.A.; Misul, D.; Paolieri, G.; Anselma, P.G. Modeling and On-Road Testing of an Electric Two-Wheeler towards Range Prediction and BMS Integration. Energies 2022, 15, 2431. [Google Scholar] [CrossRef]
- Amir, S.; Gulzar, M.; Tarar, M.O.; Naqvi, I.H.; Zaffar, N.A.; Pecht, M.G. Dynamic Equivalent Circuit Model to Estimate State-of-Health of Lithium-Ion Batteries. IEEE Access 2022, 10, 18279–18288. [Google Scholar] [CrossRef]
- Galeotti, M.; Cinà, L.; Giammanco, C.; Cordiner, S.; Di Carlo, A. Performance analysis and SOH (state of health) evaluation of lithium polymer batteries through electrochemical impedance spectroscopy. Energy 2015, 89, 678–686. [Google Scholar] [CrossRef]
- Kieran, M.; Hemtej, G.; Kevin, M.R.; Tadhg, K. Review—Use of impedance spectroscopy for the estimation of Li-ion battery state of charge, state of health and internal temperature. J. Electrochem. Soc. 2021, 168, 080517. [Google Scholar]
- Sihvo, J.; Roinila, T.; Stroe, D.I. SOH analysis of Li-ion battery based on ECM parameters and broadband impedance measurements. In Proceedings of the IECON 2020 the 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020. [Google Scholar]
- Preetpal, S.; Che, C.; Cher, T.; Shyh-Chin, H. Semi-Empirical Capacity Fading Model for SoH Estimation of Li-Ion Batteries. Appl. Sci. 2019, 9, 3012. [Google Scholar]
- Huanyang, H.; Jinhao, M.; Yuhong, W.; Lei, C.; Jichang, P.; Ji, W.; Qian, X.; Tianqi, L.; Remus, T. An Enhanced Data-Driven Model for Lithium-Ion Battery State-of-Health Estimation with Optimized Features and Prior Knowledge. Automot. Innov. 2022, 5, 134–145. [Google Scholar] [CrossRef]
- Huang, J.; Wang, S.; Xu, W.; Shi, W.; Fernandez, C. A Novel Autoregressive Rainflow—Integrated Moving Average Modeling Method for the Accurate State of Health Prediction of Lithium-Ion Batteries. Processes 2021, 9, 795. [Google Scholar] [CrossRef]
- Gao, K.; Xu, J.; Li, Z.; Cai, Z.; Jiang, D.; Zeng, A. A Novel Remaining Useful Life Prediction Method for Capacity Diving Lithium-Ion Batteries. ACS Omega 2022, 7, 26701–26714. [Google Scholar] [CrossRef]
- Pang, B.; Chen, L.; Dong, Z. Data-Driven Degradation Modeling and SOH Prediction of Li-Ion Batteries. Energies 2022, 15, 5580. [Google Scholar] [CrossRef]
- Azis, N.A.; Joelianto, E.; Widyotriatmo, A. State of Charge (SoC) and State of Health (SoH) Estimation of Lithium-Ion Battery Using Dual Extended Kalman Filter Based on Polynomial Battery Model. In Proceedings of the 2019 6th International Conference on Instrumentation, Control, and Automation (ICA), Bandung, Indonesia, 31 July–2 August 2019. [Google Scholar]
- Li, R.; Li, W.; Zhang, H.; Zhou, Y.; Tian, W. On-Line Estimation Method of Lithium-Ion Battery Health Status Based on PSO-SVM. Front. Energy Res. 2021, 9, 401. [Google Scholar] [CrossRef]
- Bian, Z.; Ma, Y. An Improved Particle Filter Method to Estimate State of Health of Lithium-Ion Battery. IFAC-PapersOnLine 2021, 54, 344–349. [Google Scholar] [CrossRef]
- Chinedu, O.; Nagarajan, R. Statistical Characterization of the State-of-Health of Lithium-Ion Batteries with Weibull Distribution Function—A Consideration of Random Effect Model in Charge Capacity Decay Estimation. Batteries 2012, 3, 32. [Google Scholar]
- Sui, X.; He, S.; Vilsen, S.B.; Meng, J.; Teodorescu, R.; Stroe, D. A review of non-probabilistic machine learning-based state of health estimation techniques for Lithium-ion battery. Appl. Energy 2021, 300, 117346. [Google Scholar] [CrossRef]
- Bao, Z.; Jiang, J.; Zhu, C.; Gao, M. A New Hybrid Neural Network Method for State-of-Health Estimation of Lithium-Ion Battery. Energies 2022, 15, 4399. [Google Scholar] [CrossRef]
- Zhou, J.; He, Z.; Gao, M.; Liu, Y. Battery state of health estimation using the generalized regression neural network. In Proceedings of the 2015 8th International Congress on Image and Signal Processing (CISP), Shenyang, China, 14–16 October 2015. [Google Scholar]
- Jiantao, Q.; Feng, L.; Yuxiang, M.; Jiaming, F. A Neural-Network-based Method for RUL Prediction and SOH Monitoring of Lithium-Ion Battery. IEEE Access 2019, 1, 1. [Google Scholar]
- Fan, Y.; Wu, H.; Chen, W.; Jiang, Z.; Huang, X.; Chen, S.-Z. A Data Augmentation Method to Optimize Neural Networks for Predicting SOH of Lithium Batteries. In Proceedings of the International Conference on Robotics Automation and Intelligent Control (ICRAIC 2021), Wuhan, China, 26–28 November 2021. [Google Scholar]
- Jo, S.; Jung, S.; Roh, T. Battery State-of-Health Estimation Using Machine Learning and Preprocessing with Relative State-of-Charge. Energies 2021, 14, 7206. [Google Scholar] [CrossRef]
- Morello, R.; Di Rienzo, R.; Roncella, R.; Saletti, R.; Schwarz, R.; Lorentz, V.R.; Hoedemaekers, E.R.G.; Rosca, B.; Baronti, F. Advances in Li-Ion Battery Management for Electric Vehicles. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018. [Google Scholar]
- Gabbar, H.A.; Othman, A.M.; Abdussami, M.R. Review of Battery Management Systems (BMS) Development and Industrial Standards. Technologies 2021, 9, 28. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, Z.; Cao, R.; Wang, M.; Cheng, H.; Zhang, L.; Jiang, Y.; Li, Y.; Chen, B.; Ling, H.; et al. Implementation for a cloud battery management system based on the CHAIN framework. Energy AI 2021, 5, 100088. [Google Scholar] [CrossRef]
- Park, K.; Choi, Y.; Choi, W.J.; Ryu, H.-Y.; Kim, H. LSTM-Based Battery Remaining Useful Life Prediction With Multi-Channel Charging Profiles. IEEE Access 2020, 8, 20786–20798. [Google Scholar] [CrossRef]
- Cinomona, B.; Chung, C.; Tsai, M.-C. Long Short-Term Memory Approach to Estimate Battery Remaining Useful Life Using Partial Data. IEEE Access 2020, 8, 165419–165431. [Google Scholar] [CrossRef]
- Gong, D.; Gao, Y.; Kou, Y.; Wang, Y. State of health estimation for lithium-ion battery based on energy features. Energy 2022, 257, 124812. [Google Scholar] [CrossRef]
- Sun, S.; Sun, J.; Wang, Z.; Zhou, Z.; Cai, W. Prediction of Battery SOH by CNN-Bi-LSTM Network Fused with Attention Mechanism. Energies 2022, 15, 4428. [Google Scholar] [CrossRef]
- Pham, T.; Truong, L.; Nguyen, M.; Garg, A.; Gao, L.; Quan, T. Sequence-in-Sequence Learning for SOH Estimation of Lithium-Ion Battery. In Proceedings of the 11th International Conference on Electronics, Communications and Networks (CECNet), Xiamen, China, 18–21 November 2021. [Google Scholar]
- Dos Reis, G.; Strange, C.; Yadavc, M.; Li, S. Lithium-ion battery data and where to find it. Energy&AI 2021, 5, 100081. [Google Scholar]
- Sandia National Lab. Data for Degradation of Commercial Lithium-Ion Cells as a Function of Chemistry and Cycling Conditions. 2020. Available online: https://www.batteryarchive.org/snl_study.html (accessed on 10 June 2022).
- Medium. A Comparison of Grid Search and Randomized Search Using Scikit Learn. 2019. Available online: https://medium.com/@peterworcester_29377/a-comparison-of-grid-search-and-randomized-search-using-scikit-learn-29823179bc85 (accessed on 8 July 2022).
- Khan, N.; Ullah, F.U.M.; Ullah, A.; Lee, M.Y.; Baik, S.W. Batteries State of Health Estimation via Efficient Neural Networks With Multiple Channel Charging Profiles. IEEE Access 2020, 9, 7797–7813. [Google Scholar] [CrossRef]
- Siami-Namini, S.S.; Tavakoli, N.T.; Siami Namin, A.S.N. The Performance of LSTM and Bi-LSTM in Forecasting Time Series. In Proceedings of the IEEE International Conference on Big Data, Los Angeles, CA, USA, 9–12 December 2019. [Google Scholar]
- Machine Learning Mastery. Hyperparameter Optimization with Random Search and Grid Search. 2020. Available online: https://machinelearningmastery.com/hyperparameter-optimization-with-random-search-and-grid-search/ (accessed on 15 August 2022).
- Mathworks. Deep Learning with Time Series and Sequence Data. Available online: https://www.mathworks.com/help/deeplearning/deep-learning-with-time-series-sequences-and-text.html (accessed on 15 August 2022).
- Machine Learning Mastery. A Gentle Introduction to Dropout for Regularizing Deep Neural Networks. 2018. Available online: https://machinelearningmastery.com/dropout-for-regularizing-deep-neural-networks/ (accessed on 15 August 2022).
- Sebastian Ruder. An Overview of Gradient Descent Optimization Algorithms. 2016. Available online: https://ruder.io/optimizing-gradient-descent/ (accessed on 15 August 2022).
- Machine Learning Mastery. A Gentle Introduction to Early Stopping to Avoid Overtraining Neural Networks. 2018. Available online: https://machinelearningmastery.com/early-stopping-to-avoid-overtraining-neural-network-models/ (accessed on 20 August 2022).
- Machine Learning Mastery. Train-Test Split for Evaluating Machine Learning Algorithms. 2020. Available online: https://machinelearningmastery.com/train-test-split-for-evaluating-machine-learning-algorithms/ (accessed on 20 August 2022).
- Shi, M.; Xu, J.; Lin, C.; Mei, X. A fast state-of-health estimation method using single linear feature for lithium-ion batteries. Energy 2022, 256, 124652. [Google Scholar] [CrossRef]
- Bin, X.; Bing, X.; Luoshi, L. State of Health Estimation for Lithium-Ion Batteries Based on the Constant Current–Constant Voltage Charging Curve. Electronics 2020, 9, 1279. [Google Scholar]
- Ruan, H.; He, H.; Wei, Z.; Quan, Z.; Li, Y. State of Health Estimation of Lithium-ion Battery Based on Constant-Voltage Charging Reconstruction. IEEE J. Emerg. Sel. Top. Power Electron. 2021. [Google Scholar] [CrossRef]














| Cell Type | Cathode | Anode | Capacity (Ah) | Test Equipment |
|---|---|---|---|---|
| 18,650 NMC | NMC | graphite | 3.00 | High-precision Arbin |
| Charge C Rate | Discharge Crate | SOC Range | Environmental Temperature (°C) | N° Cycles |
|---|---|---|---|---|
| 0.50 | 2.00 | 0–100 | 25 | 661 |
| Data Length [% of SOC] | 100 | 80 | 60 | 40 | 20 |
|---|---|---|---|---|---|
| m | 2.67 | 5.82 | 9.92 | 8.81 | 3.68 |
| q | 0.97 | 0.93 | 0.88 | 0.89 | 0.96 |
| Test RMSE × 1000 | 5.65 | 8.04 | 7.33 | 6.80 | 8.93 |
| Test | 0.99 | 0.97 | 0.96 | 0.96 | 0.96 |
| Data Length [% of SOC] | 100 | 80 | 60 | 40 | 20 |
|---|---|---|---|---|---|
| Hidden Layers | 1 | 1 | 1 | 1 | 1 |
| Hidden Neurons | 59 | 30 | 29 | 47 | 52 |
| State Activation Function | tanh | tanh | tanh | tanh | softsign |
| DropOut | 0.2 | 0.3 | 0.2 | 0.1 | 0.1 |
| Batch Size | 128 | 32 | 64 | 32 | 64 |
| Learning Rate | 0.0090 | 0.0089 | 0.0060 | 0.0069 | 0.0044 |
| Optimization Algorithm | sgdm | sgdm | adam | sgdm | adam |
| Training Epochs | 190 | 84 | 108 | 264 | 186 |
| Charge Segment SOC [%] | 0–40 | 10–50 | 20–60 | 30–70 | 40–80 | 50–90 | 60–100 |
|---|---|---|---|---|---|---|---|
| m | 0.96 | 0.90 | 0.96 | 1.02 | 0.98 | 0.98 | 0.99 |
| q | 3.29 | 7.99 | 3.82 | −1.59 | 1.34 | 1.35 | 0.30 |
| Test RMSE | 5.45 | 7.52 | 5.23 | 4.09 | 4.81 | 3.12 | 1.27 |
| Test | 0.98 | 0.95 | 0.98 | 0.99 | 0.98 | 0.99 | 0.99 |
| Charge Segment SOC [%] | 0–40 | 10–50 | 20–60 | 30–70 | 40–80 | 50–90 | 60–100 |
|---|---|---|---|---|---|---|---|
| Hidden Layers | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Hidden Neurons | 15 | 15 | 65 | 54 | 42 | 51 | 51 |
| State Activation Function | tanh | tanh | softsign | softsign | tanh | softsign | softsign |
| DropOut | 0.3 | 0.3 | 0.3 | 0.2 | 0.5 | 0.5 | 0.5 |
| Batch Size | 16 | 16 | 32 | 64 | 64 | 32 | 32 |
| Learning Rate | 0.0098 | 0.0098 | 0.0055 | 0.0099 | 0.0086 | 0.0083 | 0.0083 |
| Optimization Algorithm | sgdm | sgdm | rmsprop | sgdm | sgdm | sgdm | sgdm |
| Training Epochs | 92 | 30 | 43 | 155 | 103 | 91 | 62 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Falai, A.; Giuliacci, T.A.; Misul, D.A.; Anselma, P.G. Reducing the Computational Cost for Artificial Intelligence-Based Battery State-of-Health Estimation in Charging Events. Batteries 2022, 8, 209. https://doi.org/10.3390/batteries8110209
Falai A, Giuliacci TA, Misul DA, Anselma PG. Reducing the Computational Cost for Artificial Intelligence-Based Battery State-of-Health Estimation in Charging Events. Batteries. 2022; 8(11):209. https://doi.org/10.3390/batteries8110209
Chicago/Turabian StyleFalai, Alessandro, Tiziano Alberto Giuliacci, Daniela Anna Misul, and Pier Giuseppe Anselma. 2022. "Reducing the Computational Cost for Artificial Intelligence-Based Battery State-of-Health Estimation in Charging Events" Batteries 8, no. 11: 209. https://doi.org/10.3390/batteries8110209
APA StyleFalai, A., Giuliacci, T. A., Misul, D. A., & Anselma, P. G. (2022). Reducing the Computational Cost for Artificial Intelligence-Based Battery State-of-Health Estimation in Charging Events. Batteries, 8(11), 209. https://doi.org/10.3390/batteries8110209