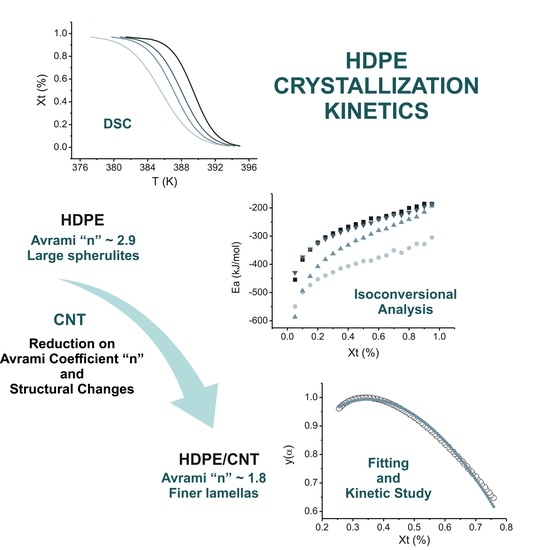
Non-Isothermal Crystallization Kinetic of Polyethylene/Carbon Nanotubes Nanocomposites Using an Isoconversional Method
Abstract
:1. Introduction
2. Theoretical Background
3. Materials and Methods
3.1. Materials
3.2. Nanocomposite Preparation
3.3. Differential Scanning Calorimeter (DSC)
3.4. Polarized Optical Microscopy (POM)
4. Results
4.1. Isoconversional Analysis of DSC Crystallization Data
4.2. Polarized Optical Microscopy (POM)
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Geyer, R.; Jambeck, J.R.; Law, K.L. Production, use, and fate of all plastics ever made. Sci. Adv. 2017, 3, 1–5. [Google Scholar] [CrossRef]
- Dordinejad, A.K.; Sharif, F.; Ebrahimi, M.; Rashedi, R. Rheological and Thermorheological Assessment of Polyethylene in Multiple Extrusion Process. Thermochim. Acta 2018, 668, 19–27. [Google Scholar] [CrossRef]
- Peacock, A. Handbook of Polyethylene: Structures: Properties, and Applications; CRC Press: New York, NY, USA, 2000. [Google Scholar]
- Roumeli, E.; Pavlidou, E.; Bikiaris, D.; Chrissafis, K. Microscopic observation and micromechanical modeling to predict the enhanced mechanical properties of multi-walled carbon nanotubes reinforced crosslinked high density polyethylene. Carbon 2014, 67, 475–487. [Google Scholar] [CrossRef]
- Mahfuz, H.; Adnan, A.; Rangari, V.K.; Jeelani, S. Manufacturing and characterization of carbon nanotube/polyethylene composites. Int. J. Nanosci. 2005, 4, 55–72. [Google Scholar] [CrossRef]
- Monthioux, M.; Kuznetsov, V.L. Who should be given the credit for the discovery of carbon nanotubes? Carbon 2006, 44, 1621–1623. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56. [Google Scholar] [CrossRef]
- De Volder, M.F.; Tawfick, S.H.; Baughman, R.H.; Hart, A.J. Carbon nanotubes: Present and future commercial applications. Science 2013, 339, 535–539. [Google Scholar] [CrossRef] [PubMed]
- Pop, E.; Mann, D.; Wang, Q.; Goodson, K.; Dai, H. Thermal conductance of an individual single-wall carbon nanotube above room temperature. Nano Lett. 2006, 6, 96–100. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Pham-Huy, L.A.; Dramou, P.; Xiao, D.; Zuo, P.; Pham-Huy, C. Carbon nanotubes: Applications in pharmacy and medicine. BioMed Res. Int. 2013, 2013, 578290. [Google Scholar] [CrossRef] [PubMed]
- Xie, X.-L.; Mai, Y.-W.; Zhou, X.-P. Dispersion and alignment of carbon nanotubes in polymer matrix: A review. Mater. Sci. Eng. R 2005, 49, 89–112. [Google Scholar] [CrossRef]
- Liu, X.-C.; Choi, J.-W. Improved dispersion of carbon nanotubes in polymers at high concentrations. Nanomaterials (Basel) 2002, 2, 329–347. [Google Scholar] [CrossRef]
- Kim, J.; Hong, S.M.; Kwak, S.; Seo, Y. Physical properties of nanocomposites prepared by in situ polymerization of high-density polyethylene on multiwalled carbon nanotubes. Phys. Chem. Chem. Phys. 2009, 11, 10851–10859. [Google Scholar] [CrossRef]
- Bekyarova, E.; Ni, Y.; Malarkey, E.B.; Montana, V.; McWilliams, J.L.; Haddon, R.C.; Parpura, V. Applications of carbon nanotubes in biotechnology and biomedicine. J. Biomed. Nanotechnol. 2005, 1, 3–17. [Google Scholar] [CrossRef]
- De Menezes, B.R.C.; Rodrigues, K.F.; Fonseca, B.C.S.; Ribas, R.G.; Montanheiro, T.L.A.; Thim, G.P. Recent advances in the use of carbon nanotubes as smart biomaterials. J. Mater. Chem. B 2019. [Google Scholar] [CrossRef]
- Carrión, F.J.; Espejo, C.; Sanes, J.; Bermúdez, M.D. Single-walled carbon nanotubes modified by ionic liquids as antiwear additives of thermoplastics. Compos. Sci. Technol. 2010, 70, 2160–2167. [Google Scholar] [CrossRef]
- De Menezes, B.R.C.; Ferreira, F.V.; Silva, B.C.; Simonetti, E.A.N.; Bastos, T.M.; Cividanes, L.S.; Thim, G.P. Effects of octadecylamine functionalization of carbon nanotubes on dispersion, polarity, and mechanical properties of CNT/HDPE nanocomposites. J. Mater. Sci. 2018, 53, 14311–14327. [Google Scholar] [CrossRef]
- Grady, B.P. Effects of carbon nanotubes on polymer physics. J. Polym. Sci. B Polym. Phys. 2012, 50, 591–623. [Google Scholar] [CrossRef] [Green Version]
- Vaughan, A.S.; Hosier, I.L. The effect of dibenzylidene sorbitol on the crystallization behaviour of polyethylene. J. Mater. Sci. 2008, 43, 2922–2928. [Google Scholar] [CrossRef]
- Zhang, C.; Yi, X.-S.; Asai, S.; Sumita, M. Morphology, crystallization and melting behaviors of isotactic polypropylene/high density polyethylene blend: Effect of the addition of short carbon fiber. J. Mater. Sci. 2000, 35, 673–683. [Google Scholar] [CrossRef]
- Tarani, E.; Wurm, A.; Schick, C.; Bikiaris, D.N.; Chrissafis, K.; Vourlias, G. Effect of graphene nanoplatelets diameter on non-isothermal crystallization kinetics and melting behavior of high density polyethylene nanocomposites. Thermochim. Acta 2016, 643, 94–103. [Google Scholar] [CrossRef]
- Shehzad, F.; Thomas, S.P.; Al-Harthi, M.A. Non-isothermal crystallization kinetics of high density polyethylene/graphene nanocomposites prepared by in-situ polymerization. Thermochim. Acta 2014, 589, 226–234. [Google Scholar] [CrossRef]
- Sahoo, R.K.; Panda, B.P.; Nayak, S.K.; Mohanty, S. Mechanical and morphological investigation of virgin polyethylene and silver nanoparticle-loaded nanocomposites film: Comprehensive analysis of kinetic models for non-isothermal crystallization. Bull. Mater. Sci. 2017, 40, 307–320. [Google Scholar] [CrossRef]
- Fan, Y.; Lou, J.; Jamali, J.; Lu, Y.; Wood, J. Effect of Clay Dispersion on the Nonisothermal and Isothermal Crystallization Behaviors of Polyethylene Composites. Polym. Plast. Technol. Eng. 2017, 56, 1646–1656. [Google Scholar] [CrossRef]
- Khawam, A.; Flanagan, D.R. Complementary Use of Model-Free and Modelistic Methods in the Analysis of Solid-State Kinetics. J. Phys. Chem. B 2005, 109, 10073–10080. [Google Scholar] [CrossRef] [PubMed]
- Khawam, A.; Flanagan, D.R. Role of isoconversional methods in varying activation energies of solid-state kinetics: II. Nonisothermal kinetic studies. Thermochim. Acta 2005, 436, 101–112. [Google Scholar] [CrossRef]
- Vyazovkin, S. Advanced isoconversional method. J. Therm. Anal. 1997, 49, 1493–1499. [Google Scholar] [CrossRef]
- Cividanes, L.S.; Brunelli, D.D.; Bertran, C.A.; Campos, T.M.B.; Thim, G.P. Urea effect on the mechanism of mullite crystallization. J. Mater. Sci. 2011, 46, 7384–7392. [Google Scholar] [CrossRef]
- Sharp, J.H.; Brindley, G.W.; Achar, B.N.N. Numerical Data for Some Commonly Used Solid State Reaction Equations. J. Am. Ceram. Soc. 1996, 49, 379–382. [Google Scholar] [CrossRef]
- Criado, J.M.; Málek, J.; Gotor, F.J. The applicability of the Šesták-Berggren kinetic equation in constant rate thermal analysis (CRTA). Thermochim. Acta 1990, 158, 205–213. [Google Scholar] [CrossRef]
- Málek, J.; Mitsuhashi, T. Testing Method for the Johnson–Mehl–Avrami Equation in Kinetic Analysis of Crystallization Processes. J. Am. Ceram. Soc. 2004, 83, 2103–2105. [Google Scholar] [CrossRef]
- Koga, N.; Malek, J. Accommodation of the actual solid-state process in the kinetic model function. Part 2. Applicability of the empirical kinetic model function to diffusion-controlled reactions, Thermochim. Acta 1996, 282–283, 69–80. [Google Scholar] [CrossRef]
- Málek, J.; Sesták, J.; Rouquerol, F.; Rouquerol, J.; Criado, J.M.; Ortega, A. Possibilities of two non-isothermal procedures (temperature- or rate-controlled) for kinetical studies. J. Therm. Anal. 1992, 38, 71–87. [Google Scholar] [CrossRef]
- Janković, B.; Adnađević, B.; Jovanović, J. Application of model-fitting and model-free kinetics to the study of non-isothermal dehydration of equilibrium swollen poly (acrylic acid) hydrogel: Thermogravimetric analysis. Thermochim. Acta 2007, 452, 106–115. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Wight, C.A. Kinetics in solids. Annu. Rev. Phys. Chem. 1997, 48, 125–149. [Google Scholar] [CrossRef] [PubMed]
- Azimi, H.R.; Rezaei, M.; Abbasi, F.; Charchi, A.; Bahluli, Y. Non-isothermal degradation kinetics of MMA-St copolymer and EPS lost foams. Thermochim. Acta 2008, 474, 72–77. [Google Scholar] [CrossRef]
- Laidler, K.J. The development of the Arrhenius equation. J. Chem. Educ. 1984, 61, 494. [Google Scholar] [CrossRef]
- Doyle, C.D. Estimating isothermal life from thermogravimetric data. J. Appl. Polym. Sci. 1962, 6, 639–642. [Google Scholar] [CrossRef]
- Zeman, S. Kinetic compensation effect and thermolysis mechanisms of organic polynitroso and polynitro compounds. Thermochim. Acta 1997, 290, 199–217. [Google Scholar] [CrossRef]
- Erceg, M.; Kovačić, T.; Perinović, S. Kinetic analysis of the non-isothermal degradation of poly(3-hydroxybutyrate) nanocomposites. Thermochim. Acta 2008, 476, 44–50. [Google Scholar] [CrossRef]
- López-Fonseca, R.; Landa, I.; Gutiérrez-Ortiz, M.A.; González-Velasco, J.R. Non-isothermal analysis of the kinetics of the combustion of carbonaceous materials. J. Therm. Anal. Calorim. 2005, 80, 65–69. [Google Scholar] [CrossRef]
- Ozawa, T. A New Method of Analyzing Thermogravimetric Data. Bull. Chem. Soc. Jpn. 1965, 38, 1881–1886. [Google Scholar] [CrossRef] [Green Version]
- Ozawa, T. Non-isothermal kinetics and generalized time. Thermochim. Acta 1986, 100, 109–118. [Google Scholar] [CrossRef]
- Gotor, F.J.; Criado, J.M.; Malek, J.; Koga, N. Kinetic Analysis of Solid-State Reactions: The Universality of Master Plots for Analyzing Isothermal and Nonisothermal Experiments. J. Phys. Chem. A 2000, 104, 10777–10782. [Google Scholar] [CrossRef]
- Koga, N. Kinetic analysis of thermoanalytical data by extrapolating to infinite temperature. Thermochim. Acta 1995, 258, 145–159. [Google Scholar] [CrossRef]
- Antunes, E.F.; Almeida, E.C.; Rosa, C.B.; de Medeiros, L.I.; Pardini, L.C.; Massi, M.; Corat, E.J. Thermal annealing and electrochemical purification of multi-walled carbon nanotubes produced by camphor/ferrocene mixtures. J. Nanosci. Nanotechnol. 2010, 10, 1296–1303. [Google Scholar] [CrossRef] [PubMed]
- Manchado, M.A.L.; Valentini, L.; Biagiotti, J.; Kenny, J.M. Thermal and mechanical properties of single-walled carbon nanotubes–polypropylene composites prepared by melt processing. Carbon 2005, 43, 1499–1505. [Google Scholar] [CrossRef]
- Ferreira, F.V.; Franceschi, W.; Menezes, B.R.C.; Brito, F.S.; Lozano, K.; Coutinho, A.R.; Cividanes, L.S.; Thim, G.P. Dodecylamine functionalization of carbon nanotubes to improve dispersion, thermal and mechanical properties of polyethylene based nanocomposites. Appl. Surf. Sci. 2017, 410, 267–277. [Google Scholar] [CrossRef]
- Cheng, J.; Pu, H.; Du, J. A processing method with high efficiency for low density polyethylene nanofibers reinforced by aligned carbon nanotubes via nanolayer coextrusion. Polymer 2017, 111, 222–228. [Google Scholar] [CrossRef]
- Kim, J.; Kwak, S.; Hong, S.M.; Lee, J.R.; Takahara, A.; Seo, Y. Nonisothermal Crystallization Behaviors of Nanocomposites Prepared by In Situ Polymerization of High-Density Polyethylene on Multiwalled Carbon Nanotubes. Macromolecules 2010, 43, 10545–10553. [Google Scholar] [CrossRef]
- Bakshi, S.R.; Tercero, J.E.; Agarwal, A. Synthesis and characterization of multiwalled carbon nanotube reinforced ultra high molecular weight polyethylene composite by electrostatic spraying technique. Compos. Part A Appl. Sci. Manuf. 2007, 38, 2493–2499. [Google Scholar] [CrossRef]
- Ferreira, C.I.; Dal Castel, C.; Oviedo, M.A.S.; Mauler, R.S. Isothermal and non-isothermal crystallization kinetics of polypropylene/exfoliated graphite nanocomposites. Thermochim. Acta 2013, 553, 40–48. [Google Scholar] [CrossRef]
- Seo, Y.; Kim, J.; Kim, K.U.; Kim, Y.C. Study of the crystallization behaviors of polypropylene and maleic anhydride grafted polypropylene. Polymer 2000, 41, 2639–2646. [Google Scholar] [CrossRef]
- Venkatesh, M.; Ravi, P.; Tewari, S.P. Isoconversional Kinetic Analysis of Decomposition of Nitroimidazoles: Friedman method vs Flynn–Wall–Ozawa Method. J. Phys. Chem. A 2013, 117, 10162–10169. [Google Scholar] [CrossRef] [PubMed]
- Ou, R.; Guo, C.; Xie, Y.; Wang, Q. Non-isothermal crystallization kinetics of kevlar fiber-reinforced wood flour/HDPE composites. BioResources 2011, 6, 4547–4565. [Google Scholar]
- Mandelkern, L. Crystallization of Polymers: Kinetics and Mechanisms, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004; pp. 11–27. [Google Scholar]
- Odian, G. Principles of Polymerization, 4th ed.; John Wiley & Sons: New York, NY, USA, 2004; pp. 301–302, 696–697. [Google Scholar]
- Zou, P.; Tang, S.; Fu, Z.; Xiong, H. Isothermal and non-isothermal crystallization kinetics of modified rape straw flour/high-density polyethylene composites. Int. J. Therm. Sci. 2009, 48, 837–846. [Google Scholar] [CrossRef]
- Hartley, F.; Lord, F.; Morgan, L. Crystallization phenomena in polymers—Effect of melt conditions and the temperature of crystallization on the course of the crystallization in polyethylene terephthalate. Philos. Trans. R. Soc. A 1954, 247, 23–34. [Google Scholar] [CrossRef]
- Banks, W.; Gordon, M.; Sharples, A. The crystallization of polyethylene after partial melting. Polymer 1963, 4, 289–302. [Google Scholar] [CrossRef]








| Model | Mechanism | f(α) |
|---|---|---|
| Šesták and Berggren (SB) [30] | Autocatalytic, General mechanism | |
| Johnson-Mehl-Avrami (JMA) [31] | Nucleation and growth | |
| Reaction Order (RO) [32,33] | One-parameter model | |
| Polany-Winger (R1) [34,35,36] | Phase boundary-controlled reaction (one-dimensional) | |
| Contracting cylinder (R2) [32,35] | Phase boundary-controlled reaction (contracting area) | |
| Contracting sphere (R3) [34,35] | Phase boundary-controlled reaction (contracting volume) | |
| Parabolic Law (D1) [36] | Diffusion (one-dimensional) | |
| Valenci (D2) [36] | Diffusion (two-dimensional) | |
| Jander (D3) [36] | Diffusion (three-dimensional) | |
| Brounshtein-Ginstling (D4) [36] | Diffusion (four-dimensional) |
| Sample | β (°C/min) | Ton (°C) | Tp (°C) | Xc (%) |
|---|---|---|---|---|
| HDPE Pure | 5 | 119 | 117 | 65 |
| 7 | 119 | 117 | 64 | |
| 10 | 118 | 116 | 66 | |
| 15 | 117 | 115 | 65 | |
| HDPE/ | 5 | 122 | 120 | 62 |
| CNT–P | 7 | 122 | 119 | 61 |
| 10 | 121 | 118 | 66 | |
| 15 | 121 | 116 | 65 | |
| HDPE/ | 5 | 122 | 119 | 65 |
| CNT–COOH | 7 | 121 | 118 | 63 |
| 10 | 121 | 117 | 66 | |
| 15 | 120 | 116 | 64 | |
| HDPE/ | 5 | 122 | 119 | 64 |
| CNT–ODA | 7 | 121 | 119 | 64 |
| 10 | 120 | 117 | 64 | |
| 15 | 120 | 116 | 63 |
| Sample | n |
|---|---|
| HDPE Pure | 2.9 |
| HDPE/CNT–P | 1.9 |
| HDPE/CNT–COOH | 1.8 |
| HDPE/CNT–ODA | 1.8 |
| n | Growth Type | Geometry |
|---|---|---|
| 5 ≤ n ≤ 6 | 3 dimensions | Sheaf-like |
| 3 ≤ n ≤ 4 | 3 dimensions | Spherulites |
| 2 ≤ n ≤ 3 | 2 dimensions | Lamellas |
| 1 ≤ n ≤ 2 | 1 dimension | Fibers |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Menezes, B.R.C.d.; Campos, T.M.B.; Montanheiro, T.L.d.A.; Ribas, R.G.; Cividanes, L.d.S.; Thim, G.P. Non-Isothermal Crystallization Kinetic of Polyethylene/Carbon Nanotubes Nanocomposites Using an Isoconversional Method. J. Compos. Sci. 2019, 3, 21. https://doi.org/10.3390/jcs3010021
Menezes BRCd, Campos TMB, Montanheiro TLdA, Ribas RG, Cividanes LdS, Thim GP. Non-Isothermal Crystallization Kinetic of Polyethylene/Carbon Nanotubes Nanocomposites Using an Isoconversional Method. Journal of Composites Science. 2019; 3(1):21. https://doi.org/10.3390/jcs3010021
Chicago/Turabian StyleMenezes, Beatriz Rossi Canuto de, Tiago Moreira Bastos Campos, Thais Larissa do Amaral Montanheiro, Renata Guimarães Ribas, Luciana de Simone Cividanes, and Gilmar Patrocínio Thim. 2019. "Non-Isothermal Crystallization Kinetic of Polyethylene/Carbon Nanotubes Nanocomposites Using an Isoconversional Method" Journal of Composites Science 3, no. 1: 21. https://doi.org/10.3390/jcs3010021
APA StyleMenezes, B. R. C. d., Campos, T. M. B., Montanheiro, T. L. d. A., Ribas, R. G., Cividanes, L. d. S., & Thim, G. P. (2019). Non-Isothermal Crystallization Kinetic of Polyethylene/Carbon Nanotubes Nanocomposites Using an Isoconversional Method. Journal of Composites Science, 3(1), 21. https://doi.org/10.3390/jcs3010021