Improving the Size Distribution of Polymeric Oblates Fabricated by the Emulsion-in-Gel Deformation Method
Abstract
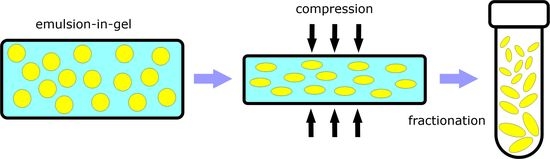
:1. Introduction
2. Materials and Methods
2.1. Emulsion Preparation
2.2. Emulsion-in-Gel Preparation
2.3. Gel Deformation and Droplet Solidification
2.4. Characterization
2.5. Fractionation
3. Results and Discussion
3.1. Emulsion-in-Gel Preparation
3.2. Emulsion-in-Gel Droplet Deformation
3.3. Particle Fractionation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Whitesides, G.M.; Grzybowski, B. Self-assembly at all scales. Science 2002, 295, 2418–2421. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Iyer, A.S.; Paul, K. Self-assembly: A review of scope and applications. IET Nanobiotechnol. 2015, 9, 122–135. [Google Scholar] [CrossRef] [PubMed]
- Vogel, N.; Retsch, M.; Fustin, C.-A.; del Campo, A.; Jonas, U. Advances in colloidal assembly: The design of structure and hierarchy in two and three dimensions. Chem. Rev. 2015, 115, 6265–6311. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Bu, X.; Yip, S.; Liang, X.; Ho, J.C. Self-assembly of colloidal particles for fabrication of structural color materials toward advanced intelligent systems. Adv. Intell. Syst. 2020, 2, 1900085. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Fan, Q.; Yin, Y. Colloidal self-assembly approaches to smart nanostructured materials. Chem. Rev. 2022, 122, 4976–5067. [Google Scholar] [CrossRef]
- Poon, W.C.K.; Pusey, P.N. Phase transition of spherical colloids. In Observation, Prediction, and Simulation of Phase Transitions in Complex Fluids; Baus, M., Rull, L.F., Ryckaert, J.-P., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1995. [Google Scholar]
- Poon, W.C.K. Colloidal Suspensions; Clarendon Press: Oxford, UK, 2012. [Google Scholar]
- Zaccarelli, E. Colloidal gels: Equilibrium and non-equilibrium routes. J. Phys. Condens. Matter 2007, 19, 323101. [Google Scholar] [CrossRef] [Green Version]
- Pusey, P.N.; Zaccarelli, E.; Valeriani, C.; Sanz, E.; Poon, W.C.K.; Cates, M.E. Hard spheres: Crystallization and glass formation. Phil. Trans. R. Soc. A 2009, 367, 4993–5011. [Google Scholar] [CrossRef] [Green Version]
- Lu, P.J.; Weitz, D.A. Colloidal particles: Crystals, glasses, and gels. Annu. Rev. Condens. Matter Phys. 2013, 4, 217–233. [Google Scholar]
- Lopez-Godoy, S.; Díaz-Leyva, P.; Kozina, A. Self-assembly in binary mixtures of spherical colloids. Adv. Coll. Inter. Sci. 2022, 308, 102748. [Google Scholar] [CrossRef]
- Sacanna, S.; Pine, D.J. Shape-anisotropic colloids: Building blocks for complex assemblies. Curr. Opin. Coll. Inter. Sci. 2011, 16, 96–105. [Google Scholar] [CrossRef]
- Dugyala, V.R.; Daware, S.V.; Basavaraj, G.M. Shape anisotropic colloids: Synthesis, packing behavior, evaporation driven assembly, and their application in emulsion stabilization. Soft Matter 2013, 9, 6711. [Google Scholar] [CrossRef]
- Lee, K.J.; Yoon, J.; Lahann, J. Recent advances with anisotropic particles. Curr. Opin. Coll. Inter. Sci. 2011, 16, 195–202. [Google Scholar] [CrossRef]
- Li, T.; Lilja, K.; Morris, R.J.; Brandani, G.B. Langmuir–Blodgett technique for anisotropic colloids: Young investigator perspective. J. Coll. Inter. Sci. 2019, 540, 420–438. [Google Scholar] [CrossRef]
- Krishnamurthy, S.; Kalapurakal, R.A.M.; Mani, E. Computer simulations of self-assembly of anisotropic colloids. J. Phys. Condens. Matter 2022, 34, 273001. [Google Scholar] [CrossRef]
- Furst, E.M. Directed self-assembly. Soft Matter 2013, 9, 9039–9045. [Google Scholar] [CrossRef]
- Yang, S.-M.; Kim, S.-H.; Lima, J.-M.; Yi, G.-R. Synthesis and assembly of structured colloidal particles. J. Mater. Chem. 2008, 18, 2177–2190. [Google Scholar] [CrossRef]
- Cuetos, A.; Martínez-Haya, B. Columnar phases of discotic spherocylinders. J. Chem. Phys. 2008, 129, 214706. [Google Scholar] [CrossRef]
- Fejer, S.N.; Chakrabarti, D.; Wales, D.J. Self-assembly of anisotropic particles. Soft Matter 2011, 7, 3553–3564. [Google Scholar] [CrossRef]
- Kao, P.-K.; Solomon, M.J.; Ganesan, M. Microstructure and elasticity of dilute gels of colloidal discoids. Soft Matter 2022, 18, 1350–1363. [Google Scholar] [CrossRef]
- Lu, J.; Bu, X.; Zhang, X.; Liu, B. Self-assembly of shape-tunable oblate colloidal particles into orientationally ordered crystals, glassy crystals and plastic crystals. Soft Matter 2021, 17, 6486–6494. [Google Scholar] [CrossRef]
- Hsiao, L.C.; Schultz, B.A.; Glaser, J.; Engel, M.; Szakasits, M.E.; Glotzer, S.C.; Solomon, M.J. Metastable orientational order of colloidal discoids. Nat. Commun. 2015, 6, 8507. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Doshia, N.; Zahr, A.S.; Bhaskar, S.; Lahann, J.; Mitragotri, S. Red blood cell-mimicking synthetic biomaterial particles. Proc. Natl. Acad. Sci. USA 2009, 106, 21495–21499. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Clay, N.; Kong, H. Non-spherical particles for targeted drug delivery. Chem. Eng. Sci. 2015, 125, 20–24. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kapate, N.; Clegg, J.R.; Mitragotri, S. Non-spherical micro- and nanoparticles for drug delivery: Progress over 15 years. Adv. Drug Delivery Rev. 2021, 177, 113807. [Google Scholar] [CrossRef]
- de Folter, J.W.J.; Hutter, E.M.; Castillo, S.I.R.; Klop, K.E.; Philipse, A.P.; Kegel, W.K. Particle shape anisotropy in Pickering emulsions: Cubes and peanuts. Langmuir 2014, 30, 955–964. [Google Scholar] [CrossRef]
- Ding, T.; Liu, Z.-F.; Song, K.; Clays, K.; Tung, C.-H. Photonic crystals of oblate spheroids by blown film extrusion of prefabricated colloidal crystals. Langmuir 2009, 25, 10218–10222. [Google Scholar] [CrossRef]
- Cho, Y.-S.; Kim, Y.K.; Chung, K.C.; Choi, C.J. Deformation of colloidal crystals for photonic band gap tuning. J. Dispers. Sci. Technol. 2011, 32, 1408–1415. [Google Scholar] [CrossRef]
- Florea, D.; Wyss, H.M. Towards the self-assembly of anisotropic colloids: Monodisperse oblate ellipsoids. J. Coll. Int. Sci. 2014, 416, 30–37. [Google Scholar] [CrossRef]
- Ahn, S.J.; Ahn, K.H.; Lee, S.J. Film squeezing process for generating oblate spheroidal particles with high yield and uniform sizes. Colloid Polym. Sci. 2016, 294, 859–867. [Google Scholar] [CrossRef]
- Courbaron, A.-C.; Cayre, O.J.; Paunov, V.N. A novel gel deformation technique for fabrication of ellipsoidal and discoidal polymeric microparticles. Chem. Commun. 2007, 2007, 628–630. [Google Scholar] [CrossRef]
- Mathaes, R.; Winter, G.; Besheer, A.; Engert, J. Non-spherical micro- and nanoparticles: Fabrication, characterization and drug delivery applications. Expert Opin. Drug Deliv. 2015, 12, 481–492. [Google Scholar] [CrossRef] [PubMed]
- Doshi, N.; Prabhakarpandian, B.; Rea-Ramsey, A.; Pant, K.; Sundaram, S.; Mitragotri, S. Flow and adhesion of drug carriers in blood vessels depend on their shape: A study using model synthetic microvascular networks. J. Control. Rel. 2010, 146, 196–200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yoo, J.-W.; Doshi, N.; Mitragotri, S. Endocytosis and intracellular distribution of PLGA particles in endothelial cells: Effect of particle geometry. Macromol. Rapid Commun. 2010, 31, 142–148. [Google Scholar] [CrossRef] [PubMed]
- Bibette, J. Depletion interactions and fractionated crystallization for polydisperse emulsion purification. J. Coll. Int. Sci. 1991, 147, 474–478. [Google Scholar] [CrossRef]
- Moroi, Y.; Motomura, K.; Matuura, R. The critical micelle concentration of sodium dodecyl sulfate-bivalent metal dodecyl sulfate mixtures in aqueous solutions. J. Coll. Int. Sci. 1974, 46, 111–117. [Google Scholar] [CrossRef]
- Peters, D. Ultrasound in materials chemistry. J. Mater. Chem. 1996, 6, 1605–1618. [Google Scholar] [CrossRef]
- Pratap-Singh, A.; Guo, Y.; Ochoa, S.L.; Fathordoobady, F.; Singh, A. Optimal ultrasonication process time remains constant for a specific nanoemulsion size reduction system. Sci. Rep. 2021, 11, 9241. [Google Scholar] [CrossRef]
- Gupta, A.; Eral, H.B.; Hatton, T.A.; Doyle, P.S. Controlling and predicting droplet size of nanoemulsions: Scaling relations with experimental validation. Soft Matter 2016, 12, 1452–1458. [Google Scholar] [CrossRef] [Green Version]
- Belgheisi, S.; Motamedzadegan, A.; Milani, J.M.; Rashidi, L.; Rafe, A. Impact of ultrasound processing parameters on physical characteristics of lycopene emulsion. J. Food Sci. Technol. 2021, 58, 484–493. [Google Scholar] [CrossRef]







| Sample | Surfactant | R, nm | |
|---|---|---|---|
| E1 | SDS | 710 | 0.32 |
| E2 | SDS | 750 | 0.26 |
| E3 | SDS | 550 | 0.27 |
| E4 | SDS | 710 | 0.35 |
| E5 | PVA | 720 | 0.14 |
| E6 | PVA | 610 | 0.20 |
| E7 | PVA | 850 | 0.22 |
| E8 | PVA | 620 | 0.19 |
| Sample | Surfactant | R, nm | R, nm | ||
|---|---|---|---|---|---|
| EGD1 | SDS | 710 | 0.32 | 990 | 0.53 |
| EGD2 | SDS | 750 | 0.26 | 930 | 0.46 |
| EGD4 | SDS | 710 | 0.35 | 1030 | 0.41 |
| EGD5 | PVA | 720 | 0.14 | 1100 | 0.37 |
| EGD6 | PVA | 610 | 0.20 | 900 | 0.40 |
| EGD7 | PVA | 850 | 0.22 | 960 | 0.35 |
| EGD8 | PVA | 620 | 0.19 | 750 | 0.38 |
| Sample | CMC | R, nm | |
|---|---|---|---|
| EGD5 | 0 | 1100 | 0.37 |
| EGD5F1 | 1 | 1130 | 0.24 |
| EGD5F2 | 2 | 1100 | 0.21 |
| EGD5F3 | 3 | 950 | 0.14 |
| EGD5F4 | 4 | 650 | 0.23 |
| EGD5F5 | 5 | 980 | 0.23 |
| Sample | Sucrose, % wt | R, nm | |
|---|---|---|---|
| EGD5 | 0 | 1100 | 0.37 |
| EGD5F1 | 20 | 515 | 0.25 |
| EGD5F2 | 25 | 780 | 0.34 |
| EGD5F3 | 30 | 740 | 0.33 |
| EGD5F4 | 35 | 730 | 0.30 |
| EGD5F5 | 40 | 24,000 | 0.36 |
| Sample | g-Force, g | R, nm | |
|---|---|---|---|
| EGD5 | 0 | 1100 | 0.37 |
| EGD5F1 | 1115 (5 min) | 490 | 0.14 |
| EGD5F2 | 1115 (1 min) | 1450 | 0.19 |
| EGD5F3 | 865 (1 min) | 2740 | 0.28 |
| EGD5F4 | 70 (1 min) | 16,600 | 0.33 |
| EGD5F5 | sediment | 24,600 | 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vite, G.; Lopez-Godoy, S.; Díaz-Leyva, P.; Kozina, A. Improving the Size Distribution of Polymeric Oblates Fabricated by the Emulsion-in-Gel Deformation Method. Colloids Interfaces 2023, 7, 50. https://doi.org/10.3390/colloids7030050
Vite G, Lopez-Godoy S, Díaz-Leyva P, Kozina A. Improving the Size Distribution of Polymeric Oblates Fabricated by the Emulsion-in-Gel Deformation Method. Colloids and Interfaces. 2023; 7(3):50. https://doi.org/10.3390/colloids7030050
Chicago/Turabian StyleVite, Giselle, Samuel Lopez-Godoy, Pedro Díaz-Leyva, and Anna Kozina. 2023. "Improving the Size Distribution of Polymeric Oblates Fabricated by the Emulsion-in-Gel Deformation Method" Colloids and Interfaces 7, no. 3: 50. https://doi.org/10.3390/colloids7030050
APA StyleVite, G., Lopez-Godoy, S., Díaz-Leyva, P., & Kozina, A. (2023). Improving the Size Distribution of Polymeric Oblates Fabricated by the Emulsion-in-Gel Deformation Method. Colloids and Interfaces, 7(3), 50. https://doi.org/10.3390/colloids7030050