1. Introduction
Brushing with bonded abrasives is an industrial manufacturing process, which is predominantly used for the deburring and rounding of metallic workpiece edges. Furthermore, it has gained importance in the finishing of technical surfaces, mainly for the reduction of the surface roughness [
1,
2,
3]. The process is characterized by its flexible brushing tools (
Figure 1), usually consisting of a cast epoxy brush body, to which abrasive filaments are attached (
Figure 1a). These are composed of an extruded polymer matrix, normally polyamide 6.12, and bonded abrasive grains, normally silicon carbide (SiC) or aluminum(III) oxide (Al
2O
3). However, especially during the finishing of ceramic workpieces, hard abrasives, such as diamond or cubic boron nitride (cBN), are required [
1,
4].
The advantages of brushing with bonded abrasives are based on the high flexibility of the abrasive filaments, which allow for the adaptation to complex workpiece geometries, despite ordinarily shaped tools, and therefore the compensation of small geometric deviations of tools, workpieces and machine systems, as well as tool trajectories. Additional advantages are low process forces and temperatures, and also the potential utilization of pre-existing machine systems designed for grinding and milling operations. A considerable disadvantage of the process is the insufficient knowledge of the motion, the chipping, and the wear behavior of the abrasive filaments, with the result that industrial processes are typically based on experiential values, making predictions for new processes difficult [
1,
5,
6].
Regarding the tool specific parameters most relevant for achieving a low workpiece surface roughness, small filament diameters d
f, large filament lengths l
f, and small grain sizes d
g, are needed, whereas contrary tool specifications are required for high material removal rates [
3,
7,
8]. A large brush body radius r
g leads to a larger number of filaments N
f and to a more enhanced support between filaments than a small brush body radius r
g, and thereby to more efficient brushing processes. The essential process parameters are the brushing velocity v
b, the tangential feed rate v
ft, and the penetration depth a
e (
Figure 1b). Above all, the surface roughness of the workpieces can be successively reduced by multiple brushing cycles until a lower roughness limit is reached, which is primarily dependent on the tool specification. Therefore, a low surface roughness can also be achieved with gentle process parameters, specifically low brushing velocities v
b, high tangential feed rates v
ft, and low penetration depths a
e [
3]. Furthermore, process heat can be dissipated by the use of cooling lubricant to prevent the melting of the abrasive filaments, which would affect the productivity adversely or even cause permanent tool damage. However, in some studies, a reduction of the productivity during brushing with cooling lubricant is mentioned, likely caused by a reduction of the effective Young modulus E
f of the abrasive filaments due to polyamide being prone to liquid absorption [
2,
3]. Within the scope of this article, productivity is defined as the rate of change of the work result, meaning the surface roughness or the material removal rate, while simultaneously considering the negative influence of tool wear.
Various studies confirm a significant dependence of the productivity on the applied contact forces, as high contact forces increase the penetration of the workpiece material by the abrasive grains [
1,
2,
3,
5,
6,
9]. To gain an understanding of the process behavior of abrasive filaments, technological investigations with single filaments and full brushing tools may be carried out, as well as numerical process simulations based on physical models. In both cases, the knowledge transfer between single-and multi-filament models is challenging and a focus of contemporary research [
9]. For example, contact force measurements with single filaments at high brushing velocities v
b are difficult (
Figure 1c), due to low force values along with a high predisposition of the experimental equipment towards unwanted vibrations. Adversely, the use of numerical process models for the calculation of a multitude of interacting filaments is still limited due to long computation times [
9].
Hence, the aim of this article is the introduction of a new method to correlate the numerically simulated contact forces of single abrasive filaments with the experimentally determined process forces of full brushing tools, the acquisition of which is relatively unproblematic. For this purpose, the contact impulse transmitted by the abrasive filaments onto the workpiece is calculated in order to avoid the use of error-sensitive smoothing algorithms and thus to increase the scope of application for numerically simulated brushing parameters.
2. Materials and Methods
The chosen case of application was the surface finishing of zirconium dioxide, partially stabilized with magnesium oxide (MgO-PSZ, or ZrO
2 for simplicity), its main domains of application including dental and medical engineering as well as industrial furnace linings [
10,
11]. The previously surface-ground workpieces feature dimensions of 200 × 200 × 200 mm
3 and an average roughness of Ra = 1.1 µm.
The brushing tools used were round brushes manufactured by C.Hilzinger-Thum GmbH and Co.KG, Tuttlingen, Germany, with a brush body radius of r
g = 140 mm, a tool width of b
b = 20 mm, a filament length of l
f = 40 mm, a filament diameter of d
f = 1.18 mm and a filament density of ρ
f = 1.11 g/cm³. Due to the high hardness and the brittle machining behavior of ZrO
2, abrasive filaments composed of polyamide 6.12 and bonded polycrystalline diamond with a grit size of 320 mesh and a mean grain size of d
g = 29.2 µm were used [
12]. Based on photographs of the brushing tools’ circumferences, an estimated number of abrasive filaments per tool of N
f = 10,500 ± 600 was determined. For this, a Hough transformation was applied to detect and count the circular filament tips of tool segments, extrapolating their quantity for the entire brushing tool.
The technological investigations were carried out on a plane and profile grinding machine of type Profimat MT 408 HTS, manufactured by Blohm Jung GmbH, Hamburg, Germany, and process forces were measured with a quartz three-component dynamometer of type 9257B, manufactured by Kistler Instrumente AG, Winterthur, Switzerland, to which the workpieces were attached. Because the workpieces were planar and edge contacts were not being investigated, only the process forces in the normal direction of the workpiece surface were evaluated; their arithmetic mean value over the processing time tp being defined as the tool contact normal force Fn,w. Despite the low heat conductivity of ZrO2, no cooling lubricant was used during brushing in order to decrease the number of possible influences on the measurement of process forces.
To simulate the deformations and the contact forces of abrasive filaments, a multi-body system based on the Lagrange formalism was implemented in MATLAB R2019b, developed by The MathWorks, Inc., Natick, Massachusetts, USA. Using spherical coordinates, the flexible filaments were subdivided into rigid segments, connected end-to-end by rotational springs and dampers. After the appropriate reduction of the degrees of freedom, the positions and the motions of the segments in three-dimensional space were distinctly characterized by their minimal coordinates, namely their polar angles φ
k and azimuth angles θ
k, as well as their respective angular velocities and accelerations. Incorporating the Lagrange function L, the kinetic energy E
kin, the potential energy E
pot, the dissipation energy D, and the conservative momentum M
k,φ, a system of ordinary differential equations of second was formed, which could be solved numerically. Equation (1) shows the differential equation used to calculate the polar angle φ
k of an arbitrary single segment with index k, while the azimuth angle θ
k was obtained analogously [
9].
The results indicate that the calculated process forces do not vary significantly for segment numbers of n ≥ 25, so that n = 25 was chosen as a compromise between high accuracy and low computation time. By the introduction of a rotating brush body and a translationally moved workpiece in the form of boundary conditions, the contact between abrasive filaments and arbitrary workpieces can be simulated in three-dimensional space. To subsequently characterize the contact behavior, a nominal contact length l
d was defined, which can be deduced from the contact angle Ω
c (
Figure 2). Depending on the tool specification and process parameters, abrasive filaments may exhibit dynamic oscillatory behavior following the initial workpiece contact, which leads to the bouncing of the filament tips on the workpiece surface. Therefore, the actual contact length l
c was calculated as the overall sum of the single contact lengths l
c,i.
Analogously to the nominal contact length l
d and the actual contact length l
c, the nominal contact time t
d and the actual contact time t
c were calculated, within which a filament tip was moved across the respective distance. Both the contact length l
c and the contact time t
c can be calculated from the contact normal force F
n, under the consideration that time steps without a filament–workpiece contact yield a contact normal force of F
n = 0 N (
Figure 3). Due to the contact time t
c being highly dependent on the brushing velocity v
b and the penetration depth a
e, the contact time ratio ε
tc was introduced on the grounds of interpretability (Equation (2)). It corresponds to a dimensionless normalization of the contact time t
c by the nominal contact time t
d and serves as a basis upon which to characterize filament motions as either striking (ε
tc → 0) or sweeping (ε
tc → 1).
It should also be noted that the contact time ratio εtc equals the analogously calculated contact length ratio εlc, assuming a constant time step width Δt. Nonetheless, the contact time ratio εtc was used within the scope of this article due to the contact normal impulse pn being based on the contact time tc and not the contact length lc (Equation (3)).
With regard to the dynamic oscillatory behavior of the abrasive filaments, the contact time ratio ε
tc is most likely a more robust measure than the previously established maximum filament tip deflection s
n,max, meaning the maximum absolute value of the shortest distance between deflected filament tip and undeformed filament during the filament-workpiece contact [
13] (
Figure 1c). Its main disadvantage becomes apparent while studying the curve shape of the filament tip deflection s
n over time t (
Figure 3), which may fluctuate considerably during the workpiece contact, where the deflection maximum is located. However, the maximum filament tip deflection s
n,max lacks usable information about the workpiece contact itself, which would be crucial in order to understand the effects of highly dynamic filament behavior on the productivity.
Further examination of the contact normal force F
n reveals that a meaningful maximum value is not easily deduced, because the curve shape is characterized by extreme peaks and a multitude of contact-free regions (
Figure 3), which can be attributed to the dynamic oscillatory behavior of the abrasive filaments as well as to their complex deformation [
13,
14]. Potential smoothing algorithms, such as median or Gaussian filters, would thereby lead to significant deviations and consequently distort the curve shape. While the contact normal force F
n shows consistent, steadily increasing curve shapes at low brushing velocities v
b [
13], the described dynamic behavior necessitates novel methods of evaluation, especially for high, industrially relevant brushing velocities v
b.
Therefore, the contact normal force F
n was converted into the contact normal impulse p
n, (Equation (3)) [
15]. Formally, the contact normal force F
n of a single abrasive filament was integrated over the contact time t
c. Because contact forces for both the process model and after experimental data acquisition exist in the form of discrete values with distinct indices i, the overall sum of all values F
n,i and subsequent multiplication with the time step width Δt can be used for this purpose.
As for the inverse transform, dividing the contact normal impulse p
n by the contact time t
c yields the equivalent contact normal force
(Equation (4)), which represents an arithmetic averaging of the contact normal force F
n over the contact time t
c.
To further project this method, which is only valid for single abrasive filaments, onto full brushing tools, the contact normal impulse p
n was multiplied with the estimated number of filaments N
f and the angular velocity ω to calculate the tool contact normal force F
n,w (Equation (5)).
Physically, the tool contact normal force Fn,w corresponds to the tool contact normal impulse pn,w transmitted by the brushing tool onto the workpiece over the course of a single second. It represents an extrapolation of a single abrasive filament while neglecting filament interactions, but shows robust behavior compared to typical smoothing algorithms if applied to abrasive filament contact forces.
3. Results
Utilizing the multi-body system based on the Lagrange formalism, a total of 120 contact simulations were computed, each modeling the contact between a single abrasive filament and a planar workpiece of ZrO2, while considering brushing velocities of vb ≤ 30 m/s and penetration depths of ae ≤ 5 mm. The tangential feed rate vft was not varied, as it was not expected to have an influence due to the plain workpiece geometry, no tangential or friction forces being investigated, and the tangential feed rate vft being several orders of magnitude smaller than the brushing velocity vb.
The maximum filament tip displacement s
n,max, used to monitor dynamic oscillatory filament behavior during previous research [
14], increases approximately linearly with the brushing velocity v
b and degressively with the penetration depth a
e (
Figure 4a) but otherwise provides insufficient information about the filament–workpiece contact due to the absence of a time dependent component. The corresponding contact time t
c shows a highly regressive decrease with increased brushing velocity v
b (
Figure 4b), although this effect is more prevalent for large penetration depths a
e than for small penetration depths a
e because of the increased contact angle Ω
c (
Figure 2). This implies that the brushing velocity v
b has a considerably greater impact on the contact time t
c, as well as on subsequently calculated parameters, than the penetration depth a
e.
For a more suitable visualization, the contact time t
c was divided by the nominal contact time t
d to calculate the contact time ratio ε
tc (Equation (2),
Figure 5). Variation of the process parameters shows that high brushing velocities v
b lead to primarily striking filament motions (ε
tc → 0) because abrasive filaments, deflected by an initial workpiece contact, are moved past the contact zone before they can swing back. In addition, an approximately proportional separating line between brushing velocity v
b and penetration depth a
e can be observed, below which filament motions are primarily striking, and above which the primarily sweeping region is characterized by a distinguishable tier.
In theory, dynamic oscillatory behavior and subsequent striking filament motions lead to an increase of the process forces and thereby to an increase of the material removal rate [
16,
17,
18,
19]. Although dynamic behavior can be both confirmed and controlled based on technological investigations, a positive influence on productivity remains to be confirmed. Nonetheless, the knowledge of the contact time ratio ε
tc might prospectively be utilized to predict the productivity of abrasive brushing processes. However, further technological investigations need to be carried out to verify this.
Comparing the contact normal impulses p
n of a single abrasive filament for varied process parameters, a regressive dependence on the brushing velocity v
b can be observed, particularly for high penetration depths a
e (
Figure 6a). Similar to the contact time ratio ε
tc, although less distinct, a tier is formed along the proportional line between brushing velocity v
b and penetration depth a
e, below which the contact normal impulse p
n is low. Except for the tier, the contact normal impulse p
n qualitatively resembles the contact time t
c (
Figure 4b) indicating that the contact normal force F
n affects the contact normal impulse p
n considerably less than the contact time t
c, Equation (3).
To explain the contradictory phenomenon where high brushing velocities v
b lead to low impulse transmissions and therefore to decreased productivity, the tool contact normal force F
n,w is calculated with regard to angular velocity ω and the estimated number of filaments N
f (Equation (5)).
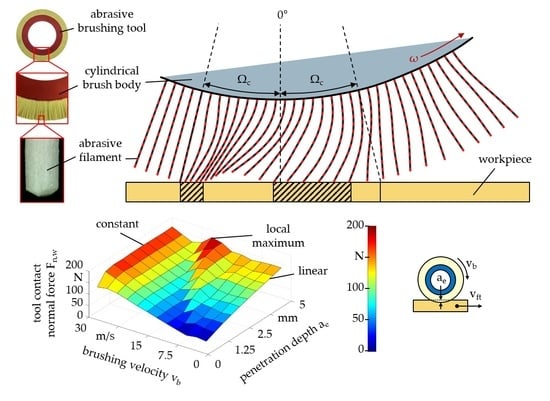
Figure 6b illustrates that high brushing velocities v
b amount to a higher tool contact normal force F
n,w than low brushing velocities v
b, because the total number of filament–workpiece contacts increases more rapidly with increasing angular velocity ω than the impulse transmitted by a single filament decreases. Equally noticeable is that the tool contact normal force F
n,w only shows a linear increase with the penetration depth a
e for low brushing velocities v
b. This gives the assumption that, contrary to previous research, high brushing velocities v
b, together with large penetration depths a
e, may lead to unproductive brushing processes due to both parameters substantially contributing to tool wear [
1,
3,
14].
Moreover, the tier observed in
Figure 5 and
Figure 6a results in a local maximum of the tool contact normal force F
n,w (
Figure 6b) likely caused by a second contact area towards the end of the filament–workpiece contact. This local maximum might be targeted by means of appropriate process design, in order to maximize the impulse transmission with only moderate brushing velocities v
b. To what extent this phenomenon has an impact on productivity remains to be determined by additional technological investigations.
Comparing the computed tool contact normal force F
n,w with the experimentally determined values, the variation of the brushing velocity v
b shows that the fundamental behavior is reflected by the model, although all investigated brushing velocities v
b lead to deviations outside of the experimentally determined standard deviation (
Figure 7a). Regarding the penetration depth a
e, the experimentally determined results show a dependence that is not predicted by the model within the investigated parameter boundaries (
Figure 7b).
In both cases, the most plausible cause of error may be the neglection of the filament interactions, because the computation of the tool contact normal force Fn,w is solely based on the extrapolation of a single abrasive filament. For large penetration depths ae, it is expected that abrasive filaments with either striking or sweeping motion behavior may be pressed onto the workpiece surface by neighboring filaments, which would increase the impulse transmission and thereby the process forces. Additional possible error causes could be undetected manufacturing inaccuracies of the brushing tools as well as a slight waviness of the abrasive filaments purposely induced by the manufacturer but not considered for the model, for which perfectly cylindrical filaments are assumed. Furthermore, the filament–workpiece contact is merely modeled for undeformed abrasive filaments, starting shortly before the initial contact in order to minimize computation times, whereas subsequent tool rotations and filament workpiece contacts at high brushing velocities vb might cause the abrasive filaments to already be deflected.