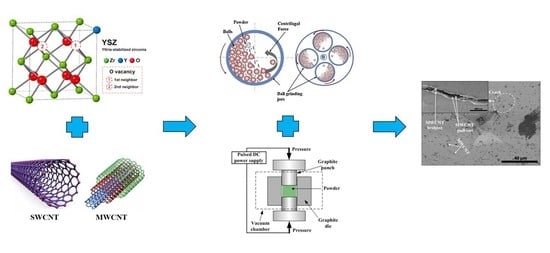
Zirconia-Based Ceramics Reinforced by Carbon Nanotubes: A Review with Emphasis on Mechanical Properties
Abstract
:1. Introduction
2. Zirconia Matrix: An Overview
2.1. Phase Diagram
2.2. Phase Transformation
2.3. Ionic Conductivity of Yttria-Stabilized Zirconia (YSZ)
3. Carbon Nanotubes (CNTs): A Valuable Second Phase in Zirconia-Based Composites
Synthesis of CNTs
4. Processing Techniques Used to Produce CNT-Reinforced Zirconia-Based Nanocomposites
4.1. Ball Milling
4.2. Spark Plasma Sintering
4.3. Other Possible Manufacturing Approaches
5. Mechanical Testing Methods and Properties of CNT/Zirconia and Ceramic-Matrix Composites
5.1. Comparative Stress–Strain Curves between Pure Ceramics and CMCs
5.2. Fracture Toughness
5.3. Hardness Testing
5.4. Estimation of Fracture Toughness in CMCs through Indentation Tests
5.5. Bending Strength Testing
5.6. Mechanical Properties of CNT-Reinforced Zirconia-Matrix Composites
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Krupka, M.; Kienzle, A. Fiber Reinforced Ceramic Composite for Brake Discs. In Proceedings of the 18th Annual Brake Colloquium & Engineering Display, San Diego, CA, USA, 1–4 October 2000. [Google Scholar]
- Hardwicke, C.U.; Lau, Y.-C. Advances in thermal spray coatings for gas turbines and energy generation: A review. J. Therm. Spray Technol. 2013, 22, 564–576. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Z.; Liu, M. Characterization of sulfur poisoning of Ni–YSZ anodes for solid oxide fuel cells using in situ Raman microspectroscopy. Solid State Ion. 2007, 178, 925–935. [Google Scholar] [CrossRef]
- Pramanik, S.; Manna, A.; Tripathy, A.; Kar, K.K. Current advancements in ceramic matrix composites. In Composite Materials, 1st ed.; Kar, K., Ed.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 457–496. [Google Scholar]
- Niihara, K. New design concept of structural ceramics-ceramic nanocomposites. J. Ceram. Soc. Jpn. 1991, 99, 974–982. [Google Scholar] [CrossRef] [Green Version]
- Porwal, H.; Saggar, R. Ceramic matrix nanocomposites. In Comprehensive Composite Materials II, 2nd ed.; Beaumont, P.W.R., Zweben, C.H., Eds.; Elsevier Ltd.: London, UK, 2018; pp. 138–161. [Google Scholar]
- Silvestre, J.; Silvestre, N.; de Brito, J. An overview on the improvement of mechanical properties of ceramics nanocomposites. J. Nanomater. 2015, 2015, 106494. [Google Scholar] [CrossRef] [Green Version]
- Wu, H. Understanding residual stresses and fracture toughness in ceramic nanocomposites. In Residual Stresses in Composite Materials, 1st ed.; Shokrieh, M.M., Ed.; Woodhead Publishing Limited: Sawston, UK, 2014; pp. 256–292. [Google Scholar]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Aqel, A.; Abou El-Nour, K.M.M.; Ammar, R.A.A.; Al-Warthan, A. Carbon nanotubes, science and technology part (I) structure, synthesis and characterisation. Arab. J. Chem. 2012, 5, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Kuntz, J.D.; Zhan, G.-D.; Mukherjee, A.K. Nanocrystalline-matrix ceramic composites for improved fracture toughness. MRS Bull. 2004, 29, 22–27. [Google Scholar] [CrossRef]
- Maiti, T.K.; Majhi, J.; Maiti, S.K.; Singh, J.; Dixit, P.; Rohilla, P.; Ghosh, S.; Bhushan, S.; Chattopadhyay, S. Zirconia- and ceria-based electrolytes for fuel cell applications: Critical advancements toward sustainable and clean energy production. Environ. Sci. Pollut. Res. 2022, 29, 64489–64512. [Google Scholar] [CrossRef]
- Yin, L.; Nakanishi, Y.; Alao, A.-R.; Song, X.-F.; Abduo, J.; Zhang, Y. A review of engineered zirconia surfaces in biomedical applications. Procedia CIRP 2017, 65, 284–290. [Google Scholar] [CrossRef]
- Bistolfi, A.; Ferracini, R.; Lee, G.C.; Mellano, D.; Guidotti, C.; Baino, F.; Verné, E. Ceramic-on-ceramic catastrophic liner failure in total hip arthroplasty: Morphological and compositional analysis of fractured ceramic components. Ceram. Int. 2021, 47, 11029–11036. [Google Scholar] [CrossRef]
- Sternitzke, M. Structural ceramic nanocomposites. J. Eur. Ceram. Soc. 1997, 17, 1061–1082. [Google Scholar] [CrossRef]
- Navrotsky, A. Thermochemical insights into refractory ceramic materials based on oxides with large tetravalent cations. J. Mater. Chem. 2005, 15, 1883–1890. [Google Scholar] [CrossRef]
- Denry, I.; Kelly, J.R. State of the art of zirconia for dental applications. Dent. Mater. 2008, 24, 299–307. [Google Scholar] [CrossRef]
- Padture, N.P.; Gell, M.; Jordan, E.H. Thermal barrier coatings for gas-turbine engine applications. Science 2002, 296, 280–284. [Google Scholar]
- Farid, S.B.H. Structure, microstructure, and properties of bioceramics. In Bioceramics: For Materials Science and Engineering, 1st ed.; Elsevier Ltd.: London, UK, 2019; pp. 39–76. [Google Scholar]
- Vagkopoulou, T.; Koutayas, S.O.; Koidis, P.; Strub, J.R. Zirconia in dentistry: Part 1. Discovering the nature of an upcoming bioceramic. Eur. J. Esthet. Dent. 2009, 4, 130–151. [Google Scholar]
- Hannink, R.H.J.; Kelly, P.M.; Muddle, B.C. Transformation toughening in zirconia-containing ceramics. J. Am. Ceram. Soc. 2000, 83, 461–487. [Google Scholar] [CrossRef]
- Evans, A.G.; Mumm, D.R.; Hutchinson, J.W.; Meier, G.H.; Pettit, F.S. Mechanisms controlling the durability of thermal barrier coatings. Prog. Mater. Sci. 2001, 46, 505–553. [Google Scholar] [CrossRef]
- Piconi, C.; Maccauro, G. Zirconia as a ceramic biomaterial. Biomaterials 1999, 20, 1–25. [Google Scholar] [CrossRef]
- Li, P.; Chen, I.-W.; Penner-Hahn, J.E. Effect of dopants on zirconia stabilization—An X-ray absorption study: III, charge-compensating dopants. J. Am. Ceram. Soc. 1994, 77, 1289–1295. [Google Scholar]
- Green, D.J.; Hannink, R.H.J.; Swain, M.V. Transformation Toughening of Ceramics, 1st ed.; CRC Press: Boca Raton, FL, USA, 1989; pp. 1–240. [Google Scholar]
- Scott, H.G. Phase relationships in the zirconia-yttria system. J. Mater. Sci. 1975, 10, 1527–1535. [Google Scholar] [CrossRef]
- Witz, G.; Shklover, V.; Steurer, W.; Bachegowda, S.; Bossmann, H.-P. Phase evolution in yttria-stabilized zirconia thermal barrier coatings studied by Rietveld refinement of X-ray powder diffraction patterns. J. Am. Ceram. Soc. 2007, 90, 2935–2940. [Google Scholar] [CrossRef]
- Zhu, Y.-F.; Shi, L.; Liang, J.; Hui, D.; Lau, K.-T. Synthesis of zirconia nanoparticles on carbon nanotubes and their potential for enhancing the fracture toughness of alumina ceramics. Compos. Part B 2008, 39, 1136–1141. [Google Scholar] [CrossRef]
- Darolia, R. Thermal barrier coatings technology: Critical review, progress update, remaining challenges and prospects. Int. Mater. Rev. 2013, 58, 315–348. [Google Scholar] [CrossRef]
- Mercer, C.; Williams, J.R.; Clarke, D.R.; Evans, A.G. On a ferroelastic mechanism governing the toughness of metastable tetragonal-prime (t′) yttria-stabilized zirconia. Proc. R. Soc. A Math. Phys. Eng. Sci. 2007, 463, 1393–1408. [Google Scholar] [CrossRef]
- Garvie, R.C.; Hannink, R.H.; Pascoe, R.T. Ceramic steel? Nature 1975, 258, 703–704. [Google Scholar] [CrossRef]
- Wolten, G.M. Diffusionless phase transformations in zirconia and hafnia. J. Am. Ceram. Soc. 1963, 46, 418–422. [Google Scholar] [CrossRef]
- Budiansky, B.; Hutchinson, J.W.; Lambropoulos, J.C. Continuum theory of dilatant transformation toughening in ceramics. Int. J. Solids Struct. 1983, 19, 337–355. [Google Scholar] [CrossRef]
- Green, D.J.; Nicholson, P.S.; Embury, J.D. Fracture toughness of a partially stabilized ZrO2 in the system CaO-ZrO2. J. Am. Ceram. Soc. 1973, 56, 619–623. [Google Scholar] [CrossRef]
- Evans, A.G.; Faber, K.T. Crack-growth resistance of microcracking brittle materials. J. Am. Ceram. Soc. 1984, 67, 255–260. [Google Scholar] [CrossRef]
- Xiao, Z.; Kerner, R.A.; Zhao, L.; Tran, N.L.; Lee, K.M.; Koh, T.-W.; Scholes, G.D.; Rand, B.P. Efficient perovskite light-emitting diodes featuring nanometre-sized crystallites. Nat. Photonics 2017, 11, 108–115. [Google Scholar] [CrossRef]
- Kelly, J.R.; Denry, I. Stabilized zirconia as a structural ceramic: An overview. Dent. Mater. 2008, 24, 289–298. [Google Scholar] [CrossRef] [PubMed]
- Subbarao, E.C.; Maiti, H.S.; Srivastava, K.K. Martensitic transformation in zirconia. Phys. Status Solidi A 1974, 21, 9–40. [Google Scholar] [CrossRef]
- Manning, P.S.; Sirman, J.D.; De Souza, R.A.; Kilner, J.A. The kinetics of oxygen transport in 9.5 mol% single crystal yttria stabilised zirconia. Solid State Ion. 1997, 100, 1–10. [Google Scholar] [CrossRef]
- Kosacki, I.; Petrovsky, V.; Anderson, H.U. Modeling and characterization of electrical transport in oxygen conducting solid electrolytes. J. Electroceram. 2000, 4, 243–249. [Google Scholar] [CrossRef]
- Hearing, C.; Roosen, A.; Schichl, H. Degradation of the electrical conductivity in stabilised zirconia systems: Part I: Yttria-stabilised zirconia. Solid State Ion. 2005, 176, 253–259. [Google Scholar] [CrossRef]
- Tsampas, M.N.; Sapountzi, F.M.; Vernoux, P. Applications of yttria stabilized zirconia (YSZ) in catalysis. Catal. Sci. Technol. 2015, 5, 4884–4900. [Google Scholar] [CrossRef]
- Shi, H.; Su, C.; Ran, R.; Cao, J.; Shao, Z. Electrolyte materials for intermediate-temperature solid oxide fuel cells. Prog. Nat. Sci. Mater. Int. 2020, 30, 764–774. [Google Scholar] [CrossRef]
- Kroto, H.W.; Heath, J.R.; O’Brien, S.C.; Curl, R.F.; Smalley, R.E. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
- Wang, R.; Tao, J.; Yu, B.; Dai, L. Characterization of multiwalled carbon nanotube-polymethyl methacrylate composite resins as denture base materials. J. Prosthet. Dent. 2014, 111, 318–326. [Google Scholar] [CrossRef]
- Kumar, M.; Ando, Y. Chemical vapor deposition of carbon nanotubes: A review on growth mechanism and mass production. J. Nanosci. Nanotechnol. 2010, 10, 3739–3758. [Google Scholar] [CrossRef] [Green Version]
- Thostenson, E.T.; Ren, Z.; Chou, T. Advances in the science and technology of carbon nanotubes and their composites: A review. Compos. Sci. Technol. 2001, 61, 1899–1912. [Google Scholar] [CrossRef] [Green Version]
- Melk, L. Processing and Properties of Zirconia-CNT Composites. Doctoral Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, May 2016. [Google Scholar]
- Loos, M. Production of CNTs and risks to health. In Carbon Nanotube Reinforced Composites: CNT Polymer Science and Technology, 1st ed.; Elsevier Inc.: New York City, NY, USA, 2015; pp. 103–123. [Google Scholar]
- Chan, K.F.; Zaid, M.H.M.; Mamat, M.S.; Liza, S.; Tanemura, M.; Yaakob, Y. Recent developments in carbon nanotubes-reinforced ceramic matrix composites: A review on dispersion and densification techniques. Crystals 2021, 11, 457. [Google Scholar] [CrossRef]
- Sharma, P.; Sharma, S.; Khanduja, D. On the use of ball milling for the production of ceramic powders. Mater. Manuf. Process. 2015, 30, 1370–1376. [Google Scholar] [CrossRef]
- Tangsathitkulchai, C. Acceleration of particle breakage rates in wet batch ball milling. Powder Technol. 2002, 124, 67–75. [Google Scholar] [CrossRef]
- Janot, R.; Guérard, D. Ball-milling: The behavior of graphite as a function of the dispersal media. Carbon 2002, 40, 2887–2896. [Google Scholar] [CrossRef]
- Shi, S.-L.; Liang, J. Effect of multiwall carbon nanotubes on electrical and dielectric properties of yttria-stabilized zirconia ceramic. J. Am. Ceram. Soc. 2006, 89, 3533–3535. [Google Scholar] [CrossRef]
- Zhou, J.P.; Gong, Q.M.; Yuan, K.Y.; Wu, J.J.; Chen, Y.F.; Li, C.S.; Liang, J. The effects of multiwalled carbon nanotubes on the hot-pressed 3 mol% yttria stabilized zirconia ceramics. Mater. Sci. Eng. A 2009, 520, 153–157. [Google Scholar] [CrossRef]
- Chintapalli, R.K.; Marro, F.G.; Milson, B.; Reece, M.; Anglada, M. Processing and characterization of high-density zirconia–carbon nanotube composites. Mater. Sci. Eng. A 2012, 549, 50–59. [Google Scholar] [CrossRef]
- Lamnini, S.; Fogarassy, Z.; Horváth, Z.E.; Tóth, S.; Balázsi, K.; Balázsi, C. The role of the attrition milling on the grain size and distribution of the carbon nanotubes in YSZ powders. Bol. Soc. Esp. Ceram. Vidrio 2019, 58, 126–133. [Google Scholar] [CrossRef]
- Rajeswari, K.; Hareesh, U.S.; Subasri, R.; Chakravarty, D.; Johnson, R. Comparative evaluation of spark plasma (SPS), microwave (MWS), two stage sintering (TSS) and conventional sintering (CRH) on the densification and micro structural evolution of fully stabilized zirconia ceramics. Sci. Sinter. 2010, 42, 259–267. [Google Scholar] [CrossRef]
- Munir, Z.A.; Anselmi-Tamburini, U.; Ohyanagi, M. The effect of electric field and pressure on the synthesis and consolidation of materials: A review of the spark plasma sintering method. J. Mater. Sci. 2006, 41, 763–777. [Google Scholar] [CrossRef]
- Inoue, K. Electric-Discharge Sintering. U.S. Patent 3241956A, 22 March 1966. [Google Scholar]
- Guillon, O.; Gonzalez-Julian, J.; Dargatz, B.; Kessel, T.; Schierning, G.; Räthel, J.; Herrmann, M. Field-assisted sintering technology/spark plasma sintering: Mechanisms, materials, and technology developments. Adv. Eng. Mater. 2014, 16, 830–849. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Yan, H.; Reece, M.J.; Jiang, K. Toughening of zirconia/alumina composites by the addition of graphene platelets. J. Eur. Ceram. Soc. 2012, 32, 4185–4193. [Google Scholar] [CrossRef]
- Suárez, M.; Fernández, A.; Menéndez, J.L.; Torrecillas, R.; Kessel, H.U.; Hennicke, J.; Kirchner, R.; Kessel, T. Challenges and opportunities for spark plasma sintering: A key technology for a new generation of materials. In Sintering Applications, 1st ed.; Ertuğ, B., Ed.; IntechOpen: Rijeka, Croatia, 2013; pp. 319–342. [Google Scholar]
- Anselmi-Tamburini, U.; Garay, J.E.; Munir, Z.A.; Tacca, A.; Maglia, F.; Spinolo, G. Spark plasma sintering and characterization of bulk nanostructured fully stabilized zirconia: Part I. Densification studies. J. Mater. Res. 2004, 19, 3255–3262. [Google Scholar] [CrossRef]
- Anselmi-Tamburini, U.; Garay, J.E.; Munir, Z.A. Fast low-temperature consolidation of bulk nanometric ceramic materials. Scr. Mater. 2006, 54, 823–828. [Google Scholar] [CrossRef]
- Asoka-Kumar, P.; O’Brien, K.; Lynn, K.G.; Simpson, P.J.; Rodbell, K.P. Detection of current-induced vacancies in thin aluminum-copper lines using positrons. Appl. Phys. Lett. 1996, 68, 406–408. [Google Scholar] [CrossRef]
- Bernard-Granger, G.; Guizard, C.; Surblé, S.; Baldinozzi, G.; Addad, A. Spark plasma sintering of a commercially available granulated zirconia powder—II. Microstructure after sintering and ionic conductivity. Acta Mater. 2008, 56, 4658–4672. [Google Scholar] [CrossRef]
- Skandan, G.; Hahn, H.; Kear, B.H.; Roddy, M.; Cannon, W.R. The effect of applied stress on densification of nanostructured zirconia during sinter-forging. Mater. Lett. 1994, 20, 305–309. [Google Scholar] [CrossRef]
- Chen, W.; Anselmi-Tamburini, U.; Garay, J.E.; Groza, J.R.; Munir, Z.A. Fundamental investigations on the spark plasma sintering/synthesis process: I. Effect of dc pulsing on reactivity. Mater. Sci. Eng. A 2005, 394, 132–138. [Google Scholar] [CrossRef]
- Robles Arellano, K.D.; Bichler, L.; Akkiraju, K.; Fong, R.; Mondal, K. Densification behavior of Spark Plasma Sintered La2O3–YSZ ceramic composites. Ceram. Int. 2014, 40, 715–722. [Google Scholar] [CrossRef]
- Mazaheri, M.; Mari, D.; Schaller, R.; Bonnefont, G.; Fantozzi, G. Processing of yttria stabilized zirconia reinforced with multi-walled carbon nanotubes with attractive mechanical properties. J. Eur. Ceram. Soc. 2011, 31, 2691–2698. [Google Scholar] [CrossRef]
- Karanam, A.; Bichler, L.; Fong, R. On the densification behavior of (0.2, 0.5, and 1 Wt Pct) CNT-YSZ ceramic composites processed via spark plasma sintering. Metall. Mater. Trans. B 2015, 46, 1666–1673. [Google Scholar] [CrossRef]
- Shahabuddin, M.; Madhar, N.A.; Alzayed, N.S.; Asif, M. Uniform dispersion and exfoliation of multi-walled carbon nanotubes in CNT-MgB2 superconductor composites using surfactants. Materials 2019, 12, 3044. [Google Scholar] [CrossRef] [Green Version]
- Rivero-Antúnez, P.; Cano-Crespo, R.; Esquivias, L.; De la Rosa-Fox, N.; Zamora-Ledezma, C.; Domínguez-Rodríguez, A.; Morales-Flórez, V. Mechanical characterization of sol-gel alumina-based ceramics with intragranular reinforcement of multiwalled carbon nanotubes. Ceram. Int. 2020, 46, 19723–19730. [Google Scholar] [CrossRef]
- Munz, D.; Fett, T. Ceramics: Mechanical Properties, Failure Behaviour, Materials Section, 1st ed.; Springer: Berling/Heidelberg, Germany, 1999; pp. 1–309. [Google Scholar]
- Sable, P.A.; LaJeunesse, J.; Sullivan, C.; Kamavaram, V.; Borg, J.P. Dynamic compaction of yttria-stabilized zirconia with the addition of carbon-nanotubes. AIP Conf. Proc. 2017, 1793, 120004. [Google Scholar]
- Timoshenko, S.; Goodier, J.N. Theory of Elasticity, 2nd ed.; McGraw Hill: New York City, NY, USA, 1951; pp. 1–506. [Google Scholar]
- Maynard, J. Resonant ultrasound spectroscopy. Phys. Today 1996, 49, 26–31. [Google Scholar] [CrossRef]
- Guttmann, G.M.; Gelbstein, Y. Mechanical properties of thermoelectric materials for practical applications. In Bringing Thermoelectricity into Reality, 1st ed.; Aranguren, P., Ed.; IntechOpen: Rijeka, Croatia, 2018; pp. 63–80. [Google Scholar]
- Wei, J.; Pećanac, G.; Malzbender, J. Review of mechanical characterization methods for ceramics used in energy technologies. Ceram. Int. 2014, 40, 15371–15380. [Google Scholar] [CrossRef]
- ASTM D2845-00; Standard Test Method for Laboratory Determination of Pulse Velocities and Ultrasonic Elastic Constants of Rock. ASTM International: West Conshohocken, PA, USA, 2000.
- Mahato, N.; Nisar, A.; Mohapatra, P.; Rawat, S.; Ariharan, S.; Balani, K. Effect of far-field stresses and residual stresses incorporation in predicting fracture toughness of carbon nanotube reinforced yttria stabilized zirconia. J. Appl. Phys. 2017, 122, 145104. [Google Scholar] [CrossRef]
- Chandler, H. Hardness Testing, 2nd ed.; ASM International: Almere, The Netherlands, 1999; pp. 1–192. [Google Scholar]
- Danzer, R.; Lube, T.; Morrell, R.; Supancic, P. Mechanical properties of ceramics. In Handbook of Advanced Ceramics: Materials, Applications, Processing, and Properties, 2nd ed.; Somiya, S., Ed.; Elsevier Inc.: New York City, NY, USA, 2013; pp. 609–632. [Google Scholar]
- Sergejev, F.; Antonov, M. Comparative study on indentation fracture toughness measurements of cemented carbides. Proc. Est. Acad. Sci. Eng. 2006, 12, 388–398. [Google Scholar]
- Sheikh, S.; M’Saoubi, R.; Flasar, P.; Schwind, M.; Persson, T.; Yang, J.; Llanes, L. Fracture toughness of cemented carbides: Testing method and microstructural effects. Int. J. Refract. Met. Hard Mater. 2015, 49, 153–160. [Google Scholar] [CrossRef] [Green Version]
- Shetty, D.K.; Wright, I.G.; Mincer, P.N.; Clauer, A.H. Indentation fracture of WC-Co cermets. J. Mater. Sci. 1985, 20, 1873–1882. [Google Scholar] [CrossRef]
- Aleksandrov Fabijanić, T.; Ćorić, D.; Šnajdar Musa, M.; Sakoman, M. Vickers indentation fracture toughness of near-nano and nanostructured WC-Co cemented carbides. Metals 2017, 7, 143. [Google Scholar] [CrossRef] [Green Version]
- Quinn, G.D. Fracture toughness of ceramics by the Vickers indentation crack length method: A critical review. In Mechanical Properties and Performance of Engineering Ceramics II: Ceramic Engineering and Science Proceedings, 1st ed.; Tandon, R., Wereszczak, A., Lara-Curzio, E., Eds.; Wiley-American Ceramic Society: Hoboken, NJ, USA, 2006; pp. 45–62. [Google Scholar]
- Cook, R.F.; Pharr, G.M. Direct observation and analysis of indentation cracking in glasses and ceramics. J. Am. Ceram. Soc. 1990, 73, 787–817. [Google Scholar] [CrossRef]
- Dowling, N.E. Mechanical Behavior of Materials: Engineering Methods for Deformation, Fracture, and Fatigue, 4th ed.; Pearson College Div: London, UK, 2012; pp. 1–936. [Google Scholar]
- Anderson, K.J. Hardness testing. MRS Bull. 1994, 19, 76–77. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.P.; Zhu, X.F.; Zhang, G.P.; Tan, J.; Wang, W.; Wu, B. Investigation of deformation instability of Au/Cu multilayers by indentation. Philos. Mag. 2010, 90, 3049–3067. [Google Scholar] [CrossRef]
- Zhang, P.; Li, S.X.; Zhang, Z.F. General relationship between strength and hardness. Mater. Sci. Eng. A 2011, 529, 62–73. [Google Scholar] [CrossRef]
- Bakhsh, N.; Khalid, F.A.; Hakeem, A.S. Synthesis and characterization of pressureless sintered carbon nanotube reinforced alumina nanocomposites. Mater. Sci. Eng. A 2013, 578, 422–429. [Google Scholar] [CrossRef]
- Yamamoto, G.; Omori, M.; Hashida, T.; Kimura, H. A novel structure for carbon nanotube reinforced alumina composites with improved mechanical properties. Nanotechnology 2008, 19, 315708. [Google Scholar] [CrossRef]
- Mo, C.B.; Cha, S.I.; Kim, K.T.; Lee, K.H.; Hong, S.H. Fabrication of carbon nanotube reinforced alumina matrix nanocomposite by sol-gel process. Mater. Sci. Eng. A 2005, 395, 124–128. [Google Scholar] [CrossRef]
- Morales-Rodríguez, A.; Gallardo-López, A.; Fernández-Serrano, A.; Poyato, R.; Muñoz, A.; Domínguez-Rodríguez, A. Improvement of Vickers hardness measurement on SWNT/Al2O3 composites consolidated by spark plasma sintering. J. Eur. Ceram. Soc. 2014, 34, 3801–3809. [Google Scholar] [CrossRef] [Green Version]
- Lamnini, S.; Károly, Z.; Bódis, E.; Balázsi, K.; Balázsi, C. Influence of structure on the hardness and the toughening mechanism of the sintered 8YSZ/MWCNTs composites. Ceram. Int. 2019, 45, 5058–5065. [Google Scholar] [CrossRef]
- Liu, J.; Guo, H.; Su, Y.; Wang, L.; Wei, L.; Yang, G.; Yang, Y.; Jiang, K. Spark plasma sintering of graphene platelet reinforced zirconia composites with improved mechanical performance. Mater. Sci. Eng. A 2017, 688, 70–75. [Google Scholar] [CrossRef]
- Zimmer, J.; Klein, D.; Stommel, M. Experimental and numerical analysis of liquid-forming. Key Eng. Mater. 2015, 651–653, 842–847. [Google Scholar] [CrossRef]
- Kaliszewski, M.S.; Behrens, G.; Heuer, A.H.; Shaw, M.C.; Marshall, D.B.; Dransmanri, G.W.; Steinbrech, R.W.; Pajares, A.; Guiberteau, F.; Cumbrera, F.L.; et al. Indentation studies on Y2O2-stabilized ZrO2: I, development of indentation-induced cracks. J. Am. Ceram. Soc. 1994, 77, 1185–1193. [Google Scholar] [CrossRef]
- Lube, T. Indentation crack profiles in silicon nitride. J. Eur. Ceram. Soc. 2001, 21, 211–218. [Google Scholar] [CrossRef]
- Hagan, J.T.; Swain, M.V. The origin of median and lateral cracks around plastic indents in brittle materials. J. Phys. D Appl. Phys. 1978, 11, 2091–2102. [Google Scholar] [CrossRef]
- Liu, S.-Y.; Chen, I.-W. Fatigue of yttria-stabilized zirconia: II, crack propagation, fatigue striations, and short-crack behavior. J. Am. Ceram. Soc. 1991, 74, 1206–1216. [Google Scholar] [CrossRef] [Green Version]
- Sglavo, V.M.; Pancheri, P. Crack decorating technique for fracture-toughness measurement in alumina. J. Eur. Ceram. Soc. 1997, 17, 1697–1706. [Google Scholar] [CrossRef]
- Liang, K.M.; Orange, G.; Fantozzi, G. Evaluation by indentation of fracture toughness of ceramic materials. J. Mater. Sci. 1990, 25, 207–214. [Google Scholar] [CrossRef]
- Xie, F.X.; Zhang, D.; Su, H.; Ren, X.; Wong, K.S.; Grätzel, M.; Choy, W.C.H. Vacuum-assisted thermal annealing of CH3NH3PbI3 for highly stable and efficient perovskite solar cells. ACS Nano 2015, 9, 639–646. [Google Scholar] [CrossRef]
- Hansen, J.J.; Cutler, R.A.; Shetty, D.K.; Virkar, A.V. Indentation fracture response and damage resistance of Al2O3-ZrO2 composites strengthened by transformation-induced residual stresses. J. Am. Ceram. Soc. 1988, 71, C-501–C-505. [Google Scholar]
- Cuadrado, N.; Casellas, D.; Llanes, L.; González, I.; Caro, J. Effect of Crystal Anisotropy on the Mechanical Properties of WC Embedded in WC-Co Cemented Carbides. In Proceedings of the Euro PM2011 Powder Metallurgy Congress & Exhibition, Barcelona, Spain, 10–12 October 2011. [Google Scholar]
- Shatov, A.V.; Ponomarev, S.S.; Firstov, S.A. Fracture and strength of hardmetals at room temperature. In Comprehensive Hard Materials, 1st ed.; Sarin, V.K., Ed.; Elsevier Ltd.: London, UK, 2014; pp. 301–343. [Google Scholar]
- Rodrigues Junior, S.A.; Ferracane, J.L.; Della Bona, Á. Flexural strength and Weibull analysis of a microhybrid and a nanofill composite evaluated by 3- and 4-point bending tests. Dent. Mater. 2008, 24, 426–431. [Google Scholar] [CrossRef]
- Jones, S.L.; Norman, C.J.; Shahani, R. Crack-profile shapes formed under a Vickers indent pyramid. J. Mater. Sci. Lett. 1987, 6, 721–723. [Google Scholar] [CrossRef]
- Evans, A.G.; Charles, E.A. Fracture toughness determinations by indentation. J. Am. Ceram. Soc. 1976, 59, 371–372. [Google Scholar] [CrossRef]
- Antis, G.R.; Chantikul, P.; Lawn, B.R.; Marsall, D.B. A critical evaluation of indentation techniques for measuring fracture toughness: I, direct crack measurements. J. Am. Ceram. Soc. 1981, 64, 533–538. [Google Scholar] [CrossRef]
- Marshall, D.B.; Lawn, B.R.; Evans, A.G. Elastic/plastic indentation damage in ceramics: The lateral crack system. J. Am. Ceram. Soc. 1982, 65, 561–566. [Google Scholar] [CrossRef]
- Zahedi, A.M.; Javadpour, J.; Rezaie, H.R.; Mazaheri, M. Analytical study on the incorporation of zirconia-based ceramics with carbon nanotubes: Dispersion methods and mechanical properties. Ceram. Int. 2016, 42, 1653–1659. [Google Scholar] [CrossRef]
- Melk, L.; Antti, M.-L.; Anglada, M. Material removal mechanisms by EDM of zirconia reinforced MWCNT nanocomposites. Ceram. Int. 2016, 42, 5792–5801. [Google Scholar]
- Zhan, G.-D.; Kuntz, J.D.; Wan, J.; Mukherjee, A.K. Single-wall carbon nanotubes as attractive toughening agents in alumina-based nanocomposites. Nat. Mater. 2003, 2, 38–42. [Google Scholar] [CrossRef]
- Wang, X.; Padture, N.P.; Tanaka, H. Contact-damage-resistant ceramic/single-wall carbon nanotubes and ceramic/graphite composites. Nat. Mater. 2004, 3, 539–544. [Google Scholar] [CrossRef]
- Gallardo-López, A.; Poyato, R.; Morales-Rodríguez, A.; Fernández-Serrano, A.; Muñoz, A.; Domínguez-Rodríguez, A. Hardness and flexural strength of single-walled carbon nanotube/alumina composites. J. Mater. Sci. 2014, 49, 7116–7123. [Google Scholar]
- Ast, J.; Ghidelli, M.; Durst, K.; Göken, M.; Sebastiani, M.; Korsunsky, A.M. A review of experimental approaches to fracture toughness evaluation at the micro-scale. Mater. Des. 2019, 173, 107762. [Google Scholar] [CrossRef]
- Arunkumar, T.; Anand, G.; Subbiah, R.; Karthikeyan, R.; Jeevahan, J. Effect of multiwalled carbon nanotubes on improvement of fracture toughness of spark-plasma-sintered yttria-stabilized zirconia nanocomposites. J. Mater. Eng. Perform. 2021, 30, 3925–3933. [Google Scholar]
- Vandewalle, L. Recommendations of RILEM TC 162-TDF: Test and design methods for steel fibre reinforced concrete. Mater. Struct. 2000, 33, 75–81. [Google Scholar]
- Hou, P.; Zhao, H.; Ma, Z.; Zhang, S.; Li, J.; Dong, X.; Sun, Y.; Zhu, Z. Influence of punch radius on elastic modulus of three-point bending tests. Adv. Mech. Eng. 2016, 8, 1–8. [Google Scholar]
- Jambagi, S.C.; Kar, S.; Brodard, P.; Bandyopadhyay, P.P. Characteristics of plasma sprayed coatings produced from carbon nanotube doped ceramic powder feedstock. Mater. Des. 2016, 112, 392–401. [Google Scholar] [CrossRef]
- Echeberria, J.; Rodríguez, N.; Vleugels, J.; Vanmeensel, K.; Reyes-Rojas, A.; Garcia-Reyes, A.; Domínguez-Rios, C.; Aguilar-Elguézabal, A.; Bocanegra-Bernal, M.H. Hard and tough carbon nanotube-reinforced zirconia-toughened alumina composites prepared by spark plasma sintering. Carbon 2012, 50, 706–717. [Google Scholar] [CrossRef]
- Gómez, S.; Rendtorff, N.M.; Aglietti, E.F.; Sakka, Y.; Estili, M.; Suárez, G. Heterocoagulation and SPS sintering of sulfonitric-treated CNT and 8YZ nanopowders. J. Asian Ceram. Soc. 2019, 7, 238–246. [Google Scholar]
- Thakare, J.G.; Pandey, C.; Mulik, R.S.; Mahapatra, M.M. Mechanical property evaluation of carbon nanotubes reinforced plasma sprayed YSZ-alumina composite coating. Ceram. Int. 2018, 44, 6980–6989. [Google Scholar]
- Song, N.; Liu, H.; Fang, J. Fabrication and mechanical properties of multi-walled carbon nanotube reinforced reaction bonded silicon carbide composites. Ceram. Int. 2016, 42, 351–356. [Google Scholar]
- Mazaheri, M.; Mari, D.; Hesabi, Z.R.; Schaller, R.; Fantozzi, G. Multi-walled carbon nanotube/nanostructured zirconia composites: Outstanding mechanical properties in a wide range of temperature. Compos. Sci. Technol. 2011, 71, 939–945. [Google Scholar] [CrossRef]
- Suresh, A.; Mayo, M.J.; Porter, W.D.; Rawn, C.J. Crystallite and grain-size-dependent phase transformations in yttria-doped zirconia. J. Am. Ceram. Soc. 2003, 86, 360–362. [Google Scholar] [CrossRef]
















| Matrix Material | Carbon Agent | CNT Content (vol% or wt%) | Hardness (GPa) | Fracture Toughness (MPa·m0.5) | Density ρ (g/cm3 or %) | Ref. |
|---|---|---|---|---|---|---|
| 8YSZ | - | - | ~13.49 | 2.6 | 6.02 g/cm3 | [99] |
| 8YSZ | MWCNTs | 1 wt% | ~12.44 | 3.2 | 6.76 g/cm3 | [99] |
| 8YSZ | - | - | 12.7 | 4.56 | 97.0% | [117] |
| 8YSZ | CNTs | 2.6 vol% | 11.6 | 6.44 | 97.3% | [117] |
| 8YSZ | CNTs | 7.6 vol% | 10.8 | 8.63 | 97.5% | [117] |
| 3Y-TZP | - | - | 14.21 ± 0.09 | 3.57 ± 0.01 | 99.4 ± 0.2% | [118] |
| 3Y-TZP | MWCNTs | 0.5 wt% | 12.98 ± 0.08 | 4.02 ± 0.01 | 98.8 ± 0.3% | [118] |
| 3Y-TZP | MWCNTs | 2 wt% | 9.52 ± 0.05 | 4.97 ± 0.06 | 96.6 ± 0.2% | [118] |
| 8YSZ | - | - | 13.52 ± 0.40 | 5.21 ± 0.20 | 5.83 g/cm3 | [123] |
| 8YSZ | MWCNTs | 1 wt% | 12.96 ± 0.30 | 6.58 ± 0.30 | 6.23 g/cm3 | [123] |
| ZTA | - | - | 18.75 ± 0.27 | 5.64 ± 0.23 | 99.62 ± 0.07% | [127] |
| ZTA | MWCNTs | 0.01 wt% | 19.13 ± 0.25 | 4.18 ± 0.43 | 99.58 ± 0.02% | [127] |
| ZTA | MWCNTs | 0.1 wt% | 19.39 ± 0.15 | 5.21 ± 0.22 | 98.91 ± 0.03% | [127] |
| 8YZ | - | - | ~10.5 GPa | ~2.0 | 99.9% | [128] |
| 8YZ | CNTs | 1 wt% | ~11.0 GPa | ~3.5 | 99.9% | [128] |
| 8YSZ-Al2O3 | - | - | 11.09 ± 4.10 | 1.48 ± 0.68 | 94.3% | [129] |
| 8YSZ-Al2O3 | CNTs | 3 wt% | 16.47 ± 5.10 | 1.76 ± 0.65 | 98.5% | [129] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lamnini, S.; Pugliese, D.; Baino, F. Zirconia-Based Ceramics Reinforced by Carbon Nanotubes: A Review with Emphasis on Mechanical Properties. Ceramics 2023, 6, 1705-1734. https://doi.org/10.3390/ceramics6030105
Lamnini S, Pugliese D, Baino F. Zirconia-Based Ceramics Reinforced by Carbon Nanotubes: A Review with Emphasis on Mechanical Properties. Ceramics. 2023; 6(3):1705-1734. https://doi.org/10.3390/ceramics6030105
Chicago/Turabian StyleLamnini, Soukaina, Diego Pugliese, and Francesco Baino. 2023. "Zirconia-Based Ceramics Reinforced by Carbon Nanotubes: A Review with Emphasis on Mechanical Properties" Ceramics 6, no. 3: 1705-1734. https://doi.org/10.3390/ceramics6030105
APA StyleLamnini, S., Pugliese, D., & Baino, F. (2023). Zirconia-Based Ceramics Reinforced by Carbon Nanotubes: A Review with Emphasis on Mechanical Properties. Ceramics, 6(3), 1705-1734. https://doi.org/10.3390/ceramics6030105