Low-Momentum Pion Enhancement from Schematic Hadronization of a Gluon-Saturated Initial State
Abstract
:1. Introduction
2. Kinetic Equation Approach to Thermalization and Hadronization
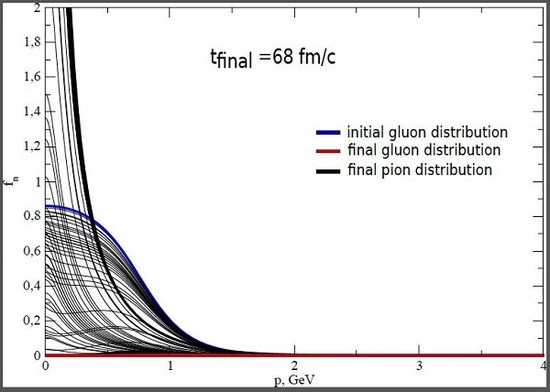
3. Results
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Collision Integral Derivation
References
- Abelev, B.B.; Adam, J.; Adamová, D.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agocs, A.G.; Agostinelli, A.; Agrawal, N.; Ahammed, Z.; et al. Two- and three-pion quantum statistics correlations in Pb-Pb collisions at = 2.76 TeV at the CERN Large Hadron Collider. Phys. Rev. C 2014, 89, 024911. [Google Scholar] [CrossRef]
- Kataja, M.; Ruuskanen, P.V. Nonzero Chemical Potential and the Shape of the pT Distribution of Hadrons in Heavy Ion Collisions. Phys. Lett. B 1990, 243, 181–184. [Google Scholar] [CrossRef]
- Gavin, S.; Ruuskanen, P.V. Low p(T) pion enhancement from partial thermalization in nuclear collisions. Phys. Lett. B 1991, 262, 326–332. [Google Scholar] [CrossRef]
- Begun, V. Thermal model for Pb+Pb collisions at = 2.76 TeV with explicit treatment of hadronic ground states. EPJ Web Conf. 2015, 97, 00003. [Google Scholar] [CrossRef]
- Begun, V.; Florkowski, W.; Rybczynski, M. Transverse-momentum spectra of strange particles produced in Pb+Pb collisions at = 2.76 TeV in the chemical non-equilibrium model. Phys. Rev. C 2014, 90, 054912. [Google Scholar] [CrossRef]
- Begun, V.; Florkowski, W.; Rybczynski, M. Explanation of hadron transverse-momentum spectra in heavy-ion collisions at = 2.76 TeV within chemical non-equilibrium statistical hadronization model. Phys. Rev. C 2014, 90, 014906. [Google Scholar] [CrossRef]
- Blaizot, J.P.; Gelis, F.; Liao, J.F.; McLerran, L.; Venugopalan, R. Bose–Einstein Condensation and Thermalization of the Quark Gluon Plasma. Nucl. Phys. A 2012, 873, 68–80. [Google Scholar] [CrossRef]
- Begun, V.V. High temperature Bose-Einstein condensation. EPJ Web Conf. 2016, 126, 03002. [Google Scholar] [CrossRef] [Green Version]
- Begun, V.; Florkowski, W. Bose-Einstein condensation of pions in heavy-ion collisions at the CERN Large Hadron Collider (LHC) energies. Phys. Rev. C 2015, 91, 054909. [Google Scholar] [CrossRef]
- Voskresensky, D.N. Kinetic description of a pion gas in ultrarelativistic collisions of nuclei: Turbulence and Bose condensation. Phys. Atom. Nucl. 1996, 59, 2015–2023. [Google Scholar]
- Semikoz, D.V.; Tkachev, I.I. Condensation of bosons in kinetic regime. Phys. Rev. D 1997, 55, 489–502. [Google Scholar] [CrossRef]
- Voskresensky, D.N.; Blaschke, D.; Roepke, G.; Schulz, H. Nonequilibrium approach to dense hadronic matter. Int. J. Mod. Phys. E 1995, 4, 1–45. [Google Scholar] [CrossRef]
- Koch, P.; Rafelski, J. Why the Hadronic Gas Description of Hadronic Reactions Works: The Example of Strange Hadrons. S. Afr. J. Phys. 1986, 9, 8–23. [Google Scholar]
- Stoecker, H.; Zhou, K.; Schramm, S.; Senzel, F.; Greiner, C.; Beitel, M.; Gallmeister, K.; Gorenstein, M.; Mishustin, I.; Vasak, D.; et al. Glueballs amass at RHIC and LHC Colliders!—The early quarkless 1st order phase transition at T = 270 MeV—From pure Yang-Mills glue plasma to GlueBall-Hagedorn states. J. Phys. G 2016, 43, 015105. [Google Scholar] [CrossRef]
- Blaizot, J.P.; Liao, J.; McLerran, L. Gluon Transport Equation in the Small Angle Approximation and the Onset of Bose-Einstein Condensation. Nucl. Phys. A 2013, 920, 58–77. [Google Scholar] [CrossRef]
- Blaizot, J.P.; Jiang, Y.; Liao, J. Gluon transport equation with effective mass and dynamical onset of Bose–Einstein condensation. Nucl. Phys. A 2016, 949, 48–70. [Google Scholar] [CrossRef] [Green Version]
- Rehberg, P.; Bot, L.; Aichelin, J. Expansion and hadronization of a chirally symmetric quark-meson plasma. Nucl. Phys. A 1999, 653, 415–435. [Google Scholar] [CrossRef] [Green Version]
- Rehberg, P.; Klevansky, S.P.; Hufner, J. Hadronization in the SU(3) Nambu-Jona-Lasinio model. Phys. Rev. C 1996, 53, 410–429. [Google Scholar] [CrossRef]
- Friesen, A.V.; Kalinovsky, Y.V.; Toneev, V.D. Quark scattering off quarks and hadrons. Nucl. Phys. A 2014, 923, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Marty, R.; Torres-Rincon, J.M.; Bratkovskaya, E.; Aichelin, J. Transport Theory from the Nambu-Jona-Lasinio Lagrangian. J. Phys. Conf. Ser. 2016, 668, 012001. [Google Scholar] [CrossRef] [Green Version]
- Feng, B.; Xu, Z.; Greiner, C. Dynamical scheme for hadronization with first-order phase transition. Phys. Rev. C 2017, 95, 024907. [Google Scholar] [CrossRef]
- Florkowski, W.; Maksymiuk, E.; Ryblewski, R.; Tinti, L. Anisotropic hydrodynamics for a mixture of quark and gluon fluids. Phys. Rev. C 2015, 92, 054912. [Google Scholar] [CrossRef]
- Florkowski, W.; Ryblewski, R.; Su, N.; Tywoniuk, K. Bulk viscosity in a plasma of Gribov-Zwanziger gluons. Acta Phys. Pol. B 2016, 47, 1833. [Google Scholar] [CrossRef]
- Florkowski, W.; Ryblewski, R.; Su, N.; Tywoniuk, K. Strong-coupling effects in a plasma of confining gluons. Nucl. Phys. A 2016, 956, 669–672. [Google Scholar] [CrossRef] [Green Version]
- Shuryak, E.V. Two stage equilibration in high-energy heavy ion collisions. Phys. Rev. Lett. 1992, 68, 3270–3272. [Google Scholar] [CrossRef] [PubMed]
- Zhou, K.; Xu, Z.; Zhuang, P.; Greiner, C. Kinetic description of Bose-Einstein condensation with test particle simulations. Phys. Rev. D 2017, 96, 014020. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.; Zhou, K.; Zhuang, P.; Greiner, C. Thermalization of gluons with Bose-Einstein condensation. Phys. Rev. Lett. 2015, 114, 182301. [Google Scholar] [CrossRef] [PubMed]
- Andronic, A.; Braun-Munzinger, P.; Redlich, K.; Stachel, J. Decoding the phase structure of QCD via particle production at high energy. Nature 2018, 561, 321–330. [Google Scholar] [CrossRef] [PubMed]
- Seifert, E.; Cassing, W. Baryon-antibaryon annihilation and reproduction in relativistic heavy-ion collisions. Phys. Rev. C 2018, 97, 024913. [Google Scholar] [CrossRef]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nazarova, E.; Juchnowski, Ł.; Blaschke, D.; Fischer, T. Low-Momentum Pion Enhancement from Schematic Hadronization of a Gluon-Saturated Initial State. Particles 2019, 2, 140-149. https://doi.org/10.3390/particles2010010
Nazarova E, Juchnowski Ł, Blaschke D, Fischer T. Low-Momentum Pion Enhancement from Schematic Hadronization of a Gluon-Saturated Initial State. Particles. 2019; 2(1):140-149. https://doi.org/10.3390/particles2010010
Chicago/Turabian StyleNazarova, Elizaveta, Łukasz Juchnowski, David Blaschke, and Tobias Fischer. 2019. "Low-Momentum Pion Enhancement from Schematic Hadronization of a Gluon-Saturated Initial State" Particles 2, no. 1: 140-149. https://doi.org/10.3390/particles2010010
APA StyleNazarova, E., Juchnowski, Ł., Blaschke, D., & Fischer, T. (2019). Low-Momentum Pion Enhancement from Schematic Hadronization of a Gluon-Saturated Initial State. Particles, 2(1), 140-149. https://doi.org/10.3390/particles2010010