1. Introduction
Suppose that a structure is responsive to electromagnetic (EM) waves. When there is a temperature variation in the medium surrounding that structure, that structure undergoes conformational alterations. Such temperature-induced alterations of the EM responses constitute the main topic of this review. In a rare case, the EM waves could be altered by structural changes as well.
The above statements need further clarification. Firstly, a structure under consideration can be made of various kinds of materials. Secondly, a surrounding medium can be gas, liquid, solid, etc. Thirdly, the range of temperature variations in view of the material properties of a structure determines how severe the resulting temperature sensitivity of a structure is. Fourthly, temperature variations during or after the fabrication of a structure need to be handled in different ways.
Lastly, the characteristic sizes of both structure and surrounding medium in comparison to the typical wavelength of EM waves determine the ways of theoretical analysis and numerical analysis. For instance, nano-scale structures will be most interesting to visible lights, while centimeter-scale structures would be sufficient in considering their responses to radio waves. For concreteness, we are restricted to EM waves over visible lights to microwaves so that the characteristic sizes of the structures under this review are less than one millimeter, for instance [
1,
2,
3]. This size restriction assures that effective-medium theory is applicable [
4].
Conventionally, ‘chiral’ is a geometric notion indicating ‘non-mirror symmetric’ [
5]. For this reason, ‘helical’ refers to ‘geometry (conformation)’ in this review, while ‘chiral’ is associated with ‘(optical) property’. However, ‘chirality’ sometimes stands for a mere ‘geometric chirality’ without any associated physical features [
6,
7]. Nature provides us with ample examples of chirality in the fields of biology, chemistry, physics, mathematics, and minerals [
8].
Figure 1 illustrates several configurations made from hollow shells of cylindrical cross-sections. In
Figure 1a, the mesh lines and curves indicate undeformed materials. In comparison, the vertical mesh lines in
Figure 1a are deformed into curved ones in
Figure 1b due to the sidewise compression and decompression, as indicated by the horizontal blue arrows in
Figure 1b. This configuration is also established as a breathing mode on resonance.
Figure 1b shows, hence, a breathing mode [
9].
Figure 1c exhibits a helix that is deformed from
Figure 1a by an applied torque couple, as indicated by the pair of semi-circular red arrows on both the top and bottom ends. Here in
Figure 1c, the upper torque vector is directed upward along the cylindrical axis, whereas the lower torque vector is directed downward along the cylindrical axis. Details in
Figure 1 will be discussed later.
Oftentimes, ‘unidirectional’ and ‘chiral’ are interchangeably employed in describing one-way motions or information transfer [
10,
11]. The bi-characteristic curves associated with the two distinct refractive indices are suitable for handling bipartite quantum states [
12]. Such chiral quantum mechanics shares analogous formulations with what are discussed here for chiral media. The purpose of this review is to identify the thermal effects on chiral media and further on EM chirality. Both chiral molecules dispersed in fluids and artificial chiral meta-atoms imbedded in solids are affected by variations in temperature. Key idea of this article is to examine how temperature variations cause structural changes in the chiral molecules and artificial chiral meta-atoms. To this goal, relationships among phonons and electrons will be examined in connection with temperature variations.
The term ‘chiral’ in this paper refers to the properties of electromagnetic waves. The term ‘handed’ is synonymous to ‘chiral’, the latter being more often employed in this paper. The term ‘helical’ is employed predominantly for geometrical shapes in this paper, although ‘helical’ and ‘chiral’ are interchangeably employed in many of other referenced papers.
This review is structured in the following way.
Section 2 examines light–matter interactions in various facets while emphasizing electric, magnetic, and magnetoelectric matters.
Section 3 summarizes typical constitutive relations for chiral media as employed for the Maxwell equations.
Section 4 handles the mechanics of chiral objects in connection with thermal effects. Here, temperature-mediated electron–phonon interactions are illustrated.
Section 5 examines Ogema particles, either twisted or untwisted, as meta-atoms that constitute chiral media.
Section 6 takes flat fishes as an example to show various aspects of chirality.
Section 7 presents other chiral meta-atoms as regards temperature-mediated electron–phonon interactions.
Section 8 offers discussions, followed by conclusions in
Section 9.
2. Light–Matter Interactions
As a generalization of light–matter interactions, consider field–matter interactions illustrated in
Figure 2. Notice that jargon employed in continuum mechanics and that for quantum mechanics are mixed up without too much rigor. For the sake of our study, the fields (in the outer rectangular light-yellow domain) in
Figure 2 are classified into temperature field, acoustic field (stress field or phonons), electric field, magnetic field, and EM field. Meanwhile, matters (in the inner rectangular light-blue domain in
Figure 2 are grouped into dielectric (non-electric and non-magnetic), electric matter, magnetic matter, magnetoelectric matter [
13].
A magnetoelectric matter contains simultaneous features both of electric matter and magnetic matter. Sharp delineations of fields and matters presented in
Figure 2 are made just for convenience since they may cause controversy from rigorous viewpoints. In the forthcoming sections, we will specialize those materials further into metals, semiconductors, dielectrics, magnetic materials [
13,
14], polymers [
15], liquid crystals [
5,
16], etc.
As sketched in
Figure 2, the light–matter interactions between EM waves and a chiral media involve diverse phenomena involving photons, phonons, electrons, etc. Both random thermal fluctuations and imposed thermal gradients will play competing influences on light–matter interactions [
17]. In this connection, multiple length and time scales should be taken into consideration [
14] (pp. 287–322). Meta-atoms being of a typical length scale much shorter than the typical wavelength of EM waves is the fundamental assumption underlying the effective-medium theory [
4].
Let us loosely define the Bose factor as follows.
Here, are a certain energy, a compatible chemical potential, the Boltzmann constant, and temperature, respectively. Hence, the Bose factor B increases with T, while decreasing with E. For a simple case that with as the reduced Planck constant and frequency, we obtain the second formula in Equation (1).
Consider elasticity (phonon dynamics) indicated by (a) in
Figure 2, where interactions between phonons within matters and acoustic (stress) fields take place. For phonons as bosons, the temperature dependence shows itself up through the above Bose factor provided in Equation (1). Thermo-acoustic effects are marked by item (b) in
Figure 2, among which temperature-dependent refractive indices make one example [
18].
The item ‘dielectrics’ listed as one of the ‘matters’ in
Figure 2 refers to matters that are neither electrically nor magnetically polarizable. Dielectrics include, say, vacuum, air (approximately), and normal glasses. Electric matters refer here, say, to non-magnetic metals such as gold, silver, and copper. Consider the situation with the Landau quantization as marked by item (c) in
Figure 2, where applied electric and magnetic fields influence an electrically conducting strip. The Landau quantization is characterized by a transverse electric current that is established from interactions between the magnetic field and electric matter. Normally, thermal effects are not taken into consideration for the Landau quantization.
Temperature gradients are key players not only for the thermoelectric Seebeck effect but also for the magnetic Seebeck effect, as stated in [
14] (pp. 1–23, 357–404) and [
19]. A topological magnetic Hall effect is associated with unidirectional (chiral) motions of skyrmions depending on the signs of participating magnons [
19]. Moreover, stochastic thermal fluctuations are normally taken into consideration for magnetic Seebeck effects [
19].
It is seen from the Landau–Lifshitz equation for the magnetic order parameter that the spatial gradients of the magnetization (as a material property) are crucial for the proper workings of chiral magnets [
20]. Such magnetization gradients could arise from thermal gradients. In this respect, it is both surprising and counterintuitive that skyrmion motions are executed toward a thermal source (i.e., toward a higher-temperature region) [
20]. The skyrmion caloritronics is concerned with thermal spin transport for a dilute gas of skyrmions in clean insulating chiral magnets [
20]. The pertinent skyrmion dynamics can be considered as a magnetic counterpart of the Landau quantization sketched as item (c) in
Figure 2.
Magnetic spin textures are categorized into various geometric configurations in Figure 14.1 of [
14] (pp. 357–404): zero-dimensional (0D), one-dimensional (1D), two-dimensional (2D), and three-dimensional (3D). Such dimensionality issues are related to how meta-atoms are fabricated, as will be briefly summarized in our forthcoming Tables.
As illustrated by item (d) in
Figure 2, couplings among two Kittel modes and one film magnon are examined in [
14] (pp. 1–23). Refer also to [
3]. Mechanical deformations (phonons) and attendant thermal effects have been taken into consideration for magnetic materials [
3,
17] and other matters [
2]. Magnon–cavity coupling is essential to proper interactions between photons within a cavity composed of oxygen-free copper and magnetic spins of a ferrimagnetic YIG sphere [
3]. Moreover, the Kittel linewidth exhibits a minimum feature with respect to varying temperature.
As illustrated as interactions among EM field, electric matter, and dielectric by item (e) in
Figure 2, surface plasmon waves are established between a metal and a dielectric medium. Optical losses would then lead to thermal effects that might influence, in turn, the metals’ optical performance.
As marked by item (f) in
Figure 2, surface plasmon waves are established between a metal and a chiral medium [
21,
22,
23,
24], for which details of the dispersed chiral objects are not revealed. The resulting ‘chiral surface plasmon resonance (CHISPR)’, as coined by [
14] (pp. 25–52), stands for interactions among EM fields, magnetoelectric matters (say, a chiral medium), and an electric matter (a metal). Both geometric configuration and stereochemical structures of chiral objects determine their response to applied fields [
25,
26,
27]. Chiral media containing magnetic chiral objects could also lead to plasmonic resonances. See [
14] (pp. 53–74) and [
28].
3. Chiral Media and Constitutive Relations
Chirality is associated with two additional features [
29,
30]. Firstly, chirality manifests itself through a rotation of the polarization plane of EM waves propagating through a chiral medium. The polarization rotation is alternatively termed ‘optical rotatory dispersion (ORD)’ [
6,
14,
31,
32,
33]. Secondly, chirality is largely accompanied by magnetoelectric coupling [
14,
32,
34,
35,
36]. Both optical rotatory dispersion and magnetoelectric coupling are mostly (but not always) associated with spin–orbit coupling (SOC) [
10,
34,
37,
38,
39].
Of course, both ORD and magnetoelectric coupling could also be established in achiral media. As an example, magnetic media could induce magnetic circular dichroism, as seen with Faraday rotation [
28,
38]. As a relevant issue, a transverse electric (TE) wave and a transverse-magnetic (TM) wave are often considered fundamental solutions to linear electromagnetic waves [
39,
40,
41]. The aforementioned SOC often (albeit not always) comes together with a TM–TE coupling, as seen for the CHISPR in [
22,
23].
Table 1 shows two types of matters: soft matters and condensed matters.
Chiral media are enjoying renewed interest in optics. The reason lies in the availability of chiral objects obtainable by various nanofabrication techniques [
6,
21,
50].
Table 1 provides a summary of two types of chiral media: (i) chiral media, for example, fluid is uniformly dispersed by an ensemble of chiral objects, and (ii) chiral metamaterials, for example, solid media periodically embedded with chiral objects of artificial meta-atoms.
Table 1 contains schematic illustrations for comparison.
The ‘
electromagnetic (EM) chirality’ is constructed from both
and
, where
are electric and magnetic field vectors. See [
14] (pp. 75–103) and [
29,
51]. Oftentimes, ‘EM chirality’ is alternatively and confusingly called a ‘light helicity’ [
21]. For the forthcoming symbols, we employ the overbar ‘-’ to denote dimensional variables and parameters. In comparison, symbols without an overbar are dimensionless. Consider the following set of Maxwell equations.
Here, are electric displacement and magnetic flux density, whereas are the dimensionless electric permittivity and magnetic permeability, respectively. Furthermore, is the light speed in vacuum, and , where is a certain prescribed frequency. The gradient operator is correspondingly made dimensionless such that .
In addition, either of the following pairs of constitutive relations (CRs) is employed.
Equations (2) and (3) take dimensionless forms, for which the scheme of making various variables and parameters is detailed in [
39]. The dimensional chirality parameters
are related to the dimensionless chirality parameters
through the respective relations
and
. The CRs of Equation (3) are valid for chiral media with various dispersed building blocks. In the case with fluids randomly dispersed with chiral objects, both of
are roughly proportional to the relative volume of the immersed chiral objects [
35,
47].
The Tellegen parameter
represents material loss of chiral objects [
24]. The case with
is conducive to circular dichroism (CD) with differential absorptions [
21,
29,
44,
45]. We will henceforth set
for simplicity so that both of
are assumed real. By effective-medium theory [
4], angular averaging is taken for orientationally ordered chiral objects [
21,
32,
52]. For metamaterials that contain positionally ordered meta-atoms, such an isotropy would not hold true.
Quantum-mechanical formulas for
are constructed based on oscillator models for a two-level system with linear perturbations [
32]. Here, the Born–Kuhn model for coupled oscillators is employed for the dynamics of two oscillators in interactions with EM waves of two circular polarizations [
6,
17,
32].
Table 2 compares two types of constitutive relations for chiral media.
The first pair
is called the ‘Pasteur’ CRs, whereas the second pair
is called the ‘Drude–Born–Fedorov (DBF)’ CRs. Both
refer to bi-anisotropic chiral media, respectively, with single chirality parameters
[
40]. To the leading order in small values of
, namely, for
, both of
are approximately equivalent [
26]. Comparative features of
are summarized in
Table 2, together with pertinent references. In the meantime,
is alternatively dubbed a ‘chiral admittance’ [
27,
56] while being proportional to the anisotropy factor [
32].
CRs are alternatively called ‘material connections’ [
32]. Moreover, optically active liquids (say, octyl alcohol, limonene, ethyl tartrate, etc.) consisting homogeneously of chiral molecules are investigated to show the dependence of
on several parameters: the density of liquid, the number densities of chiral constituent molecules, electric and magnetic polarizabilities of molecules, quantum-transition probabilities, etc. [
32]. In addition, a more sophisticated pair of CRs is presented in [
32] such that it adds transient (time-dependent) terms to the instantaneous forms given in Equation (3). See [
52].
Chiral media carry bi-anisotropic responses to EM fields, where the effective refractive indices are given, respectively, as follows [
25,
32,
47,
50,
55,
58].
Of course, we obtain the effective refractive index
for achiral cases with
. For larger chirality parameter with
or
, negative refractive index could be obtained [
25,
26,
29,
36,
45,
50]. An extended version of
is presented in the name of spatial–spectral CRs by [
29]. In addition, both of
are frequency-dispersive in general [
6,
21,
31,
32,
33].
The Pasteur CRs
carry only local terms involving
. In comparison, nonlocal portions
with spatial derivatives are seen in
[
29,
52]. Hence,
lends itself to simpler interpretation than
. Moreover, a pseudoscalar property of
is evident, whereas pseudoscalar property of
is less clear. See [
32] and [
59] (p. 243).
The controversy as to whether CRs contain spatial derivatives or not is also encountered in fluid dynamics. For instance, Korteweg-type CRs include not only standard fluid-dynamic variables but also the density gradient in the context of Korteweg tensor [
60,
61]. Instead of the local Newtonian stresses, capillary forces in fluids are more adequately accounted for by the Korteweg stresses, where temperature dependence of capillarity can be incorporated. In this respect, the Korteweg-type CRs are based on an extended version of nonequilibrium thermodynamics. Those Korteweg-like CRs are derived using the second gradient theory [
62], where the concepts like multipolarity or interstitial dynamics have been resorted to.
Notice that capillary flows invariably involve non-planar spatial domains, from which we expect complicated geometrical configurations of chiral embedded objects to be better represented by
. Both flows of compressible fluids discussed in [
60,
61] and the EM waves propagating through chiral media are accompanied by bi-characteristics provided by Equation (4). It remains for us to see whether the curl-based DBF CRs
better describe the multipolar electrodynamics and the magnetoelectric coupling hidden under the light–matter interactions occurring through chiral media [
32].
In concrete examples for the propagations of EM waves through chiral media with appropriate boundary conditions, it is found that more problems are solved with
[
22,
23], while less problems are solved with
as listed in
Table 2. Therefore, we are focusing oftentimes on
in this review for convenience.
A usefulness of chirality parameter
can be seen by supposing a liquid that is homogeneously dispersed by a random ensemble of chiral molecules. In this case, the rotation angle
of the polarization plane of EM waves propagating through a distance
is given as follows.
See [
14] (pp. 25–52) and [
15,
32]. Here, the subscript ‘ORD’ stands for the aforementioned ‘optical rotatory dispersion (ORD)’. The ‘optical rotation (OR)’ angle also refers to Equation (5). See also [
30]. Normally, only the frequency dependence
is reported by [
45], thus leaving us with another difficult task of finding geometric dependence
. For large chirality parameters, nonlinear analyses might be necessary [
52].
Plasma flows under externally applied magnetic fields constitute effective chiral media that are adequately described by the Pasteur CRs [
54]. Let the parameter
denote the electron cyclotron frequency of an applied external magnetic field [
54]. In this case, the effective chirality parameter
is proportional to
, whence the sign of
depends on the difference
. Moreover,
is odd in
. Moreover, the TM–TE coupling is clearly seen from the solutions in [
54].
In the meantime, higher-order DBF CRs have been proposed in [
40,
41], where the following CRs are employed.
Here, and are higher-order chirality parameters, being tensors of appropriate ranks. Even higher-order DBF CRs can be readily envisaged.
In addition, spatially heterogenous media pose difficulties for the DBF CRs, since
and
in Equation (3) for a charge-free space demand
and
, respectively [
56].
4. Mechanics and Thermal Effects of Chiral Objects
Suppose that either mechanical forces or thermal effects cause mechanical deformations of structures. Consider a cylindrical column of finite length, as depicted in
Figure 3. Here, the Poisson ratio (
) is defined to be the negative of a lateral (radial) strain to a longitudinal (axial) strain. See [
14] (pp. 287–322) and [
63,
64].
Both
Figure 3a–c are obtained for positive Poisson ratios, viz.,
. Consider
Figure 3a first. Under compression in the axial longitudinal direction, the lateral diameter is enlarged in compensation for the axial shortening. Consider
Figure 3c second. Under decompression in the axial longitudinal direction, the lateral diameter is shortened in compensation for the axial elongation (or prolongation) [
7,
65]. As depicted in
Figure 3d–f, opposite changes in the length and diameter take place for the Poisson ratio being negative, viz.,
.
By the volume conservation of a homogeneous hard material, it is required for isotropic linear elastic materials that
for 3D structures and
for 2D structures [
66]. For continuous solids, the apparent Poisson ratio is proportional to the atomic packing density (APD) of the constituent molecules for crystalline metals. From a simple reasoning, the higher the APD the harder a given material becomes. Harder materials resist lateral deformation for a given longitudinal deformation. Therefore, the Poisson ratio becomes smaller with increasing APD.
Soft matters such as DNAs are endowed with larger values of
, while hard matters such as concretes are equipped with smaller values of
. Meanwhile, the Poisson ratios of metals are relatively large. For instance,
for copper, and
for gold. Periodic structures could exhibit effective negative Poisson ratios [
67,
68]. For instance, a certain foam exhibits
, as seen with 2D chiral honeycombs [
67]. Notice that such honeycomb media can be considered composite media. Depending on specific materials, negative Poisson ratios may lead to unexpected chirality parameters. A hierarchical achiral 2D metastructure could turn into a hierarchical chiral 2D metastructure under either compression or elongation [
68].
It is reported in [
66] that
for an anisotropic polytetrafluoroethylene (PTFE) in a true strain range of 0.03. From the viewpoint of stereochemistry, this anisotropic PTFE consists of chains of atoms and bonding members. In the case with a metamaterial consisting of periodically folded sheets (say, either Origami or Miura-ori), an effective Poisson ratio ranging over
is reported [
69]. In such mechanical anisotropic metamaterials, the effective Poisson ratio is altered depending on the direction of applied force. Thermosetting polymer foams stand for temperature effects during fabrication.
In the case of subwavelength small nanoparticles (NPs), the surface plasmon resonance can be gradually tuned via prolongation of the NP along one axis covering the whole visible and near-infrared (IR) region [
2]. Such non-spherical matters are endowed with nonzero Poisson ratios. In this aspect, magnetoelastic waves are analyzed in [
14] (pp. 287–322).
In the meantime, the expansion–contraction scenarios within a solid as illustrated in
Figure 3 could take place during a short transient process in fabricating nanoparticles by intense ion-beam irradiations [
63], where thermal stresses influence the deformation processes as well. In this regard, viscous and plastic deformations could also take place [
64] for thermally grown nanostructures during a fast transient period involving strong ion-beam irradiation fluxes.
For a given mass of a meta-atom, its volume varies with temperature on which the Poisson ratio depends [
70]. In addition, the Poisson ratio could depend on the loading history for viscoelastic materials [
70]. For instance, crystalline metals exhibit
[
65,
66,
71]. For metals with higher electrical conductivities, the Poisson ratios are also higher in general, thus indicating an increased malleability and electron–phonon interactions. Especially for rubbery materials, the Poisson ratio experiences a sharp increase as the temperature is increased across its glass temperature, viz.,
[
66]. In contrast, it could happen that
with some other materials. Such a temperature dependence of the Poisson ratio stems from the connectivity variations in glasses and liquids.
For certain media, there could exist a special temperature
for a vanishing Poisson ratio, namely,
. In this connection, the apparent Poisson ratio of a whole chiral medium should depend on the concentration of the dispersed chiral objects [
66]. As a relevant example, a temperature-dependent inversion in the chirality parameter takes place with the homogeneous chiral liquid of ethyl tartrate [
32]. In brief,
Consider the electron transports through non-centrosymmetric Weyl semimetals [
72,
73,
74], which are characterized by strong SOCs among electrons. The magnetization of such chiral crystals is accompanied by a damping factor. This damping factor carries the Lifshitz–Kosevich dependence
[
72]. Here,
, where
,
, and
are effective mass, temperature, and applied magnetic field. Therefore, smaller effective mass, lower temperature, and larger applied magnetic field are all conducive to a constant limit form
as
. Those chiral anomalies manifest themselves also through strain-induced electron transport [
74].
Let us examine basic dynamical modes of a thin tube composed of a single elastic material [
75]. Regarding
Figure 1a, suppose that deformations in linear elasticity follow
, where
are cylindrical coordinates. The three lowest dynamic vibrational modes of finite-length cylindrical shells are discussed in [
75]. We find a radial breathing mode (RBM) for
as depicted on the previous
Figure 1b. In the case with skyrmion lattices, we find two gyration modes in addition to a single breathing mode [
20]. This ‘achiral’ RBM plays a key role in the near-field Raman spectroscopy in extracting structural information of the chiral carbon nanotubes [
76], where a pair of integers determines the geometric chirality.
In comparison, a helix mode is established for
, while an ovalization mode prevails for
. Therefore, nonzero chirality is established for
for cylindrical structures. In addition, boundary conditions could select which modes to prevail with time as seen from
Figure 1b,c. It is important to design a whole elastic system both by selecting proper materials and by imposing necessary boundary conditions. Temperature effects would increase with increasing
.
Figure 1e illustrates an ovalization mode for a solid cylinder, where an applied torque couple is indicated by the pair of semi-circular green arrows. Here in
Figure 1e, both torque vectors are directed out of the page. Because of this torque couple (viz., bending moments), the cross-section becomes elliptical from a circular one, as indicated by
Figure 1f. Such a cross-sectional ovalization arises from the transverse mode instability [
77], which can also be thermally induced. Meanwhile, the buckling stress under compression estimated from elasticity theory breaks down as
[
78].
What will happen to a cylinder of negative Poisson ratio when such bending moments are applied? When the cylindrical material becomes sufficiently soft and temperature sensitive, we would have a non-negligible opto-mechanical coupling over the frequency range far below that of the visible light [
76]. Such opto-mechanical coupling would become more probable if higher-order (namely, with a larger
) ovalization modes are resonantly excited.
Consider a waveguide composed of silicon oxynitride [
18], where an effective refractive index
can be evaluated [
25]. The resulting thermo-optic coefficient
obtained in the setting of a waveguide shows a strong temperature dependence [
18]. It remains to verify the easy manufacturability of dielectric materials into chiral meta-atoms. During fabrication, an additional issue of residual stresses should be taken care of. An analogous effect plays a key role in realizing thermally induced refractive-index gratings in Yb-doped fibers [
77].
For modulation purposes, a dielectric elastomer can be actuated by applied electric potential so that even a necking phenomenon might take place based on a positive Poisson ratio, as illustrated in Figure 1 of [
79]. Through careful fabrication, a multilayer stack of helical structures can also be realized, as depicted in Figure 11 of [
79] and on various figures of [
80]. Such stacked configurations offer easier contractibility along its longitudinal axis. Energy conversion between electric energy and elastic energy underlies the operation of such an electroactive elastomer [
79]. Furthermore, helical stacked multilayer configurations provide us with electrically contractile monolithic actuators when alternating flexible electrodes are interposed [
80]. It remains to be seen how to further miniaturize those electroactive polymers employed in [
80] for the purpose of being employed as EM meta-atoms.
Optical materials exhibiting phase transitions upon temperature variations are employed for optical switches and modulators [
65]. For instance, vanadium dioxides (
) undergo phase transitions between metallic and insulating states due to temperature variations, which are caused, in turn, by externally applied electric potentials [
81]. As an electro-optic material,
[
81] possesses high refractive indices, which also increase with decreasing wavelength [
82].
carries both a metal-insulator transition and a structural phase transition owing to electron–phonon interactions [
83]. Moreover, both electron correlations and lattice distortions of
are known to be dependent on temperature [
83]. Under compression, the critical stress necessary for a certain structural phase transition depends on the critical temperature as given by Equation (1) of [
83].
In optical devices based on
should be designed by taking the lateral Poisson ratio effects if typical feature sizes of a device are on the order of optical wavelengths. In this regard, it is stated in [
66] that scientists from many different fields still ignore the variability of Poisson’s ratio as observed, for instance, with viscoelastic materials.
In the case with a thin film of vanadium pentoxide (
) [
84], the optical transmission exhibits a maximum feature at a certain wavelength, while it decreases largely with increasing temperature. The photoluminescence intensity also increases largely with decreasing temperature [
84] due to thermal lattice dilatations and electron–phonon interactions. In general, phase transitions are thought to be caused by lattice distortions (Peierls) and/or electron correlations (Mott) [
83].
Figure 4 illustrates the interactions between electrons and phonons at two distinct temperatures.
Figure 4(a1,b1) illustrate side views of a pan, whereas
Figure 4(a2,b2) show top views of a pan of (intentionally) non-circular cross-section. The colored disks in
Figure 4(a1,a2,b1,b2) over the surface of the respective pans emulate electrons. In comparison, the ice-covered waters in
Figure 4(a1,a2) and the water masses in
Figure 4(b1,b2) emulate phonons, respectively.
Figure 4a displays a pan with disks obtained at a lower temperature. The corresponding top view in
Figure 4(a2) shows three disks. Here, the upper left blue disk follows a straight path as indicated by ‘A’, while the lower left blue disk follows a mildly curved trajectory ‘B’ to reach the right-disk position. The curved path ‘B’ is especially intended to signify a certain path along the edge (namely, the boundary of a pan).
In comparison,
Figure 4b depicts a water-filled pan with disks obtained at a higher temperature. The top view in
Figure 4(b2) shows three disks. Here, both left blue disks may follow relatively random paths to reach the right-disk position. Therefore, we hardly find a trajectory aligned along the edge (namely, the boundary of a pond).
The preceding illustrative comparison is intended to show key distinctions of the electron–phonon interactions at varied temperatures.
Figure 4a may also illustrate what occurs to electron–phonon interactions at extremely low temperatures (i.e., low-temperature superconductors). In addition, thermal fluctuations play nontrivial roles in making estimates of stresses and strains in finite-sized nanostructures [
65]. In this case, soft maters and hard matters require different approaches based on the distinction between the Gibbs ensemble (soft devices) and the Helmholtz ensemble (hard devices) [
65].
It is instructive to consider flow fields through the inside of a solid tube [
85]. A laminar Poiseuille flow is normally established when a mean axial flow speed is sufficiently low. If a thin twisted tape is inserted into the inside of a tube, one finds analytically an enhancement in the heat transfer across a tube wall due to the alteration of the flow characters caused by the insertion of a twisted structure. Various biochemical activities are influenced by thermal effects, thus resulting in structural changes as can be seen with thermococcuses [
86]. Thermophiles (heat-loving organisms) are known to favor relatively high temperatures around 60 degrees Celsius.
5. Chirality of Omega Particles
Consider a twisted Omega particle (meta-atom) composed of a conducting material, as depicted in
Figure 5a. This twisted Omega particle consists of a single circular loop with a cut at the two ends to which two finite-length cylindrical wires are attached. It is stressed for a twisted Omega particle that two straight-wire portions lie perpendicular to the plane of a circular loop [
35,
47].
Suppose that a plane EM wave is incident onto such a twisted Omega particle, where the time-oscillatory electric field is assumed to be established parallel to the straight-wire portions. In the meantime, induced currents are established along the whole twisted Omega particle from a simple viewpoint. In turn, an effective time-oscillatory magnetic field is induced in the direction parallel to the straight-wire portions [
29,
32]. This loop current is alternatively called a ‘ring current’ [
14] (pp. 91–93), [
87].
The parallel orientation between the electric current and an effective magnetic field is analogous to what prevails with chiral (unidirectional) transport anomaly [
72,
73,
74]. This transport anomaly is called a ‘chiral anomaly’. Consequently, a twisted Omega particle carries a magnetoelectric coupling [
21,
34,
35]. The induced electric currents within a twisted Omega particle can be handled with the simplest single-electron model of Condon, as seen in [
32,
45] and [
59] (p. 273), where the geometric helical paths occupied by helical nanostructures are replaced by chiral confining potentials [
32,
37,
42].
Under mechanical excitations, the two straight-wire portions in
Figure 5a would experience either compression or stretching, as depicted in
Figure 3. In comparison, the looped portion in
Figure 5a may experience a combination of compression and stretching depending on the geometric relationship between the loop plane and mechanical excitation. In other words, there are differential thermal expansions in different members of a twisted Omega particle, thereby leading to broken parallelism.
Figure 5b depicts an exaggerated view of a deformed configuration for a twisted Omega particle shown in
Figure 5a. Consequently, the resultant chirality parameter varies with the Poisson ratio, namely,
and
.
Suppose that a liquid is uniformly dispersed by an ensemble of twisted Omega particles. This homogeneous mixture makes an example of what we have called a ‘chiral medium’. An embedding (surrounding) medium is alternatively called a solvent. In general, a mean-field theory holds true more accurately for sparsely dispersed chiral media than densely dispersed ones [
29,
46]. From the strong dependence on surface states of nanostructures, the stress states of a twisted Omega particle should be more complicated than those of an elliptically spherical particle [
64]. If such a twisted Omega particle is immersed in a liquid, an intricate interplay is at work between radiation-induced viscous flow, anisotropic strain generation, and capillary stresses [
64].
For a twisted Omega particle shown in
Figure 5a, straight-wire portions could be gradually shortened. Instead, the radius of the loop portion could increase under the action of forces produced by the induced electric currents along the whole twisted Omega particle. Shorter straight-wire portions would lead to larger chirality. According to a naïve idea, increased temperature would reduce the geometric helicity of twisted Omega particles, thereby reducing their EM chirality.
Mechanical deformations such as buckling should be taken into consideration during and after fabrications of twisted-Omega-like chiral objects and other helical structures [
14] (pp. 241–263), [
78]. Referring
Figure 5a,b, it will be extremely interesting to examine the EM chirality of a twisted-Omega-like particle composed of auxetic media with negative Poisson ratio, namely,
[
71].
In the higher-order CRs given by Equation (6), the terms
and
represent nonlocal contributions [
41]. It remains to see how the deformation presented in
Figure 5a,b is adequately described by such nonlocal terms.
As compared to plasmonic systems, all-dielectric systems come with lower losses so that dielectric chiral meta-surfaces are actively pursued in recent years. These benefits made possible by all-dielectric systems demand dielectric materials of higher refractive indices, say, niobium pentoxides [
14] (pp. 91–93). In this connection, we need data for not only heat capacity but also enthalpy of formation and Gibbs energy [
88], which are necessary for accounting for conformational changes.
What about twisted Omega particles composed of non-metallic materials? An answer to this self-raised question is obtained by examining optics for all-dielectric systems. An all-dielectric system here refers to, say, a dielectric structure sitting on a dielectric substrate [
47], both being laid down in vacuum. Simply put, even all-dielectric systems could exhibit both electric and magnetic multipoles [
59] (pp. 217–242), if illuminated by non-simple EM fields. This fact was demonstrated by the Mie scattering off a dielectric sphere immersed in an embedding dielectric medium [
26,
89]. Here, the embedding medium is often treated as lossy [
26]. The way this all-dielectric optical system gives rise to a magnetoelectric coupling is by means of the interference between an incident field and a scattered field [
41,
89]. Of course, the Mie scattering off a dielectric sphere immersed in a chiral medium shows a clear magnetoelectric coupling [
55].
Consider a unit cell of a ‘U-shaped loop by two T-shaped strips’ (‘U-shaped loop’ for short) presented in Figures 2 and 3 of [
49]. This U-shaped loop is composed of conducting and non-gyrotropic material. Due to its geometric symmetry, this U-shaped loop is mirror symmetric (thus being achiral). However, an electric transistor is loaded onto one arm of the U-shaped loop portion.
Resultantly, an electric loop current along the U-shaped loop portion is prohibited from flowing in a certain direction, leaving an electric loop current only in one direction along the U-shaped loop portion. The resulting nonreciprocity or unidirectional electric current in [
49] is thereby established. Therefore, a metasurface can be built up by an array consisting of such ‘transistor-loaded’ U-shaped loops. This nonreciprocity effectively gives rise to EM chirality owing to the non-antisymmetric transistor.
Although this idea is worthwhile, it remains to further miniaturize the unit cell such that it works with higher frequencies. The addition of an electric transistor also demands extra fabrication cost as well. Recently, a variety of Omega particles have been proposed thanks to modern nanofabrication techniques. Meta-surfaces consisting of such twisted Omega particles on substrates are examined by [
14] (pp. 241–263) and [
29,
45,
90]. Such WM waves across multiple media involve complicated algebras for both reflections and transmissions [
53,
56,
84]. For instance, the Brewster angle is not clearly defined due to the inherent TE–TM coupling for chiral media [
53,
90].
Figure 5c illustrates an untwisted Omega particle, where both straight-wire portions and a circular-loop portion lie on the same plane [
29]. Hence, an untwisted Omega particle is mirror symmetric. This symmetric structure can be modified by introducing a certain degree of asymmetry. Unlike the 3D twisted Omega particle shown in
Figure 5a, this single untwisted Omega particle shown in
Figure 5c is 2D and is assumed to be very thin.
Figure 5d–f illustrate pairs of two-layer untwisted Omega particles, where the plane of the red untwisted Omega particle lies below the plane of the black untwisted Omega particle. Each pair in
Figure 5d–f is quasi-3D, although the constituent two untwisted Omega particles are assumed to be 2D. Depending on the relative orientation angle of the two overlapping layers, a pair becomes more chiral from
Figure 5d through 5e to 5f [
48]. In the case of thermally induced deformations, the behaviors of the pairs shown in
Figure 5d–f would be rather different.
Likewise, any pair of symmetric 2D meta-atoms can be arranged in a two-layer configuration with a nontrivial relative angle, thus resulting in a chiral meta-atom. For instance, origami systems including shuriken structures [
91], split-ring resonators or simple square-shaped 2D meta-atoms can be overlapped [
50,
87]. A two-layer metamaterial of anisotropic chiral fishnets could be fabricated by allowing for a certain relative angle between the two layers [
21,
40,
41,
47]. Moreover, the periodic arrangement on each layer of the two-layer system could be chosen in different manners [
40].
See Figures 1 and 3 of [
91] for comparison. The purpose of constructing such two-component 2D and/or quasi-3D DNA nanostructures in [
91] is to explore achieving switchable Boolean arithmetic and reaction directionality.
We find in Figure 5 of [
91] that a four-unit tetramer can be arranged in seven alphabet-letter configurations of T, I, O, J, L, S, and Z when they are placed on a 2D plane. In addition to those dimers in [
91], a multitude of multimers can be envisaged for purposes of realizing switches and information manipulators. To this goal, proper linking functionalities among designed multimers should be taken into consideration. Here, temperature control would help establish desired switching and/or manipulations.
Consider molybdenum disulfide
[
92]. Apart from a monolayer configuration of
, its two-layer configuration offer an interesting case of electron–phonon interactions. Those interactions are influenced by the temperature through the Bose factor defined in Equation (1). The resultant photoluminescence absorption is hence dependent on temperature through electron–phonon interactions. Analogously, molybdenum diselenide
as a transition metal dichalcogenide (TMDC) offers functionalities in photochemistry, electrochemistry, and solar cells [
93]. Here, its optical absorbance in the near-infrared (NIR) range is useful for biosensing [
33]. As 2D materials, both molybdenum compounds are susceptible to temperature-mediated deformations although many desired features could be exploited thanks to low dimensions as with graphenes and carbon nanotubes.
It should be stressed that two untwisted Omega particles can sit on the same plane, as illustrated in
Figure 5g. Due to the relative angle between the two untwisted Omega particles, this pair constitutes a chiral structure. Likewise, regularly arrayed achiral atoms could turn into chiral arrayed atoms due to thermal effects, as depicted in Figure 2b of [
66].
Table 3 summarizes various meta-atoms composed of Omega particles. It is helpful to compare
Figure 5 to
Table 3. On the row of ‘fabrication’, it is stressed that a single twisted Omega particle is the most difficult to fabricate. In the last row, the inter-layer distance determines the inter-layer coupling strength in the case of a pair of untwisted Omega particles. Especially when the inter-layer distance is on the order of atomic scales, the temperature-mediated electron–phonon interactions pose a great challenge for theoretical analysis [
92,
93].
6. Chirality of Flat Fishes
Still debatable is the origin of life, which involves, for instance, early selection and early evolution [
44,
94] (pp. 95–129).
A phonon-induced dephasing was supposed to provide a clue as to the extra-terrestrial origin of life [
95]. Quantum models of [
95] were constructed with the help of molecular chiral states and double-well energy potentials (with an energy difference between the two depths of double wells). Consequently, complete racemic states are found to seldom prevail (either left or right chirality survives). In other words, there is always a population inversion; however, it may be small. The ‘cold prehistory of life’ was thus constructed over temperature ranges below the Debye temperature. Moreover, incoherent tunneling between the two wells and losses to surrounding environs are included. Interactions between chiral molecules and underlying phonons will be crucial for more detailed analysis, where temperature comes into play as well.
Consider the placement of a human appendix employed in anatomy. An appendix is placed not on but sidewise from the median plane. In other words, as far as the placement of human internal organs is concerned, humans are chiral, namely, non-mirror symmetric across the median plane. This placement is thought to be determined already in the embryonic stage. This chirality could be partially explained by the formulas presented in Equations (7) and (8) of [
95]. Let us call such an embryonic selection an ‘innate selection’.
In comparison, left- or right-handedness of human arms are thought to be largely decided during the childhood of a human. As far as human arms are concerned, humans are again chiral. Let us call such a selection a ‘postnatal (acquired) selection’. Such postnatal selections reflect more of the interactions between living matters and their environment and society in comparison to the innate selections.
Table 4 compares the innate and postnatal selections.
The chiral pair of snails is familiar to everyone as regards the left- and right-handed helical configurations of snails. The embryonic development entails a selection of one of the two helical shapes, which has been well documented by modern measurement techniques in [
96]. We stress that such an apparently random selection of one of the two helical shapes takes place in the embryonic stage during the lifetime of snails.
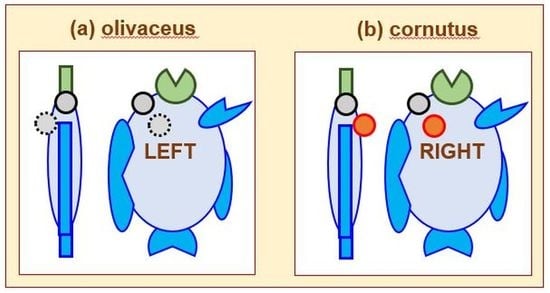
We take below another interesting instance of postnatal selections in flat fishes living in sea water. In this connection, let us quote a famous Korean phrase often cited by Korean fishermen: ‘left-Gwang-right-Do’ [
97]. Here, ‘Gwang’ refers to the fish ‘Gwang-Uh’ in Korean, which refers to ‘Paralichthyidea olivaceus’ in official terms (being called just ‘olivaceus’ here for simplicity). In the meantime, ‘Do’ refers to the fish ‘Do-Da-Rie’ in Korean, which refers to ‘Pleuronichthys cornutus’ in official terms (being called just ‘cornutus’ here for simplicity). Therefore, let us rephrase ‘left-Gwang-right-Do’ into ‘left-eyed-olivaceus-right-eyed-cornutus’ from now on.
These flat fishes are quasi-3D enantiomers in sizes on the order of 15 cm by 25 cm. In comparison, their thickness is about 4 cm. Arrays of those fishes could be dried on flat panels or roofs as with meta-surfaces for later storage. Meanwhile, EM waves of wavelengths on the order of 1 m (radio waves) or longer could recognize 2D arrays of those fishes as chiral meta-surfaces.
With
Figure 6, let us examine the details of either mirror symmetry or mirror asymmetry for these flat fishes.
Figure 6a illustrates a baby fish swimming freely in seawater. As it grows up within a year or so after it was hatched from an egg, its genetic codes advise it to stay on the sandy bottom of a sea, normally located about a couple of 100 m deep. So begins its life near the sea bottom. Sometimes it flips itself or swims. Other times, it tries to catch smaller fishes by maneuvering through seawater.
However, it spends most of its time on the sea bottom. Hence, its body becomes flatter with time, as illustrated in
Figure 6b. It still has a finite thickness, but it becomes almost 2D-like within a year or so. In other words, such flattening deformation is certainly postnatal. Such a flattening compression process due to hydrostatic pressure in the deeper sea might have taken with
, as depicted in
Figure 3c, a growing process superimposed.
Figure 6c schematically shows key portions of a grown-up flat fish, where several representative fins are marked such that ‘af (anal fin)’, ‘df (dorsal fin)’, ‘pf (pectoral fin)’, and ‘tf (tail fin)’. Notice here that the abdominal portion carries the ‘af (anal fin)’, while the back portion carries the ‘df (dorsal fin)’.
Figure 6c is intentionally drawn to carry only a single eye.
While being laid down near sea bottom, a flat fish would feel that one of its two eyes receives almost no light since that bottom-facing eye almost touches the bottom. The flat fish thus adjusts the placement of the two eyes toward the sunlight. It is because turning itself upside down at regular time intervals is probably more energy consuming than altering the placement of eyes permanently. Such a rearrangement of eyes might have taken place in the early portion of its lifetime (being only a few years). This fact corroborates the postnatal selection of eye placement. Receiving more sunlight is interpreted as an adjustment to environmental effects.
Notice in the preceding paragraph that the amount of light shed on a flat fish over a long time alters the achiral shape of a flat fish. This difference indicates a long-term thermal effect due to the thermal energy added to a flat fish of chiral shape.
Figure 6d,e present two ways of rearranging its eyes.
Figure 6(d1,e1) show the top views as seen from the ‘df (dorsal fin)’ on the backside of a flat fish. From these top views, the eyes of an ‘olivaceus’ are shifted to the left, as depicted in
Figure 3(d2), whereas the eyes of a ‘cornutus’ are shifted to the right, as depicted in
Figure 3(e2).
Two different kinds of flat fishes illustrated in
Figure 6(d1,e1) are mirror symmetric with each other across a certain mirror plane that is parallel to the median planes that pierce the respective fishes along the ‘df-af’. Notwithstanding, a mirror symmetry of a certain flat fish should be determined by examining a mirror symmetry about a mirror plane that pierces through only a certain single fish. There is hence no mirror symmetry for a certain lone flat fish with one-sidedly displaced eyes.
Consequently, both kinds of flat fishes illustrated in
Figure 6d,e are, respectively, mirror asymmetric or chiral, thereby forming an enantiomeric pair. This postnatal chirality is established over a period of a year or so for a flat fish is analogous to the fabrication process of various nano-scale chiral objects [
6]. In addition, it remains to identify other characteristics such as chiral centers, enantiomers, diastereomers, and higher-order enantiomers by working out more details of the above schematic
Figure 6, as has been performed in [
5].
Are there additional features that come with left- and right-handed eye pairs of flat fishes? Yes, there are. A left-handed olivaceus, shown in
Figure 6d, is known to possess a larger mouth than a right-handed cornutus, illustrated in
Figure 6e. Likewise, the former possesses stronger teeth than the latter. The ratio of the total numbers in olivaceus and cornutus may indicate which kind of flat fishes are endowed with better survivability and adaptability to nature. In general, it is known that olivaceus is more available in nature than cornutus.
Such differences in stability and adaptability are also found in many pairs of chiral biopolymers in the sense of enantiomeric excesses [
94,
98]. The inter-helix interactions play a great role in determining such a stability [
98]. Models of [
95] can also be expanded and modified for this purpose.
We emphasize that the chiral features of flat fishes are acquired mostly postnatal. In this respect, the optical properties of chiral media may undergo temperature-mediated variations in terms of both configurational and material properties. Such property changes are considered as ‘post-fabrication’, which leads to alterations in the corresponding constitutive relations employed in the Maxwell equations.
7. Other Examples in Elastic Deformations and Electron Dynamics
Consider a helix shown in
Figure 1d, where pitch
, wire radius
(in
Figure 1a), and helix radius
are indicated [
15,
37,
42,
45,
99]. Under some external excitations, a helix could be gradually shortened into a helix with shorter straight-wire portions. Instead, the helix radius gets increased with a resultant shorter pitch. This decreased pitch may be achieved under the action of forces produced by the induced electric currents along the helix. These forces is supposed to be caused by Coulomb repulsion, although Coulomb force may be incompatible with material chirality [
59] (p. 208). Roughly speaking, the helix under induced currents gets less chiral from the viewpoint of EM waves.
Figure 1d depicts approximately a single-stranded DNA as another example of chirality. As biological materials, double-helix (double-strand) DNAs (deoxyribonucleic acids) are the most notable twisted structure [
91]. A twisted Omega particle, as depicted in
Figure 5a, is receiving renewed attention, partly due to its resemblance to DNAs [
45].
Consider the chirality-induced spin selection (CISS) [
10,
37,
42,
43,
99,
100,
101,
102]. The CISS refers to the electron transport of a particular spin direction, namely, spin polarization. DNA-like helices of finite length are described by a Hamiltonian composed of several constituents: (i) a molecular portion (a potential and a kinetic portions), (ii) a spin-orbit coupling portion, (iii) an electrode portion, and (iv) a dephasing portion due to electron–phonon and electron–electron interactions [
99].
Input–output formulations are examined in [
101,
102]. Couplings between a straight waveguide and a helix-shaped waveguide are examined from the viewpoint of CISS [
101]. Here in [
101], an important role is played by the finite-sized (or spatially extended) overlap implying the inter-waveguide or interfacial coupling. In addition, the magnitude of the bi-characteristics, as provided by Equation (4), turns out to be distinct, thereby providing unidirectional propagations. This phenomenon with a two-waveguide coupling is akin either to the CHISPR in [
22,
23] or to the resonance between a chiral medium and a dielectric medium [
21,
55]. Hence, either electron-spin chirality or photon chirality residing in a chiral medium could be transferred to an achiral medium. Especially, two helices are examined for CISSs with the two helix axes intersecting each other by an oblique angle [
101], whence SOCs are more clearly investigated.
See Figure 1 of [
102] for the distinction between the radial breathing mode (helix radius) and the axial longitudinal mode (helix pitch) for phonon resonances. It is seen in [
102] that the radially polarized electric field is linked to the radial breathing phonon mode. It remains to further assess the relative importance between the direct electron–environ interaction and the indirect phonon-mediated electron–environ interaction [
102].
The reason why CISSs are intensively investigated is that the constitutive relations, as given by Equation (3), might arise from microscopic electron dynamics. This CISS is found to strongly depend on temperature in both biological systems [
43] and magnetic systems. DNAs as deformable polymer chains are analyzed under the influence of thermal fluctuations [
9].
A single-strand DNA can be modeled by the crudest flexible rod. As more realistic features of a DNA are taken into consideration, the resulting temperature-mediated electron–phonon interactions become unwieldy as well [
9]. Consequently, the electric conductivity is found to decrease largely with temperature due to the thermal agitation of phonons [
2] and polarons. However, opposite temperature dependency is also observed under other experimental conditions, including the substrates and electric contacts. In this respect, toehold-free strands of DNA-like structures will make a suitable comparison [
91].
These experimental and modeling results show the importance of incorporating the electron–phonon coupling in the right manner in handling chiral transports through both chiral objects as individuals and chiral media as a composite whole. Such electron–phonon interactions should be of the appropriate form for the nonzero chirality parameter to be established [
32]. To this end, we can consult various results obtained from molecular-dynamics simulations [
7,
65,
71,
103].
Furthermore, the force between two colloidal particles, each of them carrying one single-strand DNA, is theoretically predicted in [
104]. Here, the simplest 1D discrete-node model for phonons is adopted with the coupling force between two strands of a double-helix DNA. Temperature dependence can be incorporated into the model of [
104] by instituting the temperature dependence of both self-spring and coupling springs. In this regard, see [
9] for treating flexible rods and [
65] for shape memory alloys.
Afterward, there appeared numerous investigations into alpha helices. In the case of alpha-helical peptides [
99], the directional electron transport is called ‘spin filtering’. Protein unfolding was examined for helix-bundle proteins dispersed in water [
103]. Upon stretching along the main helical axis of an alpha-helix, an unfolding of a helix takes place to become a beta-strand (or beta-helix), thereby reducing the geometrical chirality [
103]. Heat-induced unfolding is quite understandable from the viewpoint of an entropy increase with higher temperatures.
In other words, the pitch becomes smaller while the helix radius is enlarged because the effective Poisson ratio is positive. See
Figure 5a,b for comparison. Such stretching accompanying unfolding could be heat induced. The stability of an alpha-helix depends on the interactions with an embedding (surrounding) fluid, namely, in the sense of hydrophilicity versus hydrophobicity. See [
44,
65,
103] and [
94] (pp. 95–129). The foldability considered in protein folding stands for the relative importance among various interactions and geometric conformations for protein constituents [
44,
103].
In addition, the magnetoresistance ratio exhibits strong temperature dependence in not only double-stranded DNAs but also alpha-helix oligopeptides [
43]. In a similar line of reasoning, a chirality-controlled (selective) synthesis (CCS) offers us a challenge in fabricating carbon nanotubes of a certain desired handedness [
7].
Table 5 summarizes various examples handled in this section. Most biological matters are soft matters (e.g., in a variety of polymers) [
58], thus undergoing conformational changes depending on several factors: the environmental temperature, strains caused by nearby biological matters, embedding fluids, etc.
As a kind of typical soft matter, chiral lyotropic chromonic liquid crystals exhibit their helical pitches increasing with temperature [
105] when placed within amino acid solutions. Helical pitches increasing with temperature refer to a decreased geometric chirality. However, an opposite temperature dependence is observed for other kinds of liquid crystals. Such mixed temperature–pitch relations render our expectations on
extremely confusing for helical structures. When a droplet of chiral liquid crystal (LC) is immersed in an achiral isotropic liquid, rotational and helical motions due to local deformations can be identified within a finite-sized chiral LC droplet [
5,
16].
Notice in this aspect that shear stresses normally lead to either rotational motions or crystal reorientations [
65,
66,
68,
106]. In the area of atomic bonding within a molecule, the rotary motion around a double-bond axis (between a rotor and a stator) characterizes the first-generation molecular motor, as illustrated in Figure 2 of [
100].
Meanwhile, molecular motors shed light on the relationship between deformation dynamics and energetics. See [
44,
106,
107] and [
59] (pp. 17–21). For instance, we find light- and heat-induced consecutive isomerization [
100]. Molecular motors operate by being stepped through a repeating cycle of chemical reactions while undergoing shape changes and executing their own movements.
Molecular motors are driven either by light or by chemical reactions [
100,
108,
109,
110,
111,
112,
113], thus being sensitive to temperature changes. Mechanical effects are sometimes accompanied by energetic effects and chemical reactivity [
8]. Generically speaking, spontaneous chemical reactions are unidirectional (chiral) [
109]. For instance, a paper is burned to ashes, but the reverse hardly takes place. In other words, there is a kinetic asymmetry, and reactions proceed out of detailed balance. In this respect, an enantioselective catalyst helps such a unidirectional process to proceed faster [
109]. The collection of reactants signifies a certain extreme chiral state, while the collection of reaction products signifies the other extreme chiral state. A net directional motion is hence desired for molecular motors.
Chemically driven molecular machines are governed possibly by the kinetic asymmetry as a kind of Brownian ratchet. Thermally driven ratchet motions are also reported for magnetic materials [
17]. Moreover, ratchet functionality is allowed mostly in out-of-equilibrium conditions [
109,
111,
112]. In this connection, one exemplary motion is either a rotation around a bond (one of the internal axes) or a motion along a track [
108,
109,
113]. Notice that unidirectional motions are more useful than uselessly twitching back-and-forth two-way motions [
107].
Mechanically interlocked molecules (MIMs), such as catenanes or rotaxanes, offer chances of directed motions by way of dissipating supplied energy in a proper fashion [
111]. A directed motion on a linear track translates into either clockwise or counterclockwise rotation on a circular track [
17]. Here, chirality refers to dynamical properties.
In terms of light polarization, a linear, directed motion corresponds to a linear EM polarization, whereas a circular, directed motion corresponds to a circular EM polarization (either clockwise or counterclockwise) [
28]. It should be kept in mind that such ratchet (unidirectional, chiral) rotational motions could be sustained only in thermal out-of-equilibrium conditions rather than in thermal equilibrium [
17]. By the way, spatial thermal gradients are associated with thermal out-of-equilibrium conditions. Reaction-kinetic asymmetry is key to understanding the directionality of kinetic cycles. Likewise, geometric chirality is a key to causing asymmetry in light-driven processes.
In the case of photo-responsive processes, power strokes are involved in driving light-driven molecular machines through the absorption of external photon energy [
106]. Light excites a molecular machine into a high-energy state, while its relaxation causes mechanical deformations. The employed photochemical principles in light-driven motions invariably involve temperature dependence and losses in device performance.
In terms of sub-molecular structures, there is enough conformational flexibility in the stator of a molecular motor to prevent excessive distortion of the central bond, which could lead to rapid racemization (becoming achiral) [
113]. In the case of overcrowded alkene-based molecular motors [
106], there are two aspects with respect to chirality: (i) photochemical E-Z (PEZ) isomerization and (ii) thermal helix inversion (THI) steps [
15,
100,
108,
113]. Resultantly, conformational chirality is likely to lead to unidirectional rotations [
113].
Consider silicon-based optical materials employed for chemical and biological sensing in the mid-infrared wavelength range [
114]. Here, the fundamental vibrational modes of most chemical bonds are of prime interest. Both molecular motors and molecular switches require largely transient dynamics rather than time-harmonic periodicity for motion analysis. We find many revenues in controlling the rotation speeds of molecular motors.
The allosteric regulation is based on proper selections of binding sites, where symmetry and chirality of participating geometric shapes play crucial roles [
113]. Such allosteric bindings are sensitive to local strain fields around the binding sites. In brief, the ideas underlying molecular motors could be adopted for implementing tunable and controllable optically chiral nanostructures.
We find an electron-spin chirality in conducting polymers. Such dimers are adequately described by the famous Su–Schrieffer–Heeger (SSH) model [
1,
115,
116,
117,
118,
119]. To the first approximation, an SSH model accounts for the interaction between electrons and phonons, while the inter-electron Coulomb interactions are considered higher-order corrections. The environmental temperature affects the vibrational modes of phonons.
Figure 7 illustrates a 1D SSH model [
1,
115,
116]. Moreover, there are 2D SSH models, for instance, those of [
117,
118]. Hidden behind a 1D SSH model are, however, 2D features [
116] that account for dimer configurations. Under additional constraints, a simple analysis shows us that an energy band gap opens only for
, namely, intercell coupling being greater than intracell coupling. Accordingly, only the case with
leads to nontrivial unidirectional (viz., chiral) propagations of electron waves [
1,
118].
Moreover, a ground state for phonons is described by a staggered set of elastic displacements along an SSH chain [
115]. The associated sound speed of phonon vibrations can also be analytically found, especially while accounting for intercell bond stretching.
An original SSH model has been established for an infinitely long SSH chain. However, advanced models account for finite-length SSH chains. The end conditions necessary for describing such finite-length SSH chains reflect the environmental effect. Such end conditions for finite-size effects are in some sense analogous to contact potentials employed in handling finite-sized DNA-like helical structures [
10,
37,
42,
101].
All the preceding discussion on the SSH models is intended to show that temperature variations might affect in different manner so that the nontrivial case with at a certain temperature might turn into a trivial case . It is because intracell coupling and intercell coupling could variously respond to temperature variations.
A 1D photonic SSH model has been realized by arranging micropillars of finite length in two rows and on a substrate [
119]. In this aspect, compare
Figure 5c to
Figure 5d–f. In practice, this special photonic SSH model of [
119] occupies a 3D space.
The initial introduction of alpha helices came with the notion of a rotation around a helical axis and a translation along a helical axis [
98]. It is noticed in this regard that a homogeneous wire-like thread admits no residue (or residue being zero) when it is deformed into a helix. In addition to the pitch and helix radius for defining a single homogeneous helix, there are more geometric parameters for defining relationships among constituent (or contributing) helices if sub-helix constituents are looked upon.
For such spatially inhomogeneous helices, residues per helical turn are found to be non-integers in general. For instance, each amino acid corresponds to a helical turn over the angle of
in the helix. Therefore, its helix has
residues per turn [
94] (pp. 95–129).
Coiled coils are a set of helices put together in diverse configurations, where the helical axes are aligned in pseudo-parallel fashions. Coiled coils are alternatively called ‘compound helices’ or ‘superhelices’ [
94] (pp. 95–129). For instance, double-strand DNAs can be considered the simplest form of coiled-coil bundles. The larger the number of coiled coils, the larger becomes the number of geometric parameters defining the whole coiled-coil bundle.
With increasing number of elemental coils, there could appear a numerous variety of coiled-coil bundles depending on how elemental coils are joined together. Such combinatorial complexity is common to the formations of oligomers. Even braids and sheets are available for the net shape of a coiled-coil bundle. Hence, the net chirality exhibited by a single coiled coil poses a challenge of evaluating the attendant EM chirality from light–matter viewpoints.
With an increasing number of coiled coils, the temperature effects are likely to be worsened in predicting the net chirality of a superhelix. A desirable side effect of a coiled coil is increased mechanical rigidity in comparison to its individual constituent helices. As a macromolecule, a coiled coil admits a variety of conformational deformations, thus altering the apparent mechanical strengths. For instance, we find packing-induced super-helical distortions [
94] (pp. 95–129). Furthermore, alpha helices are found to be predominantly single-handed between left- and right-handed choices. Coiled coils could be employed to realize molecular motors, for which supramolecular polymers can be implemented as well [
109].
Optical activity is also exhibited by natural materials. Quartz is a naturally available chiral crystal, for which the temperature dependence of optical chirality is well documented [
30]. Roughly over the temperature range of
, the angle
for optical rotatory dispersion (ORD) in Equation (5) is known to monotonically increase with temperature. So increases the degree of chirality of the constituent helical fragments with temperature [
30]. There is also a phase transition across a certain temperature range owing to the temperature-modulated phonons [
66,
70]. In brief, the geometric helical property is conducive to the optical chirality for many kinds of crystals.
Vibrational motions of atom-bonding chains can be categorized into rotational and longitudinal ones along the axis of a bridging bond as viewed from stereochemistry. Retrievals of such different vibrational modes are then required in properly interpreting the Raman scattering data obtained on the frequency spectral domain, as seen from [
14] (pp. 53–74) and [
84,
93,
120]. Recall that Raman spectroscopy involves interactions among electrons, phonons, and photons. Likewise, we find phonon–photon interactions with pinenes [
59] (pp. 17–21).
Recall that
exhibits different frequency-dispersive absorptions [
82] in connection with light–matter interactions. For semiconducting states of
compounds, the light absorption into solids depends on the types of electronic interband transitions: forbidden versus allowed [
82,
84]. In this connection, we learn in the case with
[
84] that the effective refractive index depends strongly on the wavelengths of EM waves since the interband transition depends on the photon energy. The involved bandgap energy depends, in turn, on temperature [
84]. See [
120] for other electro-optic materials.
Consider then electromagnetically induced transparency (EIT) as another example of light–matter (or atom–field) interactions [
121] (pp. 220–247). The EIT is traditionally examined in the context of three-level systems and electric-dipole approximation for the atomic transitions. Only allowed atomic transitions are taken into consideration, while forbidden atomic transitions are not considered due to the quantumness of atomic transitions. This dichotomy into allowed and forbidden transitions is essential to chiral quantum electrodynamics (CQE), as previously considered in [
10,
11]. Moreover, the usual technique of rotating wave approximation (RWA), as employed during the solution for EIT is also incorporating an aspect of such CQE.
Under the category of atom–laser–field interactions, Raman transitions through an ensemble of atomic vapors were investigated by [
36] to assess optical chirality. To this goal, a five-level system or an effectively four-level system was devised to improve upon the idea of EIT. In this way, a nonzero absorption
of the chirality parameter in Equation (3) was theoretically estimated in terms of the atomic density and other parameters. Resultantly, conditions were identified in [
36] for negative refractive indices to be established such that
according to Equation (4).
As seen from the Bose factor introduced by Equation (1), the Raman spectra are indicative of the temperature dependence of various vibrational modes of phonons [
92,
102,
120]. For helix-shaped structures, it is necessary in general to infer from the Raman signals the desired structural information, such as pitches and radiuses [
2,
3,
4,
5,
6]. Such data extraction constitutes inverse problems from a mathematical point of view.
Recall the transverse mode instability [
77] that was previously discussed in connection with ovalization and the Poisson ratio. The heat-transfer enhancement due to a thin twisted tape, as considered in [
85], is linked to the transverse flow-speed component. In this respect, a helical lining was introduced inside a gun barrel, thus leading to a bullet endowed with both linear projectile speed and rotational speed. The resulting helical trajectory of a bullet is dynamically more stable than a straight trajectory for a bullet being ejected from a smooth inner barrel. The chemical energy of a gun powder is hence divided into linear kinetic energy and rotational energy for a helically traveling bullet, whereas it is mostly of linear kinetic character for a linearly traveling bullet. See the energy partition discussed in [
23].
A frisbee makes largely a curved flight path due to its chiral shape. The cross-section of a typical wing of an airplane is certainly chiral, thus converting a portion of the thrust in the main flight direction into a lift in the transverse direction. This Magnus effect is a fluid-mechanical version of both the electronic Hall effect, magnon Hall effect [
17], and optical Hall effect [
90]. The key idea behind such flying objects is a longitudinal-to-transverse conversion. Screws beneath a boat work according to a similar principle.
8. Discussion
Having considered thermal effects on various chiral objects, let us turn once again to a chiral medium, namely, an ensemble of chiral objects dispersed into an embedding fluid (either liquid or gas). Suppose this time that an ensemble of chiral objects may consist of several kinds of enantiomers.
For the sake of simplicity in the discussion,
Figure 8 shows two comparative situations, where blue lightning-rod-like objects and red crescent-like objects stand, respectively, for left-handed enantiomers (denoted by ‘−’) and right-handed enantiomers (denoted by ‘+’). Both ensembles here consist of blue and red objects but in different proportions.
For further simplicity, suppose that blue and red objects are more stable, respectively, at lower and higher temperatures. Therefore, the blue objects undergo thermal helix inversion (THI) with increasing temperature, thereby becoming red objects. Such THIs between blue and red objects arise from several factors: conformations, thermoelastic properties, electron dynamics, energy contents, etc. In general, both blue and red objects are not necessarily enantiomeric counterparts of each other, for instance, being composed of varying sizes. In addition, solute–solvent (i.e., system–environ) interactions may not be negligible [
108].
In the case of supramolecular polymers based on N-triphenylamines (TPAs) [
122], the interconversion among their variants TPA-1, TPA-2, and TPA-3 determines the net chirality. Those composite chiral media yield distinct characteristics of optical activity, such as ORD, in terms of temperature, as seen in Figure 3 of [
15]. Here, a comparison is made between toluene and chloroform. The enantiomer concentration alluded to by [
123] refers to the concentration of, say, a left-handed enantiomer among a mixture of left- and right-handed enantiomers. Therefore, the concentration of the total enantiomers with respect to the embedding medium, not treated by [
123], should be taken as an additional factor determining the net chirality.
According to the above simple picture in
Figure 8 and the constitutive relations in Equation (3), a helical inversion temperature of
as a transition temperature is defined below.
The converse can be envisaged such that red objects turn into blue objects with increasing temperature. In this converse case, the inequality signs in Equation (8) are reversed, of course. In general,
depending on a particular combination of an embedding medium and dispersed chiral objects. There exists an enantiomeric excess if either
or
[
8,
32]. The condition either of
or of
is called the ‘equal-population condition’ between left- and right-handed enantiomers.
An example of such transition is discussed in detail for a solution with a variety of polymers as solutes dispersed in various solvents [
15]. They considered a polymer consisting of enantiomers of opposite chirality in unequal amounts. Such a (nonracemic) chiral polymer could undergo a temperature-dependent transition toward a net achiral (racemic) polymer. That transition temperature is called a compensation (switch) temperature, namely, either of
, thus delineating a temperature-dependent helical sense inversion or thermally activated helical reversal [
15]. In this respect, the solute–solvent interactions should be carefully examined, as in the case of capillary flows.
Helical polymers can be appended with paired structurally different enantiomers. A group of monomers of different species is called a copolymer (for example, terpolymers and quaterpolymers) [
15]. Such conformationally flexible structures could have opposing helical sense preferences. As illustrated in
Figure 8, consider a solvent dispersed with two groups of constituent chiral objects [
15]. Such a chiral solution exhibits varied helical sense excesses (HSEs) depending on the two constituent solutes: (i) relative molar compositions and (ii) relative chemical energies.
A mixture of spin-up electrons and spin-down electrons can also be described in
Figure 8, whence a one-way spin-dependent channel could be opened for spintronics applications. See [
11] and [
14] (pp. 53–74). Recall additionally that there could exist a transition with
for the Poisson ratio as stated in Equation (8). Notwithstanding,
and
in general.
Our interest in the interaction between EM waves and chiral media lies in how to make a certain chiral medium straddling a racemic mixture, namely, switching between a chiral medium in one direction and another chiral medium in the opposite direction. By a slight modification of dispersed chiral objects, the chiral medium undergoes a switching between two opposite chiral states. From the viewpoint of optical sensing of chiral media, either
or
is termed an ‘optical switch temperature’ [
15]. The majority rule (referring to a higher concentration between left- and right-handed enantiomers) is hence applied to determine optical activity from a mixture of left- and right-handed enantiomers [
15,
32].
Helix reversals in polymers are investigated through a random-field Ising model so that the Ising order turns out to correspond to optical activity [
15,
123]. In this way, the optical activity of a helical polymer is evaluated in terms of the magnetization of a random copolymer. Optical activity can thus be evaluated in terms of enantiomer concentration [
123]. We notice particularly that a finite domain size comes into play, and hence, boundary effects should be taken into consideration [
123]. This boundary effect is akin to solvent–solute interactions.
There is a possibility of interconversion from a left-handed enantiomer to a right-handed enantiomer or vice versa. Such a thermal (heat-induced) helix inversion (THI) is found in helical diastereoisomers, where chirality undergoes cyclic sign changes according to the pattern
. This inversion is associated with the variation in the dihedral angle around a certain bond between two atoms so that it affects the rotational speed of a molecular motor [
108,
113]. From an energy viewpoint, a helix inversion barrier should be overcome. Such alternating chirality variations can be exploited for realizing the aforementioned molecular motors and switchable spin filters [
28,
91,
100,
106,
108]. Magnetic contents of helical structures also affect the helix inversion [
10].
As regards effective-medium theories (EMTs), we learn that there are no systematic endeavors for an EMT for chiral media. Derivation of such EMTs will be more challenging if there are more than two kinds of constituent chiral objects dispersed in an embedding medium [
4]. An extra complication arises from the interactions among the embedding medium and embedded objects if the volume density of embedded objects gets larger [
32,
47,
48].
In the case of vortex chaoticons established in thermal nonlocal nonlinear media [
124], thermal effects are accounted for by a diffusion term within a nonlinear Schrödinger equation.
Our discussion on flat fishes shown in
Figure 3 gives us some clues as to how to construct chiral metamaterials and chiral meta-surfaces in bio-inspired fashions. There could exist 2D meta-surfaces, where the meta-atoms (building blocks or unit cells) are also 2D. When meta-atoms are composed of a single homogeneous medium, the chiral meta-atoms are normally 3D, namely, non-planar [
5]. Notice however that planar chiral materials are allowed in stereochemistry where a variety of atoms participate in forming varied materials such as in heterostructures and superlattices [
5,
71]. Only through effective-medium theory [
84], a metasurface consisting of 3D meta-atoms appears to be 2D for sufficiently long-wavelength EM fields [
90].
An exact balance as found in racemic mixtures between two kinds of enantiomers is thought to be an exception rather than a rule in nature [
8], where one kind of enantiomers is often favored over the other kind of enantiomers. It is said in [
5] that an exact symmetry (achirality) is close to death. In this regard, we raise a self-question as to whether the vacuum fluctuations, as seen in quantum mechanics, have something to do with the nonzero enantiomeric excesses [
59] (p. 208). A possible answer to this self-question transpires to the unachievable state of absolute zero temperature, which in turn corroborates the importance of phonon dynamics and statistical features. See [
14] (pp. 8–20) and [
17]. Indeed, an achiral mirror-symmetric state is the rarest situation as exemplified by our study on two obliquely colliding EM waves [
51].
Mesogenic matters have also been investigated for their diverse roles in both geometric helicity and EM chirality. Whether a chiral object retains its given optical chirality at low temperature remains still tricky because of the quantum weak interactions [
59] (pp. 207–203), [
95].
We have previously mentioned that liquid crystals (LCs) of geometrically helical structures [
5,
15,
16,
105] are susceptible to temperature variations. In this regard, thermal stability denotes an ability of a chiral structure staying relatively immune to changing thermal environment [
125]. Suppose that chiral dopants are added to a nematic LC host [
125], thus forming a cholesteric LC. In the field of LCs, chiral molecular switches are often used to adjust the pitch and chirality of cholesteric LCs. However, thermal effects can lead to the spontaneous cis–trans isomerization of molecular switches, which restricts the thermal stability and further optical applications of cholesteric LC superstructures.
A cholesteric LC could undergo chiral inversion depending on the spectral nature of illuminating light. For instance, geometric chirality inversion could take place when illuminated by either green or violet lights [
125]. We find an associated light-switchable conversion between the spin angular momentum (AM) and the orbital AM of EM waves. Hence, a Pancharatnam–Berry geometric phase is obtainable instead of a conventional dynamic phase. By dynamically adjusting the circular-polarization direction (namely, left- or right-handed) of impinging EM waves, a tunable geometric phase is hence realizable. The thermal effects and attendant variations of optical properties of helical nanostructures could be minimized by judicious designs of helical shapes, which is still left as a topic of further study. One way of enhancing thermal stability is to increase the thermal conductivity of helical nanostructures, by which both residual thermal stresses and thermal non-uniformity could be minimized during thermal transients.