1. Introduction
[1.1.1]Propellane,
1 (
Figure 1), a compound whose structure includes two saturated carbons in which all four bonds are directed into a single hemisphere, was first synthesized in 1982 by Wiberg [
1]. While
1 remains a target of fascination for theoretical chemists because of the unusual bonding arrangement between the two inverted bridgehead carbons [
2,
3,
4,
5], it has also seen recent practical applications for a variety of synthetic purposes [
6,
7]. There has been ongoing interest in the possibility of synthesizing mono-, di-, and trisubstituted [1.1.1]propellanes by replacing one or more of the CH
2 groups of
1 (see compounds
2–4,
Figure 1) [
8,
9,
10,
11,
12,
13,
14,
15,
16]. Although these substituted compounds remain synthetically elusive, several computational studies have suggested the possibility that they could exist as stable entities [
8,
10,
12,
13]. A computational study on a series of trisubstituted propellanes,
4, was carried out by Pittman using a coupled-cluster approach (CCSD/aug-cc-pVDZ) [
8]. That study identified a number of trisubstituted [1.1.1]propellanes that appeared to be sufficiently stable so as to recommend them as synthetic targets.
Wiberg’s synthesis of [1.1.1]propellane is outlined in
Scheme 1 [
1]. Thus, upon treating 1,3-dibromobicyclopentane,
5, with nBuLi, a metal/halogen exchange process occurs that leads to the formation of the anionic bridgehead bromide intermediate
6. The intramolecular displacement of the second bromine atom forms the strained bridgehead-bridgehead bond. A number of other propellanes have been synthesized in a similar manner [
17,
18], which provides a straightforward and perhaps general means by which to synthesize propellanes, including (potentially) those substituted as discussed above.
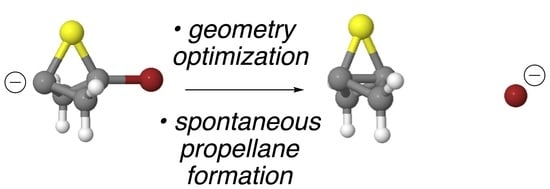
In an earlier computational study, we found that, upon an attempted computational optimization of the geometry of the unsubstituted anionic bridgehead bromide compound
6 at the B3LYP/6-31G* level of theory, it spontaneously formed
1 via an ejection of the bridgehead bromine as a bromide ion during the optimization process [
19]. Thus, compound
6 itself was not a stationary point on the potential energy surface (PES) but led seamlessly to the propellane structure, thereby mimicking the experimental behavior observed by Wiberg. Furthermore, we were able to successfully model a number of other spontaneous formations of propellanes from anionic bridgehead bromide compounds that varied by the number of carbon atoms in the bridges [
19]. Interestingly, however, attempts at forming the [2.2.2]propellane
8 (see
Scheme 2) via an optimization of anionic bridgehead bromide
7 was unsuccessful, with the central bridgehead-bridgehead bond resisting formation [
19]. This computational behavior appeared to portend the experimental finding that [2.2.2]propellane, formed in a manner similar to that outlined in
Scheme 1, is highly unstable, and unable to be isolated. Additionally, optimizing the geometry of the [3.2.2] anionic bridgehead bromide
9 resulted in the loss of the bromine atom as a bromide ion, but with bond scission (i.e., a Grob fragmentation) to form the bis-methylene compound
10 rather than the formation of the propellane [
19]. Interestingly, a similar Grob fragmentation process had been observed as the means of decomposition of
8 as well as several other propellanes [
17,
20]. While [3.2.2]propellane has been synthesized and characterized [
21], it was not synthesized via an anionic bridgehead precursor, so it is not known whether it would undergo a Grob fragmentation under those reaction conditions. Overall, then, it appeared that computational modeling did a remarkable job of predicting known experimental results.
In Pittman’s study, the feasibility of formation of the substituted propellanes
4 was based solely on the anticipated strain energies of the final propellane structures [
8]. Modeling the final propellane product may indicate whether the propellane has any chance of existing or not, but it provides no indication as to whether there is an energetic driving force for the formation of the central bond. The computational optimizations discussed above provide this information, as either the central bond will be formed, or not, depending on whether the propellane is at lower energy relative to the anionic bridgehead bromide, and as long as there is a viable energetic pathway that allows for its formation. If such a viable energetic path exists, we would expect spontaneous ejection of the bromine as a leaving group and the formation of the substituted propellane upon geometry optimization. The synthetic pursuit of these substituted [1.1.1]propellanes would, therefore, be most promising. If a viable energetic path does not exist, we would expect that either the anionic bridgehead bromide would optimize as a stationary point of its own (i.e., it does not lead to propellane formation), or another pathway may be followed other than that of the propellane formation (e.g., such as Grob fragmentation). These substituted propellanes would either not be attractive to pursue synthetically (especially if the strain energies of the propellane structures themselves are particularly high), or they should be pursued using a synthetic method other than via anionic bridgehead bromide precursors.
In the current study, we have modeled a series of anionic bridgehead bromides substituted at one, two, and all three of the bridging CH
2 groups of
6 to observe whether they would spontaneously form the corresponding propellanes upon optimization. We chose many of the same groups as earlier investigated by Pittman to allow for direct comparison with those findings. In addition, we have analyzed the strain energies inherent in all of the proposed propellanes and have attempted to correlate the strain energies with the propensity to form propellanes upon geometry optimization of the precursor anions. Based upon this work, we are able to recommend pursuing the synthesis of those propellanes most likely to be successfully formed via the synthetic method outlined in
Scheme 1.
3. Results and Discussion
Pittman selected the CCSD computational level of theory for modeling a series of substituted [1.1.1]propellanes
4 [
8]. Unfortunately, however, this level of theory is exceedingly time and resource expensive, especially when using it to model the (often) many iterative steps required to eject the bromide ion from the anionic bridgehead bromides to form the resulting substituted [1.1.1]propellanes. We had used density functional theory (DFT) successfully in our earlier work [
19], and we decided to continue using DFT. However, we opted to switch from the B3LYP functional we had used earlier to the more robust ωB97X-D functional, which provides the benefit of including dispersion effects that are absent in B3LYP but could be of importance during the geometry optimizations [
25]. Additionally, the ωB97X-D functional has been used in a number of recent studies by others to successfully describe the reactivity of propellanes and related structures [
26,
27,
28]. We used the same basis set (aug-cc-pVDZ) as employed by Pittman as it includes diffuse functions that are important for the accurate modeling of anions. Furthermore, this basis set is of a size sufficient to model these compounds (as reflected by Pittman’s work), but it is not so large as to make the calculations unwieldly. Finally, we included solvent effects using the polarizable continuum model (PCM) to better reflect the behavior of the ions in solution. Tetrahydrofuran (THF) was selected as a solvent since it is a solvent often chosen for synthetic work with carbanions. All stationary points were tested by calculating the IR frequencies to confirm the absence of any imaginary frequencies.
While Pittman and others have focused on [1.1.1]propellanes substituted at all three of the bridging CH2 groups, we have expanded these studies to investigate the effect of mono- (2), di- (3), and trisubstitution (4) of the CH2 bridges of 1. This allows for understanding the cumulative effect of successive substitution and may indicate whether lesser-substituted propellanes (i.e., 2 and 3) might be more viable synthetic targets than the fully substituted counterparts (i.e., 4).
3.1. Comparison of Computational Methods for Modeling Propellanes 1–4
We began by optimizing the geometries of the neutral substituted propellanes in comparison with previous results by Pittman, where available. In general, the bridgehead-bridgehead bond distances are calculated to be slightly shorter than those calculated using the CCSD method, with the mean absolute difference being 0.037 Å (see column 2,
Table 1). The CCSD method predicted an order of
4O <
4NH <
4S <
4CH
2 <
4CF
2 <
4SO <
4SO
2 for the propellane bond lengths [
8]. The results of the ωB97X-D method are in good agreement with the CCSD results, with the exception of a swap between
4CF
2 and
4SO. However, these two bond lengths are predicted to be close to one another according to both of the computational methods (1.721 and 1.733 for CCSD, respectively, and 1.698 and 1.697 for ωB97X-D). Additionally, the bond length values calculated in this work were nearly identical to several of the same bond lengths calculated at the B3LYP/6-31G(d,p) level of theory as reported earlier [
11]. Interestingly, the DFT method did not locate
4CO as a stationary point. Instead, repeated attempts at optimizing to the corresponding propellane led to ring opening to form bisketene
11 (
Figure 2). Note, however, that the bond length predicted when using the CCSD method for
4CO of 1.855 Å is exceptionally long, suggesting that
4CO as modeled using CCSD is not a true propellane structure to begin with, and likely occupies an unsustainable geometry. The same can be said for
4SO
2 for which CCSD predicted a bond length of 1.978 Å, and ωB97XD a bond length of 1.912 Å, both well out of the range of a possible legitimate C–C bond. On the whole, therefore, we were satisfied with the geometries predicted using the ωB97XD DFT functional in relation to those calculated using the CCSD method.
3.2. Optimization of Anionic Bridgehead Bromide Precursors
The geometries of the anionic bridgehead bromide compounds
12,
13, and
14 (see
Scheme 3) were optimized at the ωB97X-D/aug-cc-pVDZ level of theory. Note that, for those compounds with multiple N-H bonds or S-O bonds, the H/O atoms were oriented so as to be in a uniform clockwise direction. In addition, while we used NH bonds to simplify the calculations, an N-H bond would be incompatible with the formation of bridgehead anions, and the use of N-R derivatives would be more practical (e.g., R = Me). For all the compounds, optimization led either to ejection of the Br atom as a bromide ion and formation of the corresponding propellane, or simple optimization of the originally guessed geometry for the anionic bridgehead bromide compounds. In no cases were ring-opened or alternative products formed. If propellane formation did not occur, a frequency calculation was carried out on the optimized anionic bridgehead bromide compounds to ensure that it was a stationary point at an energy minimum. The results of these optimizations are compiled in column 3 of
Table 1. As representative examples of the outcomes of these optimizations, the result of the optimization of precursor
12O that led successfully to propellane
2O is shown in
Figure 3A, and the optimization of precursor
14O that did not result in the formation of propellane
4O, but only in the optimization of the geometry of
14O, is shown in
Figure 3B. A video showing the iterative steps involved in the optimization of precursor
12O to form
2O is provided in the
Supplementary Materials.
Several general observations may be made from the data in the table:
- (i)
In almost all cases, trisubstituted compounds 14 failed to generate the propellane 4, with the exception of 14NH.
- (ii)
In no cases were propellanes formed at substitution levels beyond those in which propellane formation failed (i.e., if propellane formation failed for 3, propellane formation also failed for 4).
- (iii)
The most resistant-to-form propellanes were those precursors substituted with CF2, CO, SO, and SO2 groups.
- (iv)
While there is no direct correlation between the bond length of the propellane central bond and whether the propellane formed or not, generally those with shorter bond distances (<1.66 Å) were more likely to successfully form, while those with longer bond distances (>1.66 Å) were resistant to forming.
For those anionic bridgehead bromide precursors that failed to form a propellane, we calculated the free energy change for the formation of the propellane from the corresponding anionic precursor. The results are provided in
Table 2. For most cases (
4O,
4S,
4CF
2,
3CO,
4SO,
3SO
2, and
4SO
2) the conversions are endergonic, which clearly explains the resistance to spontaneous formation of the propellane. However, for two of the cases (
3SO and
2SO
2), the conversions are exergonic. In these two cases, the lack of formation of the propellanes could possibly be attributed to the ability of these substituents to stabilize the negative charge on the precursor, thereby overcoming the energetic drive to form the corresponding propellanes.
From these observations, it would appear that anionic bridgehead bromides 12 and 13 substituted with O, NH, and S would be the most attractive synthetic targets with the highest likelihood of successfully forming the desired corresponding propellanes.
3.3. Estimating the Total Strain Energy in Propellanes 2–4
Pittman had utilized an isodesmic equation, represented by Equation (1) of
Figure 4, to estimate the total strain energies inherent in the trisubstituted propellanes
4 relative to unsubstituted
1 [
8]. We extended his method of calculating the strain energies for the mono and disubstituted derivatives
2 and
3 according to Equations (2) and (3). These calculated strain energies are provided in column 4 of
Table 1.
As can be seen in
Table 1, while there is reasonable agreement between the relative total strain energies calculated at the ωB97X-D versus the CCSD levels of theory, the DFT method consistently provided slightly higher strain energy estimates relative to CCSD theory. However, the general trend of the relative energies is retained, and groups may be partitioned into those with low (
4NH,
4S, and
4SO), medium (
4O), and high (
4CF
2,
4CO, and
4SO
2) levels of strain. Furthermore, there is generally observed to be an increase in the strain energy with each subsequent substitution of a CH
2 bridge as one progresses in the series from
2 to
4. For NH, S, and SO substitutions, the increase in the strain energy upon successive substitution is relatively small. This is especially true for NH substitutions in which the strain energy increases only marginally with increasing substitution. For O, the third substitution to form
4O dramatically increases the strain relative to
2O and
3O, but, overall, the strain is not very high. Particularly interesting, however, is the low strain energies predicted for the sulfoxide series. The propellane
2SO is predicted to be even less strained than unsubstituted
1, while
3SO and
4SO remain only marginally more strained. In contrast to those substituted series for which the strain is manageable, each addition of a CF
2, CO, or SO
2 group increases the strain energy dramatically.
As with the C-C bond distance of the final propellane structures, there is no obvious direct correlation of the probability of the successful formation of a propellane upon geometry optimization of an anionic bridgehead bromide with the total strain energy of the final propellane, although the propellane formation was generally favored when the total strain energy was less than 27 kcal/mol. However, several propellanes with strain energies below this level (e.g., 4S, 3SO, 4SO, and 2SO2) also failed to spontaneously form.
3.4. Estimating the Central Bridgehead-Bridgehead Bond Strain Energy in Propellanes 1–4
Given that the total strain energy of the final propellanes was not a conclusive indicator as to whether the propellane would form spontaneously upon the optimization of the anionic bridgehead bromide precursor, we wondered whether a better predictor would be the strain energy of the centrally formed bridgehead-bridgehead bond. Isodesmic Equations (4)–(6) (see
Figure 5) were developed to more directly isolate the strain experienced by the central propellane bonds of the derivatives relative to that of the unsubstituted propellane
1. The energies of the variously substituted bicyclopentanes found on the right side of these equations and the energy of the unsubstituted bicyclopentane found on the left side of these equations were calculated using the same optimization conditions as had been used for the propellanes. The resulting change in energy for each derivative was taken as an estimate of the strain energy localized at the bridgehead-bridgehead bond relative to that of
1. These calculated central bond strain energies are compiled in column 5 of
Table 1.
The trend in the strain energies of the central bonds calculated via isodesmic reactions (4)–(6) was identical to that calculated earlier on a subset of these compounds using the B3LYP/6-31G(d,p) method based on hydrogenation of the central bond of the propellane to form the corresponding bicyclopentane (see Equation (7) in
Figure 6) [
9,
11]. Both methods predict the order of stability of
1 >
2NH >
2S ~
3NH ~
2O >
4NH >
3O >
4O.
An interesting trend emerges when comparing the central bond energy strain (column 5,
Table 1) relative to the total strain energies (column 4,
Table 1). For those substituted propellanes that had overall lower total strain energies (O, NH, S, and SO), one notices that the strain of the central bond is generally higher than the total strain energy of the molecules. Hence, the central bond strain is compensated for by the substituents either structurally and/or electronically. However, for those propellanes that had higher total strain energies (CF
2, CO, and SO
2), their total strain energies are generally greater than that of the central bond strain energy. Hence, those substituents are unable to compensate for the strain introduced by the central bond and their bonding situation is apparently worsened either structurally and/or electronically. While it is certainly of interest as to what structural and/or electronic factors may be at play to either accommodate or exacerbate the strain energies of these molecules, this would require an in-depth analysis of the complex bonding situations [
2], which is beyond the scope of this current work.
The central bond strain energies were, therefore, also not direct predictors as to whether the propellane structure would form spontaneously upon geometry optimization of 12–14. While, generally, propellane formation occurred with compounds containing low central bond energy strain (i.e., <21 kcal/mol), in some cases, propellane formation failed to occur (e.g., for 4S, 3SO, 4SO, and 2SO2). However, in no cases were propellanes formed when the central bond strain energy exceeded 21 kcal/mol.
4. Conclusions
In many of the studied cases, geometry optimization of the anionic bridgehead bromide precursors spontaneously formed the corresponding propellane compounds. This suggests that for those compounds, the propellane is energetically favored relative to the precursor, and has a higher likelihood of forming the propellane experimentally. It should be noted, however, that for those anionic bridgehead bromides that did not spontaneously form propellanes, it is not impossible that they could also successfully form propellanes under the proper conditions. It may be that those bromides have an energetic barrier toward the formation of the propellanes, and, when provided that energy, may be able to surmount that barrier and form the desired propellanes. However, in our quest to locate the most promising propellane targets, we prioritize the anionic bridgehead bromides that form the propellanes spontaneously upon optimization. Combining the results of the optimizations with what was learned from the analysis of the lengths of the central propellane bonds and the strain energies (both total strain energies and those of the central bond), it would appear that the most promising synthetic targets using the synthetic method outlined in
Scheme 1 would be those propellanes that:
- (i)
Successfully formed the corresponding propellane upon geometry optimization of precursors 12–14.
- (ii)
Form propellanes that have central bridgehead-bridgehead bond lengths <1.66 Å.
- (iii)
Have low total strain energies (i.e., <27 kcal/mol).
- (iv)
Have low central C-C bond energies (i.e., <21 kcal/mol).
The most synthetically attractive propellanes, therefore, would be compounds 2O, 2NH, 3NH, 4NH, 2S, and 3S. Compounds 2CF2, 2CO, and 2SO are also possible contenders, but the behavior of their more highly substituted counterparts render them more suspect than the former recommendations. We hope that the results from this study stimulate synthetic chemists to consider ways in which to synthesize the precursor compounds for further experimental investigations.