Next Article in Journal
Silica In Silico: A Molecular Dynamics Characterization of the Early Stages of Protein Embedding for Atom Probe Tomography
Next Article in Special Issue
Decomposition of Small Molecules for Fragment-Based Drug Design
Previous Article in Journal
Computational Modeling of the Interaction of Molecular Oxygen with the miniSOG Protein—A Light Induced Source of Singlet Oxygen
Previous Article in Special Issue
Structural Analysis of Interactions between Epidermal Growth Factor Receptor (EGFR) Mutants and Their Inhibitors
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Biophysica
Volume 3
Issue 2
10.3390/biophysica3020017
biophysica-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Coarse-Grained MD Simulations of Opioid Interactions with the μ-Opioid Receptor and the Surrounding Lipid Membrane

by
Sourav Ray
1,
Konstantin Fackeldey
1,2,*,
Christoph Stein
3 and
Marcus Weber
1
1
Zuse Institute Berlin (ZIB),Takustrasse 7, 14195 Berlin, Germany
2
TU Berlin, Institute for Mathematics, Strasse des 17. Juni 135, 10623 Berlin, Germany
3
Institute of Experimental Anaesthesiology, Charité Universitätsmedizin Berlin, 12200 Berlin, Germany
*
Author to whom correspondence should be addressed.
Biophysica 2023, 3(2), 263-275; https://doi.org/10.3390/biophysica3020017
Submission received: 23 January 2023 / Revised: 21 March 2023 / Accepted: 3 April 2023 / Published: 6 April 2023
(This article belongs to the Special Issue Molecular Structure and Simulation in Biological System)
Browse Figures
Versions Notes

Abstract

:
In our previous studies, a new opioid (NFEPP) was developed to only selectively bind to the μ -opoid receptor (MOR) in inflamed tissue and thus avoid the severe side effects of fentanyl. We know that NFEPP has a reduced binding affinity to MOR in healthy tissue. Inspired by the modelling and simulations performed by Sutcliffe et al., we present our own results of coarse-grained molecular dynamics simulations of fentanyl and NFEPP with regards to their interaction with the μ -opioid receptor embedded within the lipid cell membrane. For technical reasons, we have slightly modified Sutcliffe’s parametrisation of opioids. The pH-dependent opioid simulations are of interest because while fentanyl is protonated at the physiological pH, NFEPP is deprotonated due to its lower pKa value than that of fentanyl. Here, we analyse for the first time whether pH changes have an effect on the dynamical behaviour of NFEPP when it is inside the cell membrane. Besides these changes, our analysis shows a possible alternative interaction of NFEPP at pH 7.4 outside the binding region of the MOR. The interaction potential of NFEPP with MOR is also depicted by analysing the provided statistical molecular dynamics simulations with the aid of an eigenvector analysis of a transition rate matrix. In our modelling, we see differences in the XY-diffusion profiles of NFEPP compared with fentanyl in the cell membrane.

Graphical Abstract

1. Introduction

Clinically used opioids, such as morphine or fentanyl, are powerful pain killers, but they also have unwanted and even lethal side effects. The suppression of pain is mediated by these opioid ligands binding to and activating μ -opioid receptors (MOR), which are located on central and peripheral neurons. One possible way to reduce side effects is ensuring that the opioids only activate MOR in the periphery and not centrally (in the brain). Here, one can take advantage of the fact that pain usually goes hand in hand with inflammation in injured tissue. Inflammation lowers the pH value and leads to an acidic chemical environment.
Recent work by our group [1] led to the development of the novel analgesic compound N-(3-fluoro-1-phenethylpiperidin-4-yl)-N-phenylpropionamide (NFEPP), which activates MOR preferentially at acidic extracellular pH levels, as found in injured tissues [2]. Apparently, the low pKa of NFEPP (6.82 [1,3]) precludes its protonation in healthy tissues (pH >7.35; e.g., in the brain) but facilitates its protonation in injured/inflamed microenvironments (low pH, high concentrations of protons). Consistent with the notion that the protonation of opioid ligands is typically required for their binding to opioid receptors [4], NFEPP is active only in injured tissues, while at physiological pH in healthy tissues (e.g., brain), NFEPP deprotonates and loses its ability to bind to MOR. In contrast, the closely related conventional opioid fentanyl (pKa = 8.43 [3,5]) is protonated and able to activate MOR at both low and normal pH, and therefore produces both analgesic effects and central side effects.
Aside from pH, other inflammatory mediators also play important roles. For example, proinflammatory peptides and reactive oxygen species (radicals) can be associated with the formation of disulfide bonds (DSBs), which may modulate the function of G-protein coupled receptors (GPCRs) [6,7,8,9]. In addition, the micropharmacokinetics of ligands penetrating into neuronal membranes should be considered.
A recent study [10] examined the interaction of fentanyl with MOR embedded in a lipid bilayer using coarse-grained (CG) molecular dynamics (MD) simulations. With fully atomistic (FA) simulations, time scales of milliseconds or higher are usually required to observe rare events such as ligand binding. CG force fields combine groups of atoms into interaction sites or beads and thereby diminish the computational costs compared with simulations with FA force fields [11]. Hence, CG MD simulations were employed to deal with such sampling issues by attaining significant computational acceleration relative to FA MD simulations [10,11].
It was earlier noted that fentanyl demonstrates high lipid solubility, and thus, has a tendency to partition into the lipid bilayer without passing through the entire membrane [10]. In the present work, we tweaked the ligand modelling as per the FA atom to CG bead mapping MARTINI 2.0 guidelines [12]. Therefore, the Nd and Qd beads used in the previous study have been substituted with N0 and Q0 beads, respectively. Here, the N (nonpolar) and Q (charged) bead types correspond to particular beads used in the CG representation of deprotonated and protonated ligands, respectively. Furthermore, the suffixes d and 0 denote donor and none hydrogen-bonding abilities, respectively.
Such a modification of the ligand mapping would also alter the intramolecular, as well as intermolecular, interaction of these ligands in the CG system models. Hence, incorporating this modified modelling, the role of pH and the presence of an additional DSB within the MOR were investigated by modelling different scenarios. Afterwards, the interaction of these ligands with the membrane-embedded MOR was studied with the help of CG MD simulations.

2. Models and Methods

2.1. Fully Atomistic Molecular Dynamics Simulations

In the the FA and CG MD simulations, the difference between inflamed and healthy tissues was modelled by changes in pH and with the formation of a DSB [6]. The protonation states of the different amino acid residues of the MOR were determined using the PROPKA predictor tool [13,14] with respect to the system acidity values of pH 6.5 and pH 7.4, corresponding to the inflamed and healthy system states, respectively.
For molecular modelling, the mouse MOR structure was procured from the RCSB database (Protein Data Bank (PDB) [15]: 6DDF [16]). Interestingly, in the Gi-stabilised active states of MOR, the TM6 helix of the MOR is displaced towards the TM7 helix [16]. Furthermore, a recent in silico study has identified the preferential TM6 and TM7 conformational changes in the course of fentanyl-induced MOR activation [17]. Hence, in the mouse MOR, CYS 2926.47 of the TM6 helix and CYS 3217.38 of the neighbouring TM7 helix were selected for the introduction of an additional DSB at pH 6.5 to model the effect of reactive oxygen species on the MOR within inflamed tissues [6,7,8,9]. Sulfur atoms of these two cysteine residues are at a distance of 0.987 nm in the native mouse MOR crystal structure [16]. Thus, the dynamics of the MOR were examined with and without an additional CYS 2926.47 − CYS 3217.38 DSB (for terminology, please refer to [18]) in the receptor at pH 6.5 and pH 7.4, respectively.
The receptors were inserted into the POPC (1-palmitoyl-2-oleoyl-sn- glycero-3-phosphocholine) bilayer models using the CHARMM-GUI Membrane Builder [19]. Similarly to [3], MD simulations were performed with GROMACS 2019.6 [20], using the CHARMM36m force field for the ligands [21], receptor [22] and lipids [23]. As an explicit solvent, the CHARMM TIP3P water model [24] was used. Sodium and chloride counterions were added to neutralise the excess charge and obtain a salt concentration of 0.15 M. All simulation systems went through consecutive minimisation, equilibration and production runs, using the GROMACS scripts generated by CHARMM-GUI [19]. First, the systems were energy minimised with steepest descent algorithms, followed by six-step equilibration runs. The first two runs were performed in the NVT (constant particle number, volume, and temperature) ensemble and the remaining runs in the NPT (constant particle number, pressure, and temperature) ensemble. Restraint forces were applied to the receptor, lipids, and water molecules, and Z-axis positional restraints were placed on lipid atoms to restrict their motion along the X-Y plane. These restraints were progressively reduced during the equilibration process. Ultimately, unrestrained NPT production runs of 1 μs were performed, with periodic boundary conditions along all three orthonormal directions.
The particle mesh Ewald (PME) method [25] was employed to calculate long-range Coulombic interactions, with a 1.2 nm cut-off for real-space interactions. A force-switch function was implemented for the Lennard–Jones interactions, with a smooth cut-off from 1.0 to 1.2 nm. The temperature was maintained at 310 K using the Nosé–Hoover thermostat [26,27]. System pressure was kept at 1 bar with the Parrinello–Rahman barostat [28], using a semi-isotropic scheme where pressures along the X-Y-directions and the Z-direction were coupled separately. The coupling constant and compressibility of the barostat were set to 5 ps and 4.5 × 10 − 5 bar, respectively. The LINCS algorithm [29] was used to constrain the covalent bonds between hydrogen and other heavy atoms, allowing a simulation time step of 2 fs. Production run trajectories were saved every 1 ns, and processed with GROMACS analysis tools to generate the required information. VMD software [30] was used for visualisation.
The protonated form of fentanyl, and the protonated and deprotonated forms of NFEPP [1], were sketched and parameterised using the CHARMM-GUI Ligand Reader & Modeler [31]. To parameterise these ligands in MARTINI, initially, 1 μ s FA MD simulations of a single ligand in TIP3P water and 0.15 M NaCl were conducted using the CHARMM36m force field [10]. System pressure was maintained at 1 bar with the Parrinello–Rahman barostat using an isotropic scheme, where pressures along all three orthonormal directions were coupled together. The rest of the simulation parameters were kept similar to those described earlier for the MD simulations of MOR embedded in POPC bilayer.

2.2. Coarse-Grained Molecular Dynamics Simulations

The protein structure coordinates of the mouse MOR structure (PDB: 6DDF) were converted to CG MARTINI 2.2 representation [32] using Martinize2 [12,32,33,34,35]. An additional CYS 2926.47− CYS 3217.38 DSB was incorporated into the MOR at pH 6.5, as mentioned earlier for the FA simulations. The ElNeDyn elastic network [35] with a spring force constant of 500 kJ · mol − 1 · nm − 2 and a cutoff of 0.9 nm was applied to the CG protein structure [36]. The FA ligand trajectories were extracted from the single ligand simulations. Atom-to-bead mapping of the ligands was performed with the CG Builder tool [37], and as shown in Figure 1a,b, each atom in the FA representation of the ligand was assigned to an appropriate CG bead [12]. The CG ligand parametrisation was performed using the Bartender program [38,39,40,41], with the FA ligand trajectories supplied as reference. A temperature value of 310 K and a system dielectric value of 74.21 [42] were provided during the parametrisation.
The CG MOR was then embedded in a membrane bilayer with a lipid composition, as listed in Table 1 [12,36,43,44,45,46,47,48,49,50], using the insane script [44]. The average areas per phospholipid were set to 0.59 nm 2 and 0.55 nm 2 for the inner and the outer leaflets, respectively [51]. The initial size of the system box was maintained as 10.0 × 10.0 × 12.5 nm 3 . The MOR–bilayer complex was afterwards solvated in polarisable water [34] with 0.15 M NaCl. For the simulations with opioid ligands, 4 molecules of the ligand were then added to the system using the PACKMOL package [52]. In Figure 1c, a snapshot of the initial state of a CG system setup before the MD simulation is presented, consisting of four deprotonated NFEPP molecules along with the MOR at pH 7.4. The CG MD simulations were performed using the MARTINI 2.3P force field [53]. The systems were first energy minimised over 50,000 steps using the steepest descent algorithm, then equilibrated with NVT ensemble and then NPT ensembles for a total duration of 10 ns. Constraints were applied to the MOR and were progressively reduced during the equilibration process. Subsequently, production simulations with a 20 fs timestep were performed in NPT ensembles for 5 μ s.
The temperature was set to 310 K and maintained using the V-rescale thermostat [54]. The pressure was set to 1 bar and maintained using the Parrinello–Rahman barostat. Semi-isotropic pressure coupling was applied for these systems, with pressure along the X-Y-directions and the Z-direction coupled separately. The barostat coupling constant and compressibility were set to 12 ps and 3 × 10 − 4 bar, respectively. For calculation of nonbonded interactions, a pair list was generated using the Verlet scheme with a buffer tolerance of 0.005. The Coulombic terms were calculated using PME and a real-space cutoff of 1.1 nm [55]. The relative dielectric constant was set to 2.5, as recommended for the polarizable water model [34]. For the VDW terms, a cutoff scheme with a cutoff value of 1.1 nm was employed along with the Verlet cutoff scheme for the potential-shift. The LINCS algorithm was implemented to constrain the bonds to their equilibration values. The simulation trajectories were analysed using the GROMACS analysis tools and MATLAB software [56]. The trajectory visualisation was performed in VMD.

2.3. Square Root Approximation

The trajectories generated a sequence of states. Due to the large amount of data and the high-dimensional structure of the state space, besides a direct analysis of the states, we also aim to carry out an analysis of the distribution of opioids in the membrane. Therefore, we aim to describe the ligand transitions inside the membrane by a rate matrix Q, giving the kinetics between collections of dynamically similar states. The states generated by the trajectory are Boltzmann distributed, and thus, dynamically similar states are adjacent. For assembling the matrix Q, we decompose the state space into Voronoi cells ( ω i ) i = 1 , . . . , n such that each of the Voronoi cells has at least one of the states in it. In the next step, we count the number of states w i in each Voronoi cell ω i . For neighbouring cells, the entries Q i j of the rate matrix Q are then computed by
Q i j = w j w i .
This method, which is based on a cascade of approximations of the actual transition rates, is called square-root-approximation (SqrA) [57,58,59].

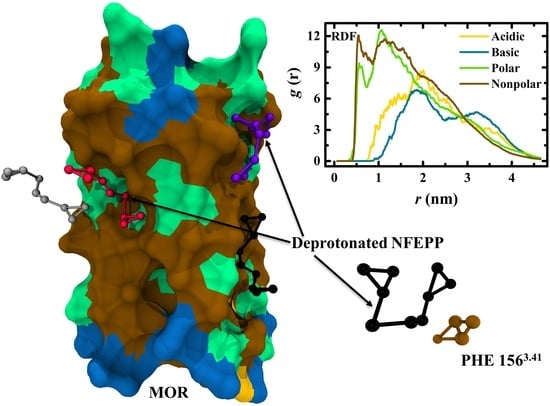
3. Results

The distance between the TM6 and TM7 helices of the membrane-bound MOR was tracked across the FA and CG simulations without any ligand molecule. In Figure 2c,d, it could be observed that the distances between the helices fluctuate by up to 0.2 nm over the simulation period. However, the pH 6.5 systems with an additional CYS 2926.47 − CYS 3217.38 DSB (Figure 2b) had the helices in a greater proximity compared with pH 7.4 systems without an additional DSB (Figure 2a). Significantly, this trend was found to be similar in both FA and CG simulations.
Thus, the CG models were able to exhibit similar characteristics, as noted in the corresponding FA simulations. Hence, to access faster time scales, CG models of membrane-embedded MOR were analysed with MD simulations. Furthermore, the interaction of ligand molecules with the surrounding environment was also studied using CG modelling.
The spatial distributions of ligand molecules with regard to the receptor are depicted in Figure 3. Each cross corresponds to a ligand position in consecutive time steps of the MD simulation. In Figure 3a,b, we map the XY-distribution at pH 6.5 compared with pH 7.4. The Z direction histogram is shown in Figure 3c. In contrast to the opioids which are activating the MOR, the non-active NFEPP at pH 7.4 enters the membrane more deeply (blue line). This results in less availability of NFEPP at the membrane surface at pH 7.4. After examining the data presented in Figure 3, we decided to explore the interaction between the NFEPP molecules and the MOR at pH 7 in greater detail. Several distances were calculated between these two groups to elicit further information, as depicted in Figure 4. From the distances across the XY plane between the NFEPP molecules and the MOR in Figure 4a, no significant trends could be observed. Therefore, we decided to analyse the movement of ligands along the Z axis, to check their movement across the simulation system. For this purpose, the Z axis values of the centre of mass coordinates were subtracted from the commensurate values of the NFEPP molecules. Although not much could be inferred from these calculations for three out of the four ligands shown in Figure 4b, the remaining ligand, henceforth referred to as “Ligand 1”, was able to transport to a region below the centre of mass of the MOR. As the central portion of the MOR is embedded within the lipid bilayer, this indicated the entry of Ligand 1 into the bilayer region. Encouraged by this observation, we decided to calculate the minimum interatomic distances between the NFEPP molecules and the MOR. Based on the data from Figure 4c, we decided to calculate the radial distribution functions between Ligand 1 and the different residue groups of the MOR for the last 250 ns of the corresponding simulation trajectory. During this time frame, not only is Ligand 1 in close proximity to the MOR, but it is also present within the membrane bilayer region of the system.
From the trajectory snapshot depicting the interaction of NFEPP molecules with the MOR at pH 7 in Figure 5a, it was observed that, apart from Ligand 1, other ligands were in the vicinity of the upper leaflet of the membrane bilayer. Only Ligand 1, which was able to cross the solvent–membrane interface as previously noted in Figure 4b, appears to be closer to the lower leaflet than the upper leaflet of the bilayer. Afterwards, the same trajectory frame is displayed in Figure 5b, with the amino acid residues on the MOR surface categorised into four types based on their steric and Coulombic properties: acidic (negatively charged: Asp, Glu), basic (positively charged: Arg, Lys), nonpolar (neutral: Ala, Gly, Ile, Leu, Met, Phe, Pro, Trp and Val) and polar (neutral: Asn, Cys, Gln, Ser, Thr, Tyr, deprotonated His and protonated Asp) [30,60]. From this trajectory snapshot, it could be observed that deprotonated NFEPP prefers interaction with both the nonpolar and polar amino acid residues on the membrane-embedded region of the MOR surface. It shows relatively diminished interaction with the acidic and basic surface residues, primarily located at the solvent-accessible extremities of the MOR. Similar trends could be observed in Figure 5c, where radial distribution functions were calculated between Ligand 1 and these four residue groups. Significantly, once inside the membrane bilayer, the deprotonated NFEPP was found to demonstrate a stable interaction with the amphiphilic MOR surface, as opposed to a lipophilic interaction with the lipid bilayer tails. Furthermore, upon analyzing the interaction between Ligand 1 and the MOR in greater detail, it was observed that interaction with the residue PHE 1563.41 in the TM3 helix of membrane-embedded MOR surface played an important role in stabilizing the interaction between Ligand 1 and MOR, as depicted in Figure 5d.
It is not easy to quantify the differences between the distributions of the ligands from Figure 3a,b. In order to make these differences more visible, we divided the XY-direction of the membrane into equally sized cells and used SqrA in order to derive the diffusion profile of the ligands by generating a rate matrix Q of the process; see Figure 6. The term “diffusion profile” refers to the fact that the SqrA is basically a discretised Fokker–Planck diffusion operator [61]. For the SqrA, the correspondence between eigenvalues and time scales has been discussed [62]. In this sense, the graphs Figure 6a–d represent the χ -function of the slowest process, i.e., the gradient of this function points in the direction of the slowest processes. Compared with the diffusion profile of a ligand, which does not interact with the receptor Figure 6e, the χ -function of the NFEPP molecule at pH 6.5 and at pH 7.4 has a very different profile. It has two plateaus (metastable states) instead of four. The fentanyl molecule shows a kind of χ -function that is more like a free diffusion. This too shows that NFEPP has a higher tendency to interact with the MOR when moving inside the membrane. The second highest eigenvalue of the diffusion rate matrix corresponds to the characteristic time scale of the movement [62]. Again in Figure 6f, the biggest difference is between NFEPP at pH 6.5 and NFEPP at pH 7.4. Thus, the protonation state of NFEPP seems to have a substantial impact on its dynamical behaviour within the membrane.

4. Discussion

As coarse-graining combines three to four, or sometimes more, heavy atoms and their associated hydrogen atoms into a single bead [12], the fentanyl CG models employed in this study could also be applicable to opioid molecules with a chemical structure similar to fentanyl [10]. The same could be said for NFEPP and the halogenated fentanyl derivatives with a structure close to NFEPP. Furthermore, an improved CG modelling scheme and force field MARTINI 3.0 is currently available, with reportedly better representation of intrapeptide and interpeptide interactions along with protein-lipid interactions [63]. Additionally, an enhanced scheme for modelling small molecules, such as fentanyl and NFEPP, has been recently developed for this force field [64]. However, at present, the MARTINI 3.0 parameters for Chol, DPG3, DPSM and POP2 are not available [10,36,65]. Therefore, it was decided to use the MARTINI 2.2 and MARTINI 2.0 modelling schematics for the MOR and ligands, respectively, along with the MARTINI 2.3P force field.
The present study aimed to shed some light on the generic interaction of fentanyl and NFEPP opioid molecules with MOR and the lipid bilayer as a function of the surrounding physicochemical microenvironment. To access greater time scales, CG simulations were performed. It was observed that charged ligand molecules were unable to penetrate into the lipid bilayer. However, the deprotonated or neutral NFEPP at pH 7 was able to enter the membrane after crossing the membrane head group–lipid tail interface. However, upon forming a stable contact with the amphiphilic region of the MOR surface embedded within the bilayer, the ligand molecule preferred interaction with the MOR surface, instead of returning back to the hydrophobic environment in the midst of the lipid tail segments. Such amphiphilic behaviour has been also observed for deprotonated fentanyl in a recent FA MD simulation study, where a fentanyl molecule, initially placed between the tail segments of lipid molecules of the bilayer, was able to reach the membrane–solvent surface and interact with the solvent water molecules by reorienting itself within the membrane bilayer [66]. Furthermore, similar association of a BPTU ligand from the solvent region to the membrane-embedded region of a G-protein coupled receptor via the membrane bilayer has also been observed [67].
The pH-dependent membrane absorption of ligand molecules has been reported earlier [68,69], where ligands demonstrated increased surface uptake with increasing extracellular pH values, especially at pH greater than the ligand’s pKa values. However, more recent in vivo studies are required to further corroborate these findings. Significantly, fluorinated analogues of fentanyl with a similar pKa were found to exhibit equivalent behaviour in vivo [70,71]. However, NFEPP and other fluorinated analogues, with pKa values lower than the physiological pH of 7.4, were found to exhibit highly pH-dependent biological activity near their pKa values, similar to the behaviour demonstrated by NFEPP in the current study. Therefore, the localisation of deprotonated NFEPP molecules near the MOR surface after entering via the lipid bilayer could diminish its bio-availability in the extracellular environment, which might also reduce its likelihood to interact with the MOR binding region and trigger its subsequent activation [3].
It is already known that NFEPP and fentanyl at pH 7.4 behave differently with regard to receptor activation. It has also been shown that NFEPP at pH 7.4 and NFEPP at pH 6.5 have different activation profiles [1]. However, the differences between fentanyl and NFEPP at pH 6.5 have rarely been analysed using molecular simulation methods in the literature. Our novel observations suggest that, besides the binding affinities, there might be more general differences between fentanyl and NFEPP with regard to interaction with the cell membrane. The fluorine atom of NFEPP increases the amphiphilic character of fentanyl. The process of approaching and binding to the MOR could also be different for fentanyl and NFEPP at pH 6.5, which has not been taken into account in pre-clinical studies so far, but is visible by comparing Figure 6a with Figure 6c.

Author Contributions

Conceptualisation: M.W., C.S. Method selection/description: S.R., M.W., K.F. Formal analysis: S.R., M.W., K.F. Clinical aspects of results/discussions: C.S. Investigation: S.R. Supervision: M.W. Writing: all authors. All authors have read and agreed to the published version of the manuscript.

Funding

This research was partially funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy—The Berlin Mathematics Research Center MATH+ (EXC-2046/1 project ID: 390685689).

Data Availability Statement

Code and data are available at https://github.com/user8490/opioid.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Spahn, V.; Del-Vecchio, G.; Labuz, D.; Rodriguez-Gaztelumendi, A.; Massaly, N.; Temp, J.; Stein, C. A nontoxic pain killer designed by modeling of pathological receptor conformations. Science 2017, 355, 966–969. [Google Scholar] [CrossRef] [PubMed]
  2. Stein, C. New concepts in opioid analgesia. Expert Opin. Investig. Drugs 2018, 27, 765–775. [Google Scholar] [CrossRef]
  3. Ray, S.; Sunkara, V.; Schütte, C.; Weber, M. How to calculate pH-dependent binding rates for receptor-ligand systems based on thermodynamic simulations with different binding motifs. Mol. Simul. 2020, 46, 1443–1452. [Google Scholar] [CrossRef]
  4. Lešnik, S.; Bertalan, E.; Bren, U.; Bondar, A.N. Opioid Receptors and Protonation-Coupled Binding of Opioid Drugs. Int. J. Mol. Sci. 2021, 22, 13353. [Google Scholar] [CrossRef] [PubMed]
  5. Settimo, L.; Bellman, K.; Knegtel, R.M.A. Comparison of the Accuracy of Experimental and Predicted pKa Values of Basic and Acidic Compounds. Pharm. Res. 2014, 31, 1082–1095. [Google Scholar] [CrossRef] [PubMed]
  6. Bowen, W.D.; Pert, C.B. Conformational malleability of opiate receptors: Sulfhydryl modification alters ion-induced μ/δ-ligand selectivity shifts in rat striatal sections. Cell. Mol. Neurobiol. 1982, 2, 115–128. [Google Scholar] [CrossRef]
  7. Yang, F.; Guo, L.; Li, Y.; Wang, G.; Wang, J.; Zhang, C.; Sun, J.P. Structure, function and pharmacology of human itch receptor complexes. Nature 2021, 600, 164–169. [Google Scholar] [CrossRef] [PubMed]
  8. Cao, C.; Kang, H.J.; Singh, I.; Chen, H.; Zhang, C.; Ye, W.; Roth, B.L. Structure, function and pharmacology of human itch GPCRs. Nature 2021, 600, 170–175. [Google Scholar] [CrossRef] [PubMed]
  9. Cremers, C.M.; Jakob, U. Oxidant sensing by reversible disulfide bond formation. J. Biol. Chem. 2013, 288, 26489–26496. [Google Scholar] [CrossRef] [Green Version]
  10. Sutcliffe, K.J.; Corey, R.A.; Alhosan, N.; Cavallo, D.; Groom, S.; Santiago, M.; Kely, E. Interaction With the Lipid Membrane Influences Fentanyl Pharmacology. Adv. Drug Alcohol Res. 2022, 2, 10280. [Google Scholar] [CrossRef]
  11. Souza, P.C.T.; Thallmair, S.; Conflitti, P.; Ram írez Palacios, C.; Alessandri, R.; Raniolo, S.; Marrink, S.J. Protein—ligand binding with the coarse-grained Martini model. Nat. Commun. 2020, 11, 3714. [Google Scholar] [CrossRef]
  12. Marrink, S.J.; Risselada, H.J.; Yefimov, S.; Tieleman, D.P.; de Vries, A.H. The MARTINI Force Field: Coarse Grained Model for Biomolecular Simulations. J. Phys. Chem. B 2007, 111, 7812–7824. [Google Scholar] [CrossRef] [Green Version]
  13. Olsson, M.H.M.; Søndergaard, C.R.; Rostkowski, M.; Jensen, J.H. PROPKA3: Consistent Treatment of Internal and Surface Residues in Empirical pKa Predictions. J. Chem. Theory Comput. 2011, 7, 525–537. [Google Scholar] [CrossRef] [PubMed]
  14. Søndergaard, C.R.; Olsson, M.H.M.; Rostkowski, M.; Jensen, J.H. Improved Treatment of Ligands and Coupling Effects in Empirical Calculation and Rationalization of pKa Values. J. Chem. Theory Comput. 2011, 7, 2284–2295. [Google Scholar] [CrossRef] [PubMed]
  15. wwPDB Consortium. Protein Data Bank: The single global archive for 3D macromolecular structure data. Nucleic Acids Res. 2019, 47, D520–D528. [Google Scholar] [CrossRef] [Green Version]
  16. Koehl, A.; Hu, H.; Maeda, S.; Zhang, Y.; Qu, Q.; Paggi, J.M.; Xu, H.E. Structure of the μ-opioid receptor-G-protein complex. Nature 2018, 558, 547–552. [Google Scholar] [CrossRef] [PubMed]
  17. Ricarte, A.; Dalton, J.A.R.; Giraldo, J. Structural Assessment of Agonist Efficacy in the μ-Opioid Receptor: Morphine and Fentanyl Elicit Different Activation Patterns. J. Chem. Inf. Model. 2021, 61, 1251–1274. [Google Scholar] [CrossRef]
  18. Isberg, V.; de Graaf, C.; Bortolato, A.; Cherezov, V.; Katritch, V.; Marshall, F.H.; Mordalski, S.; Pin, J.-P.; Stevens, R.C.; Vriend, G.; et al. Generic GPCR residue numbers—Aligning topology maps while minding the gaps. Trends Pharmacol. Sci. 2015, 36, 22–31. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  19. Lee, J.; Patel, D.S.; Ståhle, J.; Park, S.J.; Kern, N.B.; Kim, S.; Lee, J.; Cheng, X.; Valvano, M.A.; Holst, O.; et al. CHARMM-GUI Membrane Builder for Complex Biological Membrane Simulations with Glycolipids and Lipoglycans. J. Chem. Theory Comput. 2019, 15, 775–786. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  20. Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1, 19–25. [Google Scholar] [CrossRef] [Green Version]
  21. Gutiérrez, I.S.; Lin, F.Y.; Vanommeslaeghe, K.; Lemkul, J.A.; Armacost, K.A.; Brooks, C.L.; MacKerell, A.D. Parametrization of halogen bonds in the CHARMM general force field: Improved treatment of ligand-protein interactions. Bioorganic Med. Chem. 2016, 24, 4812–4825. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  22. Huang, J.; Rauscher, S.; Nawrocki, G.; Ran, T.; Feig, M.; de Groot, B.L.; Grubmüller, H.; MacKerell, A.D., Jr. CHARMM36m: An improved force field for folded and intrinsically disordered proteins. Nat. Methods 2017, 14, 71–73. [Google Scholar] [CrossRef] [Green Version]
  23. Klauda, J.B.; Venable, R.M.; Freites, J.A.; O’Connor, J.W.; Tobias, D.J.; Mondragon-Ramirez, C.; Vorobyov, I.; MacKerell, A.D., Jr.; Pastor, R.W. Update of the CHARMM All-Atom Additive Force Field for Lipids: Validation on Six Lipid Types. J. Phys. Chem. B 2010, 114, 7830–7843. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  24. Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
  25. Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef] [Green Version]
  26. Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
  27. Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  28. Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
  29. Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
  30. Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
  31. Kim, S.; Lee, J.; Jo, S.; Brooks, I.; Charles, L.; Lee, H.S.; Im, W. CHARMM-GUI ligand reader and modeler for CHARMM force field generation of small molecules. J. Comput. Chem. 2017, 38, 1879–1886. [Google Scholar] [CrossRef]
  32. De Jong, D.H.; Singh, G.; Bennett, W.F.D.; Arnarez, C.; Wassenaar, T.A.; Schäfer, L.V.; Periole, X.; Tieleman, D.P.; Marrink, S.J. Improved Parameters for the Martini Coarse-Grained Protein Force Field. J. Chem. Theory Comput. 2013, 9, 687–697. [Google Scholar] [CrossRef]
  33. Monticelli, L.; Kandasamy, S.K.; Periole, X.; Larson, R.G.; Tieleman, D.P.; Marrink, S.J. The MARTINI Coarse-Grained Force Field: Extension to Proteins. J. Chem. Theory Comput. 2008, 4, 819–834. [Google Scholar] [CrossRef] [PubMed]
  34. Yesylevskyy, S.O.; Schäfer, L.V.; Sengupta, D.; Marrink, S.J. Polarizable Water Model for the Coarse-Grained MARTINI Force Field. PLoS Comput. Biol. 2010, 6, e810. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  35. Periole, X.; Cavalli, M.; Marrink, S.J.; Ceruso, M.A. Combining an Elastic Network With a Coarse-Grained Molecular Force Field: Structure, Dynamics, and Intermolecular Recognition. J. Chem. Theory Comput. 2009, 5, 2531–2543. [Google Scholar] [CrossRef] [Green Version]
  36. Ansell, T.B.; Song, W.; Sansom, M.S.P. The Glycosphingolipid GM3 Modulates Conformational Dynamics of the Glucagon Receptor. Biophys. J. 2020, 119, 300–313. [Google Scholar] [CrossRef]
  37. Barnoud, J. CG Builder. Available online: https://jbarnoud.github.io/cgbuilder/ (accessed on 25 September 2021).
  38. Bannwarth, C.; Caldeweyher, E.; Ehlert, S.; Hansen, A.; Pracht, P.; Seibert, J.; Spicher, S.; Grimme, S. Extended tight-binding quantum chemistry methods. WIREs Comput. Mol. Sci. 2021, 11, e1493. [Google Scholar] [CrossRef]
  39. Ehlert, S.; Stahn, M.; Spicher, S.; Grimme, S. Robust and Efficient Implicit Solvation Model for Fast Semiempirical Methods. J. Chem. Theory Comput. 2021, 17, 4250–4261. [Google Scholar] [CrossRef] [PubMed]
  40. Bannwarth, C.; Ehlert, S.; Grimme, S. GFN2-xTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions. J. Chem. Theory Comput. 2019, 15, 1652–1671. [Google Scholar] [CrossRef] [Green Version]
  41. Spicher, S.; Grimme, S. Robust Atomistic Modeling of Materials, Organometallic, and Biochemical Systems. Angew. Chem. Int. Ed. 2020, 59, 15665–15673. [Google Scholar] [CrossRef]
  42. Zhou, J.; Rao, X.; Liu, X.; Li, T.; Zhou, L.; Zheng, Y.; Zhu, Z. Temperature dependent optical and dielectric properties of liquid water studied by terahertz time-domain spectroscopy. AIP Adv. 2019, 9, 035346. [Google Scholar] [CrossRef] [Green Version]
  43. Marrink, S.J.; de Vries, A.H.; Mark, A.E. Coarse Grained Model for Semiquantitative Lipid Simulations. J. Phys. Chem. B 2004, 108, 750–760. [Google Scholar] [CrossRef] [Green Version]
  44. Wassenaar, T.A.; Ingólfsson, H.I.; Böckmann, R.A.; Tieleman, D.P.; Marrink, S.J. Computational Lipidomics with insane: A Versatile Tool for Generating Custom Membranes for Molecular Simulations. J. Chem. Theory Comput. 2015, 11, 2144–2155. [Google Scholar] [CrossRef] [PubMed]
  45. Ingólfsson, H.I.; Melo, M.N.; van Eerden, F.J.; Arnarez, C.; Lopez, C.A.; Wassenaar, T.A.; Periole, X.; de Vries, A.H.; Tieleman, D.P.; Marrink, S.J. Lipid Organization of the Plasma Membrane. J. Am. Chem. Soc. 2014, 136, 14554–14559. [Google Scholar] [CrossRef] [PubMed]
  46. Baoukina, S.; Monticelli, L.; Risselada, H.J.; Marrink, S.J.; Tieleman, D.P. The molecular mechanism of lipid monolayer collapse. Proc. Natl. Acad. Sci. USA 2008, 105, 10803–10808. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  47. López, C.A.; Sovova, Z.; van Eerden, F.J.; de Vries, A.H.; Marrink, S.J. Martini Force Field Parameters for Glycolipids. J. Chem. Theory Comput. 2013, 9, 1694–1708. [Google Scholar] [CrossRef] [Green Version]
  48. Gu, R.X.; Ingólfsson, H.I.; deVries, A.H.; Marrink, S.J.; Tieleman, D.P. Ganglioside-Lipid and Ganglioside-Protein Interactions Revealed by Coarse-Grained and Atomistic Molecular Dynamics Simulations. J. Phys. Chem. B 2017, 121, 3262–3275. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  49. Marrink, S.J.; de Vries, A.H.; Harroun, T.A.; Katsaras, J.; Wassall, S.R. Cholesterol Shows Preference for the Interior of Polyunsaturated Lipid Membranes. J. Am. Chem. Soc. 2008, 130, 10–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  50. Melo, M.N.; Ingólfsson, H.I.; Marrink, S.J. Parameters for Martini sterols and hopanoids based on a virtual-site description. J. Chem. Phys. 2015, 143, 243152. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  51. Lorent, J.H.; Levental, K.R.; Ganesan, L.; Rivera-Longsworth, G.; Sezgin, E.; Doktorova, M.; Levental, I. Plasma membranes are asymmetric in lipid unsaturation, packing and protein shape. Nat. Chem. Biol. 2020, 16, 644–652. [Google Scholar] [CrossRef]
  52. Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef]
  53. Khan, H.M.; Souza, P.C.T.; Thallmair, S.; Barnoud, J.; deVries, A.H.; Marrink, S.J.; Reuter, N. Capturing Choline–Aromatics Cation–π Interactions in the MARTINI Force Field. J. Chem. Theory Comput. 2020, 16, 2550–2560. [Google Scholar] [CrossRef]
  54. Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef] [Green Version]
  55. de Jong, D.H.; Baoukina, S.; Ingólfsson, H.I.; Marrink, S.J. Martini straight: Boosting performance using a shorter cutoff and GPUs. Comput. Phys. Commun. 2016, 199, 1–7. [Google Scholar] [CrossRef]
  56. MATLAB. Version R2019b; The MathWorks Inc.: Natick, MA, USA, 2010. [Google Scholar]
  57. Lie, H.C.; Fackeldey, K.; Weber, M. A Square Root Approximation of Transition Rates for a Markov State Model. SIAM J. Matrix Anal. Appl. 2013, 34, 738–756. [Google Scholar] [CrossRef] [Green Version]
  58. Donati, L.; Heida, M.; Keller, B.G.; Weber, M. Estimation of the infinitesimal generator by square-root approximation. J. Phys. Condens. Matter 2018, 30, 425201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  59. Donati, L. Reweighting Methods for Molecular Dynamics. 2019. Available online: http://dx.doi.org/10.17169/refubium-2305 (accessed on 31 August 2022).
  60. Qiao, B.; Jiménez-Ángeles, F.; Nguyen, T.D.; de la Cruz, M.O. Water follows polar and nonpolar protein surface domains. Proc. Natl. Acad. Sci. USA 2019, 116, 19274–19281. [Google Scholar] [CrossRef] [Green Version]
  61. Heida, M. Convergences of the square-root approximation scheme to the Fokker-Planck operator. Math. Model. Methods Appl. Sci. 2018, 28, 2599–2635. [Google Scholar] [CrossRef] [Green Version]
  62. Donati, L.; Weber, M.; Keller, B.G. Markov models from the square root approximation of the Fokker-Planck equation: Calculating the grid-dependent flux. J. Phys. Condens. Matter. 2021, 33, 115902. [Google Scholar] [CrossRef] [PubMed]
  63. Souza, P.C.T.; Alessandri, R.; Barnoud, J.; Thallmair, S.; Faustino, I.; Grünewald, F.; Patmanidis, I.; Abdizadeh, H.; Bruininks, B.M.H.; Wassenaar, T.A.; et al. Martini 3: A general purpose force field for coarse-grained molecular dynamics. Nat. Methods 2021, 18, 382–388. [Google Scholar] [CrossRef] [PubMed]
  64. Alessandri, R.; Barnoud, J.; Gertsen, A.S.; Patmanidis, I.; de Vries, A.H.; Souza, P.C.T.; Marrink, S.J. Martini 3 Coarse-Grained Force Field: Small Molecules. Adv. Theory Simul. 2022, 5, 2100391. [Google Scholar] [CrossRef]
  65. Sampaio, J.L.; Gerl, M.J.; Klose, C.; Ejsing, C.S.; Beug, H.; Simons, K.; Shevchenko, A. Membrane lipidome of an epithelial cell line. Proc. Natl. Acad. Sci. USA 2011, 108, 1903–1907. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  66. Faulkner, C.; Santos-Carballal, D.; Plant, D.F.; de Leeuw, N.H. Atomistic Molecular Dynamics Simulations of Propofol and Fentanyl in Phosphatidylcholine Lipid Bilayers. ACS Omega 2020, 5, 14340–14353. [Google Scholar] [CrossRef]
  67. Yuan, X.; Raniolo, S.; Limongelli, V.; Xu, Y. The Molecular Mechanism Underlying Ligand Binding to the Membrane-Embedded Site of a G-Protein-Coupled Receptor. J. Chem. Theory Comput. 2018, 14, 2761–2770. [Google Scholar] [CrossRef] [PubMed]
  68. Lüllmann, H.; Martins, B.S.; Peters, T. pH-dependent accumulation of fentanyl, lofentanil and alfentanil by beating guineapig atria. BJA Br. J. Anaesth. 1985, 57, 1012–1017. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  69. Bower, S. Plasma protein binding of fentanyl. J. Pharm. Pharmacol. 1981, 33, 507–514. [Google Scholar] [CrossRef] [PubMed]
  70. Del Vecchio, G.; Labuz, D.; Temp, J.; Seitz, V.; Kloner, M.; Negrete, R.; Rodriguez-Gaztelumendi, A.; Weber, M.; Machelska, H.; Stein, C. pKa of opioid ligands as a discriminating factor for side effects. Sci. Rep. 2019, 9, 19344. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  71. Rosas, R.; Huang, X.P.; Roth, B.L.; Dockendorff, C. β-Fluorofentanyls Are pH-Sensitive Mu Opioid Receptor Agonists. ACS Med. Chem. Lett. 2019, 10, 1353–1356. [Google Scholar] [CrossRef] [PubMed]
Biophysica 03 00017 g001 550
Figure 1. FA to CG ligand mapping and CG system setup. (a,b) The FA ligands were transformed into CG ligands using MARTINI 2.0 mapping scheme [12], as depicted for the deprotonated NFEPP. The B4 CG bead is Q0 for protonated fentanyl and protonated NFEPP molecules. The B5 CG bead is C2 for protonated fentanyl molecules. Other CG beads in protonated fentanyl and protonated NFEPP molecules are the same as those for deprotonated NFEPP molecules. (c) Initial CG simulation setup of a membrane-embedded MOR at pH 7.4, surrounded by solvent and four deprotonated NFEPP molecules shown in black, red, grey and violet.
Figure 1. FA to CG ligand mapping and CG system setup. (a,b) The FA ligands were transformed into CG ligands using MARTINI 2.0 mapping scheme [12], as depicted for the deprotonated NFEPP. The B4 CG bead is Q0 for protonated fentanyl and protonated NFEPP molecules. The B5 CG bead is C2 for protonated fentanyl molecules. Other CG beads in protonated fentanyl and protonated NFEPP molecules are the same as those for deprotonated NFEPP molecules. (c) Initial CG simulation setup of a membrane-embedded MOR at pH 7.4, surrounded by solvent and four deprotonated NFEPP molecules shown in black, red, grey and violet.
Biophysica 03 00017 g001
Biophysica 03 00017 g002 550
Figure 2. Effect of additional DSB on the distance between TM6 and TM7. Trajectory snapshot at 500 ns of the respective simulations, depicting FA representation of TM6 and TM7 helices of the MOR, (a) without and (b) with an additional CYS 2926.47− CYS 3217.38 DSB. The variation of the TM6–TM7 distances in (c) FA and (d) CG simulation trajectories as a function of system acidity, and with and without an additional DSB.
Figure 2. Effect of additional DSB on the distance between TM6 and TM7. Trajectory snapshot at 500 ns of the respective simulations, depicting FA representation of TM6 and TM7 helices of the MOR, (a) without and (b) with an additional CYS 2926.47− CYS 3217.38 DSB. The variation of the TM6–TM7 distances in (c) FA and (d) CG simulation trajectories as a function of system acidity, and with and without an additional DSB.
Biophysica 03 00017 g002
Biophysica 03 00017 g003 550
Figure 3. Ligands distribution. (a,b) show the coordinates of the centres of mass of the opioid molecules; the crosses represent snapshots of the simulation trajectory. The XY plane is constructed to be perpendicular to the central axis of the MOR protein (which leads to a hole in the centre of the figure because the ligands did not enter the inside of the MOR). (c) shows the histogram of the positions of the opioid ligands along the trajectory with regard to the Z direction. This direction is parallel to the central axis of the MOR protein. Smaller values indicate a deeper propagation of the opioids into the cell membrane, which is located between −2 nm and 2 nm.
Figure 3. Ligands distribution. (a,b) show the coordinates of the centres of mass of the opioid molecules; the crosses represent snapshots of the simulation trajectory. The XY plane is constructed to be perpendicular to the central axis of the MOR protein (which leads to a hole in the centre of the figure because the ligands did not enter the inside of the MOR). (c) shows the histogram of the positions of the opioid ligands along the trajectory with regard to the Z direction. This direction is parallel to the central axis of the MOR protein. Smaller values indicate a deeper propagation of the opioids into the cell membrane, which is located between −2 nm and 2 nm.
Biophysica 03 00017 g003
Biophysica 03 00017 g004 550
Figure 4. NFEPP-MOR interaction. (a) The interaction between the NFEPP molecules and the MOR at pH 7 was analysed by calculating a variety of distances between the two sets. (a) The distances across the XY plane between the NFEPP molecules and the MOR during the simulation. (b) The Z-axis coordinate values of the centre of mass of the MOR subtracted from the corresponding values of the NFEPP molecules. (c) The minimum interatomic distances between the NFEPP molecules and MOR over the simulation period.
Figure 4. NFEPP-MOR interaction. (a) The interaction between the NFEPP molecules and the MOR at pH 7 was analysed by calculating a variety of distances between the two sets. (a) The distances across the XY plane between the NFEPP molecules and the MOR during the simulation. (b) The Z-axis coordinate values of the centre of mass of the MOR subtracted from the corresponding values of the NFEPP molecules. (c) The minimum interatomic distances between the NFEPP molecules and MOR over the simulation period.
Biophysica 03 00017 g004
Biophysica 03 00017 g005 550
Figure 5. NFEPP interaction with MOR surface. (a) Trajectory snapshot at 4.9 μ s depicting the interaction of NFEPP molecules at pH 7.4 with the membrane-bound MOR. (b) The same snapshot, tilted around 10 ∘ to the left for better visualisation, displayed with surface representation of the MOR along with the NFEPP molecules. (c) The radial distribution functions calculated to track the interaction between Ligand 1 and the MOR residues categorised into four categories across the last 250 ns of the MD simulation. (d) The minimum interatomic distances between Ligand 1 and the PHE 1563.41 residue of MOR over the simulation period, with a trajectory snapshot at 4.8 μ s as an inset figure, representing Ligand 1 and PHE 1563.41 residue in black and brown, respectively.
Figure 5. NFEPP interaction with MOR surface. (a) Trajectory snapshot at 4.9 μ s depicting the interaction of NFEPP molecules at pH 7.4 with the membrane-bound MOR. (b) The same snapshot, tilted around 10 ∘ to the left for better visualisation, displayed with surface representation of the MOR along with the NFEPP molecules. (c) The radial distribution functions calculated to track the interaction between Ligand 1 and the MOR residues categorised into four categories across the last 250 ns of the MD simulation. (d) The minimum interatomic distances between Ligand 1 and the PHE 1563.41 residue of MOR over the simulation period, with a trajectory snapshot at 4.8 μ s as an inset figure, representing Ligand 1 and PHE 1563.41 residue in black and brown, respectively.
Biophysica 03 00017 g005
Biophysica 03 00017 g006 550
Figure 6. χ -functions and eigenvalues. Using the XY-distributions shown in Figure 3a,b, we applied the SqrA method to compute the time-determining slowest processes of the systems. This information is presented as membership functions χ in (a–d). (e) shows the membership function χ in the case of an equal distribution (such as a blind probe). (f) shows the second-highest eigenvalues of the SqrA-matrices.
Figure 6. χ -functions and eigenvalues. Using the XY-distributions shown in Figure 3a,b, we applied the SqrA method to compute the time-determining slowest processes of the systems. This information is presented as membership functions χ in (a–d). (e) shows the membership function χ in the case of an equal distribution (such as a blind probe). (f) shows the second-highest eigenvalues of the SqrA-matrices.
Biophysica 03 00017 g006
Table
Table 1. CG membrane bilayer. The lipid composition of the upper and lower leaflets of the CG membrane bilayers used in the MD simulations.
Table 1. CG membrane bilayer. The lipid composition of the upper and lower leaflets of the CG membrane bilayers used in the MD simulations.
Upper LeafletPercentAcronym
1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine20POPC
1,2-dioleoyl-sn-glycero-3-phosphocholine20DOPC
1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine5POPE
1,2-dioleoyl-sn-glycero-3-phosphoethanolamine5DOPE
N-stearoyl-D-erythro-sphingosylphosphorylcholine15DOSM
N-stearoyl-D-erythro-monosialodihexosylganglioside10DPG3
Cholesterol25Chol
Lower leafletPercentAcronym
1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine5POPC
1,2-dioleoyl-sn-glycero-3-phosphocholine5DOPC
1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine20POPE
1,2-dioleoyl-sn-glycero-3-phosphoethanolamine20DOPE
1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-L-serine8POPS
1,2-dioleoyl-sn-glycero-3-phospho-L-serine7DOPS
1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoinositol-bisphosphate10POP2
Cholesterol25Chol
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Ray, S.; Fackeldey, K.; Stein, C.; Weber, M. Coarse-Grained MD Simulations of Opioid Interactions with the μ-Opioid Receptor and the Surrounding Lipid Membrane. Biophysica 2023, 3, 263-275. https://doi.org/10.3390/biophysica3020017

AMA Style

Ray S, Fackeldey K, Stein C, Weber M. Coarse-Grained MD Simulations of Opioid Interactions with the μ-Opioid Receptor and the Surrounding Lipid Membrane. Biophysica. 2023; 3(2):263-275. https://doi.org/10.3390/biophysica3020017

Chicago/Turabian Style

Ray, Sourav, Konstantin Fackeldey, Christoph Stein, and Marcus Weber. 2023. "Coarse-Grained MD Simulations of Opioid Interactions with the μ-Opioid Receptor and the Surrounding Lipid Membrane" Biophysica 3, no. 2: 263-275. https://doi.org/10.3390/biophysica3020017

APA Style

Ray, S., Fackeldey, K., Stein, C., & Weber, M. (2023). Coarse-Grained MD Simulations of Opioid Interactions with the μ-Opioid Receptor and the Surrounding Lipid Membrane. Biophysica, 3(2), 263-275. https://doi.org/10.3390/biophysica3020017

Article Metrics

Back to TopTop