Increasing the Equilibrium Solubility of Meloxicam in Aqueous Media by Using Dimethyl Sulfoxide as a Cosolvent: Correlation, Dissolution Thermodynamics and Preferential Solvation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and Reagents
2.2. Preparation of Solvent Mixtures
2.3. Solubility Determinations
2.4. Solid Phase Analyses
2.4.1. X-ray Diffraction (XRD) Analysis
2.4.2. Fourier Transform Infrared (FTIR) Analysis
3. Results and Discussion
3.1. Experimental Mole Fraction and Molarity Solubility
3.2. Solid Phases’ Analyses
3.3. Activity Coefficients in Mixed Solvents
3.4. Solubility Modeling
3.5. Apparent Thermodynamic Functions of Dissolution
3.6. Apparent Thermodynamic Quantities of Mixing
3.7. Enthalpy–Entropy Compensation Analysis
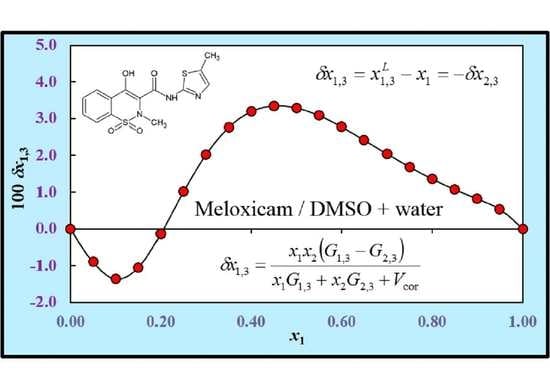
3.8. Preferential Solvation Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Budavari, S.; O’Neil, M.J.; Smith, A.; Heckelman, P.E.; Obenchain, J.R., Jr.; Gallipeau, J.A.R.; DÁrecca, M.A. The Merck Index: An Encyclopedia of Chemicals, Drugs, and Biologicals, 13th ed.; Merck & Co., Inc.: Whitehouse Station, NJ, USA, 2001. [Google Scholar]
- Brooks, P.M.; Day, R.O. Non steroidal anti-inflammatory drugs--differences and similarities. N. Engl. J. Med. 1991, 324, 1716–1725. [Google Scholar] [CrossRef] [PubMed]
- Engelhardt, G.; Homma, D.; Schlegel, K.; Utzmann, R.; Schnitzler, C. Anti-inflammatory, analgesic, antipyretic and related properties of meloxicam, a new non-steroidal anti-inflammatory agent with favourable gastrointestinal tolerance. Inflamm. Res. 1995, 44, 423–433. [Google Scholar] [CrossRef]
- Türck, D.; Roth, W.; Busch, U. A review of the clinical pharmacokinetics of meloxicam. British J. Rheumatol. 1996, 35, 13–16. [Google Scholar] [CrossRef] [PubMed]
- Sweetman, S.C. Martindale: The Complete Drug Reference, 36th ed.; Pharmaceutical Press: London, UK, 2009. [Google Scholar]
- Tinjacá, D.A.; Martínez, F.; Almanza, O.A.; Jouyban, A.; Acree, W.E., Jr. Solubility of meloxicam in aqueous binary mixtures of formamide, N-methylformamide and N,N-dimethylformamide: Determination, correlation, thermodynamics and preferential solvation. J. Chem. Thermodyn. 2021, 154, 106332. [Google Scholar] [CrossRef]
- Tinjacá, D.A.; Martínez, F.; Almanza, O.A.; Jouyban, A.; Acree, W.E., Jr. Dissolution thermodynamics and preferential solvation of meloxicam in (acetonitrile + water) mixtures. Phys. Chem. Liq. 2021, 59, 733–752. [Google Scholar] [CrossRef]
- Tinjacá, D.A.; Martínez, F.; Almanza, O.A.; Jouyban, A.; Acree, W.E., Jr. Solubility, dissolution thermodynamics and preferential solvation of meloxicam in (methanol + water) mixtures. J. Solution Chem. 2021, 50, 667–689. [Google Scholar] [CrossRef]
- Tinjacá, D.A.; Martínez, F.; Almanza, O.A.; Jouyban, A.; Acree, W.E., Jr. Solubility of meloxicam in (Carbitol® + water) mixtures: Determination, correlation, dissolution thermodynamics and preferential solvation. J. Mol. Liq. 2021, 324, 114671. [Google Scholar] [CrossRef]
- Golgoun, S.; Mokhtarpour, M.; Shekaari, H. Solubility enhancement of betamethasone, meloxicam and piroxicam by use of choline-based deep eutectic solvents. Pharm. Sci. 2021, 27, 86–101. [Google Scholar] [CrossRef]
- Tinjacá, D.A.; Martínez, F.; Almanza, O.A.; Jouyban, A.; Acree, W.E., Jr. Solubility, correlation, dissolution thermodynamics and preferential solvation of meloxicam in aqueous mixtures of 2-propanol. Pharm. Sci. 2022, 28, 130–144. [Google Scholar] [CrossRef]
- Rowe, R.C.; Sheskey, P.J.; Quinn, M.E. Handbook of Pharmaceutical Excipients, 6th ed.; American Pharmacists Association and Pharmaceutical Press: London, UK, 2009. [Google Scholar]
- Shirley, S.W.; Stewart, B.H.; Mirelman, S. Dimethyl sulfoxide in treatment of inflammatory genitourinary disorders. Urology 1978, 11, 215–220. [Google Scholar] [CrossRef]
- Jacob, S.W.; De la Torre, J.C. Dimethyl Sulfoxide (DMSO) in Trauma and Disease; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Jacob, S.W.; Herschler, R. Introductory remarks: Dimethyl sulfoxide after twenty years. Ann. N. Y. Acad. Sci. 1983, 411, 13–17. [Google Scholar] [CrossRef] [PubMed]
- Lipinski, C. Drug solubility in water and dimethylsulfoxide. In Molecular Drug Properties: Measurement and Prediction; Mannhold, R., Ed.; Wiley: Weinheim, Germany, 2007; pp. 257–282. [Google Scholar]
- Shakeel, F.; Mothana, R.A.; Haq, N.; Siddiqui, N.A.; Al-Oqail, M.M.; Al-Rehaily, A.J. Solubility and thermodynamic function of bergenin in different (DMSO + water) mixtures at different temperatures. J. Mol. Liq. 2016, 220, 823–828. [Google Scholar] [CrossRef]
- Manh, T.N.; Kim, K.-J. Solubility of N-guanylurea dinitramide in binary solvent mixtures. Propellants Explos. Pyrotech. 2016, 41, 709–712. [Google Scholar] [CrossRef]
- Jabbari, M.; Khosravi, N.; Feizabadi, M.; Ajloo, D. Solubility temperature and solvent dependence and preferential solvation of citrus flavonoid naringin in aqueous DMSO mixtures: An experimental and molecular dynamics simulation study. RSC Adv. 2017, 7, 14776–14789. [Google Scholar] [CrossRef]
- Shakeel, F.; Haq, N.; Salem-Bekhit, M.M.; Raish, M. Solubility and dissolution thermodynamics of sinapic acid in (DMSO + water) binary solvent mixtures at different temperatures. J. Mol. Liq. 2017, 225, 833–839. [Google Scholar] [CrossRef]
- Yuan, Y.; Farajtabar, A.; Kong, L.; Zhao, H. Thermodynamic solubility modelling, solvent effect and preferential solvation of p-nitrobenzamide in aqueous co-solvent mixtures of dimethyl sulfoxide, ethanol, isopropanol and ethylene glycol. J. Chem. Thermodyn. 2019, 136, 123–131. [Google Scholar] [CrossRef]
- Li, W.; Farajtabar, A.; Xing, R.; Zhu, Y.; Zhao, H. Solubility of d-histidine in aqueous cosolvent mixtures of N,N-dimethylformamide, ethanol, dimethyl sulfoxide, and N-methyl-2-pyrrolidone: Determination, preferential solvation, and solvent effect. J. Chem. Eng. Data 2020, 65, 1695–1704. [Google Scholar] [CrossRef]
- Li, X.; Zhu, Y.; Zhang, X.; Farajtabar, A.; Zhao, H. Solubility, preferential solvation, and solvent effect of micoflavin in aqueous mixtures of dimethylsulfoxide, isopropanol, propylene glycol, and ethanol. J. Chem. Eng. Data 2020, 65, 1976–1985. [Google Scholar] [CrossRef]
- Zhao, X.; Farajtabar, A.; Han, G.; Zhao, H. Phenformin in aqueous co-solvent mixtures of N,N-dimethylformamide, ethanol, N-methylpyrrolidone and dimethyl sulfoxide: Solubility, solvent effect and preferential solvation. J. Chem. Thermodyn. 2020, 144, 106085. [Google Scholar] [CrossRef]
- Alshahrani, S.M.; Shakeel, F. Solubility data and computational modeling of baricitinib in various (DMSO +Water) mixtures. Molecules 2020, 25, 2124. [Google Scholar] [CrossRef] [PubMed]
- Shakeel, F.; Alshehri, S.; Imran, M.; Haq, N.; Alanazi, A.; Anwer, M.K. Experimental and computational approaches for solubility measurement of pyridazinone derivative in binary (DMSO +water) systems. Molecules 2020, 25, 171. [Google Scholar] [CrossRef] [PubMed]
- Cysewski, P.; Przybyłek, M.; Kowalska, A.; Tymorek, N. Thermodynamics and intermolecular interactions of nicotinamide in neat and binary solutions: Experimental measurements and COSMO-RS concentration dependent reactions investigations. Int. J. Mol. Sci. 2021, 22, 7365. [Google Scholar] [CrossRef] [PubMed]
- Rubino, J.T. Cosolvents and cosolvency. In Encyclopedia of Pharmaceutical Technology; Swarbrick, J., Boylan, J.C., Eds.; Marcel Dekker, Inc.: New York, NY, USA, 1988; Volume 3, pp. 375–398. [Google Scholar]
- Martin, A.; Bustamante, P.; Chun, A.H.C. Physical Pharmacy: Physical Chemical Principles in the Pharmaceutical Sciences, 4th ed.; Lea & Febiger: Philadelphia, PA, USA, 1993. [Google Scholar]
- Yalkowsky, S.H. Solubility and Solubilization in Aqueous Media; American Chemical Society and Oxford University Press: New York, NY, USA, 1999. [Google Scholar]
- Jouyban, A. Handbook of Solubility Data for Pharmaceutical; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Delgado, D.R.; Holguin, A.R.; Almanza, O.A.; Martinez, F.; Marcus, Y. Solubility and preferential solvation of meloxicam in ethanol + water mixtures. Fluid Phase Equilib. 2011, 305, 88–95. [Google Scholar] [CrossRef]
- Higuchi, T.; Connors, K.A. Phase solubility techniques. Adv. Anal. Chem. Instrum. 1965, 4, 117–212. [Google Scholar]
- Kratky, O.; Leopold, H.; Stabinger, H. DMA45 Calculating Digital Density Meter, Instruction Manual; Anton Paar, K.G.: Graz, Austria, 1980. [Google Scholar]
- Sathesh-Babu, P.R.; Subrahmanyam, C.V.S.; Thimmasetty, J.; Manavalan, R.; Valliappan, K. Extended Hansen’s solubility approach: Meloxicam in individual solvents. Pak. J. Pharm. Sci. 2007, 20, 311–316. [Google Scholar]
- Castro, G.T.; Filippa, M.A.; Sancho, M.I.; Gasull, E.I.; Almandoz, M.C. Solvent effect on the solubility and absorption spectra of meloxicam: Experimental and theoretical calculations. Phys. Chem. Liq. 2020, 58, 337–348. [Google Scholar] [CrossRef]
- Barton, A.F.M. Handbook of Solubility Parameters and Other Cohesion Parameters, 2nd ed.; CRC Press: Boca Raton, FL, USA, 1991. [Google Scholar]
- Marcus, Y. The Properties of Solvents; John Wiley & Sons: Chichester, UK, 1998. [Google Scholar]
- Connors, K.A. Thermodynamics of Pharmaceutical Systems: An Introduction for Students of Pharmacy; Wiley–Interscience: Hoboken, NJ, USA, 2002. [Google Scholar]
- Fedors, R.F. A method for estimating both the solubility parameters and molar volumes of liquids. Polym. Eng. Sci. 1974, 14, 147–154. [Google Scholar] [CrossRef]
- Kirchner, B.; Reiher, M. The secret of dimethyl sulfoxide−water mixtures. A quantum chemical study of 1DMSO−n-water clusters. J. Am. Chem. Soc. 2002, 124, 6206–6215. [Google Scholar] [CrossRef] [PubMed]
- Lu, Z.; Manias, E.; Macdonald, D.D.; Lanagan, M. Dielectric relaxation in dimethyl sulfoxide/water mixtures studied by microwave dielectric relaxation spectroscopy. J. Phys. Chem. A 2009, 113, 12207–12214. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.Q.; Tang, P.X.; Li, S.S.; Zhang, L.L.; Li, H. X-ray powder diffraction data for meloxicam, C14H13N3O4S2. Powder Diffr. 2014, 29, 196–198. [Google Scholar] [CrossRef]
- Freitas, J.T.J.; Santos-Viana, O.M.M.; Bonfilio, R.; Doriguetto, A.C.; Benjamim de Araújo, M. Analysis of polymorphic contamination in meloxicam raw materials and its effects on the physicochemical quality of drug product. Eur. J. Pharm. Sci. 2017, 109, 347–358. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, R.; Sarkar, M. Spectroscopic studies of microenvironment dictated structural forms of piroxicam and meloxicam. J. Lumin. 2002, 99, 255–263. [Google Scholar] [CrossRef]
- Luger, P.; Daneck, K.; Engel, W.; Trummlitz, G.; Wagner, K. Structure and physicochemical properties of meloxicam, a new NSAID. Eur. J. Pharm. Sci. 1996, 4, 175–187. [Google Scholar] [CrossRef]
- Noolkar, S.B.; Jadhav, N.R.; Bhende, S.A.; Killedar, S.G. Solid-state characterization and dissolution properties of meloxicam–moringa coagulant–PVP ternary solid dispersions. AAPS PharmSciTech 2013, 14, 569–577. [Google Scholar] [CrossRef] [PubMed]
- Sirisolla, J. Solubility enhancement of meloxicam by liquisolid technique and its characterization. Int. J. Pharm. Sci. Res. 2015, 6, 835–840. [Google Scholar] [CrossRef]
- Alnaief, M.; Obaidat, R.; Mashaqbeh, H. Loading and evaluation of meloxicam and atorvastatin in carrageenan microspherical aerogels particles. J. Appl. Pharm. Sci. 2019, 9, 83–88. [Google Scholar] [CrossRef]
- Kristl, A.; Vesnaver, G. Thermodynamic investigation of the effect of octanol–water mutual miscibility on the partitioning and solubility of some guanine derivatives. J. Chem. Soc. Faraday Trans. 1995, 91, 995–998. [Google Scholar] [CrossRef]
- Jouyban, A.; Acree, W.E., Jr. Mathematical derivation of the Jouyban-Acree model to represent solute solubility data in mixed solvents at various temperatures. J. Mol. Liq. 2018, 256, 541–547. [Google Scholar] [CrossRef]
- Jouyban-Gharamaleki, A.; Valaee, L.; Barzegar-Jalali, M.; Clark, B.J.; Acree, W.E., Jr. Comparison of various cosolvency models for calculating solute solubility in water-cosolvent mixtures. Int. J. Pharm. 1999, 177, 93–101. [Google Scholar] [CrossRef]
- Yalkowsky, S.H.; Roseman, T.J. Solubilization of drugs by cosolvents. In Techniques of Solubilization of Drugs; Yalkowsky, S.H., Ed.; Marcel Dekker: New York, NY, USA, 1981; pp. 91–134. [Google Scholar]
- Jouyban, A.; Romero, S.; Chan, H.K.; Clark, B.J.; Bustamante, P. A cosolvency model to predict solubility of drugs at several temperatures from a limited number of solubility measurements. Chem. Pharm. Bull. 2002, 50, 594–599. [Google Scholar] [CrossRef] [PubMed]
- Dadmand, S.; Kamari, F.; Acree, W.E., Jr.; Jouyban, A. Solubility prediction of drugs in binary solvent mixtures at various temperatures using a minimum number of experimental data points. AAPS PharmSciTech 2019, 20, 10. [Google Scholar] [CrossRef]
- Rahimpour, E.; Jouyban, A. Utilizing Abraham and Hansen solvation parameters for solubility prediction of meloxicam in cosolvency systems. J. Mol. Liq. 2021, 328, 115400. [Google Scholar] [CrossRef]
- Krug, R.R.; Hunter, W.G.; Grieger, R.A. Enthalpy-entropy compensation. 1. Some fundamental statistical problems associated with the analysis of van’t Hoff and Arrhenius data. J. Phys. Chem. 1976, 80, 2335–2341. [Google Scholar] [CrossRef]
- Krug, R.R.; Hunter, W.G.; Grieger, R.A. Enthalpy-entropy compensation. 2. Separation of the chemical from the statistical effect. J. Phys. Chem. 1976, 80, 2341–2351. [Google Scholar] [CrossRef]
- Ruidiaz, M.A.; Delgado, D.R.; Martínez, F.; Marcus, Y. Solubility and preferential solvation of indomethacin in 1,4-dioxane + water solvent mixtures. Fluid Phase Equilib. 2010, 299, 259–265. [Google Scholar] [CrossRef]
- Aydi, A.; Dali, I.; Ghachem, K.; Al-Khazaal, A.Z.; Delgado, D.R.; Kolsi, L. Solubility of Hydroxytyrosol in binary mixture of ethanol + water from (293.15 to 318.15) K: Measurement, correlation, dissolution thermodynamics and preferential solvation. Alex. Eng. J. 2021, 60, 905–914. [Google Scholar] [CrossRef]
- Bevington, P.R. Data Reduction and Error Analysis for the Physical Sciences; McGraw-Hill Book, Co.: New York, NY, USA, 1969; pp. 56–65. [Google Scholar]
- Carstensen, J.T. Modeling and Data Treatment in the Pharmaceutical Sciences; Technomic Publishing Co., Inc.: Lancaster, PA, USA, 1996; pp. 127–159. [Google Scholar]
- Barrante, J.R. Applied Mathematics for Physical Chemistry, 2nd ed.; Prentice Hall, Inc.: Upper Saddle River, NJ, USA, 1998; 227p. [Google Scholar]
- Perlovich, G.L.; Kurkov, S.V.; Kinchin, A.N.; Bauer-Brandl, A. Thermodynamics of solutions III: Comparison of the solvation of (+)-naproxen with other NSAIDs. Eur. J. Pharm. Biopharm. 2004, 57, 411–420. [Google Scholar] [CrossRef] [PubMed]
- Delgado, D.R.; Almanza, O.A.; Martínez, F.; Peña, M.A.; Jouyban, A.; Acree, W.E., Jr. Solution thermodynamics and preferential solvation of sulfamethazine in (methanol + water) mixtures. J. Chem. Thermodyn. 2016, 97, 264–276. [Google Scholar] [CrossRef]
- Jouyban, K.; Agha, E.M.H.; Hemmati, S.; Martinez, F.; Kuentz, M.; Jouyban, A. Solubility of 5-aminosalicylic acid in N-methyl-2-pyrrolidone + water mixtures at various temperatures. J. Mol. Liq. 2020, 310, 113143. [Google Scholar] [CrossRef]
- Romero, S.; Reillo, A.; Escalera, B.; Bustamante, P. The behaviour of paracetamol in mixtures of aprotic and amphiprotic-aprotic solvents. Relationship of solubility curves to specific and nonspecific interactions. Chem. Pharm. Bull. 1996, 44, 1061–1066. [Google Scholar] [CrossRef]
- Tomlinson, E. Enthalpy-entropy compensation analysis of pharmaceutical, biochemical and biological systems. Int. J. Pharm. 1983, 13, 115–144. [Google Scholar] [CrossRef]
- Leffler, J.E.; Grunwald, E. Rates and Equilibria of Organic Reactions: As Treated by Statistical, Thermodynamic and Extrathermodynamic Methods; Dover Publications Inc.: New York, NY, USA, 1989. [Google Scholar]
- Bustamante, P.; Romero, S.; Reillo, A. Thermodynamics of paracetamol in amphiprotic and amphiprotic-aprotic solvent mixtures. Pharm. Pharmacol. Commun. 1995, 1, 505–507. [Google Scholar] [CrossRef]
- Bustamante, P.; Romero, S.; Peña, A.; Escalera, B.; Reillo, A. Nonlinear enthalpy-entropy compensation for the solubility of drugs in solvent mixtures: Paracetamol, acetanilide and nalidixic acid in dioxane-water. J. Pharm. Sci. 1998, 87, 1590–1596. [Google Scholar] [CrossRef] [PubMed]
- Martínez, F.; Peña, M.A.; Bustamante, P. Thermodynamic analysis and enthalpy-entropy compensation for the solubility of indomethacin in aqueous and non-aqueous mixtures. Fluid Phase Equilib. 2011, 308, 98–106. [Google Scholar] [CrossRef]
- Marcus, Y. Solvent Mixtures: Properties and Selective Solvation; Marcel Dekker, Inc.: New York, NY, USA, 2002. [Google Scholar]
- Marcus, Y. On the preferential solvation of drugs and PAHs in binary solvent mixtures. J. Mol. Liq. 2008, 140, 61–67. [Google Scholar] [CrossRef]
- Marcus, Y. Preferential solvation of drugs in binary solvent mixtures. Pharm. Anal. Acta 2017, 8, 1000537. [Google Scholar] [CrossRef]
- Martínez, F.; Jouyban, A.; Acree, W.E., Jr. Modelling the solubility and preferential solvation of bergenin in DMSO + water mixtures. Lat. Am. J. Pharm. 2016, 35, 2185–2190. [Google Scholar]
- Ben–Naim, A. Preferential solvation in two- and in three-component systems. Pure Appl. Chem. 1990, 62, 25–34. [Google Scholar] [CrossRef]
- Marcus, Y. Solubility and solvation in mixed solvent systems. Pure Appl. Chem. 1990, 62, 2069–2076. [Google Scholar] [CrossRef]
- Acree, W.E., Jr. IUPAC-NIST Solubility Data Series. 102. Solubility of nonsteroidal anti-inflammatory drugs (NSAIDs) in neat organic solvents and organic solvent mixtures. J. Phys. Chem. Ref. Data 2014, 43, 023102. [Google Scholar] [CrossRef]








| x1 a,b | T/K b | ||||
|---|---|---|---|---|---|
| 293.15 | 298.15 | 303.15 | 308.15 | 313.15 | |
| 0.000 c | 1.088 × 10−6 | 1.137 × 10−6 | 1.187 × 10−6 | 1.262 × 10−6 | 1.329 × 10−6 |
| 0.100 | 3.394 × 10−6 | 3.497 × 10−6 | 3.656 × 10−6 | 3.800 × 10−6 | 3.909 × 10−6 |
| 0.200 | 7.879 × 10−6 | 8.835 × 10−6 | 9.860 × 10−6 | 1.067 × 10−5 | 1.182 × 10−5 |
| 0.300 | 2.303 × 10−5 | 2.705 × 10−5 | 3.104 × 10−5 | 3.777 × 10−5 | 4.406 × 10−5 |
| 0.400 | 9.685 × 10−5 | 1.124 × 10−4 | 1.355 × 10−4 | 1.567 × 10−4 | 1.892 × 10−4 |
| 0.500 | 3.461 × 10−4 | 3.972 × 10−4 | 4.788 × 10−4 | 5.510 × 10−4 | 6.719 × 10−4 |
| 0.600 | 7.750 × 10−4 | 9.861 × 10−4 | 1.303 × 10−3 | 1.643 × 10−3 | 2.012 × 10−3 |
| 0.700 | 1.509 × 10−3 | 1.878 × 10−3 | 2.260 × 10−3 | 2.885 × 10−3 | 3.655 × 10−3 |
| 0.800 | 2.739 × 10−3 | 3.339 × 10−3 | 3.954 × 10−3 | 4.996 × 10−3 | 6.230 × 10−3 |
| 0.900 | 4.337 × 10−3 | 5.298 × 10−3 | 6.245 × 10−3 | 7.742 × 10−3 | 9.553 × 10−3 |
| 1.000 | 6.624 × 10−3 | 7.909 × 10−3 | 9.187 × 10−3 | 1.135 × 10−2 | 1.381 × 10−2 |
| Ideal c | 2.607 × 10−3 | 3.079 × 10−3 | 3.627 × 10−3 | 4.260 × 10−3 | 4.991 × 10−3 |
| x1 a,b | T/K b | ||||
|---|---|---|---|---|---|
| 293.15 | 298.15 | 303.15 | 308.15 | 313.15 | |
| 0.000 c | 6.025 × 10−5 | 6.290 × 10−5 | 6.557 × 10−5 | 6.962 × 10−5 | 7.319 × 10−5 |
| 0.100 | 1.475 × 10−4 | 1.516 × 10−4 | 1.582 × 10−4 | 1.640 × 10−4 | 1.683 × 10−4 |
| 0.200 | 2.818 × 10−4 | 3.150 × 10−4 | 3.506 × 10−4 | 3.780 × 10−4 | 4.176 × 10−4 |
| 0.300 | 6.963 × 10−4 | 8.153 × 10−4 | 9.328 × 10−4 | 1.131 × 10−3 | 1.315 × 10−3 |
| 0.400 | 2.525 × 10−3 | 2.923 × 10−3 | 3.512 × 10−3 | 4.043 × 10−3 | 4.864 × 10−3 |
| 0.500 | 7.909 × 10−3 | 9.034 × 10−3 | 1.087 × 10−2 | 1.245 × 10−2 | 1.512 × 10−2 |
| 0.600 | 1.575 × 10−2 | 1.992 × 10−2 | 2.622 × 10−2 | 3.288 × 10−2 | 4.006 × 10−2 |
| 0.700 | 2.753 × 10−2 | 3.409 × 10−2 | 4.081 × 10−2 | 5.176 × 10−2 | 6.522 × 10−2 |
| 0.800 | 4.531 × 10−2 | 5.485 × 10−2 | 6.459 × 10−2 | 8.099 × 10−2 | 0.1002 |
| 0.900 | 6.552 × 10−2 | 7.942 × 10−2 | 9.297 × 10−2 | 0.1144 | 0.1398 |
| 1.000 | 9.195 × 10−2 | 0.1089 | 0.1255 | 0.1536 | 0.1851 |
| Peak | 2θ | d-Spacing/Å | Height/Counts | Relative Intensity (%) |
|---|---|---|---|---|
| 1 | 12.98 | 6.81 | 3752.7 | 34.0 |
| 2 | 13.41 | 6.60 | 1909.4 | 17.3 |
| 3 | 14.89 | 5.95 | 6361.9 | 57.7 |
| 4 | 17.80 | 4.98 | 1376.8 | 12.5 |
| 5 | 18.57 | 4.77 | 4630.4 | 42.0 |
| 6 | 19.20 | 4.62 | 2633.3 | 23.9 |
| 7 | 20.39 | 4.35 | 1483.6 | 13.5 |
| 8 | 21.93 | 4.05 | 1346.4 | 12.2 |
| 9 | 23.11 | 3.85 | 1185.2 | 10.8 |
| 10 | 25.40 | 3.50 | 1325.3 | 12.0 |
| 11 | 25.79 | 3.45 | 11,029.5 | 100.0 |
| 12 | 26.27 | 3.39 | 2203.8 | 20.0 |
| 13 | 29.47 | 3.03 | 1585.0 | 14.4 |
| 14 | 39.75 | 2.27 | 1853.3 | 16.8 |
| x1 a,b | T/K b | ||||
|---|---|---|---|---|---|
| 293.15 | 298.15 | 303.15 | 308.15 | 313.15 | |
| 0.000 c | 2396 | 2708 | 3055 | 3376 | 3755 |
| 0.100 | 768 | 881 | 992 | 1121 | 1277 |
| 0.200 | 331 | 349 | 368 | 399 | 422 |
| 0.300 | 113 | 114 | 117 | 113 | 113 |
| 0.400 | 26.9 | 27.4 | 26.8 | 27.2 | 26.4 |
| 0.500 | 7.53 | 7.75 | 7.57 | 7.73 | 7.43 |
| 0.600 | 3.36 | 3.12 | 2.78 | 2.59 | 2.48 |
| 0.700 | 1.73 | 1.64 | 1.60 | 1.48 | 1.37 |
| 0.800 | 0.952 | 0.922 | 0.917 | 0.853 | 0.801 |
| 0.900 | 0.601 | 0.581 | 0.581 | 0.550 | 0.522 |
| 1.000 | 0.394 | 0.389 | 0.395 | 0.375 | 0.361 |
| x1 a,b | ∆solnG°/ kJ·mol−1 b | ∆solnH°/ kJ·mol−1 b | ∆solnS°/ J·mol−1·K−1 b | T∆solnS°/ kJ·mol−1 b | ζHc | ζTSc |
|---|---|---|---|---|---|---|
| 0.000 d | 34.35 | 7.69 | –87.99 | −26.66 | 0.224 | 0.776 |
| 0.100 | 31.55 | 5.59 | –85.68 | −25.96 | 0.177 | 0.823 |
| 0.200 | 29.08 | 15.27 | –45.55 | −13.80 | 0.525 | 0.475 |
| 0.300 | 26.09 | 24.89 | –3.96 | −1.20 | 0.954 | 0.046 |
| 0.400 | 22.46 | 25.49 | 9.99 | 3.03 | 0.894 | 0.106 |
| 0.500 | 19.27 | 25.23 | 19.65 | 5.96 | 0.809 | 0.191 |
| 0.600 | 16.80 | 36.95 | 66.49 | 20.15 | 0.647 | 0.353 |
| 0.700 | 15.28 | 33.53 | 60.23 | 18.25 | 0.648 | 0.352 |
| 0.800 | 13.86 | 31.20 | 57.24 | 17.34 | 0.643 | 0.357 |
| 0.900 | 12.73 | 29.87 | 56.58 | 17.14 | 0.635 | 0.365 |
| 1.000 | 11.74 | 27.91 | 53.35 | 16.16 | 0.633 | 0.367 |
| Ideal d | 14.16 | 24.78 | 35.03 | 10.61 | 0.700 | 0.300 |
| x1 a,b | ∆mixG°/ kJ·mol−1 b | ∆mixH°/ kJ·mol−1 b | ∆mixS°/ J·mol−1·K−1 b | T∆mixS°/ kJ·mol−1 b | ζHc | ζTSc |
|---|---|---|---|---|---|---|
| 0.000 | 20.19 | −17.09 | −123.02 | −37.27 | 0.314 | 0.686 |
| 0.100 | 17.38 | −19.19 | −120.71 | −36.57 | 0.344 | 0.656 |
| 0.200 | 14.91 | −9.50 | −80.58 | −24.42 | 0.280 | 0.720 |
| 0.300 | 11.93 | 0.12 | −38.99 | −11.81 | 0.010 | 0.990 |
| 0.400 | 8.30 | 0.71 | −25.03 | −7.59 | 0.086 | 0.914 |
| 0.500 | 5.11 | 0.45 | −15.38 | −4.66 | 0.088 | 0.912 |
| 0.600 | 2.64 | 12.17 | 31.46 | 9.53 | 0.561 | 0.439 |
| 0.700 | 1.12 | 8.75 | 25.20 | 7.63 | 0.534 | 0.466 |
| 0.800 | −0.30 | 6.43 | 22.21 | 6.73 | 0.489 | 0.511 |
| 0.900 | −1.43 | 5.10 | 21.55 | 6.53 | 0.438 | 0.562 |
| 1.000 | −2.42 | 3.13 | 18.32 | 5.55 | 0.361 | 0.639 |
| x1 a | D/ kJ·mol−1 | G1,3/ cm3·mol−1 | G2,3/ cm3·mol−1 | Vcor/ cm3·mol−1 | 100 δx1,3 |
|---|---|---|---|---|---|
| 0.00 | −15.72 | −297.0 | −182.2 | 830 | 0.00 |
| 0.05 | −21.33 | −335.5 | −212.0 | 876 | −0.89 |
| 0.10 | −25.61 | −353.3 | −253.3 | 926 | −1.36 |
| 0.15 | −28.68 | −352.2 | −296.1 | 984 | −1.05 |
| 0.20 | −30.65 | −338.1 | −332.4 | 1047 | −0.13 |
| 0.25 | −31.65 | −317.6 | −358.6 | 1111 | 1.01 |
| 0.30 | −31.80 | −295.3 | −374.6 | 1173 | 2.03 |
| 0.35 | −31.20 | −274.2 | −381.9 | 1231 | 2.76 |
| 0.40 | −29.98 | −255.5 | −382.3 | 1286 | 3.19 |
| 0.45 | −28.26 | −239.7 | −377.7 | 1337 | 3.34 |
| 0.50 | −26.16 | −226.6 | −369.7 | 1386 | 3.29 |
| 0.55 | −23.78 | −216.1 | −359.4 | 1433 | 3.08 |
| 0.60 | −21.26 | −207.7 | −348.1 | 1478 | 2.78 |
| 0.65 | −18.70 | −201.1 | −336.5 | 1522 | 2.42 |
| 0.70 | −16.24 | −196.0 | −325.7 | 1566 | 2.05 |
| 0.75 | −13.97 | −192.1 | −316.8 | 1610 | 1.69 |
| 0.80 | −12.03 | −189.2 | −311.5 | 1654 | 1.36 |
| 0.85 | −10.54 | −187.1 | −312.5 | 1697 | 1.07 |
| 0.90 | −9.60 | −185.5 | −325.1 | 1741 | 0.82 |
| 0.95 | −9.33 | −184.1 | −362.4 | 1783 | 0.53 |
| 1.00 | −9.86 | −182.0 | −465.7 | 1823 | 0.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tinjacá, D.A.; Martínez, F.; Almanza, O.A.; Peña, M.Á.; Jouyban, A.; Acree, W.E., Jr. Increasing the Equilibrium Solubility of Meloxicam in Aqueous Media by Using Dimethyl Sulfoxide as a Cosolvent: Correlation, Dissolution Thermodynamics and Preferential Solvation. Liquids 2022, 2, 161-182. https://doi.org/10.3390/liquids2030011
Tinjacá DA, Martínez F, Almanza OA, Peña MÁ, Jouyban A, Acree WE Jr. Increasing the Equilibrium Solubility of Meloxicam in Aqueous Media by Using Dimethyl Sulfoxide as a Cosolvent: Correlation, Dissolution Thermodynamics and Preferential Solvation. Liquids. 2022; 2(3):161-182. https://doi.org/10.3390/liquids2030011
Chicago/Turabian StyleTinjacá, Darío A., Fleming Martínez, Ovidio A. Almanza, M. Ángeles Peña, Abolghasem Jouyban, and William E. Acree, Jr. 2022. "Increasing the Equilibrium Solubility of Meloxicam in Aqueous Media by Using Dimethyl Sulfoxide as a Cosolvent: Correlation, Dissolution Thermodynamics and Preferential Solvation" Liquids 2, no. 3: 161-182. https://doi.org/10.3390/liquids2030011
APA StyleTinjacá, D. A., Martínez, F., Almanza, O. A., Peña, M. Á., Jouyban, A., & Acree, W. E., Jr. (2022). Increasing the Equilibrium Solubility of Meloxicam in Aqueous Media by Using Dimethyl Sulfoxide as a Cosolvent: Correlation, Dissolution Thermodynamics and Preferential Solvation. Liquids, 2(3), 161-182. https://doi.org/10.3390/liquids2030011