Large-Sample Asymptotic Approximations for the Sampling and Posterior Distributions of Differential Entropy for Multivariate Normal Distributions
Abstract
:1. Introduction
2. General Result
2.1. Cumulant-Generating Function, Cumulants, and Central Moments of U
2.2. Asymptotic Expansion
2.3. Asymptotic Distribution of U
3. Application to Differential Entropy
3.1. Sampling Distribution
3.2. Posterior Distribution
4. Application to Mutual Information and Multiinformation
4.1. Sampling Mean
4.2. Posterior Mean
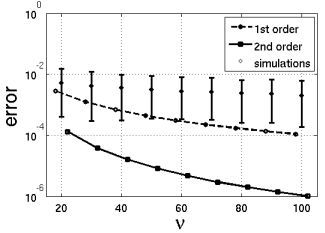
5. Simulation Study
6. Discussion

Acknowledgements
References
- Ahmed, N.A.; Gokhale, D.V. Entropy expressions and their estimators for multivariate distributions. IEEE Trans. Inform. Theory 1989, 35, 688–692. [Google Scholar] [CrossRef]
- Misra, N.; Singh, H.; Demchuk, E. Estimation of the entropy of a multivariate normal distribution. J. Multivariate Anal. 2005, 92, 324–342. [Google Scholar] [CrossRef]
- Gupta, M.; Srivastava, S. Parametric Bayesian estimation od differential entropy and relative entropy. Entropy 2010, 12, 818–843. [Google Scholar] [CrossRef]
- Beirlant, J.; Dudewicz, E.J.; Györfi, L.; van der Meulen, E.C. Nonparametric entropy estimation: An overview. Int. J. Math. Stastist. Sci. 1997, 6, 17–39. [Google Scholar]
- Strong, S.P.; Koberle, R.; de Ruyter van Steveninck, R.R.; Bialek, W. Entropy and information in neural spike trains. Phys. Rev. Lett. 1998, 80, 197–200. [Google Scholar] [CrossRef]
- Antos, A.; Kontoyiannis, I. Convergence properties of functional estimates for discrete distributions. Random Struct. Algor. 2001, 19, 163–193. [Google Scholar] [CrossRef]
- Paninski, L. Estimation of entropy and mutual information. Neural Comput. 2003, 15, 1191–1253. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Wolf, D.R. Estimating functions of probability distributions from a finite set of samples. Phys. Rev. E 1995, 52, 6841–6854. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Wolf, D.R. Erratum: Estimating functions of probability distributions from a finite set of samples. Phys. Rev. E 1996, 54, 6973. [Google Scholar] [CrossRef]
- Anderson, T.W. An Introduction to Multivariate Statistical Analysis; John Wiley and Sons: New York, NY, USA, 1958. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Applied Mathematics Series 55; National Bureau of Standards: Washington, DC, USA, 1972. [Google Scholar]
- Anderson, T.W. An Introduction to Multivariate Statistical Analysis, 3rd ed.; Series in Probability and Mathematical Statistics; John Wiley and Sons: New York, NY, USA, 2003. [Google Scholar]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Rubin, D.B. Bayesian Data Analysis; Texts in Statistical Science; Chapman & Hall: London, UK, 1998. [Google Scholar]
- Watanabe, S. Information theoretical analysis of multivariate correlation. IBM J. Res. Dev. 1960, 4, 66–82. [Google Scholar] [CrossRef]
- Garner, W.R. Uncertainty and Structure as Psychological Concepts; John Wiley & Sons: New York, NY, USA, 1962. [Google Scholar]
- Joe, H. Relative entropy measures of multivariate dependence. J. Am. Statist. Assoc. 1989, 84, 157–164. [Google Scholar] [CrossRef]
- Studený, M.; Vejnarová, J. The multiinformation function as a tool for measuring stochastic dependence. In Proceedings of the NATO Advanced Study Institute on Learning in Graphical Models; Jordan, M.I., Ed.; MIT Press: Cambridge, MA, USA, 1998; pp. 261–298. [Google Scholar]
- Press, S.J. Applied Multivariate Analysis. Using Bayesian and Frequentist Methods of Inference, 2nd ed.; Dover: Mineola, NY, USA, 2005. [Google Scholar]
- Kullback, S. Information Theory and Statistics; Dover: Mineola, NY, USA, 1968. [Google Scholar]
- Chen, C.P. Inequalities for the polygamma functions with application. Gener. Math. 2005, 13, 65–72. [Google Scholar]
Appendix
1. Results for
2. Results for ,
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Marrelec, G.; Benali, H. Large-Sample Asymptotic Approximations for the Sampling and Posterior Distributions of Differential Entropy for Multivariate Normal Distributions. Entropy 2011, 13, 805-819. https://doi.org/10.3390/e13040805
Marrelec G, Benali H. Large-Sample Asymptotic Approximations for the Sampling and Posterior Distributions of Differential Entropy for Multivariate Normal Distributions. Entropy. 2011; 13(4):805-819. https://doi.org/10.3390/e13040805
Chicago/Turabian StyleMarrelec, Guillaume, and Habib Benali. 2011. "Large-Sample Asymptotic Approximations for the Sampling and Posterior Distributions of Differential Entropy for Multivariate Normal Distributions" Entropy 13, no. 4: 805-819. https://doi.org/10.3390/e13040805
APA StyleMarrelec, G., & Benali, H. (2011). Large-Sample Asymptotic Approximations for the Sampling and Posterior Distributions of Differential Entropy for Multivariate Normal Distributions. Entropy, 13(4), 805-819. https://doi.org/10.3390/e13040805