Time Series Analysis Using Composite Multiscale Entropy
Abstract
:1. Introduction
2. Methods
2.1. Multiscale Entropy


2.2. Composite Multiscale Entropy


3. Comparative Study of MSE and CMSE
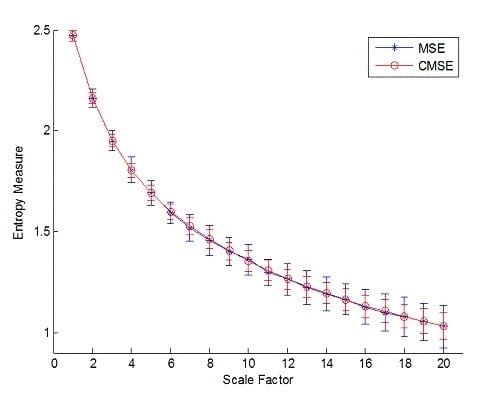
3.1. White Noise and 1/f Noise




| Data Length | Signals | Methods | Scales | ||||||||||
| 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 20 | |||
| 2,000 | white noise | MSE | 0.026 | 0.049 | 0.059 | 0.064 | 0.072 | 0.067 | 0.084 | 0.076 | 0.091 | 0.091 | 0.103 |
| CMSE | 0.026 | 0.030 | 0.037 | 0.043 | 0.046 | 0.051 | 0.054 | 0.054 | 0.057 | 0.063 | 0.066 | ||
| 1/f noise | MSE | 0.084 | 0.097 | 0.121 | 0.139 | 0.162 | 0.227 | 0.236 | 0.284 | 0.265 | 0.282 | 0.310 | |
| CMSE | 0.084 | 0.088 | 0.092 | 0.099 | 0.108 | 0.126 | 0.122 | 0.148 | 0.153 | 0.155 | 0.163 | ||
| 10,000 | white noise | MSE | 0.007 | 0.014 | 0.019 | 0.025 | 0.028 | 0.030 | 0.032 | 0.035 | 0.038 | 0.035 | 0.035 |
| CMSE | 0.007 | 0.010 | 0.015 | 0.018 | 0.020 | 0.021 | 0.023 | 0.025 | 0.025 | 0.027 | 0.028 | ||
| 1/f noise | MSE | 0.069 | 0.069 | 0.070 | 0.073 | 0.072 | 0.071 | 0.078 | 0.074 | 0.086 | 0.085 | 0.080 | |
| CMSE | 0.069 | 0.068 | 0.068 | 0.067 | 0.069 | 0.069 | 0.068 | 0.069 | 0.072 | 0.072 | 0.070 | ||
3.2. Real Vibration Data
| Shaft Speed / Defect Level | Rotation Speed (rpm) | ||||||||
| 1730 | 1750 | 1772 | |||||||
| Fault diameter (mils) | |||||||||
| Fault Class | 7 | 14 | 21 | 7 | 14 | 21 | 7 | 14 | 21 |
| Normal state | 243 | 242 | 242 | ||||||
| Ball | 244 | 243 | 243 | 243 | 243 | 243 | 243 | 243 | 243 |
| Inner race fault | 243 | 242 | 244 | 243 | 244 | 245 | 243 | 191 | 242 |
| Outer race fault (3) | 243 | 242 | 243 | 243 | 242 | 245 | |||
| Outer race fault (6) | 244 | 244 | 244 | 243 | 243 | 244 | 243 | 242 | 244 |
| Outer race fault (12) | 242 | 243 | 241 | 243 | 241 | 243 | |||


3.3. Performance Assessment
3.4. Fault Diagnosis Using an Artificial Neural Network
| Fault Class 1 | Feature Extractor | Fault class 2 | |||||
| N | B | I | O3 | O6 | O12 | ||
| N | MSE | 25.200 | 25.200 | 20.044 | 25.484 | 5.538 | |
| CMSE | 25.898 | 28.069 | 21.614 | 26.115 | 6.992 | ||
| B | MSE | 25.200 | 3.675 | 5.312 | 5.515 | 9.657 | |
| CMSE | 25.898 | 5.852 | 8.105 | 7.534 | 11.387 | ||
| I | MSE | 25.200 | 3.675 | 7.128 | 7.560 | 12.883 | |
| CMSE | 28.069 | 5.852 | 8.672 | 9.652 | 16.965 | ||
| O3 | MSE | 20.044 | 5.312 | 7.128 | 5.934 | 9.303 | |
| CMSE | 21.614 | 8.105 | 8.672 | 6.605 | 13.239 | ||
| O6 | MSE | 25.484 | 5.515 | 7.560 | 5.934 | 9.624 | |
| CMSE | 26.115 | 7.534 | 9.652 | 6.605 | 12.139 | ||
| O12 | MSE | 5.538 | 9.657 | 12.883 | 9.303 | 9.624 | |
| CMSE | 6.992 | 11.387 | 16.965 | 13.239 | 12.139 | ||
| Fault Diameter / Feature Extractor | Rotation Speed (rpm) | ||||||||
| 1730 | 1750 | 1772 | |||||||
| 7 | 14 | 21 | 7 | 14 | 21 | 7 | 14 | 21 | |
| MSE | 97.33% | 98.81% | 96.77% | 99.05% | 98.01% | 95.65% | 99.34% | 96.67% | 95.89% |
| CMSE | 99.29% | 99.75% | 98.26% | 99.58% | 99.86% | 98.50% | 99.91% | 99.65% | 98.42% |
5. Conclusions
Acknowledgments
References
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circul. Physiol. 2000, 278, H2039–H2049. [Google Scholar]
- Costa, M.; Peng, C.K.; Goldberger, A.L.; Hausdorff, J.M. Multiscale entropy analysis of human gait dynamics. Physica A 2003, 330, 53–60. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 68102. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 2005, 71, 021906. [Google Scholar] [CrossRef] [PubMed]
- Escudero, J.; Abásolo, D.; Hornero, R.; Espino, P.; López, M. Analysis of electroencephalograms in Alzheimerʼs disease patients with multiscale entropy. Physiol. Meas. 2006, 27, 1091. [Google Scholar] [CrossRef] [PubMed]
- Manor, B.; Costa, M.D.; Hu, K.; Newton, E.; Starobinets, O.; Kang, H.G.; Peng, C.; Novak, V.; Lipsitz, L.A. Physiological complexity and system adaptability: evidence from postural control dynamics of older adults. J. Appl. Physiol. 2010, 109, 1786–1791. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Xiong, G.; Liu, H.; Zou, H.; Guo, W. Bearing fault diagnosis using multi-scale entropy and adaptive neuro-fuzzy inference. Expert Syst. Appl. 2010, 37, 6077–6085. [Google Scholar] [CrossRef]
- Lin, J.L.; Liu, J.Y.C.; Li, C.W.; Tsai, L.F.; Chung, H.Y. Motor shaft misalignment detection using multiscale entropy with wavelet denoising. Expert Syst. Appl. 2010, 37, 7200–7204. [Google Scholar] [CrossRef]
- Chou, C.M. Wavelet-based multi-scale entropy analysis of complex rainfall time series. Entropy 2011, 13, 241–253. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Y.K. Multi-scale entropy analysis of Mississippi River flow. Stoch. Environ. Res. Risk Assess. 2008, 22, 507–512. [Google Scholar] [CrossRef]
- Guzmán-Vargas, L.; Ramírez-Rojas, A.; Angulo-Brown, F. Multiscale entropy analysis of electroseismic time series. Nat. Hazards Earth Syst. Sci. 2008, 8, 855–860. [Google Scholar] [CrossRef]
- Yan, R.-Y.; Zheng, Q.-H. Multi-Scale Entropy Based Traffic Analysis and Anomaly Detection. In Proceeding of Eighth International Conference on Intelligent Systems Design and Applications, ISDA 2008, Kaohsiung, Taiwan, 26–28 November, 2008; Volume 3, pp. 151–157.
- Glowinski, D.; Coletta, P.; Volpe, G.; Camurri, A.; Chiorri, C.; Schenone, A. Multi-Scale Entropy Analysis of Dominance in Social Creative Activities. In proceeding of the 18th International Conference on Multimedea, Firenze, Italy, 25–29 October, 2010; Association for Computing Machinary: New York, NY, USA, 2010; pp. 1035–1038. [Google Scholar]
- Litak, G.; Syta, A.; Rusinek, R. Dynamical changes during composite milling: recurrence and multiscale entropy analysis. Int. J. Adv. Manuf. Technol. 2011, 56, 445–453. [Google Scholar] [CrossRef]
- Borowiec, M.; Sen, A.K.; Litak, G.; Hunicz, J.; Koszałka, G.; Niewczas, A. Vibrations of a vehicle excited by real road profiles. Forsch. Ing.Wes. (Eng. Res.) 2010, 74, 99–109. [Google Scholar] [CrossRef]
- Liu, Q.; Wei, Q.; Fan, S.Z.; Lu, C.W.; Lin, T.Y.; Abbod, M.F.; Shieh, J.S. Adaptive Computation of Multiscale Entropy and Its Application in EEG Signals for Monitoring Depth of Anesthesia During Surgery. Entropy 2012, 14, 978–992. [Google Scholar] [CrossRef]
- Case Western Reserve University Bearing Data Center Website. Available online: http://csegroups.case.edu/bearingdatacenter/pages/download-data-file/ (accessed on 5 May 2011).
- Pan, Y.H.; Lin, W.Y.; Wang, Y.H.; Lee, K.T. Computing multiscale entropy with orthogonal range search. J. Mar. Sci. Technol. 2011, 19, 107–113. [Google Scholar]
- Crossman, J.A.; Guo, H.; Murphey, Y.L.; Cardillo, J. Automotive signal fault diagnostics—Part I: signal fault analysis, signal segmentation, feature extraction and quasi-optimal feature selection. IEEE Trans. Veh. Technol. 2003, 52, 1063–1075. [Google Scholar] [CrossRef]
- Hagan, M.T.; Menhaj, M.B. Training feedforward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef] [PubMed]
- Wei, Q.; Liu, D.H.; Wang, K.H.; Liu, Q.; Abbod, M.F.; Jiang, B.C.; Chen, K.P.; Wu, C.; Shieh, J.S. Multivariate multiscale entropy applied to center of pressure signals analysis: an effect of vibration stimulation of shoes. Entropy 2012, 14, 2157–2172. [Google Scholar] [CrossRef]
- Wu, S.D.; Wu, P.H.; Wu, C.W.; Ding, J.J.; Wang, C.C. Bearing fault diagnosis based on multiscale permutation entropy and support vector machine. Entropy 2012, 14, 1343–1356. [Google Scholar] [CrossRef]
- Morabito, F.C.; Labate, D.; La Foresta, F.; Bramanti, A.; Morabito, G.; Palamara, I. Multivariate multi-scale permutation entropy for complexity analysis of Alzheimer’s disease EEG. Entropy 2012, 14, 1186–1202. [Google Scholar] [CrossRef]
Appendix A. The Matlab Code for the Composite Multiscale Entropy Algorithm
function E = CMSE(data,scale)
r = 0.15*std(data);
for i = 1:scale % i:scale index
for j = 1:i % j:croasegrain series index
buf = croasegrain(data(j:end),i);
E(i) = E(i)+ SampEn(buf,r)/i;
end
end
%Coarse Grain Procedure. See Equation (2)
% iSig: input signal ; s : scale numbers ; oSig: output signal
function oSig=CoarseGrain(iSig,s)
N=length(iSig); %length of input signal
for i=1:1:N/s
oSig(i)=mean(iSig((i-1)*s+1:i*s));
end
%function to calculate sample entropy. See Algorithm 1
function entropy = SampEn(data,r)
l = length(data);
Nn = 0;
Nd = 0;
for i = 1:l-2
for j = i+1:l-2
if abs(data(i)-data(j))<r && abs(data(i+1)-data(j+1))<r
Nn = Nn+1;
if abs(data(i+2)-data(j+2))<r
Nd = Nd+1;
end
end
end
end
entropy = -log(Nd/Nn);
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wu, S.-D.; Wu, C.-W.; Lin, S.-G.; Wang, C.-C.; Lee, K.-Y. Time Series Analysis Using Composite Multiscale Entropy. Entropy 2013, 15, 1069-1084. https://doi.org/10.3390/e15031069
Wu S-D, Wu C-W, Lin S-G, Wang C-C, Lee K-Y. Time Series Analysis Using Composite Multiscale Entropy. Entropy. 2013; 15(3):1069-1084. https://doi.org/10.3390/e15031069
Chicago/Turabian StyleWu, Shuen-De, Chiu-Wen Wu, Shiou-Gwo Lin, Chun-Chieh Wang, and Kung-Yen Lee. 2013. "Time Series Analysis Using Composite Multiscale Entropy" Entropy 15, no. 3: 1069-1084. https://doi.org/10.3390/e15031069
APA StyleWu, S. -D., Wu, C. -W., Lin, S. -G., Wang, C. -C., & Lee, K. -Y. (2013). Time Series Analysis Using Composite Multiscale Entropy. Entropy, 15(3), 1069-1084. https://doi.org/10.3390/e15031069