A Load Balancing Algorithm Based on Maximum Entropy Methods in Homogeneous Clusters

Abstract

In order to solve the problems of ill-balanced task allocation, long response time, low throughput rate and poor performance when the cluster system is assigning tasks, we introduce the concept of entropy in thermodynamics into load balancing algorithms. This paper proposes a new load balancing algorithm for homogeneous clusters based on the Maximum Entropy Method (MEM). By calculating the entropy of the system and using the maximum entropy principle to ensure that each scheduling and migration is performed following the increasing tendency of the entropy, the system can achieve the load balancing status as soon as possible, shorten the task execution time and enable high performance. The result of simulation experiments show that this algorithm is more advanced when it comes to the time and extent of the load balance of the homogeneous cluster system compared with traditional algorithms. It also provides novel thoughts of solutions for the load balancing problem of the homogeneous cluster system.

1. Introduction

Nowadays, with the rapid development of information and terminal technology, the needs of information industry are moving in the direction of high-end services and low-end terminals. Therefore, the subsequent massive data integration and computing needs have become the bottleneck of the server cluster technology at the current stage [1]. As a single server would be unable to satisfy the growing demand, cluster systems—with good scalability and high performance—turn out to be the primary choice. The homogeneous cluster is a major cluster system in which each of the computing nodes in it has the same hardware and software configuration [2]. It is significant and difficult to decide how to assign tasks reasonably. This means that the tasks should be evenly distributed, which won’t make one server over-assigned and the rest less-assigned. Consequently, the load balancing mechanisms emerged and it became a main target for resource allocation of cluster system.

The load balancing technology is applied to the distribution of the load among the resources including multi-processor, multi-computer, multi-network and multiple hard drives, to evenly distribute the load. Moreover, computing load balancing implies distributing the computing tasks among different nodes in the cluster system, to improve the computing performance of whole cluster system, which is called a high-performance cluster and is widely used in fields like scientific computation. Moreover, load balancing is one of the main indexes of resource allocation in high-performance cluster systems [3].

2. Related Studies

In recent years, there have already been numerous studies about load balancing technology. It is developing towards the direction of intelligence. More and more known load balancing information and unknown predictive information have been chosen by researchers as the judgment standard of load balancing.

Ibrahim et al. [4] did a lot of research on how to use dynamic load balancing to solve the parallel search tree problem, and proposed the Round Robin dynamic load balancing algorithm, whereby all nodes in the cluster can be equally selected in a reasonable order, which is usually from the head to the tail of the list, and then again and again. However, since this algorithm does not take the current moment load of the nodes into consideration, the judgment of the dynamic load balancing is not precise enough.

Liu et al. [5] gave a load balancing optimization algorithm with a genetic algorithm. It applied the artificial intelligence technology to solving the load balancing problem. However, this algorithm can only be used in ideal situations like the laboratory, and it is unable to meet the complex needs of practical applications.

Chau [6] studied the problem of load balancing between distant clusters, proposed an improved Dimension Exchange Method (DEM) synchronous load balancing algorithm under a hypercube structure, whose performance is better than the original DEM algorithm and it is similar to the CWA algorithm. However, this paper mainly discusses the problem of load balancing within the cluster, so the algorithm isn’t applicable.

Balasubramaniam et al. [7] presented a dynamic load balancing library in clusters, which combined the technology of dynamic load balancing with round-robin scheduling, and could be used as a load balancing application interface of a distributed shared memory (DSM) system. However, the dynamic load balancing library is built on heterogeneous clusters, so it can not always be efficient on homogeneous clusters.

Sit et al. [8] studied the reasonable migration quantity of load during the migration process, proposing a dynamic load balancing algorithm based on clusters. Moreover, this algorithm mapped the load difference between the nodes to an appropriate cluster. Using the center of mass of the cluster to obtain the appropriate number of tasks that need to be migrated, it can adjust the load imbalance between the nodes. However, this algorithm only studied one aspect of a dynamic load balancing-migrate execution, while the other two aspects—information collection and migration strategy—have not been studied.

Dai et al. [9] applied the idea of fuzzy control and heuristic strategy from the traditional control theory to the load balancing problem, and presented a fuzzy control-based heuristic algorithm for load balancing in workflow engines, which offers a new idea for solving the problem of load balance.

Kim and Kim [10] presented a load balancing algorithm named Perpendicular Image Partitioning (PIP) for parallel vision processing. The algorithm is developed for a specific enviroment such as a small-scale parallel system, and it takes the load variance as the metric for load balancing. The load-balancing problem is converted to the position determination problem of partitioning lines, and the purpose of the algorithm is to find the balanced partitioning line position pair so to make the load variance becomes the minimum value, and thus achieve load balancing. As it is a data-oriented and static load balancing algorithm, it cannot satisfy well the demands of homogeneous clusters.

Nair et al. [11] considered different load balancing algorithms and the queue-size processes generated by these algorithms, and used the entropy rate of the induced queue-size process as a metric to understand the trade-off performance for implementation simplicity, it offers a new metric for load balancing.

Dong et al. [1] discussed the relationship between the load balancing problems of a cloud computing cluster system and the energy from the aspects of entropy and generalized complexity, and calculated the value of the energy which could make the cloud computing cluster system achieve an equilibrium state. This makes possible solving the problem of load balancing by using the change of entropy.

Zuo et al. [12] proposed a resource evaluation model based on entropy optimization and dynamic weighting. The entropy optimization filtered the resources that satisfy the QoS and system maximization by goal function and constraints of maximum entropy and the entropy increase principle, which achieved optimal scheduling and satisfied the QoS. Then the evaluation model evaluated the load of having filtered resources by dynamic weighted algorithm. However, in this paper, the entropy has only been used to filter the resources, and it only focused on evaluating the loads. There is no detailed description and implementation of the load balancing algorithm, so it is not feasible in homogeneous clusters.

Therefore, inspired by the related studies, this paper introduces the concept of entropy in thermodynamics into load balancing for homogeneous clusters, redefining the target of load balancing by using the entropy as a measure of the degree of load balancing, and then proposing a load balancing algorithm based on the Maximum Entropy Methods (MEM) in homogeneous clusters, which can be used to equally distribute the tasks in homogeneous clusters for reducing the response time and increasing the throughput. Compared with other traditional algorithms, the new algorithm is better in terms of the time and the degree of system load balancing, which indicates that the new algorithm is workable to a certain extent to balance the load in homogeneous cluster.

The paper is organized as follows: in Section 2, we introduce related research studies on load balancing; in Section 3, we describe the basic concepts of entropy, load balancing, and the principle of Maximum Entropy; in Section 4, we introduce the thermodynamic concept of entropy into the load balancing algorithm, defins the model and then perform the theoretical analyses; in Section 5, we present our Maximum Entropy Methods-based load balancing (MEMBLB) algorithm and give a brief introduction to it. Section 6 concerns some experiments on this algorithm and compares the algorithm with other algorithms. The last section is the conclusion of the paper and illustrates our future work plans.

3. Basic Concept

Before introducing the algorithm, it is necessary to understand the basic concepts of entropy and load balancing and the maximum entropy methods, so as to better comprehend the algorithm better.

3.1 Entropy

Entropy is a very important concept in physics, which is used to describe and study the widespread irreversibility of motion conversion direction in nature. In 1850, German physicist R. J. E. Clausius firstly used the thermodynamic state function-entropy (S) to quantitatively describe the dissipation character of changing in energy during the irreversible process, and quantize the second law of thermodynamics, so that the thermodynamics was greatly improved. The entropy is primarily used for representing the degree of uniformity of any kind of energy distribution in the space. The more uniform energy distributed, the greater the entropy. When the energy of a system achieves a completely uniform distribution, the entropy of the system reaches a maximum. See formula as follows:

$$\mathrm{\Delta }S=Q/T$$

(1)

where Q represents the change of system energy and ΔS represents the variation of entropy. Since then, the concept of entropy quickly spreaded to other fields, thus opening up new research fields one after another inside and outside physics. Nowadays, the concept of entropy not only infiltrated disciplines like chemistry, biology, mathematics, engineering, meteorology, geology and other traditional natural sciences, but also extended to many aspects of humanities and social science. Albert Einstein once said: “The entropy theory is the first rule of the whole science”. Eddington also believed that the entropy is the sovereign philosophy principle in the whole universe. Historically, all the theories (thermodynamics, statistical physics, information theory), which are known to be very successful, contained some understanding and definition of entropy. Although these understandings and definitions are not identical, there is a close relationship between them.

This section focuses on the concept of entropy in information theory, which regards entropy as an uncertainty degree of information states. In 1948, in order to emphasize the concept of “the amount of information”, Shannon connected information entropy with statistical mechanics entropy, and regarded the channel theorems as a special form of the second law of thermodynamics in communication theory, thus making information entropy a formal branch of information theory. The idea used by Shannon to break through the key concept of “the amount of information” is that, “Can I define a quantity, which can to some extent measure how much information is produced in this process? Or more ideally, how much is the information rate produced by this process?” Then, he put the amount of information as the central concept of information theory. With this idea, he used the statistical properties of Markov process, that is using the “entropy” to represent the characteristics of the information source, and given the formula of information entropy as follows:

$$H=-C{\displaystyle {\sum }_{i=1}^n{p}_i}\ln p_i$$

(2)

where p_i presents the probability of occurrence of the i^th event, C is a proportionality constant, and H is the H in the famous Boltzmann constant. The above formula when used to express the connection between the uncertainty and random events, can solve the problem of the quantitative description of information. As a measure of the loss of the system information, the information entropy means that the higher the degree of order of a system, the less the degree of uncertainty, the smaller the entropy, and the greater the amount of information; the more the degree of disorder of a system, the greater the degree of uncertainty, the greater the entropy, and the less the amount of information. “The average of the amount of the information has various characteristics of entropy” means the application of entropy will be beyond some fields of natural science by the information theory. Development of the theory mushroomed, and in 1984, Xie et al. [10] introduced the concept of entropy to measure the information of fuzzy sets, and it functioned perfectly, so the concept of entropy has been extended ever since.

3.2. Maximum Entropy Methods

There are some random events whose distribution function are unknown and cannot be calculated directly. We only know the average value of one or a few random variables related to the random event. Obviously, this kind of probability distribution is not unique, so how to select the “best” or the “most reasonable” one from the compatible distribution as the actual common distribution? To do this, we need a standard—that is Maximum Entropy Method—which is a big application of principle of entropy increase in thermodynamics [11].

According to the MEM, selecting such a distribution from all the compatible distributions means finding a distribution with the maximum information entropy under some constraint conditions—usually a certain average value of the given random variable. Based on MEM, we can find the distribution with the maximum entropy by using the Lagrange multiplier method.

The most common and most practical probability distribution corresponds to the maximum information entropy. When the information entropy takes the maximum value, the corresponding probability distribution must be the most possible one. Therefore, it is reasonable to make MEM a selection criterion. The MEM broadens the application range of entropy [12]. For engineering structural systems—due to the prior knowledge level—the difference of system decomposition method and the influence of various uncertainty factors, the system identification problem often has more than one solution, so the MEM is an effective solving method. According to the MEM, we should choose the one with maximum entropy among all the feasible solutions of an ill-posed problem. The maximum entropy means the man-made hypothesis is the minimum because of the data deficiency. Regarding entropy as an uncertain measurement, the solution here and now contains the least subjective elements, which makes it the most objective.

The mathematical model using the MEM to solve the probability distribution problem can be written as follows [13]:

Set sample data as: x_i, i = 1,2,…,n, x_i, i=1,2,…,n, so:

$$max(-{\displaystyle {\sum }_{i=1}^n{p}_i\ln p_i|s.t.{\displaystyle {\sum }_{i=1}^n{p}_i{x}_i^k={\displaystyle {\sum }_{i=1}^n{x}_i^k}/n,k=0,1,\mathrm{...},m}})$$

(3)

where s.t. represents constraint conditions, and the probability condition is ${\displaystyle {\sum }_{i=1}^n{p}_i}=1$ when k equals zero. While the rest of k = 1,2,…,m, the k origin moment is equal to the corresponding sample moment. Usually we can use the Lagrange Multiplier Method to solve it, or using the Optimization Method to work out its numerical solution.

3.3. Load Balancing

The load is an abstract concept to indicate how busy the system is and it refers to the subtasks, which are assigned to each server node and executed in parallel [14]. The so-called load balancing strategy means to balance the load of each server node by adopting certain policy to make the load essentially equal. It can be understood in two aspects: on the one hand, it refers to the allocation of large volumes of concurrent access and data traffic to multiple server nodes, and processing them separately to reduce the waiting time; on the other hand, it means that a single heavy load calculation task can be shared among multiple server nodes for dealing with it in parallel, and then summarizing the results back to the user, improving the treatment capacity of the system [15]. The mathematical model is defined as follows:

Definition 1. The so-called load-balancing means giving a set of load L={L₁,…,L_n}, a set of server nodes S={S₁,…,S_m} and a set of current server load SL={SL₁,…,SL_m}, to find a function f(L), in which the set of load L can be mapped to the set of server nodes S_i, making the load SL_i of each server node S_i be essentially equal, that is:

$$S{L}_1\cong S{L}_2\cong \dots \cong S{L}_m$$

(4)

where SL_iSLi represents the sum of all the loadfLi f(L_i) mapped to this server node S_iSi.

If we use τ_o τoto reflect the time needed for executing task L_o Loon the server node S_iSi, the time needed for executing all the task on the server node S_i Siis as follows:

$$t_i={\displaystyle {\sum }_{o\in f\left(L_i\right)\left(i=1,\dots ,n\right)}{\tau }_o}$$

(5)

Definition 2. If m equals to one, that means there is only one server node, and all the tasks should be executed serially on the server node, so the time needed is the sum of all the time, which can be represented as T₁ shown below:

$$T_1={\displaystyle \sum {\tau }_o\left(o=1,\dots ,n\right)}$$

(6)

Definition 3. If m is greater than one, that means there are more than one server node, and the tasks can be shared to multiple server nodes for dealing with in parallel, the time needed is represented as T_m shown below:

$$T_m=\underset{i=1,\dots ,n}{max}{t}_i$$

(7)

Thus, the target of the load balancing is to solve the mapping f(L) to get the minimum of T_m under the circumstance that $S{L}_1\cong S{L}_2\cong \cdots \cong S{L}_m$.

4. Model of the Algorithm and Its Properties

4.1. The Define of the Model

Through the description of the basic concept above, we find that the features of load-balancing in cluster systems have much in common with the relative concepts of thermodynamic systems [16], which means that the entropy can be used to show the randomness of material. The more uniform the distribution, the bigger the entropy. The purpose of load-balancing is the load-distribution uniformity, so we introduce the concept of entropy in thermodynamics into the cluster system and take advantage of the MEM to solve the load-balancing problems. For this we redefine some concepts of load balancing as follows:

Definition 4 (the concept of entropy). If a homogeneous cluster system has n compute nodes, so the load of the node i is L_i as well as the relative load factor is$p_i=L_i/{\displaystyle {\sum }_i{L}_i}\left(i=1,2,\dots ,n\right)$ at time t, then the system entropy value H(t) at time t can be expressed as below:

$$H\left(t\right)={\displaystyle {\sum }_{i=1}^n\left[p_i\ln \left(1/p_i\right)\right]}$$

(8)

The probability distribution of maximum entropy is:

$$max\left(-{\displaystyle {\sum }_{i=1}^n{p}_i\ln p_i|s.t.{\displaystyle {\sum }_{i=1}^n{p}_i=1}}\right)$$

(9)

Only under the probability conditions without other constraints, using Lagrange Multiplier Method, namely introducing the Lagrange multiplier λ into solving an unconstrained maximization objective function, which means to maximize the following function:

$$-{\displaystyle {\sum }_{i=1}^n{p}_i\ln p_i}+\left(\lambda +1\right)\left({\displaystyle {\sum }_{i=1}^n{p}_i}-1\right)\Rightarrow max$$

(10)

Obviously:

$$\frac{\partial }{\partial p_i}\left[-{\displaystyle {\sum }_{i=1}^n{p}_i\ln p_i}+\left(\lambda +1\right)\left({\displaystyle {\sum }_{i=1}^n{p}_i}-1\right)\right]=0$$

(11)

In order to achieve simple results, using (λ+1) instead of λ₀, and get the results: λ=ln p_i or p_i=e^λ, i=1,2,…,n.

According to the constraint conditions it should be as follows:

$${\displaystyle {\sum }_{i=1}^n{p}_i}=n{e}^{\lambda }=1\text{that is}{p}_i=e^{\lambda }=1/n,i=1,2,\dots ,n$$

(12)

Considering that the solution is a probability distribution, the maximum entropy value is:

$$H\left(t\right)={\displaystyle {\sum }_{i=1}^n\left[\left(1/n\right)\ln \left(n\right)\right]}=\ln \left(n\right)$$

(13)

From Section 3.3 we know that the target of the load balancing is to solve the mapping f(L) to get the minimum of T_m under the circumstance that $S{L}_1\cong S{L}_2\cong \cdots \cong S{L}_m$ Moreover, through the concept of entropy, we can know that the entropy will reach its maximum value when p₁ = p₂ =⋯= p_m =1/m, which equals to SL₁≅SL₂≅⋯≅SL_m. Therefore, the target of using MEM to redefine the load balancing can be described as follows:

Definition 5 (the target of load-balancing). The target of load balancing is always moving with the trend of increasing entropy, the greater the entropy, the more homogeneous the load, and when the load of cluster system completely uniformly distributed, the entropy value reaches the maximum at the same time. That is, to find a probability distributions of p_i—make the distribution evenly as possible—to get the maximum of H(t) under constrain condition.

4.2. The Properties

Through the definition above, we can conclude that the entropy of a homogeneous cluster has the following properties:

Property 1. The load balancing is always moving with the trend of increasing entropy. In other words, the changing trends of the entropy value determine the load-balancing.

As the entropy can be used to indicate the randomness of material, an increase of the entropy represents that the material tends to be stable. The target of load-balancing is the even distribution, so the increase of the entropy can achieve the target, which means that the changing trends of the entropy value can determine the load-balancing distribution.

Property 2. The entropy will reach its maximum if and only if the load is completely balanced, that is, the state of maximum entropy is the most balanced state of load.

From Property 1 we know that the load balancing is always moving with the trend of increasing entropy, so when the load completely balanced, the entropy reached its maximum.

Property 3. When the entropy reaches its maximum, the execution time of the task reaches the minimum.

From the definition of entropy, when the relative load factors are the same in each node, the entropy reaches its maximum. At the same time, the execution time of the program reaches its minimum.

Property 4. The change of the entropy is incremental. After it reaches its maximum and remains stable for a while, it will decrease.

At the starting stage of the system, the time when the load starts to be scheduled, the load distribution of the cluster is not balanced, so the value of the entropy is smaller. The load is assigned evenly to each server as time passes by, so the system reaches balance and the value of the entropy reaches the maximum. However, due to the difference of tasks, some servers will have completed their tasks while others are still running, which will destroy the balance. Then the load distribution of the system won’t be balanced, and the value of the entropy will decrease gradually.

Property 5. As the entropy increases, the maximum relative load factor of a homogeneous cluster decreases. If and only if the load is completely balanced, the entropy reaches its maximum.

Theorem 1. If the relative load factor is p₁,p₂,…,p_n, then the sufficient and necessary conditions of maximum entropy H(t) is p₁=p₂=⋯=p_n=1/n.

Proof. As ${\displaystyle {\sum }_{i=1}^n{p}_i}=1$, so we can use the Lagrange Multiplier Method to get the p_i of maximum entropy:

$$G\left(p_1,\dots ,p_n\right)=-{\displaystyle {\sum }_{i=1}^n{p}_i\ln p_i}+\lambda \left({\displaystyle {\sum }_{i=1}^n{p}_i}-1\right)$$

(14)

then take the partial respect of G to p_i, and set it to zero to obtain the equation as follows:

$$\frac{\partial G}{\partial p_i}=-\ln p_i-1+\lambda =0,i=1,2,\dots ,n$$

(15)

$$p_i=e^{\left(\lambda -1\right)}$$

(16)

because of ${\displaystyle {\sum }_{i=1}^n{p}_i}=1$, so:

$${\displaystyle {\sum }_{i=1}^n{p}_i}=1\Rightarrow n{p}_i=1\Rightarrow p_i=1/n$$

(17)

that is p₁=p₂=⋯=p_n=1/n, and the corresponding entropy is $-{\displaystyle {\sum }_{i=1}^n\left(1/n\right)\ln \left(1/n\right)}=\ln \left(n\right)$.□

Theorem 2. If the relative load factor is p₁, p₂,…,p_n, then the entropy can be expressed as H(p₁, p₂, …, p_n), so H(p₁, p₂, …, p_n) < H(p₁, p₂, …, p_i + δ, …, p_j ‒ δ, …, p_n) when 0 < δ ≤ (p_j−p_i)/2.

Proof. set y=H (p₁, p₂,…,p_i+x,…,p_j−x,…,p_n), then:

$$y={\displaystyle {\sum }_{k=1,k\ne i,j}^n{p}_k\ln \frac{1}{p_k}}+\left(p_i+x\right)\ln \frac{1}{p_i+x}+\left(p_j-x\right)\ln \frac{1}{p_j-x}$$

(18)

$$\frac{dy}{dx}=-\ln \left(p_i+x\right)+\ln \left(p_j-x\right)$$

(19)

when 0 < x ≤(p_j−p_i)/2, there is $\frac{dy}{dx}\ge 0$, if and only if the x is equal to (p_j−p_i)/2, the equality holds and the Theorem 2 certificate. □

Theorem 3. If the relative load factor is p₁, p₂,…, p_n, then the entropy can be expressed as H(p₁, p₂,…,p_n) For ∀p_i≤p_j, there is H(p₁, p₂,…,p_n)> H(p₁, p₂,…,p_i−δ,…,p_j+δ,…,p_n) when 0 <δ≤ p_i and δ≤(1−p_j).

Proof. set y=H(p₁,p₂,…,p_i−x,…,p_j+x,…,p_n), then

$$y={\displaystyle {\sum }_{k=1,k\ne i,j}^n{p}_k\ln \frac{1}{p_k}}+\left(p_i-x\right)\ln \frac{1}{p_i-x}+\left(p_j+x\right)\ln \frac{1}{p_j+x}$$

(20)

$$\frac{dy}{dx}=\ln \left(p_i-x\right)-\ln \left(p_j+x\right)$$

(21)

when 0 <δ≤ p_i and δ≤(1−p_j), there is $\frac{dy}{dx}\le 0$, the equality holds and the Theorem 3 certificate. □

Through the definition, properties and theorems above, we can realize that entropy is a good measure to judge the degree of load balancing and the MEM can accurately indicate the target of load balancing, so in this paper, a load balancing algorithm based on the MEM is proposed. It not only can make the system load balanced in a short period of time with respect to the trend of entropy increase, but also can make full use of server resources and avoid waste caused by the uneven distribution of the load.

5. Implementation of the Algorithm

In order to achieve the goal of load balance in a cluster system, the operation can be divided into two stages: the first stage is distributing the load equally to all servers in the cluster when doing the load dispatch, which can make the system achieve balance; the second stage is making partial adjustment after the load distribution on the servers, which means migrating the tasks on the overload server nodes to a lightly-loaded one. Then the system will achieve balance. Therefore, the following four questions should be solved:

• The collection and processing of load information on server nodes
• The selection of the scheduling policy
• The selection of the migration strategy
• The implementation of migration

In this paper, a new load balancing algorithm based on MEM in homogeneous clusters was put forward and the difficult problems above were solved. The solutions to the four problems will be described in detail below, and finally, a complete description of the algorithm will be given.

5.1. Collection and Processing of Load Information

This paper focuses on the variance of entropy. According to the definition of entropy, it is related to the relative load factor, which is the ratio of the load of the nodes to the total load of the system. The load can not only be calculated by the number of tasks, but also can be measured by the calculation of tasks. However, in the homogenous cluster system—when the calculation of tasks can be measured—it is better to use the total computation of tasks to reflect the load of the server node S_i than the number of tasks of node S_i in the server, so we chose the calculation of tasks as the measurement of the load for the server node in this paper. In order to calculate the value of entropy, we need to know the load of each server node. We need to synchronize, coordinate the nodes status information to the back-end services. If using traditional dynamic monitoring, it could cause a lot of traffic and increase the load of the system, so in this paper, we introduced a monitor node to centralize the collection of the load information, and then calculated the relative load factor p_i of each server node as well as the entropy H(t) of the current system. Finally, all the information we obtained should be fed back to the scheduler for load scheduling. In this way, each server node merely needs to transmit the load information to the monitor node for processing and feed back the information uniformly, which ensured the state synchronization between servers and reduced the traffic. Meanwhile, this avoids single points of failure caused by a single monitor node. With a hot-standby strategy, it can switch over to the standby monitor node when the main node failure, which will ensure the system keeps running normally.

5.2. Selection of the Scheduling Policy

There are many mature scheduling algorithms, such as Round-Robin Scheduling Algorithm, Least-Connection Scheduling Algorithm, Weighted Round-Robin Scheduling Algorithm, Destination Address Hashing Scheduling Algorithm and so on. The algorithm proposed in this paper is based on the MEM, which means scheduling based on the change of obtain the maximum entropy of the system. After the scheduler obtained the relative load factor of each server node and the entropy of the system from the monitor node, we first need to calculate the entropy changes according to the calculation of the scheduled tasks after the tasks have been scheduled to the server node, and then select a server node, whose entropy is increasing and whose increment of the entropy is the maximum, as the machine whose purpose is task scheduling to complete this schedule. In this way, the entropy of the system is increased with the maximum increment when every scheduling is processing, so that the entropy increases to the maximum when we finish the task scheduling, and according to Property 2 above, the load of the system has achieved the most balanced state at the moment. This scheduling algorithm can make the system achieve a load balancing state in a comparatively short period of time so as to avoid wasting server resources.

5.3. Selection of the Migration Strategy

Due the differences of the tasks and the fact the times needed to complete the tasks are different, which means some tasks have completed while some other tasks are still performing, this leads to the change of the relative load factor of the server node, which will influence the entropy changes. According to Property 4, we know that the entropy will be reduced at this moment, which indicates that the load of the system becomes unbalanced at this moment. We need to reschedule the load to put it back into balance, such as using migration. However, the migration needs to take up system resources and time of the system, so if we do it without rules, it will do more harm than good, which will not only worsen the situation of the system load, but also will increase the burden on the system.

Therefore, the key point we have to focus on is when and how to do the migration. In this paper, we propose a load balancing algorithm based on the MEM by taking the entropy value as the judgment condition of whether to do the load migration.

For this, we design a threshold value H°of system entropy as the load migration critical condition and compare the current system entropy H(t)calculated by the monitor node with this threshold value H°. If H(t) is less than H°, it reflects that the load distribution of system is unbalanced, and the load migration is needed, which means transferring the tasks from high-load nodes to low-load nodes. Balancing the load of each server node the entropy value will increase, so as to realize the system load balance; on the country, if H(t) is greater than or equal to H°, it explains that the load of system is balanced, there is no need to do any migration. We can be seen that the key influencing factor for migration is the threshold value H° of the system entropy. If the threshold value H° is too low, it will reduce the chances of migration, and that will lead to an unbalanced load on system nodes, which will cause the tasks on the high-load nodes to not be processed, while there is no task for the low-load nodes to handle. As a result, there will be a waste of system resources, and even a system crash caused by the overload; or otherwise, if the threshold value H° is too high, the migration will happen frequently, and since the migration needs to consume system resources, this will degrade the system performance.

5.4. Implementation of the Migration

The monitor node calculates the relative load factor by obtaining the current load information of each server node, so as to calculate the current entropy value H(t) of the system, which will be compared with the threshold value H°. Then the results may feed back into the scheduler, which determines whether to do the migration, the tasks that need migration and the migration target server. The migration is also based on the entropy value, ensuring that the entropy of the system will increase after the migration so as to achieve load balance, otherwise, the migration is not executed. This is an NPC problem [17], so we cannot find a common formula to solve it, so we use the following conventions:

• The tasks are always migrated from high-load nodes to low-load nodes, but not vice versa. It means that the migration is always toward the increasing trend of system entropy value.
• The tasks with too small an amount of calculation are beyond the selection scope of the migration because the migration needs to use system resources and execution time Maybe the time taken to do the migration is far beyond the execution time of tasks. This will cause a waste of system resources and time.

Therefore, whether the system does the migration depends on whether the system entropy value increased and the load-balanced situation is improved significantly after the migration.

5.5 Description of the Algorithm

The main description of this algorithm is listed as follows:

• Step 1. According to the information collected, we can calculate the load L_k and relative load factor p_i of each server node as well as the average relative load factor, so as to obtain the system’s current entropy value. Then, we turn to Step 2;
• Step 2. To compare the system’s current entropy value H(t) with the threshold value H° we do the following:

  • If the H(t) is less than H°, it means that the system load is unbalanced and needs migration. For the server nodes whose relative load factor p_i of each server node is greater than or equal to the average relative load factor p°, the relative load factor p_i should be sorted in descending order to form a server queue Q_s. That is the server queue which needs to do the load migration; for the other server nodes whose relative load factor p_i of each server node is less than the average relative load factor p°, the relative load factor p_i should be sorted in ascending order to form a server queue Q_t. That is the server queue which can accept the load. Then we turn to Step 3 to do the migration;
  • If the H(t) is greater than or equals to H°, it shows that the system load is comparatively balanced and it is unnecessary to do the migration. We see if there is any new load to be scheduled and if there is, then we turn to Step 4 and do the scheduling operation; otherwise, return to Step 1 and calculate the next moment;
• Step 3. To traverse the queue Q_s and Q_t, and take out the nodes S and T to migrate the task on node S to node T, ensuring that the entropy of the system will increase after the migration. For the node S, the operation will be continued until the relative load factor p_i of each server node is less than the average relative load factor p°, then we remove the node S from the queue Q_s; for the node T, the operation will be finished when the relative load factor p_i of each server node is greater than or equal to the average relative load factor p°, then we remove the node T from the queue Q_t. The migration won’t be finished until any queue is empty, and then we go back to Step 1;
• Step 4. To schedule the new tasks, and form a server queue Q sorted by the relative load factor p_i in ascending order, scanning this queue and finding out the node S whose entropy increased and is the maximum after the scheduling. If it exists, then the task is scheduled to the node S to finish the task scheduling, and then we return to Step 1.

6. Experiments and Results

In order to verify the effectiveness and feasibility of the algorithm proposed in this paper, we designed the following experiments to compare the Maximum Entropy Methods-based load balancing algorithm in homogeneous cluster (MEMBLB) with the Task Threshold Value-based load balancing algorithm (TTVBLB) and the Genetic Algorithm-based load balancing algorithm (GABLB).

6.1. Environment of the Experiments

The tools we used to create the environment of the experiments are as below:

• OpenStack: OpenStack is an open source cloud management platform, which provides an easy way to create, manage, and release virtual machines. As is known to all, no two leaves are identical in the world, so it is difficult to create a completely homogeneous cluster. We solved this problem by using OpenStack to create some near-identical virtual machines with the same image. There are three servers with the same configuration of 2.4GHz CPU, 8G RAM and Ubuntu 12.04.
• Haproxy: Haproxy is an open source traditional load balancing procedure. We have changed the procedure to use the above two load balancing algorithms and compare them in the experiments.
• KVM: KVM is a virtualization platform, which provides some programmatic APIs to create, migrate and destroy virtual machines. In this experiment, OpenStack used KVM to create the virtual machines.

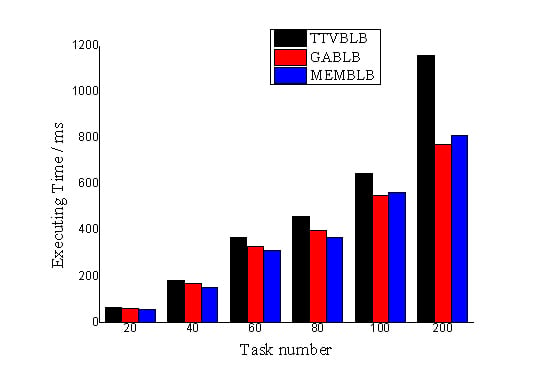
6.2. Results of the Experiments

Experiment 1. Comparison of MEMBLB and TTVBLB on the degree of load balancing and load migration for multiple tasks under the case of the same node number.

In this experiment, the experiment object are fifty tasks selected randomly from the system, and the environment is a homogeneous cluster formed by five virtual machines, created by OpenStack with the same image. They had the same configuration and were indicated by the letters A, B, C, D and E.

This experiment is divided into two steps: firstly, we adopt the traditional algorithm TTVBLB to schedule and load balance, and record the load amount of each of the system’s servers after reaching balance, and then calculate the corresponding entropy; secondly, we do the same task using the MEMBLB algorithm mentioned in this paper; finally, we compare the results of the two groups and analyze them.

Among a large number of experiments, this paper selects the most representative one to explain.

Table 1. The load of each node after scheduling with the two algorithms.

Nodes	The load after scheduling
	TTVBLB	MEMBLB
Node A	11	10
Node B	11	13
Node C	16	12
Node D	15	15
Node E	10	13
Entropy	1.5914	1.6010

shows the load of each server after scheduling with the two algorithms, the MEMBLB algorithm and the traditional TTVBLB algorithm. For convenience this paper calculates the tasks instead of the load.

By applying to the definition of entropy, that is $H\left(t\right)={\displaystyle {\sum }_{i=1}^n\left[p_i\ast \ln \left(1/p_i\right)\right]}$, the current entropy of system can be calculated, and the entropy with the TTVBLB algorithm is 1.5914, while the entropy with the MEMBLB algorithm is 1.6010. According to the properties of the entropy, we know that the scheduling with the MEMBLB algorithm can make the system load more balanced than the one with the traditional algorithm, that is, the MEMBLB algorithm can make the system load tend to be balanceable faster than the TTVBLB algorithm.

Table 2. The load of each node after migration with the two algorithms.

Nodes	the load after migration
	TTVBLB	MEMBLB
Node A	13	12
Node B	11	13
Node C	13	12
Node D	13	13
Node E	13	13
Entropy	1.6074	1.6087

shows the load of each server after migration with the two algorithms.

The current entropy of the system can be calculated, and the entropy with the TTVBLB algorithm is 1.6074, while the entropy with the MEMBLB algorithm is 1.6087. By comparing with the above data, we see that both algorithms can make the system entropy increase after migration, which means that the system load is distributed more evenly after migration. Moreover, the entropy value with the MEMBLB algorithm is greater than the one with the TTVBLB algorithm, showing that the MEMBLB algorithm can make the system load balancing more effective than the TTVBLB algorithm.

Experiment 2. Comparison of MEMBLB and TTVBLB on the executing time of the programs, the efficiency and the change of system entropy during an application's execution for the same large computing task under the case of different node number.

The feature of the computing tasks is to start on one node in the cluster, and when the load is imbalanced, it would be decomposed into multiple small tasks, which will be transferred to other nodes to perform, so that it makes the system load balanced, and when the load is balanced, the tasks can be executed directly without decomposing. First, we compared the changing execution time with node number, which is 1–20. When there’s only one node, the program is carried out serially; and if there’s more than one node, there is a node for scheduling and other nodes for computing. The results are shown in Figure 1:

As can be seen from Figure 1, that with the increasing number of nodes in the cluster, the program execution time is reduced. When there are two nodes, it means that there is only one computing node, and the program execution time is slightly longer than the serial program because of the cost of the load balancing algorithm. With an increasing number of nodes, there is more migration and the cost of load balancing increases, but the increasing number of nodes does not affect the program execution time much, which even does not rise and instead falls. When the node number is 16, the MEMBLB algorithm’s program execution time has reached its lowest point (10.4 ms), while the TTVBLB algorithm’s program execution time is 11.8 ms, so the MEMBLB algorithm will reduce the minimum execution time by approximately 11.9%.

Secondly, Figure 2 shows how the efficiency of the two algorithms changes with node number. It is seen that the MEMBLB algorithm’s maximum efficiency is 0.83, while the TTVBLB algorithm’s is 0.74, so the MEBLB algorithm raises the maximum efficiency by about 22.9%.

Then, we focus on how the system entropy value changes with time during the application’s execution. There is a cluster with 10 nodes, one node for scheduling and the other nine for computing. We record the change of system entropy of the scheduling node during system execution, which means recording the entropy value before and after each migration. The experimental results shown in Figure 3 as below:

As can be seen from Figure 3, at the beginning the system entropy is 0 because the task is on only one node, so there is no load migration. After the decomposition, the task will generate multiple sub-tasks running on multiple nodes, so the entropy value increases. What’s more, the entropy is further increased and close to the maximum value ln9=2.197 after the migration, then the system entropy remains stable at about 2.17. When the program is coming to an end, the entropy value fell sharply because the tasks are completed, and the load on the node is very small, so there is no load migration at this moment.

Experiment 3. Comparison of the three algorithms regarding the execution time of the programs and the efficiency under the case of different task number.

At first, we compared how the execution time changes with task number, which is 20–200. The results are shown in Figure 4

As can be seen from Figure 4, the TTVBLB algorithm’s program execution time is always the longest one, and the gap between them widens with task number. When there are fewer tasks, the MEMBLB algorithm’s program execution time is shorter than that of the GABLB algorithm. However, as the number of tasks increases, the MEMBLB algorithm’s program execution time is longer than that of the GABLB algorithm, but not that much more. Secondly, Figure 5 shows how the efficiency of the three algorithms changes with task number. It is seen that the MEMBLB algorithm’s efficiency is always the highest, which means that the MEMBLB algorithm can make the system load balancing more effectively than the other two algorithms.

6.3. Analysis of the Results

In order to better illustrate the effectiveness and feasibility of this algorithm proposed in this paper, we used the variance analysis method to analyse the experimental results. The variance is used to evaluate the random variable and its mathematical expectation (average) deviation. The greater the variance, the higher the degree of deviation; the smaller the variance, the lower the degree of deviation. Thus, we can use the variance to measure the degree of load balancing. Let’s define load variance as the variance of load amount among servers:

$$v={\displaystyle {\sum }_{i=0}^p{\left(l_i-m\right)}^2}$$

(22)

where p is the number of servers, l_i is the load amount of each server, and m is average load:

$$m=\left(1/p\right){\displaystyle {\sum }_{i=0}^p{l}_i}$$

(23)

The smaller the load variance, the lower the degree deviation and the higher the degree of load balancing; while the greater the load variance, the higher the degree deviation, the lower the degree of load balancing. In the ideal situation, the load variance is zero when the load becomes totally balanced. Here we use load variance to validate the result of the experiments.

As revealed in Table 1, from the result of Experiment 1 can be concluded that the value of the load by using the TTVBLB algorithm is $m=\left(1/p\right){\displaystyle {\sum }_{i=0}^p{l}_i}=12.6$, and the load variance is $v={\displaystyle {\sum }_{i=0}^p{\left(l_i-m\right)}^2}=29.2$; while the value of the load by using the MEMBLB algorithm is $m=\left(1/p\right){\displaystyle {\sum }_{i=0}^p{l}_i}=12.6$, and the load variance is $v={\displaystyle {\sum }_{i=0}^p{\left(l_i-m\right)}^2}=13.2$.

By comparing these two results, we can conclude that the load variance obtained by using the MEMBLB algorithm is less than that of the TTVBLB algorithm, which can demonstrate that the degree of load balancing achievable using the MEMBLB algorithm is higher than that of the TTVBLB algorithm.

As revealed in Table 2, we can calculate that the value of the load by using the TTVBLB algorithm is $m=\left(1/p\right){\displaystyle {\sum }_{i=0}^p{l}_i}=12.6$, and the load variance is $v={\displaystyle {\sum }_{i=0}^p{\left(l_i-m\right)}^2}=3.2$; while the value of the load by using the MEMBLB algorithm is $m=\left(1/p\right){\displaystyle {\sum }_{i=0}^p{l}_i}=12.6$, and the load variance is $v={\displaystyle {\sum }_{i=0}^p{\left(l_i-m\right)}^2}=1.2$.

By comparing these two results, we can conclude that the load variance achieved using the MEMBLB algorithm is less than that of the TTVBLB algorithm, which can demonstrate that the degree of load balancing using the MEMBLB algorithm is higher than that of the TTVBLB algorithm. In addition, by comparing with the above data, both algorithms can make the load variance decrease after migration, which means that the system load is distributed more evenly after migration.

Through the comparison and analysis above, we can draw the conclusion that it is feasible to use the entropy as a metric of the degree of load balancing, and the MEMBLB algorithm is an effective load balancing algorithm. As revealed in Figure 4, as the tasks increase, the MEMBLB algorithm’s program execution time is longer than that of the GABLB algorithm but not that much more, so we should apply the GA to the MEMBLB algorithm in a future version so that it can do better. Moreover, as this algorithm is executed on a homogeneous cluster without consideration of the heterogeneity of servers, fault detection and recovery and the design of network topology, it cannot satisfy well the demands of a practical application environment. Thus, the next step in the work is optimizing this algorithm in order to extend it to heterogeneous clusters.

7. Conclusions

By introducing the concept of entropy in thermodynamics into load balancing, this paper proposes a load balancing algorithm in homogeneous clusters based on the Maximum Entropy Method, gives the theoretical model and the basic properties of system entropy, uses the entropy as a measure for the degree of load balancing, and schedules and migrates in accordance with the entropy change to make the system achieve the goal of load balancing faster and better. Meanwhile, this paper compares the proposed algorithm with other traditional algorithms, showing that the new algorithm is better than the traditional algorithms on the time and degree of system load balancing, which indicates that the new algorithm is workable to a certain extent to balance the load in homogeneous clusters. However, since the algorithm is executed on homogeneous clusters without consideration of the heterogeneity of servers, fault detection and recovery, the design of network topology and so on, there are still many problems that have to be solved in practical application environments. Therefore, the next task of this work should focus on the optimization of this algorithm to enable it to adapt to the situation of heterogeneous clusters and, as a result, achieve a load balancing algorithm with wide applicability.