Comparative Study of Entropy Sensitivity to Missing Biosignal Data

Abstract

Entropy estimation metrics have become a widely used method to identify subtle changes or hidden features in biomedical records. These methods have been more effective than conventional linear techniques in a number of signal classification applications, specially the healthy–pathological segmentation dichotomy. Nevertheless, a thorough characterization of these measures, namely, how to match metric and signal features, is still lacking. This paper studies a specific characterization problem: the influence of missing samples in biomedical records. The assessment is conducted using four of the most popular entropy metrics: Approximate Entropy, Sample Entropy, Fuzzy Entropy, and Detrended Fluctuation Analysis. The rationale of this study is that missing samples are a signal disturbance that can arise in many cases: signal compression, non-uniform sampling, or data transmission stages. It is of great interest to determine if these real situations can impair the capability of segmenting signal classes using such metrics. The experiments employed several biosignals: electroencephalograms, gait records, and RR time series. Samples of these signals were systematically removed, and the entropy computed for each case. The results showed that these metrics are robust against missing samples: With a data loss percentage of 50% or even higher, the methods were still able to distinguish among signal classes.

1. Introduction

A number of types of entropy estimation measures and their possible applications have been reported in the scientific literature in recent years. These nonlinear metrics have been employed in multiple scientific fields for the analysis of time series, yielding better results than other conventional methods [1–3].

There is a myriad of such applications in the specific biomedical signal framework because biological systems are great entropy generators [4]. In this context, entropy estimates have been successfully used in cardiology [5–9], neurology [10–15], neonatology [16–20], and pneumology [21,22], among others.

An ongoing characterization effort has been lately undertaken to gain a better understanding of signal entropy measures and their properties [4]. Works such as [23,24] have studied the influence of parameters like signal length or thresholds. The studies reported in [25–27] analyzed their essential features in terms of bandwidth and signal complexity. Garcia-Gonzalez [28] and Molina-Pico [29], assessed robustness against signal outliers.

Nevertheless, some issues related to entropy measures characterization have not been addressed yet. We describe in this paper a characterization scheme aimed at assessing the influence of missing data on entropy estimates. Missing data are not unusual in biomedical signals. Time series are vulnerable to uncontrolled factors such as noise [30] or outliers, but other technical processes may cause missing points such as wireless or network data transmission [31,32], signal compression [33,34], non-uniform sampling, trace segmentation [35], or resampling.

This study is focused on four of the most used regularity metrics in the context of biomedical signal processing: Approximate Entropy (ApEn), Sample Entropy (SampEn), Fuzzy Entropy (FuzzyEn), and Detrended Fluctuation Analysis (DFA). Other metrics have been evaluated in previous studies [36]. Our work assesses the robustness of the entropy measures enumerated above against missing data in terms of signal discrimination potential. In particular, we aimed to assess the possible deterioration of the pathology detection capability of these measures. This characterization study is illustrated by considering detection of signal classes from a diverse biosignal population: electroencephalogram signals (EEG), gait dynamics records, and RR interval time series.

The remainder of this article is structured as follows. In Section 2, we introduce the four entropy metrics to be characterized in terms of robustness against data loss. We describe in Section 3 the experiments and the dataset employed. In Section 4, the statistical results are presented, as a function of the data loss ratio. In Section 5, we interpret our findings. Finally, the conclusion section summarizes the main results of the study.

2. Method

The experimental dataset was processed using ApEn, SampEn, FuzzyEn and DFA. Each metric was computed for each record, and for different data loss levels, within a signal classification scheme. The signal segmentation probability was computed. The objective of the method was to assess whether these measures were stable as a function of the data loss ratio.

Specifically, the measures of ApEn, SampEn, FuzzyEn and DFA were computed for every record in the experimental set for data loss percentages of 0% (baseline), 10%, 30%, 50%, 70%, and 90%. There were 100 realizations for each signal. Each sample could only be deleted once. The spare samples were removed using two approaches:

• Uniform sample removal. This scheme accounts for data loss that might occur during wireless or network data transmission, or acquisition saturation. The number of samples to remove (X) was set as a function of a percentage proportional to the total data series length. The removal started at a sample chosen randomly. Therefore, an epoch of X consecutive samples commencing at a random time was removed in this case. The step X was defined in accordance with the specified sample loss percentage.
• Random sample removal. This scheme accounts for data loss that might occur during non-uniform sampling, trace segmentation, or lossy compression. The X samples to be removed were selected according to a random distribution.

The resulting entropy values were used in a statistical comparative analysis to find out if the downsampled signals could still be segmented as they were for the baseline case. Data Gaussianity was tested before applying the parametric t-test. The p-value threshold was set to 0.05.

Two populations were compared with this test, corresponding to the control and the epileptic classes in EEG signals, the Pre-Treatment (PT) and the On-Treatment (OT) records in RR series, and the pathologic versus the control groups in gait signals. A hypothesis testing with this p-value indicates that the two classes are found different by the entropy metrics.

Given an input time series u(n) of length N, with n = 0, 1, … , N − 1, the algorithms to calculate ApEn, SampEn, FuzzyEn, and DFA metrics can be described as follows.

2.1. ApEn

ApEn is a family of statistics first proposed in [9]. Despite its well-known weaknesses, such as counting self-matches and being very dependent on signal length [8,37,38], ApEn is still able to unveil significant clinical information from biomedical records [25,39]. It is probably the entropy estimator most used in the context of biosignal classification.

The mathematical definition of ApEn is as follows: Let x(i) be an epoch of m consecutive values of u(n) taken at the i^th point [9], subject to N ≥ 10^m: x(i) = [u(i), u(i + 1), …, u(i + m − 1)]. The input parameter m is usually recommended to be 2 or 3 in order to obtain a good statistical validity [9,38]. We used m = 2. Let d(i, j) be a dissimilarity measure between two runs, namely:

$$d(i,j)=d(x(i),x(j))=\underset{k}{{\displaystyle max}}\{\left|x(i+k-1)-x(j+k-1)\right|\}k=1,\dots ,m$$

The input parameter r represents a filter threshold in terms of signal variance σ_u. In practice, r is chosen to be between 0.1σ_u and 0.25σ_u. Smaller values would yield numerically unstable conditional probabilities and larger values could result in too much detail information lost due to filter coarseness [9]. We used r = 0.15σ_u.

Defining a dissimilarity thresholding function y(i) as:

$$y(j)=\{\begin{array}{cc}1& d(i,j)\le r\\ 0& d(i,j)>r\end{array}$$

(1)

and a counting function $C_i^m(r)$ as:

$$C_i^m(r)=\frac{1}{N-m+1}{\displaystyle \sum _{j=1}^{N-m+1}y(j)}$$

(2)

ApEn(m, r, N) can then be estimated as the likelihood ratio:

$$\text{ApEn}(m,r,N)={\mathrm{\Phi }}^m(r)-{\mathrm{\Phi }}^{m+1}(r)$$

(3)

where Φ^m(r) is computed as follows:

$${\mathrm{\Phi }}^m(r)=\frac{1}{N-m+1}{\displaystyle \sum _{i=1}^{N-m+1}\ln \{C_i^m(r)\}}$$

(4)

2.2. SampEn

SampEn was first proposed by Richman and Moorman in 2002 [8]. It was devised as a solution to reduce the ApEn bias due to counting self-matches and therefore it is supposed to yield a more robust statistic. SampEn is a measure that estimates the regularity of a time series by computing the negative logarithm of the conditional probability that two sequences, which are similar for m points, remain similar for m + 1 points [8,40].

SampEn is largely independent of the record length and exhibits relative consistency under circumstances where ApEn does not. SampEn agrees much better than ApEn statistics with theory for random numbers over a broad range of operating conditions [6–8].

The algorithm to compute SampEn is simpler than that of ApEn. The first steps are the same, but Equation (2) becomes:

$$C_i^m(r)=\frac{1}{N-m-1}{\displaystyle \sum _{{}_{j\ne i}^{j=1}}^{N-m}y(j)}$$

being m and r the same parameters introduced for ApEn. The value for y(j) is computed as defined in Equation (1), and Equation (4) turns into:

$${\mathrm{\Phi }}^m(r)=\frac{1}{N-m}{\displaystyle \sum _{i=1}^{N-m}{C}_i^m(r)}$$

(5)

Finally, SampEn(m, r, N) is obtained as:

$$\text{SampEn}(m,r,N)=\ln ({\mathrm{\Phi }}^m(r))-\ln ({\mathrm{\Phi }}^{m+1}(r))$$

(6)

2.3. FuzzyEn

FuzzyEn was first proposed in [41] in order to characterize surface electromyograms time series regularity and overcome the poor statistical stability in ApEn and SampEn [41,42]. FuzzyEn imported the idea of “fuzzy sets” proposed by Zadeh [43]. FuzzyEn introduces a membership function, μ_Z(x) that evaluates the degree in which a pattern belongs to a class Z. The closer the value to 1, the higher the membership grade of pattern x belonging to that class.

The membership function proposed by Chen [41] is an exponential function. Any such function must be continuous and convex, so that the similarity does not change abruptly [41,42].

The FuzzyEn algorithm is similar to that of SampEn [8]. The main differences include the membership function used to compute the matches to be found and the way the runs are defined. For the input sequence u(n) introduced in Section 2.1, the runs of m points now become:

$$x(i)=[u(i)u(i+1)\dots u(i+m-1)]-u0(i)$$

(7)

where u0(i) represents the baseline of x(i) and is estimated as follows:

$$u0(i)=\frac{1}{m}{\displaystyle \sum _{j=0}^{m-1}u(i+j)}$$

(8)

The distance between two runs d(i, j) is computed as described for ApEn and SampEn. Next, given q and r, the similarity $D_{ij}^m$ between x(i) and x(j) is calculated according to:

$$D_{ij}^m(q,r)=\mu (d_{ij}^m,q,r)$$

(9)

where $\mu (d_{ij}^m,q,r)$ is the membership function given by:

$$\mu (d_{ij}^m,p,r)=exp(-{(d_{ij}^m)}^n/r)$$

(10)

The similarity degree $D_{ij}^m$ computed for FuzzyEn is like the value y(n) computed for ApEn and SampEn. The following step is to obtain $C_i^m(r)$ as defined for SampEn where y(n) is replaced by $D_{ij}^m$, and calculate the conditional probabilities in the same way as for SampEn according to Equation (5).

$${\varphi }^m(q,r)=\frac{1}{N-m}{\displaystyle \sum _{i=1}^{N-m}{C}_i^m(r,n)}$$

(11)

$$C_i^m(q,r)=\frac{1}{N-m-1}{\displaystyle \sum _{j=1,j\ne i}^{N-m}{D}_{ij}^m}$$

(12)

Finally, FuzzyEn is computed as defined in Equation (6) from the previous values obtained. The parameters m and r are defined as in ApEn or SampEn [41], but q has to be defined. The parameter q accounts for the width of the exponential function and it is usually set to a small integer value greater than 1 in order to avoid the information loss due to wider exponential functions. Typically q = 2 [41,42,44].

2.4. Detrended Fluctuation Analysis (DFA)

DFA quantifies the regularity of a time series by detecting long range correlations embedded in a nonstationary time series [5]. As it only considers the fluctuations from local trends, DFA is capable of avoiding the spurious detection of apparent long range correlations that are nonstationary artifacts. However, it is also sensitive to series length N. When time series are short, DFA can exhibit a fluctuating behavior [5,13,45].

DFA is computed as a modified root mean square of a random walk. The first step of the algorithm is to generate the random walk [13] by integrating the input sequence:

$$U(k)={\displaystyle \sum _{i=0}^{k}u(i)}-\overline{u},\text{with}k=0,1,\dots ,N-1$$

(13)

where $\overline{u}=\frac{1}{N}{\displaystyle \sum _{j=0}^{N-1}u(j).}$

The input sequence u(n) is divided into non-overlapping runs of length L. A linear fit is used to approximate this sequence in each window W_j, j = 1, …, M. The local trend at window W_j is denoted $U_{W_j}(k)$. This local trend is subtracted from the integrated series $U(k)-U_{W_j}(k)$. A mean square fluctuation of the integrated and detrended time series can then be computed as described in [5]:

$$F(L)=\sqrt{\frac{1}{N}{\displaystyle \sum _{k=0}^{N-1}{(U(k)-U_{W_i}(k))}^2}}$$

(14)

These calculations are repeated for a set of window lengths. Let L = {L₁, L₂…L_i…L_n} be a windowing length sequence. The minimum L_i value corresponds to the order of the DFA plus two samples. The maximum value depends on the approach used. In [5], the maximum value is the length of the signal (N). Others such as [45] take it as N/4 and [10] uses the value of N/10. Typically, F_L increases with the window length.

If a time series is self-similar, a relationship indicates the presence of a power law scaling F_L ∝ L^α. The value of α accounts for the correlation properties of the data. The DFA coefficient α can be obtained as the slope of the line fit on the log–log plot of F_L as a function of L [5]. Large values of α denote smooth time series. An example is depicted in Figure 1.

The coefficient α usually ranges from 0 to 2 [10]. Three major intervals may be defined:

• For 0 ≤ α ≤ 0.5: The time series contains power law correlations but of different type.
• For 0.5 < α ≤ 1.0: The time series contains persistent long range power law correlations.
• For α > 1.0: There are correlations in the time series but nothing is known about their nature.

The windowing sequence L in this work has been chosen to include 50 equispaced values in the logarithmic scale between L_i minimum and N/4. Those logarithmic lengths that yield the same integer values have been removed.

3. Experimental Dataset

3.1. EEG Dataset

The EEG records were drawn from the public database of the Clinic of Epileptology, Bonn University, Department of Neurophysics [14]. The records of this database were obtained from continuous multichannel EEGs, cut out to remove artifacts. Five EEG classes, denoted from A to E, were available. Class A corresponds to surface EEG recordings acquired on five healthy volunteers relaxed in an awake state with eyes open. The electrodes were placed using standard locations. In class B, the same conditions apply except that in this case eyes were closed. Sets C, D and E correspond to EEGs of presurgical diagnosis of five epileptic patients after resection of one of the hippocampal formations. Records in D were drawn from the epileptogenic zone, while those in set C were recorded from the hippocampal formation. Both classes D and C contain only activity during seizure free intervals, whereas records in set E contain only seizure activity.

The signal sampling rate was 173.61 Hz, using a 12 bit analog-to-digital converter. The duration of each record was 23.6 s (4096 samples). Each class contains in total 100 single channel EEG segments. Figure 2 shows the EEG and the power spectral density (PSD) for one representative signal for each data group of the database.

Two new signal groups were considered for the experiments: control (original types A and B), and pathologic (original types C, D, and E). The objective was to assess the capability of these measures to segment between signals that conceptually correspond to healthy and pathologic subjects, as would be the case in a clinical analysis.

3.2. RR Interval Time Series Dataset

The RR records were drawn from the public Cardiac Arrhythmia Suppression Trial (CAST) database [46]. This database consists of 1725 post-acute myocardial infarction patients that were randomized to have three times daily either a placebo, encainide, flecainide, or moricizine [47–49]. Only encainide signals were used in this work.

For completeness, only 734 recordings of length 1000 samples constitute the experimental RR record database [50]. There are three groups of records in this set for the three medications given to the subjects. The name of each record includes a prefix to account for the type of medication: e, f, and m, respectively, and a suffix to indicate if medication was given, b (on-therapy OT records), or not, a (pre-therapy PT records). The groups to be segmented in the experiments were precisely the PT and the OT records within signal types e, f, and m.

3.3. Gait Dynamics Records Dataset

The gait dynamics records were drawn from the neuro-degenerative disease database [46]. It consists of 64 signals from which 16 are healthy control subjects, 15 suffer from Parkinson’s Disease (PD), 20 from Huntington’s Disease (HD), and 13 from Amyotrophic Lateral Sclerosis (ALS).

Initially, data were obtained using force transducers, where the values were proportional to the pressure under the foot. From these series, footfall times could be estimated [51,52].

Each record is named after the subject class (hunt, park, als, or control), followed by a number. Each record has four associated files: header, left foot signal, right foot signal, and derived time series. This last time series includes a number of subrecords, but for simplicity in this work we only analyzed right stance intervals measured as a stride percentage. The objective of the segmentation was to assess if the entropy metrics were able to distinguish pathologic signals hunt, park and als, from control.

4. Results

All the experimental records in the dataset underwent different ratios and types of sample loss as described in Section 2, and their entropy metrics were computed in each case. These metrics were then used in a statistical test to assess the differences among groups. In case of significance, the metric was considered able to segment signals even on undersampled data. Otherwise, the metric was considered not robust enough for the application. The specific quantitative results are described next for each experiment.

4.1. Random Sample Removal Results

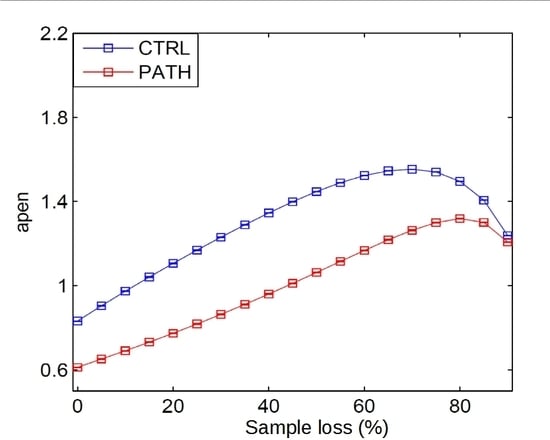
The results obtained for random sample removal using EEG, RR interval time series, and gait dynamics (percentage of Right Stance Interval in Double Support Interval for ALS, PD, HD) records, are shown in

Table 1. Results obtained for EEG signals rearranged in control and epileptic classes, using a random sample removal approach. Values in bold characters correspond to cases where the associated entropy measure was not able to distinguish between the two groups.

Metric	0%	10%	30%	50%	70%	90%
ApEn	p = 0.001	p = 0.001	p = 0.001	p = 0.001	p = 0.001	p = 0.001
SampEn	p = 0.001	p = 0.001	p = 0.001	p = 0.001	p = 0.001	p = 0.001
DFA	p = 0.001	p = 0.001	p = 0.001	p = 0.074	p = 0.004	p = 0.006
FuzzyEn	p = 0.001	p = 0.001	p = 0.001	p = 0.001	p = 0.001	p = 0.001

–

Table 5. Results obtained for pathologic HD gait records versus control records, using a random sample removal approach. Values in bold characters correspond to cases where the associated entropy measure was not able to distinguish between the two groups. NA corresponds to cases where not enough samples were available for the calculations.

Metric	0%	10%	30%	45%	70%	90%
ApEn	p = 0.001	p = 0.001	p = 0.001	p = 0.001	p = 0.001	p = 0.001
SampEn	p = 0.001	p = 0.001	p = 0.001	p = 0.001	p = 0.001	p = 0.001
DFA	p = 0.001	p = 0.842	NA	NA	NA	NA
FuzzyEn	p = 0.001	p = 0.001	p = 0.001	p = 0.001	p = 0.001	p = 0.001

respectively.

4.2. Uniform Sample Removal Results

The results obtained for uniform sample removal using EEG, RR interval time series, and gait dynamics records (ALS, PD, HD), are shown in

Table 6. Results obtained for EEG signals rearranged in control and epileptic classes, using a uniform sample removal approach. Values in bold characters correspond to cases where the corresponding entropy measure was not able to distinguish between the two groups.

Metric	0%	10%	30%	50%	70%	90%
ApEn	p = 0.001	p = 0.001	p = 0.001	p = 0.001	p = 0.001	p = 0.001
SampEn	p = 0.001	p = 0.001	p = 0.001	p = 0.001	p = 0.001	p = 0.001
DFA	p = 0.001	p = 0.001	p = 0.001	p = 0.001	p = 0.001	p = 0.001
FuzzyEn	p = 0.001	p = 0.001	p = 0.001	p = 0.002	p = 0.001	p = 0.002

–

Table 10. Results obtained for pathological gait records from HD patients versus control records (percentage of right stance interval measures in double support interval), using a uniform sample removal approach. Values in bold characters correspond to cases where the corresponding entropy measure was not able to distinguish between the two groups. NA corresponds to cases where not enough samples were available for the calculations.

Metric	0%	10%	30%	45%	70%	90%
ApEn	p = 0.001	p = 0.001	p = 0.001	p = 0.001	p = 0.001	0.056
SampEn	p = 0.001	p = 0.001	p = 0.001	p = 0.001	p = 0.001	p = 0.001
DFA	p = 0.001	p = 0.064	NA	NA	NA	NA
FuzzyEn	p = 0.001	p = 0.001	p = 0.001	p = 0.001	p = 0.001	p = 0.209

respectively.

5. Discussion

When samples are removed from biomedical records, the entropy metrics results change, as could be expected since the input data are modified. Nevertheless, the absolute value of these measures is not usually the goal of the calculations, but their relative value in comparison among classes.

In this regard, our study was devised to find out if the relative differences among such classes were kept even with some degree of data loss. This would enable the utilization of entropy estimators even under harsh conditions in normal procedures such as record compression, signal resampling, or data transmission applications.

From the results, in most cases, the measures were still able to distinguish between the two groups under test, since the test probability was p < 0.05. However, there are a few cases where the segmentation power was lost that have to be taken into account.

The negative cases are mainly in the experiments using SampEn and RR time series records, and FuzzyEn and gait records, whereas for the rest of the experiments, with some exceptions, the results were positive. This is due to, on one hand, the nature of the input series, and, on the other hand, the properties of the metric employed.

For narrowband signals, such as the RR records, removing samples could imply removing a fairly high amount of signal information. On the contrary, broadband signals such as EEGs can keep most of the information even with the removal of some samples (Gaussian noise-like). In addition, some records include spikes very different to the underlying data (RR series, gait records). These spikes, as studied in [29], also may have a great influence on the entropy metrics.

Regarding the performance of SampEn, it is very sensitive to the number of matches. Thus, its strength of omitting self-matches may turn into a weakness when only a limited number of matches are found, as happens in RR records. This is why SampEn does not find differences for RR records even in the baseline case. The use of random or uniform removal adds minor differences in terms of worse performance for random removal, as could be expected since the uniform approach is more regular.

FuzzyEn is another recent entropy estimator whose performance is expected to be superior to that of ApEn and SampEn. Nevertheless, it requires a third parameter q, the width of the exponential function, and therefore it is more difficult to customize for a specific purpose or signal. We had a similar experience with the improved versions of the same metrics, fApEn and qSampEn [53]. Such metrics perform very well, but in some cases they fail because the optimal parameter configuration is very difficult to find. That is what seems to happen with some gait records and FuzzyEn.

6. Conclusions

This work described a comparative study of the influence of signal sample loss in the segmentation capability of four of the most used entropy metrics in the biomedical framework: ApEn, SampEn, FuzzyEn and DFA. The performance of such metrics was illustrated using various records, including EEGs, RR interval time series, and gait dynamics records.

The performance of the methods suffices to be applied under conditions of significant data loss, if the objective is to segment among signal types. The relative differences are kept although the absolute entropy values change. This holds particularly true for broadband signals, such as the EEG. This conclusion enables the use of lossy data compression techniques or resampling methods for records that will later be processed using entropy estimators.

Of the four entropy measures studied, ApEn seems to be the most robust one, using a standard parameter configuration. Although SampEn is derived from the improvement of ApEn, there are a few cases where ApEn still outperforms SampEn, like the case introduced herein. If no differences are found in the baseline case, it is highly unlikely differences are found for higher ratios, although the relationship is not completely linear. DFA needs longer records and therefore it is not suitable for the epochs employed in this study. It also appears more sensitive to data loss than ApEn and SampEn.

In practical terms, with relatively low data loss ratios, it can be reasonably safe to employ ApEn, SampEn, or FuzzyEn, for classification tasks using biomedical records such as the ones tested, or with similar features. However, generalization is not possible because each metric and each biosignal may exhibit different behavior. Researchers should be advised to perform similar tests as the ones described in the present study if they suspect missing data is damaging their results, and choose entropy metrics and parameters carefully. With a proper configuration, it is very likely that most of the entropy estimators perform well even with severe data loss ratios.