Quantum Thermodynamics in Strong Coupling: Heat Transport and Refrigeration
Abstract
:1. Introduction
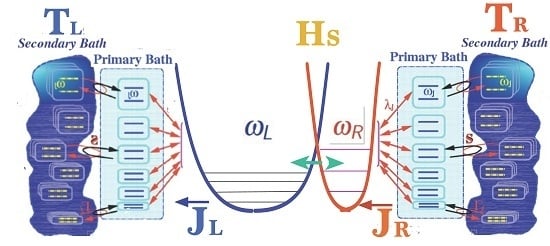
2. Basic Construction
3. Thermodynamical Aspects of the Surrogate Hamiltonian
Transport Dynamics
4. Heat Pump Operation
5. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| SSH | Stochastic Surrogate Hamiltonian |
| L-GKS | Lindblad–Goirini–Kossakowski–Sudarshan |
| COP | Coefficient of Performance |
References
- Kosloff, R. Quantum thermodynamics: A dynamical viewpoint. Entropy 2013, 15, 2100–2128. [Google Scholar] [CrossRef]
- Davies, E.B. Markovian master equations. Commun. Math. Phys. 1974, 39, 91–110. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119–130. [Google Scholar] [CrossRef]
- Gorini, V.; Kossakowski, A.; Sudarshan, E.C.G. Completely positive dynamical semigroups of N-level systems. J. Math. Phys. 1976, 17, 821–825. [Google Scholar] [CrossRef]
- Alicki, R. The quantum open system as a model of the heat engine. J. Phys. A Math. Gen. 1979, 12, L103. [Google Scholar] [CrossRef]
- Segal, D.; Nitzan, A.; Hänggi, P. Thermal conductance through molecular wires. J. Chem. Phys. 2003, 119, 6840–6855. [Google Scholar] [CrossRef]
- Segal, D.; Nitzan, A. Spin-boson thermal rectifier. Phys. Rev. Lett. 2005, 94, 034301. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.A.; Segal, D. Sufficient conditions for thermal rectification in hybrid quantum structures. Phys. Rev. Lett. 2009, 102, 095503. [Google Scholar] [CrossRef] [PubMed]
- Segal, D. Absence of thermal rectification in asymmetric harmonic chains with self-consistent reservoirs. Phys. Rev. E 2009, 79, 012103. [Google Scholar] [CrossRef] [PubMed]
- Katz, G.; Gelman, D.; Ratner, M.A.; Kosloff, R. Stochastic surrogate Hamiltonian. J. Chem. Phys. 2008, 129, 034108. [Google Scholar] [CrossRef] [PubMed]
- Katz, G.; Ratner, M.A.; Kosloff, R. Hot injection dynamics: Design mechanisms and ideas. J. Phys. Chem. A 2010, 115, 5833–5837. [Google Scholar] [CrossRef] [PubMed]
- Levy, A.; Kosloff, R. The local approach to quantum transport may violate the second law of thermodynamics. Europhys. Lett. 2014, 107, 20004. [Google Scholar] [CrossRef]
- Trushechkin, A.; Volovich, I. Perturbative treatment of inter-site couplings in the local description of open quantum networks. 2015; arXiv:1509.05754. [Google Scholar]
- Büttiker, M.; Imry, Y.; Landauer, R.; Pinhas, S. Generalized many-channel conductance formula with application to small rings. Phys. Rev. B 1985, 31, 6207–6215. [Google Scholar] [CrossRef]
- Segal, D. Two-level system in spin baths: Non-adiabatic dynamics and heat transport. J. Chem. Phys. 2014, 140, 164110. [Google Scholar] [CrossRef] [PubMed]
- Jing, J.; Segal, D.; Li, B.; Wu, L.A. Transient unidirectional energy flow and diode-like phenomenon induced by non-Markovian environments. 2015; arXiv:1507.00816. [Google Scholar]
- Xu, D.; Wang, C.; Zhao, Y.; Cao, J. Polaron effects on the performance of light-harvesting systems: A quantum heat engine perspective. New J. Phys. 2016, 18, 023003. [Google Scholar] [CrossRef]
- Schaller, G.; Krause, T.; Brandes, T.; Esposito, M. Single-electron transistor strongly coupled to vibrations: Counting statistics and fluctuation theorem. New J. Phys. 2013, 15, 033032. [Google Scholar] [CrossRef]
- Esposito, M.; Ochoa, M.A.; Galperin, M. Quantum thermodynamics: A nonequilibrium greenes function approach. Phys. Rev. Lett. 2015, 114, 080602. [Google Scholar] [CrossRef] [PubMed]
- Breuer, H.-P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Kosloff, R.; Levy, A. Quantum heat engines and refrigerators: Continuous devices. Annu. Rev. Phys. Chem. 2014, 65, 365–393. [Google Scholar] [CrossRef] [PubMed]
- Gelbwaser-Klimovsky, D.; Aspuru-Guzik, A. Strongly coupled quantum heat machines. J. Phys. Chem. Lett. 2015, 6, 3477–3482. [Google Scholar] [CrossRef] [PubMed]
- Katz, G.; Ratner, M.A.; Kosloff, R. Hot injection processes in optically excited states: Molecular design for optimized photocapture. J. Phys. Chem. C 2014, 118, 21798–21805. [Google Scholar] [CrossRef]
- Barra, F. The thermodynamic cost of driving quantum systems by their boundaries. Sci. Rep. 2015, 5, 14873. [Google Scholar] [CrossRef] [PubMed]
- Ludovico, M.F.; Lim, J.S.; Moskalets, M.; Arrachea, L.; Sánchez, D. Dynamical energy transfer in ac-driven quantum systems. Phys. Rev. B 2014, 89, 161306. [Google Scholar] [CrossRef]
- Bruch, A.; Thomas, M.; Kusminskiy, S.V.; von Oppen, F.; Nitzan, A. Quantum thermodynamics of the driven resonant level model. 2015; arXiv:1511.03276. [Google Scholar]
- Allahverdyan, A.E.; Nieuwenhuizen, T.M. Breakdown of the Landauer bound for information erasure in the quantum regime. Phys. Rev. E 2001, 64, 056117. [Google Scholar] [CrossRef] [PubMed]
- Esposito, M.; Ochoa, M.A.; Galperin, M. Nature of heat in strongly coupled open quantum systems. Phys. Rev. B 2015, 92, 235440. [Google Scholar] [CrossRef]
- Kosloff, R.; Tal-Ezer, H. A direct relaxation method for calculating eigenfunctions and eigenvalues of the Schrödinger equation on a grid. Chem. Phys. Lett. 1986, 127, 223–230. [Google Scholar] [CrossRef]
- Kosloff, R. Time-dependent quantum-mechanical methods for molecular dynamics. J. Phys. Chem. 1988, 92, 2087–2100. [Google Scholar] [CrossRef]
- Baer, R.; Kosloff, R. Quantum dissipative dynamics of adsorbates near metal surfaces: A surrogate Hamiltonian theory applied to hydrogen on nickel. J. Chem. Phys. 1997, 106, 8862–8875. [Google Scholar] [CrossRef]
- Tal-Ezer, H.; Kosloff, R. An accurate and efficient scheme for propagating the time dependent Schrödinger equation. J. Chem. Phys. 1984, 81, 3967–3971. [Google Scholar] [CrossRef]
- Bartsch, C.; Gemmer, J. Dynamical typicality of quantum expectation values. Phys. Rev. Lett. 2009, 102, 110403. [Google Scholar] [CrossRef] [PubMed]
- Cramer, M.; Eisert, J. A quantum central limit theorem for non-equilibrium systems: Exact local relaxation of correlated states. New J. Phys. 2010, 12, 055020. [Google Scholar] [CrossRef]
- Jin, F.; Steinigeweg, R.; de Raedt, H.; Michielsen, K.; Campisi, M.; Gemmer, J. Eigenstate thermalization hypothesis and quantum Jarzynski relation for Pure initial states. 2016; arXiv:1603.02833. [Google Scholar]
- Torrontegui, E.; Kosloff, R. Activated and non activated dephasing demonstrated in NV center dynamics. 2015; arXiv:1511.00981. [Google Scholar]
- Gordon, J. Generalized power vs. efficiency characteristics of heat engines: The thermoelectric generator as an instructive illustration. Am. J. Phys. 1991, 59, 551–555. [Google Scholar] [CrossRef]
- Correa, L.A.; Palao, J.P.; Alonso, D. Internal dissipation and heat leaks in quantum thermodynamic cycles. Phys. Rev. E 2015, 92, 032136. [Google Scholar] [CrossRef] [PubMed]
- Uzdin, R.; Levy, A.; Kosloff, R. Quantum equivalence and quantum signatures in heat engines. Phys. Rev. X 2015, 5, 031044. [Google Scholar]
- Uzdin, R.; Levy, A.; Kosloff, R. Quantum heat machines equivalence, work extraction beyond markovianity, and strong coupling via heat exchangers. Entropy 2016, 18, 124. [Google Scholar] [CrossRef]
- Sánchez, R.; Sothmann, B.; Jordan, A.N. Heat diode and engine based on quantum Hall edge states. New J. Phys. 2015, 17, 075006. [Google Scholar] [CrossRef]
- Sánchez, R.; Sothmann, B.; Jordan, A.N. Effect of incoherent scattering on three-terminal quantum Hall thermoelectrics. Physica E 2016, 75, 86–92. [Google Scholar] [CrossRef]
- Fornieri, A.; Blanc, C.; Bosisio, R.; D’Ambrosio, S.; Giazotto, F. Nanoscale phase engineering of thermal transport with a Josephson heat modulator. Nat. Nanotechnol. 2016, 11, 258–262. [Google Scholar] [CrossRef] [PubMed]
- Geva, E.; Kosloff, R. The quantum heat engine and heat pump: An irreversible thermodynamic analysis of the three-level amplifier. J. Chem. Phys. 1996, 104, 7681–7699. [Google Scholar] [CrossRef]
- Levy, A.; Alicki, R.; Kosloff, R. Quantum refrigerators and the third law of thermodynamics. Phys. Rev. E 2012, 85, 061126. [Google Scholar] [CrossRef] [PubMed]
- Levy, A.; Alicki, R.; Kosloff, R. Comment on “Cooling by Heating: Refrigeration Powered by Photons”. Phys. Rev. Lett. 2012, 109, 248901. [Google Scholar] [CrossRef] [PubMed]
- Gelbwaser-Klimovsky, D.; Alicki, R.; Kurizki, G. Minimal universal quantum heat machine. Phys. Rev. E 2013, 87, 012140. [Google Scholar] [CrossRef] [PubMed]
- Correa, L.A.; Mehboudi, M. Testing a quantum heat pump with a two-level spin. Entropy 2016, 18, 141. [Google Scholar] [CrossRef]










| Potential Parameters | Values | Units |
| 0.2–2 | ||
| 0 | ||
| 1.5 | ||
| A | 0.5 | |
| σ | 0.5 | |
| Grid Parameters | Typical Values | Units |
| Grid spacing, | 0.0273 | |
| Number of grid points, | 128 | |
| Time steps, | 0.12 | fsec |
| Order of Chebychev polynomials | 128 | |
| Reduced mass, μ | 1836 | |
| Hot and Cold Bath Parameters | Typical Values | Units |
| Number of bath modes (h/c) | 8 | |
| Cutoff frequency, | 2.0 | eV |
| System–bath coupling, Γ | 0.5 | |
| System–bath coupling range, γ | 0.5 | |
| Swap rate, ζ | 1.05 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katz, G.; Kosloff, R. Quantum Thermodynamics in Strong Coupling: Heat Transport and Refrigeration. Entropy 2016, 18, 186. https://doi.org/10.3390/e18050186
Katz G, Kosloff R. Quantum Thermodynamics in Strong Coupling: Heat Transport and Refrigeration. Entropy. 2016; 18(5):186. https://doi.org/10.3390/e18050186
Chicago/Turabian StyleKatz, Gil, and Ronnie Kosloff. 2016. "Quantum Thermodynamics in Strong Coupling: Heat Transport and Refrigeration" Entropy 18, no. 5: 186. https://doi.org/10.3390/e18050186
APA StyleKatz, G., & Kosloff, R. (2016). Quantum Thermodynamics in Strong Coupling: Heat Transport and Refrigeration. Entropy, 18(5), 186. https://doi.org/10.3390/e18050186