Discrete Time Dirac Quantum Walk in 3+1 Dimensions
Abstract
:1. Introduction
2. Quantum Walks
Fourier Representation of Abelian QW s
3. The Dirac QW in One, Two, and Three Space Dimensions
3.1. The Weyl Quantum Walk
3.2. The Massive Case
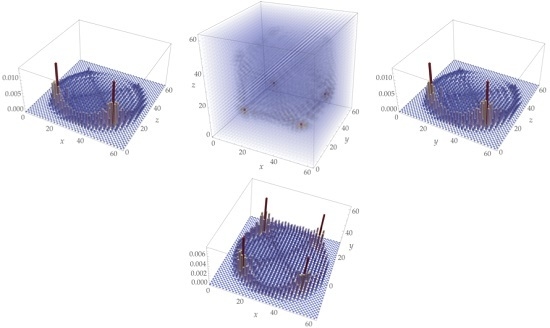
4. Numerical Simulation of the Weyl and Dirac QW s
5. Kinematics of the Dirac QW
5.1. Approximated Dispersive Differential Equation
5.2. The Evolution of the QW Position Operator
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Van Kampen, N.G. Stochastic Processes in Physics and Chemistry; Elsevier: Amsterdam, The Netherlands, 1992; Volume 1. [Google Scholar]
- Weiss, G. Aspects and Applications of the Random Walk (Random Materials & Processes S.); North-Holland: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Cox, D.R. Renewal Theory; Methuen: London, UK, 1962; Volume 1. [Google Scholar]
- Aharonov, Y.; Davidovich, L.; Zagury, N. Quantum random walks. Phys. Rev. A 1993, 48, 1687–1690. [Google Scholar] [CrossRef] [PubMed]
- Aharonov, D.; Ambainis, A.; Kempe, J.; Vazirani, U. Quantum walks on graphs. In Proceedings of the Thirty-Third Annual ACM Symposium on Theory of Computing—STOC ’01, Heraklion, Greece, 6–8 July 2001; pp. 50–59.
- Ambainis, A.; Bach, E.; Nayak, A.; Vishwanath, A.; Watrous, J. One-dimensional quantum walks. In Proceedings of the Thirty-Third Annual ACM Symposium on Theory of Computing—STOC ’01, Heraklion, Greece, 6–8 July 2001; pp. 37–49.
- Childs, A.M.; Cleve, R.; Deotto, E.; Farhi, E.; Gutmann, S.; Spielman, D.A. Exponential algorithmic speedup by a quantum walk. In Proceedings of the Thirty-Fifth ACM Symposium on Theory of Computing—STOC ’03, San Diego, CA, USA, 9–11 June 2003; p. 59.
- Ambainis, A. Quantum walk algorithm for element distinctness. SIAM J. Comput. 2007, 37, 210–239. [Google Scholar] [CrossRef]
- Magniez, F.; Santha, M.; Szegedy, M. Quantum algorithms for the triangle problem. SIAM J. Comput. 2007, 37, 413–424. [Google Scholar] [CrossRef]
- Farhi, E.; Goldstone, J.; Gutmann, S. A quantum algorithm for the Hamiltonian NAND tree. 2007. arXiv:quant-ph/0702144. [Google Scholar]
- Santha, M. Quantum walk based search algorithms. In Proceedings of the 5th International Conference Theory and Applications of Models of Computation: (TAMC 2008), Xi’an, China, 25–29 April 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 31–46. [Google Scholar]
- Portugal, R. Quantum Walks and Search Algorithms; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Wong, T.G. Grover search with lackadaisical quantum walks. J. Phys. A Math. Theor. 2015, 48, 435304. [Google Scholar] [CrossRef]
- Nayak, A.; Vishwanath, A. Quantum Walk on the Line. 2000. arXiv:quant-ph/0010117. [Google Scholar]
- Kempe, J. Quantum random walks: An introductory overview. Contemp. Phys. 2003, 44, 307–327. [Google Scholar] [CrossRef]
- Succi, S.; Benzi, R. Lattice Boltzmann equation for quantum mechanics. Phys. D Nonlinear Phenom. 1993, 69, 327–332. [Google Scholar] [CrossRef]
- Bialynicki-Birula, I. Weyl, Dirac, and Maxwell equations on a lattice as unitary cellular automata. Phys. Rev. D 1994, 49, 6920–6927. [Google Scholar] [CrossRef]
- Meyer, D.A. From quantum cellular automata to quantum lattice gases. J. Stat. Phys. 1996, 85, 551–574. [Google Scholar] [CrossRef]
- Strauch, F. Relativistic quantum walks. Phys. Rev. A 2006, 73, 054302. [Google Scholar] [CrossRef]
- Yepez, J. Quantum lattice-gas model for computational fluid dynamics. Phys. Rev. E 2001, 63, 046702. [Google Scholar] [CrossRef] [PubMed]
- D’Ariano, G.M. The quantum field as a quantum computer. Phys. Lett. A 2012, 376, 697–702. [Google Scholar] [CrossRef]
- Bisio, A.; D’Ariano, G.M.; Tosini, A. Quantum field as a quantum cellular automaton: The Dirac free evolution in one dimension. Ann. Phys. 2015, 354, 244–264. [Google Scholar] [CrossRef]
- Bisio, A.; D’Ariano, G.M.; Tosini, A. Dirac quantum cellular automaton in one dimension: Zitterbewegung and scattering from potential. Phys. Rev. A 2013, 88, 032301. [Google Scholar] [CrossRef]
- Arrighi, P.; Nesme, V.; Forets, M. The Dirac equation as a quantum walk: Higher dimensions, observational convergence. J. Phys. A Math. Theor. 2014, 47, 465302. [Google Scholar] [CrossRef]
- Arrighi, P.; Facchini, S. Decoupled quantum walks, models of the Klein-Gordon and wave equations. Europhys. Lett. 2013, 104, 60004. [Google Scholar] [CrossRef]
- Farrelly, T.C.; Short, A.J. Discrete spacetime and relativistic quantum particles. Phys. Rev. A 2014, 89, 062109. [Google Scholar] [CrossRef]
- Farrelly, T.C.; Short, A.J. Causal fermions in discrete space-time. Phys. Rev. A 2014, 89, 012302. [Google Scholar] [CrossRef]
- Katori, M.; Fujino, S.; Konno, N. Quantum walks and orbital states of a Weyl particle. Phys. Rev. A 2005, 72, 012316. [Google Scholar] [CrossRef]
- Bracken, A.J.; Ellinas, D.; Smyrnakis, I. Free-Dirac-particle evolution as a quantum random walk. Phys. Rev. A 2007, 75, 022322. [Google Scholar] [CrossRef]
- D’Ariano, G.M.; Perinotti, P. Derivation of the Dirac equation from principles of information processing. Phys. Rev. A 2014, 90, 062106. [Google Scholar] [CrossRef]
- Bisio, A.; D’Ariano, G.M.; Perinotti, P. Quantum cellular automaton theory of light. Ann. Phys. 2016, 368, 177–190. [Google Scholar] [CrossRef]
- Bibeau-Delisle, A.; Bisio, A.; D’Ariano, G.M.; Perinotti, P.; Tosini, A. Doubly special relativity from quantum cellular automata. Europhys. Lett. 2015, 109, 50003. [Google Scholar] [CrossRef]
- Bisio, A.; D’Ariano, G.M.; Perinotti, P.; Tosini, A. Weyl, Dirac and Maxwell Quantum Cellular Automata. Found. Phys. 2015, 45, 1203–1221. [Google Scholar] [CrossRef]
- Bisio, A.; D’Ariano, G.M.; Perinotti, P.; Tosini, A. Free Quantum Field Theory from Quantum Cellular Automata. Found. Phys. 2015, 45, 1137–1152. [Google Scholar] [CrossRef]
- Schrödinger, E. Über die kräftefreie Bewegung in der relativistischen Quantenmechanik; Akademie der wissenschaften in kommission bei W. de Gruyter u. Company: Berlin, Germany, 1930. (In German) [Google Scholar]
- Cannata, F.; Ferrari, L. Effects of the nonrelativistic Zitterbewegung on the electron-phonon interaction in two-band systems. Phys. Rev. B 1991, 44, 8599. [Google Scholar] [CrossRef]
- Ferrari, L.; Russo, G. Nonrelativistic zitterbewegung in two-band systems. Phys. Rev. B 1990, 42, 7454. [Google Scholar] [CrossRef]
- Cannata, F.; Ferrari, L.; Russo, G. Dirac-like behaviour of a non-relativistic tight binding Hamiltonian in one dimension. Solid State Commun. 1990, 74, 309–312. [Google Scholar] [CrossRef]
- Lurié, D.; Cremer, S. Zitterbewegung of quasiparticles in superconductors. Physica 1970, 50, 224–240. [Google Scholar] [CrossRef]
- Shen, S.Q. Spin Transverse Force on Spin Current in an Electric Field. Phys. Rev. Lett. 2005, 95, 187203. [Google Scholar] [CrossRef] [PubMed]
- Bernardes, E.; Schliemann, J.; Lee, M.; Egues, J.C.; Loss, D. Spin-Orbit Interaction in Symmetric Wells with Two Subbands. Phys. Rev. Lett. 2007, 99, 076603. [Google Scholar] [CrossRef] [PubMed]
- Lamata, L.; León, J.; Schätz, T.; Solano, E. Dirac equation and quantum relativistic effects in a single trapped ion. Phys. Rev. Lett. 2007, 98, 253005. [Google Scholar] [CrossRef] [PubMed]
- Gerritsma, R.; Kirchmair, G.; Zähringer, F.; Solano, E.; Blatt, R.; Roos, C. Quantum simulation of the Dirac equation. Nature 2010, 463, 68–71. [Google Scholar] [CrossRef] [PubMed]
- Cserti, J.; Dávid, G. Unified description of Zitterbewegung for spintronic, graphene, and superconducting systems. Phys. Rev. B 2006, 74, 172305. [Google Scholar] [CrossRef]
- Rusin, T.M.; Zawadzki, W. Transient Zitterbewegung of charge carriers in mono-and bilayer graphene, and carbon nanotubes. Phys. Rev. B 2007, 76, 195439. [Google Scholar] [CrossRef]
- Schliemann, J.; Loss, D.; Westervelt, R.M. Zitterbewegung of electronic wave packets in III-V zinc-blende semiconductor quantum wells. Phys. Rev. Lett. 2005, 94, 206801. [Google Scholar] [CrossRef] [PubMed]
- Zawadzki, W. Zitterbewegung and its effects on electrons in semiconductors. Phys. Rev. B 2005, 72, 085217. [Google Scholar] [CrossRef]
- Zawadzki, W.; Rusin, T. Nature of electron Zitterbewegung in crystalline solids. Phys. Lett. A 2010, 374, 3533–3537. [Google Scholar] [CrossRef]
- Geim, A.; Novoselov, K. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Zawadzki, W.; Rusin, T. Zitterbewegung (trembling motion) of electrons in semiconductors: A review. J. Phys. Condens. Matter 2011, 23, 143201. [Google Scholar] [CrossRef] [PubMed]
- Vaishnav, J.Y.; Clark, C.W. Observing zitterbewegung with ultracold atoms. Phys. Rev. Lett. 2008, 100, 153002. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X. Observing Zitterbewegung for Photons near the Dirac Point of a Two-Dimensional Photonic Crystal. Phys. Rev. Lett. 2008, 100, 113903. [Google Scholar] [CrossRef] [PubMed]
- Konno, N. Quantum Random Walks in One Dimension. Quantum Inf. Process. 2002, 1, 345–354. [Google Scholar] [CrossRef]
- D’Ariano, G.M.; Mosco, N.; Perinotti, P.; Tosini, A. Path-integral solution of the one-dimensional Dirac quantum cellular automaton. Phys. Lett. A 2014, 378, 3165–3168. [Google Scholar] [CrossRef]
- D’Ariano, G.M.; Mosco, N.; Perinotti, P.; Tosini, A. Discrete Feynman propagator for the Weyl quantum walk in 2 + 1 dimensions. Europhys. Lett. 2015, 109, 40012. [Google Scholar] [CrossRef]
- Cooley, J.W.; Tukey, J.W. An algorithm for the machine calculation of complex Fourier series. Math. Comput. 1965, 19, 297–301. [Google Scholar] [CrossRef]
- Alim, U.; Möller, T. A Fast Fourier Transform with Rectangular Output on the BCC and FCC Lattices. In Proceedings of the International Conference on Sampling Theory and Applications (SampTA), Marseille, France, 18–22 May 2009.
- Huang, K. On the zitterbewegung of the Dirac electron. Am. J. Phys. 1952, 20, 479–484. [Google Scholar] [CrossRef]
- Lock, J.A. The Zitterbewegung of a free localized Dirac particle. Am. J. Phys 1979, 47, 797–802. [Google Scholar] [CrossRef]
- Bisio, A.; D’Ariano, G.M.; Perinotti, P. Lorentz symmetry for 3d Quantum Cellular Automata. 2015. arXiv:1503.01017. [Google Scholar]
- Thaller, B. Visualizing the kinematics of relativistic wave packets. 2004. arXiv:quant-ph/0409079. [Google Scholar]
- Braun, J.W.; Su, Q.; Grobe, R. Numerical approach to solve the time-dependent Dirac equation. Phys. Rev. A 1999, 59, 604–612. [Google Scholar] [CrossRef]
- Mocken, G.R.; Keitel, C.H. FFT-split-operator code for solving the Dirac equation in 2+1 dimensions. Comput. Phys. Commun. 2008, 178, 868–882. [Google Scholar] [CrossRef]
- Fillion-Gourdeau, F.; Lorin, E.; Bandrauk, A.D. Numerical solution of the time-dependent Dirac equation in coordinate space without fermion-doubling. Comput. Phys. Commun. 2012, 183, 1403–1415. [Google Scholar] [CrossRef]
- Bauke, H.; Keitel, C.H. Accelerating the Fourier split operator method via graphics processing units. Comput. Phys. Commun. 2011, 182, 2454–2463. [Google Scholar] [CrossRef]






© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Ariano, G.M.; Mosco, N.; Perinotti, P.; Tosini, A. Discrete Time Dirac Quantum Walk in 3+1 Dimensions. Entropy 2016, 18, 228. https://doi.org/10.3390/e18060228
D’Ariano GM, Mosco N, Perinotti P, Tosini A. Discrete Time Dirac Quantum Walk in 3+1 Dimensions. Entropy. 2016; 18(6):228. https://doi.org/10.3390/e18060228
Chicago/Turabian StyleD’Ariano, Giacomo Mauro, Nicola Mosco, Paolo Perinotti, and Alessandro Tosini. 2016. "Discrete Time Dirac Quantum Walk in 3+1 Dimensions" Entropy 18, no. 6: 228. https://doi.org/10.3390/e18060228
APA StyleD’Ariano, G. M., Mosco, N., Perinotti, P., & Tosini, A. (2016). Discrete Time Dirac Quantum Walk in 3+1 Dimensions. Entropy, 18(6), 228. https://doi.org/10.3390/e18060228