Greedy Algorithms for Optimal Distribution Approximation

Abstract

The approximation of a discrete probability distribution $\mathbf{t}$ by an M-type distribution $\mathbf{p}$ is considered. The approximation error is measured by the informational divergence $\mathbb{D}(\mathbf{t}\parallel \mathbf{p})$, which is an appropriate measure, e.g., in the context of data compression. Properties of the optimal approximation are derived and bounds on the approximation error are presented, which are asymptotically tight. A greedy algorithm is proposed that solves this M-type approximation problem optimally. Finally, it is shown that different instantiations of this algorithm minimize the informational divergence $\mathbb{D}(\mathbf{p}\parallel \mathbf{t})$ or the variational distance ${\parallel \mathbf{p}-\mathbf{t}\parallel }_1$.

1. Introduction

In this work, we consider finite precision representations of probabilistic models. Suppose the original model, or target distribution, has n non-zero mass points and is given by $\mathbf{t}:=(t_1,\cdots ,t_n)$. We wish to approximate it by a distribution $\mathbf{p}:=(p_1,\cdots ,p_n)$ of which each entry is a rational number with a fixed denominator. In other words, for every i, $p_i=c_i/M$ for some non-negative integer $c_i\le M$. The distribution $\mathbf{p}$ is called an M-type distribution, and the positive integer $M\ge n$ is the precision of the approximation. The problem is non-trivial, since computing the numerator $c_i$ by rounding $M{t}_i$ to the nearest integer in general fails to yield a distribution.

M-type approximations have many practical applications, e.g., in political apportionments, M seats in a parliament need to be distributed to n parties according to the result of some vote $\mathbf{t}$. This problem led, e.g., to the development of multiplier methods [1]. In communications engineering, example applications are finite precision implementations of probabilistic data compression [2], distribution matching [3], and finite-precision implementations of Bayesian networks [4,5]. In all of these applications, the M-type approximation $\mathbf{p}$ should be close to the target distribution $\mathbf{t}$ in the sense of an appropriate error measure. Common choices for this approximation error are the variational distance and the informational divergences:

$$\begin{array}{}\mathrm{(1a)}& \hfill {\parallel \mathbf{p}-\mathbf{t}\parallel }_1& :=\sum _{i=1}^n|p_i-t_i|\hfill \mathrm{(1b)}& \hfill \mathbb{D}(\mathbf{p}\parallel \mathbf{t})& :=\sum _{i:p_i>0}{p}_{i}log\frac{p_i}{t_i}\hfill \mathrm{(1c)}& \hfill \mathbb{D}(\mathbf{t}\parallel \mathbf{p})& :=\sum _{i:t_i>0}{t}_{i}log\frac{t_i}{p_i}\hfill \end{array}$$

where log denotes the natural logarithm.

Variational distance and informational divergence Equation (1b) have been considered by Reznik [6] and Böcherer [7], respectively, who presented algorithms for optimal M-type approximation and developed bounds on the approximation error. In a recent manuscript [8], we extended the existing works on Equation (1a,b) to target distributions with infinite support ($n=\infty$) and refined the bounds from [6,7].

In this work, we focus on the approximation error Equation (1c). It is an appropriate cost function for data compression [9] (Theorem 5.4.3) and seems appropriate for the approximation of parameters in Bayesian networks (see Section 4). Nevertheless, to the best of the authors’ knowledge, the characterization of M-type approximations minimizing $\mathbb{D}(\mathbf{t}\parallel \mathbf{p})$ has not received much attention in literature so far.

Our contributions are as follows. In Section 2, we present an efficient greedy algorithm to find M-type distributions minimizing Equation (1c). We then discuss in Section 3 the properties of the optimal M-type approximation and bound the approximation error Equation (1c). Our bound incorporates a reverse Pinsker inequality recently suggested in [10] (Theorem 7). The algorithm we present is an instance of a greedy algorithm similar to steepest ascent hill climbing [11] (Chapter 2.6). As a byproduct, we unify this work with [6,7,8] by showing that also the algorithms optimal w.r.t. variational distance Equation (1a) and informational divergence Equation (1b) are instances of the same general greedy algorithm, see Section 2.

2. Greedy Optimization

In this section, we define a class of problems that can be optimally solved by a greedy algorithm. Consider the following example:

Example 1. 

Suppose there are n queues with jobs, and you have to select M jobs minimizing the total time spent. A greedy algorithm suggests to select successively the job with the shortest duration, among the jobs that are at the front of their queues. If the jobs in each queue are ordered by increasing duration, then this greedy algorithm is optimal.

We now make this precise: Let M be a positive integer, e.g., the number of jobs that have to be completed, and let ${\delta }_i:\mathbb{N}\to \mathbb{R}$, $i=1,\cdots ,n$, be a set of functions, e.g., ${\delta }_i\left(k\right)$ is the duration of the k-th job in the i-th queue. Let furthermore ${\mathbf{c}}_0:=(c_{1,0},\cdots ,c_{n,0})\in {\mathbb{N}}_0^n$ be a pre-allocation, representing a constraint that has to be fulfilled (e.g., in the i-th queue at least $c_{i,0}$ jobs have to be completed) or a chosen initialization. Then, the goal is to minimize

$$U\left(\mathbf{c}\right):=\sum _{i=1}^n\sum _{k_i=c_{i,0}+1}^{c_i}{\delta }_i\left(k_i\right)$$

(2)

i.e., to find a final allocation $\mathbf{c}:=(c_1,\cdots ,c_n)$ satisfying ${\parallel \mathbf{c}\parallel }_1=M$ and, for every i, $c_i\ge c_{i,0}$. A greedy method to obtain such a final allocation is presented in Algorithm 1. We show in Appendix A.1. that this algorithm is optimal if the functions ${\delta }_i$ satisfy certain conditions:

Algorithm 1: Greedy Algorithm

Initialize $k_i=c_{i,0},i=1,\cdots ,n.$

repeat $M-{\parallel {\mathbf{c}}_0\parallel }_1$ times

Compute ${\delta }_i(k_i+1),i=1,\cdots ,n.$

Compute $j=\min {\mathrm{argmin}}_i{\delta }_i(k_i+1).$ // (choose one minimal element) Update $k_j\leftarrow k_j+1,.$

end repeat

Return c = (k1, ⋯, kn).

Proposition 1. 

If the functions ${\delta }_i\left(k\right)$ are non-decreasing in k, Algorithm 1 achieves a global minimum $U\left(\mathbf{c}\right)$ for a given pre-allocation ${\mathbf{c}}_0$ and a given M.

Remark 1. 

The minimum of $U\left(\mathbf{c}\right)$ may not be unique.

Remark 2. 

If a function $f_i:\mathbb{R}\to \mathbb{R}$ is convex, the difference ${\delta }_i\left(k\right)=f_i\left(k\right)-f_i(k-1)$ is non-decreasing in k. Hence, Algorithm 1 also minimizes

$$U\left(\mathbf{c}\right)=\sum _{i=1}^n{f}_i\left(c_i\right).$$

(3)

Remark 3. 

Note that the functions ${\delta }_i\left(k\right)$ need not be non-negative, i.e., in the view of Example 1, jobs may have negative duration. The functions ${\delta }_i\left(k\right)$ are non-negative, though, if $f_i:\mathbb{R}\to \mathbb{R}$ in Remark 2 is convex and non-decreasing.

Remark 2 connects Algorithm 1 to steepest ascent hill climbing [11] (Chapter 2.6) with fixed step size and a constrained number of M steps.

We now show that instances of Algorithm 1 can find M-type approximations $\mathbf{p}$ minimizing each of the cost functions in Equation (1). Noting that $p_i=c_i/M$ for some non-negative integer $c_i$, we can rewrite the cost functions as follows:

$$\begin{array}{}\mathrm{(4a)}& \hfill {\parallel \mathbf{p}-\mathbf{t}\parallel }_1& =\hfill & \frac{1}{M}\sum _{i=1}^n|c_i-M{t}_i|\hfill \mathrm{(4b)}& \hfill \mathbb{D}(\mathbf{p}\parallel \mathbf{t})& =\hfill & \frac{1}{M}\left(\sum _{i:c_i>0}{c}_{i}log\frac{c_i}{t_i}\right)-logM\hfill \mathrm{(4c)}& \hfill \mathbb{D}(\mathbf{t}\parallel \mathbf{p})& =\hfill & logM-H\left(\mathbf{t}\right)-\sum _{i:t_i>0}{t}_{i}log{c}_i\hfill \end{array}$$

where $H(·)$ denotes entropy in nats.

Ignoring constant terms, these cost functions are all instances of Remark 2 for convex functions $f_i:\mathbb{R}\to \mathbb{R}$ (see

Table 1. Instances of Algorithm 1 Optimizing Equation (1).

Cost	$f_i\left(x\right)$	${\delta }_i\left(k\right)$	$c_{i,0}$	References
${\parallel \mathbf{p}-\mathbf{t}\parallel }_1$	$|x-M{t}_i|$	$|k-M{t}_i|-|k-1-M{t}_i|$	$\lfloor M{t}_i\rfloor$	[6,8]
$\mathbb{D}(\mathbf{p}\parallel \mathbf{t})$	$xlog(x/t_i)$	$klog\frac{k}{k-1}+log(k-1)-log{t}_i$	0	[7,8]
$\mathbb{D}(\mathbf{t}\parallel \mathbf{p})$	$-t_{i}logx$	$t_{i}log((k-1)/k)$	$\lceil t_i\rceil$	This work

). Hence, the three different M-type approximation problems set up by Equation (1) can all be solved by instances of Algorithm 1, for a trivial pre-allocation ${\mathbf{c}}_0=\mathbf{0}$ and after taking M steps. The final allocation $\mathbf{c}$ simply defines the M-type approximation by $p_i=c_i/M$.

For variational distance optimal approximation, we showed in [8] (Lemma 3), that every optimal M-type approximation satisfies $p_i\ge \lfloor M{t}_i\rfloor /M$, hence one may speed up the algorithm by pre-allocating $c_{i,0}=\lfloor M{t}_i\rfloor$. We furthermore show in Lemma 1 below that the support of the optimal M-type approximation in terms of Equation (1c) equals the support of $\mathbf{t}$ (if $M\ge n$). Assuming that $\mathbf{t}$ is positive, one can pre-allocate the algorithm with $c_{i,0}=1$. We summarize these instantiations of Algorithm 1 in Table 1.

This list of instances of Algorithm 1 minimizing information-theoretic or probabilistic cost functions can be extended. For example, the ${\chi }^2$-divergences ${\chi }^2\left(\mathbf{t}\right|\left|\mathbf{p}\right)$ and ${\chi }^2\left(\mathbf{p}\right|\left|\mathbf{t}\right)$ can also be minimized, since the functions inside the respective sums are convex. However, Rényi divergences of orders $\alpha \ne 1$ cannot be minimized by applying Algorithm 1.

3. $\mathit{M}$-Type Approximation Minimizing $\mathbb{D}(\mathbf{t}\parallel \mathbf{p})$

As shown in the previous section, Algorithm 1 presents a minimizer of the problem ${min}_{\mathbf{p}}\mathbb{D}(\mathbf{t}\parallel \mathbf{p})$ if instantiated according to Table 1. Let us call this minimizer ${\mathit{t}}^{\mathrm{a}}$. Recall that $\mathbf{t}$ is positive and that $M\ge n$. The support of ${\mathit{t}}^{\mathrm{a}}$ must contain the support of $\mathbf{t}$, since otherwise $\mathbb{D}(\mathbf{t}\parallel {\mathit{t}}^{\mathrm{a}})=\infty$. Note further that the costs ${\delta }_i\left(k\right)$ are negative if $t_i>0$ and zero if $t_i=0$; hence, if $t_i=0$, the index i cannot be chosen by Algorithm 1, thus also $t_i^{\mathrm{a}}=0$. This proves:

Lemma 1. 

If $M\ge n$, the supports of $\mathbf{t}$ and ${\mathbf{t}}^{\mathrm{a}}$ coincide, i.e., $t_i=0\iff t_i^{\mathrm{a}}=0$.

The assumption that $\mathbf{t}$ is positive and that $M\ge n$ hence comes without loss of generality. In contrast, neither variational distance nor informational divergence Equation (1b) require $M\ge n$: As we show in [8], the M-type approximation problem remains interesting even if $M<n$.

Based on Lemma 1, the following example explains why the optimal M-type approximation does not necessarily result in a “small” approximation error:

Example 2. 

Let $\mathbf{t}=(1-\epsilon ,\frac{\epsilon }{n-1},\cdots ,\frac{\epsilon }{n-1})$ and $M=n$, hence by Lemma 1, ${\mathit{t}}^{\mathrm{a}}=\frac{1}{n}(1,1,\cdots ,1)$. It follows that $\mathbb{D}(\mathbf{t}\parallel {\mathit{t}}^{\mathrm{a}})=logn-H\left(\mathbf{t}\right)$, which can be made arbitrarily close to $logn$ by choosing a small positive ε.

In Table 1 we made use of [8] (Lemma 3), which says that every $\mathbf{p}$ minimizing the variational distance ${\parallel \mathbf{p}-\mathbf{t}\parallel }_1$ satisfies $p_i\ge \lfloor M{t}_i\rfloor /M$, to speed up the corresponding instance of Algorithm 1 by proper pre-allocation. Initialization by rounding is not possible when minimizing $\mathbb{D}(\mathbf{t}\parallel \mathbf{p})$, as shown in the following two examples:

Example 3. 

Let $\mathbf{t}=(17/20,3/40,3/40)$ and $M=20$. The optimal M-type approximation is $\mathbf{p}=(8/10,1/10,1/10)$, hence $p_1<\lfloor M{t}_1\rfloor /M$. Initialization via rounding off fails.

Example 4. 

Let $\mathbf{t}=(0.719,0.145,0.088,0.048)$ and $M=50$. The optimal M-type approximation is $\mathbf{p}=(0.74,0.14,0.08,0.04)$, hence $p_1>\lceil M{t}_1\rceil /M$. Initialization via rounding up fails.

To show that informational divergence vanishes for $M\to \infty$, assume that $M>1/t_i$ for all i. Since the variational distance optimal approximation ${\mathit{t}}^{\mathrm{vd}}$ satisfies $t_i^{\mathrm{vd}}\ge \lfloor M{t}_i\rfloor /M$ for every i, ${\mathit{t}}^{\mathrm{vd}}$ has the same support as $\mathbf{t}$, which ensures that $\mathbb{D}(\mathbf{t}\parallel {\mathit{t}}^{\mathrm{vd}})<\infty$. By similar arguments as in the proof of [8] (Proposition 4), we obtain

$$\mathbb{D}(\mathbf{t}\parallel {\mathit{t}}^{\mathrm{a}})\le \mathbb{D}(\mathbf{t}\parallel {\mathit{t}}^{\mathrm{vd}})\le log\left(1+\frac{n}{2M}\right)\stackrel{M\to \infty }{⟶}0.$$

(5)

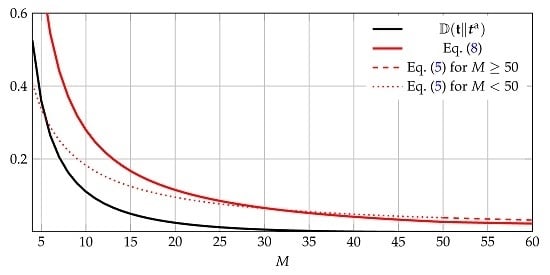
Note that this bound is universal, i.e., it prescribes the same convergence rate for every target distribution with n mass points.

We now develop an upper bound on $\mathbb{D}(\mathbf{t}\parallel {\mathit{t}}^{\mathrm{a}})$ that holds for every M. To this end, we first approximate $\mathbf{t}$ by a distribution ${\mathbf{t}}^{*}$ in ${\mathcal{P}}_M:=\{\mathbf{p}:\forall i:p_i\ge 1/{M,\parallel \mathbf{p}\parallel }_1=1\}$ that minimizes $\mathbb{D}(\mathbf{t}\parallel {\mathbf{t}}^{*})$. If ${\mathbf{t}}^{*}$ is unique, then it is called the reverse I-projection [12] (Section I.A) of $\mathbf{t}$ onto ${\mathcal{P}}_M$. Since ${\mathbf{t}}^{*}\in {\mathcal{P}}_M$, its variational distance optimal approximation ${\mathit{t}}^{\mathrm{vd}}$ has the same support as $\mathbf{t}$, which allows us to bound $\mathbb{D}(\mathbf{t}\parallel {\mathit{t}}^{\mathrm{a}})$ by $\mathbb{D}(\mathbf{t}\parallel {\mathit{t}}^{\mathrm{vd}})$.

Lemma 2. 

Let ${\mathbf{t}}^{*}\in {\mathcal{P}}_M$ minimize $\mathbb{D}(\mathbf{t}\parallel {\mathbf{t}}^{*})$. Then,

$$t_i^{*}:=\frac{t_i}{\nu \left(M\right)}+{\left(\frac{1}{M}-\frac{t_i}{\nu \left(M\right)}\right)}^{+}$$

(6)

where $\nu \left(M\right)$ is such that $\parallel {\mathbf{t}}^{*}{\parallel }_1=1$, and where ${\left(x\right)}^{+}:=max\{0,x\}$.

Proof. 

See Appendix A.2.  ☐

Let $\mathcal{K}:=\{i:t_i<\nu \left(M\right)/M\}$, $k:=\left|\mathcal{K}\right|$, and $T_{\mathcal{K}}:={\sum }_{i\in \mathcal{K}}{t}_i$. The parameter $\nu \left(M\right)$ must scale the mass $(1-T_{\mathcal{K}})$ such that it equals $(M-k)/M$, i.e., we have

$$\begin{array}{c}\hfill \nu \left(M\right)=\frac{1-T_{\mathcal{K}}}{1-\frac{k}{M}}.\end{array}$$

(7)

If, for all i, $t_i>1/M$, then $\mathbf{t}\in {\mathcal{P}}_M$, hence ${\mathbf{t}}^{*}=\mathbf{t}$ is feasible and $\nu \left(M\right)=1$. One can show that $\nu \left(M\right)$ decreases with M.

Proposition 2 

(Approximation Bounds).

$$\begin{array}{cc}\hfill \mathbb{D}(\mathbf{t}\parallel {\mathit{t}}^{\mathrm{a}})& \le log\nu \left(M\right)+\frac{log\left(2\right)}{2}\left(1-\nu \left(M\right)\left(1-\frac{n}{M}\right)\right)\hfill \end{array}$$

(8)

Proof. 

See Appendix A.3.  ☐

The first term on the right-hand side of Equation (8) accounts for the error caused by first approximating $\mathbf{t}$ by ${\mathbf{t}}^{*}$ (in the sense of Lemma 2). The second term accounts for the additional error caused by the M-type approximation of ${\mathbf{t}}^{*}$ and incorporates the reverse Pinsker inequality [10] (Theorem 7). If $M>t_i$ for every i, hence $\mathbf{t}\in {\mathcal{P}}_M$, then $\nu \left(M\right)=1$ and the bound simplifies to

$$\begin{array}{cc}\hfill \mathbb{D}(\mathbf{t}\parallel {\mathit{t}}^{\mathrm{a}})& \le log\left(2\right)\frac{n}{2M}.\hfill \end{array}$$

(9)

For M sufficiently large, Equation (8) thus yields better results than Equation (5), which approximates to $n/\left(2M\right)$. Moreover, for M sufficiently large, our bound Equation (8) is uniform, i.e., it prescribes the same convergence rate for every target distribution with n mass points. We illustrate the bounds for an example in Figure 1.

4. Applications and Outlook

Arithmetic coding uses a probabilistic model to compress a source sequence. Applying Algorithm 1 with cost Equation (1c) to the empirical distribution of the source sequence provides an M-type distribution as a probabilistic model. The parameter M can be choosen small for reduced complexity. Another application of Algorithm 1 can be found in [3], which considers the problem of generating length-M sequences according to a desired distribution. Since a length-M sequence has an M-type empirical distribution, the Reference [3] applies Algorithm 1 with cost Equation () to pre-calculate the M-type approximation of the desired distribution.

Algorithm 1 can also be used to calculate the M-type approximation of Markov models, i.e., approximating the transition matrix $\mathbf{T}$ of an n-state, irreducible Markov chain with invariant distribution vectors μ by a transition matrix $\mathbf{P}$ containing only M-type probabilities. Generalizing Equation (1c), the approximation error can be measured by the informational divergence rate [13]

$$\overline{\mathbb{D}}(\mathbf{T}\parallel \mathbf{P}):=\sum _{i,j=1}^n{\mu }_i{T}_{ij}log\frac{T_{ij}}{P_{ij}}=\sum _{i=1}^n{\mu }_i\mathbb{D}({\mathbf{t}}_i\parallel {\mathbf{p}}_i).$$

(10)

The optimal M-type approximation is found by applying the instance of Algorithm 1 to each row separately, and Lemma 1 ensures that the transition graph of $\mathbf{P}$ equals that of $\mathbf{T}$, i.e., the approximating Markov chain is irreducible. Future work shall extend this analysis to hidden Markov models and should investigate the performance of these algorithms in practical scenarios, e.g., speech processing with finite-precision arithmetic.

Another possible application is the approximation of Bayesian network parameters. The authors of [4] approximated the true parameters using a stationary multiplier method from [14]. Since rounding probabilities to zero led to bad classification performance, they replaced zeros in the approximating distribution afterwards by small values. This in turn led to the problem that probabilities that are in fact zero, were approximated by a non-zero probability. We believe that these problems can be removed by instantiating Algorithm 1 for cost Equation (1c). This automatically prevents approximating non-zero probabilities with zeros and vice-versa, see Lemma 1.

Finally, for approximating Bayesian network parameters, recent work suggests rounding log-probabilities, i.e., to approximate $log{t}_i$ by $log{p}_i=-c_i/M$ for a non-negative integer $c_i$ [5]. Finding an optimal approximation that corresponds to a true distribution is equivalent to solving

$$\begin{array}{cc}& mind(\mathbf{t},\mathbf{p})\hfill \\ & \mathrm{s}.\mathrm{t}.\parallel e^{-\mathbf{c}}{\parallel }_{1/M}=1\hfill \end{array}$$

where $d(·,·)$ denotes any of the considered cost functions Equation (1). If $M=1$ and $d(\mathbf{t},\mathbf{p})=\mathbb{D}(\mathbf{t}\parallel \mathbf{p})$ using the binary logarithm, the constraint translates to the requirement that $\mathbf{t}$ is approximated by a complete binary tree. Then, the optimal approximation is the Huffman code for $\mathbf{t}$.