A Novel Image Encryption Scheme Using the Composite Discrete Chaotic System
Abstract
:1. Introduction
2. Composite Discrete Chaotic System
2.1. Two-Dimensional Composite Discrete Chaotic System
2.2. Sensitivity Analysis of the Initial Values and Control Parameters in CDCS
- Step 1:
- Get 6 different CDCS by setting , respectively. Then, we obtain 6 chaotic sequences with the initial value by Equations (3) and (4), respectively. If the output is larger than 1, then we let in Equation (3) and in Equation (4), and if the output , then . Next, we turn them into 6 binary sequence by .
- Step 2:
- Extend the plain gray image matrix to an 1-dimensional integer sequence, and transform the integer sequence into a binary sequence.
- Step 3:
- Do exclusive OR for the binary sequence with the 6 chaotic binary sequences, respectively, then get 6 diffused binary sequences
- Step 4:
2.3. Trajectory
2.4. Gottwald and Melbourne Test
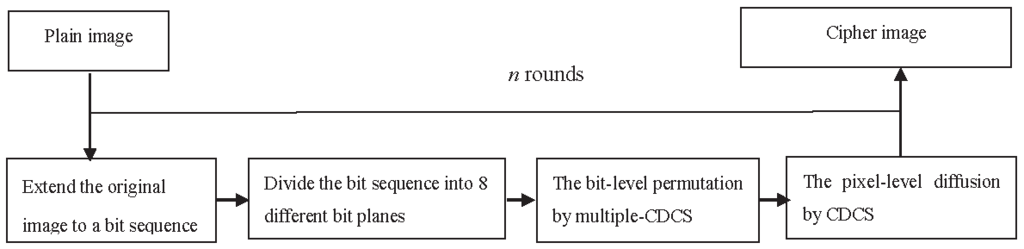
3. The Proposed Scheme
3.1. Secret Key Generation
| Algorithm 1. The generation of the secret key |
| Input: Random key K with length of 505 bits |
| Output: Secret key used in the proposed algorithm. |
| 1: ; |
| 2: for ; |
| 3: ; |
| 4: ; |
| 5: end for |
| 6: for ; |
| 7: ; |
| 8: ; |
| 9: end for |
| 10: for ; |
| 11: ; |
| 12: ; |
| 13: end for |
| 14: ; |
| 15: ; |
| 16: for |
| 17: |
| 18: end for |
| 19: for |
| 20: ; |
| 21: end for |
3.2. Encryption Process
3.2.1. Bit-Level Permutation Stage
- Step 1:
- Extend the plain image gray value matrix to a binary sequence: . Then, turn E into 8 different bit planes: by the following rules: , , , , , , , .
- Step 2:
- Step 3:
- Permutate the binary sequence by in the following way to get a shuffled binary sequence :
- Step 4:
- Rearrange the 8 permutated binary sequences into the permutated sequence J with size in the following way:
- Step 5:
- Divide the intermediate binary sequence J into blocks: , , ⋯, , then change each block into an integer, and get the permutated integer sequence , and reshape to the permutated image.
3.2.2. Pixel-Level Diffusion Stage
- Step 1:
- Step 2:
- For each , do the following operations:In Equation (11), the initial value , , where and are random value, is the i-th row and the j-th pixel of the plain image, respectively. is the final encrypted value of the k-th pixel value.
- Step 3:
- Reshape the encrypted integer sequence C back to the 2-dimensional gray value matrix of size to form the finally encrypted image.
3.3. Decryption Process
3.3.1. Pixel-Level Diffusion Decryption Stage
- Step 1:
- For the encrypted image, turn it into an integer sequence: .
- Step 2:
- Step 3:
- Let the initial value . For each , do the following operations to get the permutated sequence :Note that when , in order to get , in Equation (12), we let , , where are the same used in the encryption procedure.
3.3.2. Bit-Level Permutation Decryption Stage
- Step 1:
- Extend the decrypted sequence to a binary sequence , where is the length of , respectively. Then, turn binary sequence G into 8 different bit planes by the following rules: , , , , , , , .
- Step 2:
- Get the 8 chaotic sequences of size again by Equations (3) and (4) with the 8 pairs same parameters (, k) used in the encryption procedure, and denote them as . If the output is larger than 1, we let in Equation (3) and in Equation (4), and if the output , then . Then, sort in ascending order and get 8 index order sequences .
- Step 3:
- Permutate the binary sequence by , in the following way to obtain the original binary sequence :
- Step 4:
- Rearrange the 8 permutated binary sequences into the permutated sequence P of size in the following way: , .
- Step 5:
- Divide the intermediate binary sequence Q into blocks: , , ⋯, , then turn each block into an integer, and get the decrypted integer sequence .
- Step 6:
- Reshape the decrypted integer sequence P back to the 2-dimensional gray value matrix of size to get the finally decrypted image.
4. Simulation Results and Security Analyses
4.1. Gray and Color Image Encryption
4.2. Key Size Analysis
4.3. The Chi-Square Test Analysis of Cipher Image
4.4. Correlation Analysis
4.5. Information Entropy Analysis
4.6. Local Shannon Entropy Analysis
4.7. Key Sensitivity Analysis
4.7.1. Encrypted Key Sensitivity Analysis
- :
- A = (0.34556788,0.13456790, 0.24567981, 0.34567932, 0.42345679, 0.53456794, 0.64567958, 0.76456793, 0.86456797,0.754712846, 0.567889322), B = (π, 8, 7, 6, 5, 4, 3, 2, 13,11,10).
- :
- A = (0.34556789,0.13456790, 0.24567981, 0.34567932, 0.42345679, 0.53456794, 0.64567958, 0.76456793, 0.86456797,0.754712846, 0.567889322), B = (π, 8, 7, 6, 5, 4, 3, 2, 13,11,10).
- :
- A = (0.34556788, 0.13456791, 0.24567981, 0.34567932, 0.42345679, 0.53456794, 0.64567958, 0.76456793, 0.86456797,0.754712846, 0.567889322), B = (π, 8, 7, 6, 5, 4, 3, 2, 13,11,10).
- :
- A = (0.34556788,0.13456790, 0.24567982, 0.34567932, 0.42345679, 0.53456794, 0.64567958, 0.76456793, 0.86456797,0.754712846, 0.567889322), B = (π, 8, 7, 6, 5, 4, 3, 2, 13,11,10).
- :
- A = (0.34556788,0.13456790, 0.24567981, 0.34567931, 0.42345679, 0.53456794, 0.64567958, 0.76456793, 0.86456797,0.754712846, 0.567889322), B = (π, 8, 7, 6, 5, 4, 3, 2, 13,11,10).
- :
- A = (0.34556788,0.13456790, 0.24567981, 0.34567932, 0.42345680, 0.53456794, 0.64567958, 0.76456793, 0.86456797,0.754712846, 0.567889322), B = (π, 8, 7, 6, 5, 4, 3, 2, 13,11,10).
- :
- A = (0.34556788,0.13456790, 0.24567981, 0.34567932, 0.42345679, 0.53456795, 0.64567958, 0.76456793, 0.86456797,0.754712846, 0.567889322), B = (π, 8, 7, 6, 5, 4, 3, 2, 13,11,10).
- :
- A = (0.34556788,0.13456790, 0.24567981, 0.34567932, 0.42345679, 0.53456794, 0.64567959, 0.76456793, 0.86456797,0.754712846, 0.567889322), B = (π, 8, 7, 6, 5, 4, 3, 2, 13,11,10).
- :
- A = (0.34556788,0.13456790, 0.24567981, 0.34567932, 0.42345679, 0.53456794, 0.64567958, 0.76456794, 0.86456797,0.754712846, 0.567889322), B = (π, 8, 7, 6, 5, 4, 3, 2, 13,11,10)
- :
- A = (0.34556788,0.13456790, 0.24567981, 0.34567932, 0.42345679, 0.53456794, 0.64567958, 0.76456793, 0.86456798, 0.754712846, 0.567889322), B = (π, 8, 7, 6, 5, 4, 3, 2, 13,11,10)
- :
- A = (0.34556788,0.13456790, 0.24567981, 0.34567932, 0.42345679, 0.53456794, 0.64567958, 0.76456793, 0.86456797, 0.754712847, 0.567889322), B = (π, 8, 7, 6, 5, 4, 3, 2, 13,11,10)
- :
- A = (0.34556788,0.13456790, 0.24567981, 0.34567932, 0.42345679, 0.53456794, 0.64567958, 0.76456793, 0.86456797, 0.754712846, 0.567889323), B = (π, 8, 7, 6, 5, 4, 3, 2, 13,11,10)
4.7.2. Decrypted Key Sensitivity Analysis
4.8. Chosen/Known Plaintext Attacks Analysis
4.9. Differential Attack Analysis
4.10. Randomness Analysis of CDCS
4.11. Speed Performance
4.12. Robustness of the Proposed Algorithm in Noise and Data Loss
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fridrich, J. Symmetric ciphers based on two-dimensional chaotic maps. Int. J. Bifurc. Chaos 1998, 8, 1259–1284. [Google Scholar] [CrossRef]
- Ye, G. Image scrambling encryption algorithm of pixel bit based on chaos map. Pattern Recognit. Lett. 2014, 31, 347–354. [Google Scholar]
- Norouzi, B.; Mirzakuchaki, S. A fast color image encryption algorithm based on hyper-chaotic systems. Nonlinear Dyn. 2014, 78, 995–1015. [Google Scholar] [CrossRef]
- Baptista, M.S. Cryptography with chaos. Phys. Lett. A 1998, 240, 50–54. [Google Scholar] [CrossRef]
- Wang, X.Y.; Zhang, Y.Q.; Bao, X.M. A colour image encryption scheme using permutation-substitution based on chaos. Entropy 2015, 17, 3877–3897. [Google Scholar] [CrossRef]
- Murillo-Escobar, M.A.; Cruz-Hernandez, C.; Abundiz-Perez, F.; Lopez-Gutierrez, R.M.; del Campo, O.A. A RGB image encryption algorithm based on total plain image characteristics and chaos. Signal Process. 2015, 109, 119–131. [Google Scholar] [CrossRef]
- Zheng, Y.; Jin, J. A novel image encryption scheme based on Henon map and compound spatiotemporal chaos. Multimed. Tools Appl. 2014, 74, 7803–7820. [Google Scholar] [CrossRef]
- Zhou, Y.; Bao, L.; Philip Chen, C.L. Image encryption using a new parametric switching chaotic system. Signal Process. 2013, 93, 3039–3052. [Google Scholar] [CrossRef]
- Liu, W.; Sun, K.; Zhu, C. A fast image encryption algorithm based on chaotic map. Opt. Lasers Eng. 2016, 84, 26–36. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y.; Pun, C.-M.; Philip Chen, C.L. 2D Sine Logistic modulation map for image encryption. Inf. Sci. 2015, 297, 80–94. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y. Image encryption using 2D Logistic-adjusted-Sine map. Inf. Sci. 2016, 339, 237–253. [Google Scholar]
- Mollaeefar, M.; Sharif, A.; Nazari, M. A novel encryption scheme for colored image based on high level chaotic maps. Multimed. Tools Appl. 2015, 74, 1–23. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, H. A novel image encryption algorithm based on genetic recombination and hyper-chaotic systems. Nonlinear Dyn. 2015, 83, 333–346. [Google Scholar] [CrossRef]
- Wu, X.; Wang, D.; Kurths, J.; Kan, H. A novel lossless color image encryption scheme using 2D DWT and 6D hyperchaotic system. Inf. Sci. 2016, 349, 137–153. [Google Scholar] [CrossRef]
- Wu, X.; Bai, C.; Kan, H. A new color image cryptosystem via hyperchaos synchronization. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 1884–1897. [Google Scholar] [CrossRef]
- Zhu, H.; Zhao, C.; Zhang, X. A novel image encryption-compression scheme using hyper-chaos and Chinese remainder theorem. Signal Process. Image Commun. 2013, 28, 670–680. [Google Scholar] [CrossRef]
- Tong, X.; Wang, Z.; Liu, Y.; Zhang, M.; Xu, L. A novel compound chaotic block cipher for wireless sensor networks. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 120–133. [Google Scholar] [CrossRef]
- Wang, L.; Song, H.; Liu, P. A novel hybrid color image encryption algorithm using two complex chaotic systems. Opt. Lasers Eng. 2016, 77, 118–125. [Google Scholar] [CrossRef]
- Tong, X.; Zhang, M.; Wang, Z.; Liu, Y. An image encryption scheme based on dynamical perturbation and linear feedback shift register. Nonlinear Dyn. 2014, 78, 2277–2291. [Google Scholar] [CrossRef]
- Tong, X.; Cui, M. Image encryption scheme based on 3d baker with dynamical compound chaotic sequence cipher generator. Signal Process. 2009, 89, 480–491. [Google Scholar] [CrossRef]
- Tong, X. The novel bilateral-diffusion image encryption algorithm with dynamical compound chaos. J. Syst. Softw. 2012, 85, 850–859. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhang, W.; Wong, K.W.; Yu, H. A chaos-based symmetric image encryption scheme using a bit-level permutation. Inf. Sci. 2011, 181, 1171–1186. [Google Scholar] [CrossRef]
- Zhang, W.; Yu, H.; Zhao, Y.; Zhu, Z. Image encryption based on three-dimensional bit matrix permutation. Signal Process. 2016, 118, 36–50. [Google Scholar] [CrossRef]
- Fu, C.; Huang, J.B.; Wang, N.N.; Hou, Q.B.; Lei, W.M. A Symmetric chaos-based image cipher with an improved bit-Level permutation strategy. Entropy 2014, 16, 770–788. [Google Scholar] [CrossRef]
- Zhu, H.; Zhao, C.; Zhang, X.; Yang, L. An image encryption scheme using generalized Arnold map and affine cipher. Optik 2014, 125, 6672–6677. [Google Scholar] [CrossRef]
- Wang, X.; Luan, D. A novel image encryption algorithm using chaos and reversible cellular automata. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 3075–3085. [Google Scholar] [CrossRef]
- Song, C.; Qiao, Y. A novel image encryption algorithm based on DNA encoding and spatiotemporal chaos. Entropy 2015, 17, 6954–6968. [Google Scholar] [CrossRef]
- Wu, X.; Kan, H.; Kurths, J. A new color image encryption scheme based on DNA sequences and multiple improved 1D chaotic maps. Appl. Soft. Comput. 2015, 37, 24–39. [Google Scholar] [CrossRef]
- Ye, G. A block image encryption algorithm based on wave transmission and chaotic systems. Nonlinear Dyn. 2014, 75, 417–427. [Google Scholar] [CrossRef]
- Li, C.; Liu, Y.; Xie, T.; Chen, M. Breaking a novel image encryption scheme based on improved hyperchaotic sequences. Nonlinear Dyn. 2013, 73, 2083–2089. [Google Scholar] [CrossRef]
- Jeng, F.G.; Huang, W.L.; Chen, T.H. Cryptanalysis and improvement of two hyper-chaos-based image encryption schemes. Signal Process. Image Commun. 2015, 34, 45–51. [Google Scholar] [CrossRef]
- Li, C.; Lo, K.T. Optimal quantitative cryptanalysis of permutation-only multimedia ciphers against plaintext attacks. Signal Process. 2011, 91, 949–954. [Google Scholar] [CrossRef]
- Li, C. Cracking a hierarchical chaotic image encryption algorithm based on permutation. Signal Process. 2015, 118, 203–210. [Google Scholar] [CrossRef]
- Li, C.; Li, S.; Lo, K.T. Breaking a modified substitution-diffusion image cipher based on chaotic standard and logistic maps. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 37–843. [Google Scholar] [CrossRef] [Green Version]
- Seyedzadeh, S.M.; Mirzakuchaki, S. A fast color image encryption algorithm based on coupled two-dimensional piecewise chaotic map. Signal. Process. 2012, 92, 1202–1215. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X. Triple-image encryption scheme based on one-time key stream generated by chaos and plain images. J. Syst. Softw. 2013, 86, 826–834. [Google Scholar] [CrossRef]
- Gottwald, G.A.; Melbourne, I. A new test for chaos in deterministic systems. Proc. R. Soc. Lond. A 2004, 460, 603–611. [Google Scholar] [CrossRef]
- The USC-SIPI Image Database. Available online: http://sipi.usc.edu/database/database.php?volume=misc (accessed on 25 July 2016).
- Wu, Y.; Zhou, Y.; Saveriades, G.; Agaian, S.; Noonan, J.P.; Natarajan, P. Local Shannon entropy measure with statistical tests for image randomness. Inf. Sci. 2013, 222, 323–342. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, D. Cryptanalysis of S-box-only chaotic image ciphers against chosen plaintext attack. Nonlinear Dyn. 2013, 72, 751–756. [Google Scholar]
- A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications. Available online: http://csrc.nist.gov/publications/nistpubs/800-22-rev1a/SP800-22rev1a.pdf (accessed on 10 April 2016).











| Chaotic Sequence | x0 = 0.65382364 | x0 = 0.65382365 |
|---|---|---|
| 0.6916087935 | 0.5510774642 | |
| 0.6190457067 | 0.3196168464 | |
| 0.4879461173 | 0.3993617501 | |
| 0.8447332446 | 0.5513615043 | |
| 0.8303411884 | 0.3205043035 | |
| 0.8128237059 | 0.4008410954 | |
| 0.7909787683 | 0.5546711225 | |
| 0.7250674640 | 0.3306693894 | |
| 0.6974535701 | 0.4180539361 | |
| 0.6709209552 | 0.595164073 |
| Control Parameter | k = 2 | k = 3 | k = 4 | k = 5 | k = 6 | k = 7 |
|---|---|---|---|---|---|---|
| k = 2 | 0 | 0.99607849 | 0.99603271 | 0.99586487 | 0.99604797 | 0.99598694 |
| k = 3 | 0.99607849 | 0 | 0.99621582 | 0.99627686 | 0.99639893 | 0.9962616 |
| k = 4 | 0.99603271 | 0.99621582 | 0 | 0.99629211 | 0.99645996 | 0.9962616 |
| k = 5 | 0.99586487 | 0.99627686 | 0.99629211 | 0 | 0.99615479 | 0.99568176 |
| k = 6 | 0.99604797 | 0.99639893 | 0.99645996 | 0.99615479 | 0 | 0.99591064 |
| k = 7 | 0.99598694 | 0.9962616 | 0.9962616 | 0.99568176 | 0.99591064 | 0 |
| Initial Value x0 | Control Parameters k | Test Results |
|---|---|---|
| 0.12345678 | k = 2 | 0.99823000 |
| 0.12345679 | k = 2 | 0.99839183 |
| 0.12345677 | k = 2 | 0.99790976 |
| 0.12345676 | k = 2 | 0.99798716 |
| 0.21345678 | k= 3 | 0.99782871 |
| 0.21345678 | k = 4 | 0.99831404 |
| 0.21345678 | k = 5 | 0.99842179 |
| 0.21345678 | k = 6 | 0.99854142 |
| 0.321345678 | k = 7 | 0.99735072 |
| Image Name | p-value |
|---|---|
| 5.2.08 | 0.257198003 |
| 5.2.09 | 0.22534446 |
| 5.2.10 | 0.220229861 |
| 7.1.01 | 0.200104753 |
| 7.1.02 | 0.115958523 |
| 7.1.03 | 0.478716242 |
| 7.1.04 | 0.477272383 |
| 7.1.05 | 0.536532281 |
| 7.1.06 | 0.681580846 |
| 7.1.07 | 0.492913738 |
| 7.1.08 | 0.919338576 |
| 7.1.09 | 0.101262279 |
| boat.512 | 0.631836356 |
| elaine | 0.52057636 |
| lena | 0.224053673 |
| goldhill | 0.883876476 |
| peppers | 0.13530398 |
| baboon | 0.763747416 |
| house(R) | 0.099225363 |
| house(G) | 0.412077954 |
| house(B) | 0.285299456 |
| Test Image | Direction | Plain Image | Proposed Scheme | Ref. [16] | Ref. [22] | Ref. [8] | Ref. [25] |
|---|---|---|---|---|---|---|---|
| horizontal | 0.98727175 | 0.00911870 | −0.01598859 | 0.00921633 | −0.03444986 | 0.0255741 | |
| lena | vertical | 0.99060282 | −0.02799349 | −0.00928994 | 0.00438226 | 0.0162397 | −0.0060722 |
| diagonal | 0.98232025 | −0.008005781 | 0.00955705 | 0.00984828 | 0.05472108 | 0.03712793 | |
| horizontal | 0.98359562 | 0.00984443 | −0.01681935 | 0.02161067 | 0.04823954 | 0.00106722 | |
| goldhill | vertical | 0.97498297 | 0.01843329 | 0.03527012 | 0.03929575 | −0.01953583 | 0.01852442 |
| diagonal | 0.96849169 | 0.002687612 | 0.006798479 | 0.02047153 | −0.01473057 | 0.01321081 | |
| horizontal | 0.98486792 | 0.06072394 | 0.0237943 | 0.02161067 | −0.00350778 | −0.0115003 | |
| peppers | vertical | 0.97916019 | −0.00116499 | −0.011170982 | −0.037837 | −0.021423 | −0.00237434 |
| diagonal | 0.97515696 | −0.00571419 | 0.00664635 | 0.02047153 | 0.02345089 | −0.00098435 | |
| horizontal | 0.74954747 | −0.03856932 | −0.02999071 | 0.0161014 | 0.00289877 | −0.00547718 | |
| house(R) | vertical | 0.80262072 | 0.002023 | −0.0154941 | −0.04053886 | 0.018131106 | −0.01215746 |
| diagonal | 0.60609133 | 0.00207905 | −0.01487206 | −0.00227398 | 0.018180302 | −0.01803246 | |
| horizontal | 0.76294284 | 0.00181239 | −0.0161565 | 0.0485065 | −0.00423018 | −0.03230305 | |
| house(G) | vertical | 0.86429319 | −0.01279169 | −0.00183728 | 0.01576013 | 0.00157326 | 0.0002708 |
| diagonal | 0.66868095 | 0.00241394 | 0.00156149 | −0.03474189 | -0.003761 | −0.00867577 | |
| horizontal | 0.90852712 | −0.00921239 | 0.02068469 | 0.015610986 | −0.04302791 | 0.02820804 | |
| house(B) | vertical | 0.9477393 | 0.0034053 | −0.02170484 | −0.00567228 | 0.0137757 | 0.0107359 |
| diagonal | 0.86744223 | −0.0217718 | −0.0075945 | 0.01271975 | 0.00921989 | 0.03581673 |
| Test Image | Plain Image | The Proposed Scheme | Ref. [16] | Ref. [22] | Ref. [8] | Ref. [25] |
|---|---|---|---|---|---|---|
| 5.2.08 | 7.201008 | 7.9992989 | 7.9970096 | 7.9993075 | 7.999206 | 7.9993742 |
| 5.2.09 | 6.9939942 | 7.9992833 | 7.9968423 | 7.9992492 | 7.9991342 | 7.9992579 |
| 5.2.10 | 5.7055602 | 7.9992883 | 7.9969656 | 7.9993485 | 7.9992213 | 7.9993323 |
| 7.1.01 | 6.0274148 | 7.9993239 | 7.9972729 | 7.9993146 | 7.9991445 | 7.9993389 |
| 7.1.02 | 4.0044994 | 7.9993947 | 7.9931779 | 7.999289 | 7.9989956 | 7.9993285 |
| 7.1.03 | 5.49574 | 7.9992167 | 7.997577 | 7.9993951 | 7.9991431 | 7.9993135 |
| 7.1.04 | 6.1074181 | 7.9991862 | 7.9970146 | 7.9993017 | 7.999126 | 7.9993481 |
| 7.1.05 | 6.5631956 | 7.9992767 | 7.9969023 | 7.9993046 | 7.9991403 | 7.9993864 |
| 7.1.06 | 6.6952834 | 7.999398 | 7.9975578 | 7.999246 | 7.9992993 | 7.9992284 |
| 7.1.07 | 5.9915988 | 7.9992502 | 7.997237 | 7.9992476 | 7.9989706 | 7.9992728 |
| 7.1.08 | 5.053448 | 7.9992442 | 7.9967758 | 7.9993288 | 7.9989898 | 7.9991881 |
| 7.1.09 | 6.1898137 | 7.99938 | 7.9972559 | 7.9991956 | 7.9991552 | 7.9992166 |
| boat.512 | 7.1913702 | 7.9993893 | 7.997026 | 7.99931 | 7.9991832 | 7.9993511 |
| lena | 7.4455676 | 7.9993283 | 7.9973605 | 7.9993589 | 7.999155 | 7.9992604 |
| goldhill | 7.4777796 | 7.9993354 | 7.9974798 | 7.9992933 | 7.9992657 | 7.999319 |
| baboon | 7.3735278 | 7.9992275 | 7.9970364 | 7.9993183 | 7.9991787 | 7.9993072 |
| peppers | 7.5714776 | 7.9992535 | 7.9974015 | 7.9991921 | 7.9992645 | 7.9992152 |
| elaine | 7.4664262 | 7.9993301 | 7.9972385 | 7.9993498 | 7.9991789 | 7.9992656 |
| house(R) | 7.415627 | 7.9992942 | 7.9970608 | 7.999344 | 7.9992396 | 7.9992674 |
| house(G) | 7.2294792 | 7.9993214 | 7.9974495 | 7.9992617 | 7.9991642 | 7.9993073 |
| house(B) | 7.4353838 | 7.9992996 | 7.9973264 | 7.9992621 | 7.999225 | 7.9992576 |
| average | 6.6016959 | 7.9993039 | 7.9971971 | 7.9992913 | 7.9991954 | 7.9992817 |
| Test Image | The Proposed Scheme | Ref. [16] | Ref. [22] | Ref. [8] | Ref. [25] |
|---|---|---|---|---|---|
| 5.2.08 | 7.9028691 | 7.9055763 | 7.9053199 | 7.902356 | 7.9028432 |
| 5.2.09 | 7.9037385 | 7.9029891 | 7.900893 | 7.899853 | 7.9025761 |
| 5.2.10 | 7.9030217 | 7.9041229 | 7.9026793 | 7.902654 | 7.9016977 |
| 7.1.01 | 7.9031848 | 7.9031774 | 7.9031721 | 7.902634 | 7.9027515 |
| 7.1.02 | 7.9018403 | 7.8976268 | 7.9003936 | 7.901634 | 7.902448 |
| 7.1.03 | 7.9035924 | 7.9011942 | 7.901988 | 7.905423 | 7.9039657 |
| 7.1.04 | 7.902570 | 7.9060551 | 7.9023579 | 7.902125 | 7.9055074 |
| 7.1.05 | 7.9050477 | 7.9018336 | 7.9022384 | 7.883653 | 7.9044964 |
| 7.1.06 | 7.9025262 | 7.9058613 | 7.9008032 | 7.902356 | 7.9009599 |
| 7.1.07 | 7.9018694 | 7.9028083 | 7.9000806 | 7.902364 | 7.9044062 |
| 7.1.08 | 7.9031321 | 7.9028933 | 7.9032622 | 7.904456 | 7.9024535 |
| 7.1.09 | 7.9030009 | 7.8998789 | 7.9017465 | 7.90312 | 7.9025151 |
| boat.512 | 7.9026992 | 7.9000555 | 7.9017958 | 7.901879 | 7.9009823 |
| Elaine | 7.9009196 | 7.9006208 | 7.9046929 | 7.902989 | 7.9029109 |
| Lena | 7.903462 | 7.902938 | 7.900975 | 7.904512 | 7.904671 |
| Goldhill | 7.9025015 | 7.9009052 | 7.902251 | 7.9015092 | 7.9020145 |
| peppers | 7.9024452 | 7.9016155 | 7.9040266 | 7.9053045 | 7.9007481 |
| baboon | 7.9033626 | 7.9004801 | 7.9001366 | 7.902999 | 7.9013492 |
| house(R) | 7.9019456 | 7.9007318 | 7.9029686 | 7.9010447 | 7.905035 |
| house(G) | 7.9019228 | 7.904166 | 7.9023234 | 7.9058879 | 7.9033633 |
| house(B) | 7.9026658 | 7.9014576 | 7.8998792 | 7.1993477 | 7.9046128 |
| pass rate | 16/21 | 8/21 | 11/21 | 13/21 | 10/21 |
| 0 | 0.99617 | 0.99600 | 0.99207 | 0.98381 | 0.96877 | 0.93839 | 0.97691 | 0.97549 | 0.97625 | 0.99577 | 0.99630 | |
| 0.99617 | 0 | 0.99631 | 0.99622 | 0.99599 | 0.99621 | 0.99612 | 0.99609 | 0.99616 | 0.99599 | 0.99588 | 0.99615 | |
| 0.99600 | 0.99631 | 0 | 0.99613 | 0.99635 | 0.99619 | 0.99614 | 0.99597 | 0.99611 | 0.99609 | 0.99611 | 0.99604 | |
| 0.99207 | 0.99622 | 0.99613 | 0 | 0.99246 | 0.99254 | 0.99178 | 0.99192 | 0.99210 | 0.99217 | 0.99598 | 0.99597 | |
| 0.98381 | 0.99599 | 0.99635 | 0.99246 | 0 | 0.98441 | 0.98413 | 0.98443 | 0.98447 | 0.98463 | 0.99611 | 0.99612 | |
| 0.96877 | 0.99621 | 0.99619 | 0.99254 | 0.98441 | 0 | 0.96814 | 0.96885 | 0.96847 | 0.96888 | 0.99614 | 0.99615 | |
| 0.93839 | 0.99612 | 0.99614 | 0.99178 | 0.98413 | 0.96814 | 0 | 0.93682 | 0.93850 | 0.93759 | 0.99593 | 0.99614 | |
| 0.97691 | 0.99609 | 0.99597 | 0.99192 | 0.98443 | 0.96885 | 0.93682 | 0 | 0.95173 | 0.90193 | 0.99608 | 0.99616 | |
| 0.97549 | 0.99616 | 0.99611 | 0.99210 | 0.98447 | 0.96847 | 0.93850 | 0.95173 | 0 | 0.95015 | 0.99604 | 0.99623 | |
| 0.97625 | 0.99599 | 0.99609 | 0.99217 | 0.98463 | 0.96888 | 0.93759 | 0.90193 | 0.95015 | 0 | 0.99617 | 0.99622 | |
| 0.99577 | 0.99588 | 0.99611 | 0.99598 | 0.99611 | 0.99614 | 0.99593 | 0.99608 | 0.99604 | 0.99617 | 0 | 0.99606 | |
| 0.99630 | 0.99615 | 0.99604 | 0.99597 | 0.99612 | 0.99615 | 0.99614 | 0.99616 | 0.99623 | 0.99622 | 0.99606 | 0 |
| Round | The Proposed Scheme | Ref. [16] | Ref. [22] | Ref. [8] | Ref. [25] |
|---|---|---|---|---|---|
| 1 | 0.6696014404 | 0.000015259 | 0.00654386 | 0.9960098267 | 0.9963431625 |
| 2 | 0.995967865 | 0.000015259 | 0.80495842 | 0.9960746765 | 0.9959527564 |
| 3 | 0.9961090088 | 0.000015259 | 0.99615466 | 0.9961242676 | 0.9965357538 |
| 4 | 0.9961585999 | 0.000015259 | 0.99595247 | 0.9961776733 | 0.9960346326 |
| 5 | 0.9961013794 | 0.000015259 | 0.99616793 | 0.9959716797 | 0.9961644326 |
| Round | The Proposed Scheme | Ref. [16] | Ref. [22] | Ref. [8] | Ref. [25] |
|---|---|---|---|---|---|
| 1 | 0.2630562577 | 0.000012087 | 0.00321365 | 0.3326689627 | 0.3360676146 |
| 2 | 0.3353189655 | 0.000012087 | 0.24366436 | 0.3348488303 | 0.335123463 |
| 3 | 0.3346790837 | 0.000012087 | 0.33401162 | 0.3351597805 | 0.3350163487 |
| 4 | 0.3342736338 | 0.000012087 | 0.33389708 | 0.3346462175 | 0.3344254165 |
| 5 | 0.3340085647 | 0.000012087 | 0.33441636 | 0.3348087535 | 0.3343425278 |
| Test Name | p-value | Results |
|---|---|---|
| Frequency test | 0.5731 | Success |
| Block Frequency test | 0.6825 | Success |
| Cusum-Forward test | 0.9293 | Success |
| Cusum-Reverse test | 0.3514 | Success |
| Runs test | 0.5536 | Success |
| Long Runs test of Ones | 0.6154 | Success |
| Binary Matrix Rank Test | 0.7635 | Success |
| Spectral DFT test | 0.4674 | Success |
| Non-overlapping test Templates (m = 9, B = 000000001) | 0.8710 | Success |
| Overlapping test Templates (m = 9) | 0.9241 | Success |
| Maurer’s Universal test (L = 7, Q = 1280) | 0.3533 | Success |
| Approximate Entropy test (m = 5) | 0.9987 | Success |
| Random Excursions test (x = +1) | 0.2085 | Success |
| Lempel Ziv compression test | 0.6784 | Success |
| Linear complexity test | 0.2314 | Success |
| Random Excursions Variant test (x = −1) | 0.5811 | Success |
| Serial test (m = 5,) | 0.8989 | Success |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.; Zhang, X.; Yu, H.; Zhao, C.; Zhu, Z. A Novel Image Encryption Scheme Using the Composite Discrete Chaotic System. Entropy 2016, 18, 276. https://doi.org/10.3390/e18080276
Zhu H, Zhang X, Yu H, Zhao C, Zhu Z. A Novel Image Encryption Scheme Using the Composite Discrete Chaotic System. Entropy. 2016; 18(8):276. https://doi.org/10.3390/e18080276
Chicago/Turabian StyleZhu, Hegui, Xiangde Zhang, Hai Yu, Cheng Zhao, and Zhiliang Zhu. 2016. "A Novel Image Encryption Scheme Using the Composite Discrete Chaotic System" Entropy 18, no. 8: 276. https://doi.org/10.3390/e18080276
APA StyleZhu, H., Zhang, X., Yu, H., Zhao, C., & Zhu, Z. (2016). A Novel Image Encryption Scheme Using the Composite Discrete Chaotic System. Entropy, 18(8), 276. https://doi.org/10.3390/e18080276