Next Article in Journal
Acoustic Detection of Coronary Occlusions before and after Stent Placement Using an Electronic Stethoscope
Previous Article in Journal
Entropy Generation through Non-Equilibrium Ordered Structures in Corner Flows with Sidewall Mass Injection
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Entropy
Volume 18
Issue 8
10.3390/e18080280
entropy-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Acoustic Entropy of the Materials in the Course of Degradation

by
Ali Kahirdeh
† and
M. M. Khonsari
*
Department of Mechanical Engineering, Louisiana State University, Baton Rouge, LA 70803, USA
*
Author to whom correspondence should be addressed.
†
Current address: Department of Engineering, Central Connecticut State University, New Britain, CT 06050, USA
Entropy 2016, 18(8), 280; https://doi.org/10.3390/e18080280
Submission received: 1 July 2016 / Revised: 21 July 2016 / Accepted: 25 July 2016 / Published: 28 July 2016
Browse Figures
Versions Notes

Abstract

:
We report experimental observations on the evolution of acoustic entropy in the course of cyclic loading as degradation occurs due to fatigue. The measured entropy is a result of the materials’ microstructural changes that occur as degradation due to cyclic mechanical loading. Experimental results demonstrate that maximum acoustic entropy emanating from materials during the course of degradation remains similar. Experiments are shown for two different types of materials: Aluminum 6061 (a metallic alloy) and glass/epoxy (a composite laminate). The evolution of the acoustic entropy demonstrates a persistent trend over the course of degradation.

Graphical Abstract

1. Introduction

Materials subjected to cyclic loading undergo gradual degradation that ages the component and results in fatigue damage and eventual failure. Much progress has been made on the development of methodologies for predicting the number of cycles to failure [1,2] as well as the theoretical modeling of damage in materials [3]. Yet, to date, a reliable procedure for assessment of the degradation and cumulative damage remains elusive. To assess the material’s structural integrity, a crucial step is to first identify features in the system’s response that can properly measure the level of degradation. This aim cannot be accomplished successfully without an appropriate identification of the damage mechanisms involved. One measure of damage is disorder in the material’s microstructure. In metallic alloys, disorder is in the form of dislocation movements, slip formation, void nucleation, and growth as well as their combination. Of course, it can also be any other material’s defect induced during the manufacturing process. Non-conservative frictional sources also contribute to degradation of the material as a physical system. In the case of composite materials, the involved mechanisms are, interlayer friction between the components of the laminate, matrix cracking, debonding, delamination, and fiber breakage. Such damage mechanisms interact and coexist in the course of the loading cycles.
The initiation, formation and the propagation of damage contribute to the dissipation of the energy [4] and change in the entropy [5,6,7]. Energy is dissipated in the forms of hysteresis energy [8,9,10,11,12,13], thermal energy [14,15,16,17,18,19,20], and acoustic emissions (AE) [4,21,22,23,24,25]. In the case of dissipated thermal energy, infrared technology enables one to monitor the temperature evolution over the life of the components. Particularly in, low- to moderate-cycle fatigue where the heat liberated due to plastic deformation can be easily measured.
Entropy has been studied in several studies related to material science and degradation. Of the early studies related to entropy, production in the course of deformation of solids is due to the work the Nobel laureate Percy Bridgman [26] in which he examined the thermodynamics of plastic deformation. Related to fatigue and fracture, Whaley et al. [27,28] reported a hypothesis that the total accumulated entropy is a constant value at the time of the failure. In the context of damage mechanics, Basaran and Yan [29] interpreted the entropy as disorder and employed Boltzmann entropy to quantify the disorder in the material. The extension of their approach to electrical and chemical properties is also published in [30,31,32]. Naderi et al. [33] also reported experimental results on the existence of a entropic limit at the time of the fatigue failure.
Acoustic emissions are strain waves generated due to such microstructural changes and can be measured using piezoelectric acoustic sensors. Such waves, as direct reflections of the microstructural changes, contain information on degradation. Therefore, by extracting features from the measured signals (waveforms), it is possible to monitor the cumulative trend of degradation. Such an approach has been employed for qualitative damage assessment of a wide range of materials [22,24,25,34].
The acoustic emissions features depend on many factors such as the boundary conditions of experiment, specimens’ geometry as well as the heat treatment and microstructure of sample materials. In addition, location of the sensors and the proximity to source locations can also affect the values of the features of the acoustic emissions.
The induced microstructural-level disorder in materials can be traced in the variations of generated acoustic emissions [35]. Such variations affect the probability distribution of waveforms and their extracted features and can be quantified by information entropy.
After the seminal paper of Claude Shannon [36], information entropy has found numerous applications in a variety of disciplines such as image and signal processing by Coifman [37], Kapur et al. [38], and Sabuncu [39], vibration signal processing by Elforjani [40], flow-controlled systems by Niven [41], and protein sequences by Strait [42]. Relative entropy has been also employed by Guan [43] for crack prognostics.
Information entropy is often used for determining the order (as opposed to scatteredness) of the time-series (time-series is defined as a time-oriented sequence of data-points of a random variable being studied) [44] associated with physical measurements—a signal or an image—to quantify their information content. Information entropy [45,46] can also be interpreted as an uncertainty in a random variable, as a measure of gaining information about a random variable or as a measure of dispersion in a probability distribution of a random variable [39,45,46].
The premise of this research is that fatigue degradation and damage is a form of disorder that manifests itself in the deteriorations in the features of the acoustic emission signals, and can be quantified by employing the information entropy. Accordingly, we employ the information entropy as a distributional feature that depends on the probability distribution of the measurements, rather than each specific value. The acoustic entropy is a fraction of the total entropy generated due to the dissipative mechanisms involved in degradation.
The outline of this paper is as follows. The description of entropy estimation from acoustic response of the tested materials is discussed in Section 2. Section 3 presents the experimental results on estimation of entropy followed by conclusions in Section 4.

2. Information Entropy Estimation of Acoustic Emissions

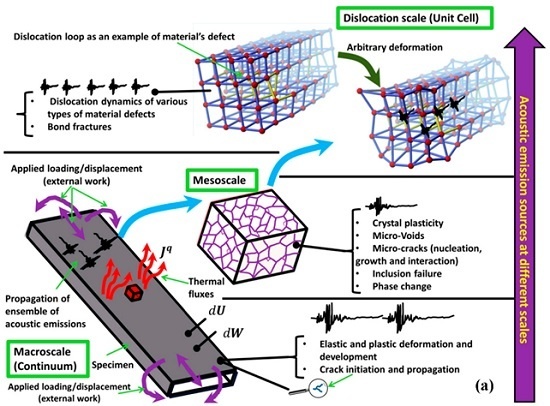
2.1. Acoustic Emission Sources in Metals and Composites

A material subjected to cyclic deformation generates strain wave that can be detected via an acoustic emission (AE) sensor. In metals, AE originates from sources within a broad range of resolution, e.g., dislocation dynamics and their formed patterns ( o ( 10 − 8 – 10 − 7 ) ) , crystal plasticity at grains ( o ( 10 − 3 ) ) and continuum plasticity at macro-scale ( o ( 10 − 3 – 10 − 2 ) ). Therefore, acoustic emission exists across several length scales.
Figure 1 depicts the sources of acoustic emission for a typical metallic material. The lower left side of the Figure 1 depicts the material at specimen size that can be considered as macroscale or continuum level. Elastic and plastic deformation, crack initiation, and propagation at this scale are the sources of acoustic emissions. An ensemble of acoustic emission waveforms propagated along the specimen can be captured employing sensors. Figure 1 also shows possible AE sources at mesoscale, such as crystal plasticity, micro-voids, micro-crack nucleation and propagation, failure of the inclusions and precipitations at boundaries, as well as phase change. At a smaller scale such as dislocation scale, sources of acoustic emissions are due to material’s defect and bond fracture. Such waveforms are emitted as the unit cell of the material undergoes any arbitrary deformations. For composite materials, the sources of emissions emerge from matrix cracking, fiber breakage, and delamination as depicted in Figure 1b.
Figure 2 shows a typical acoustic emission signal. Various features must be calculated from the measured signals. The trend of evolution of features of the signals reveals the initiation and development of the microstructural changes and damage mechanisms involved in the degradation of the material during the course of fatigue. One of the acoustic emission features is “counts” defined as the number of times that a signal exceeds a preset threshold during a fatigue test. Thus, the AE counts can be considered as a measure of intensity of the emission source.

2.2. Entropy of the Acoustic Response

The main step in estimation of the information entropy is to define the probability distribution of the random variable. We define our random variable as acoustic emission counts, n i , at each time instant where i represents the time instant that the signal is received. Assume a physical system, a specimen made of a specific material, is composed of a set of finite states ϕ 1 ,     ϕ 2 ,   … ,     ϕ i with the probability of each state designated as p i . We define integrity (degradation level) of the specimen as a macro-state directly dependent on the microstructural changes (microstates) of our physical system. At each instant of deformation/loading or any particular instant in the course of applying the input work procedure on the material, these micro- and macro-states change as our physical system—the specimen—occupies a new configuration. Let P ( p i ) represent the probability distribution of the system. The information entropy, S —often referred to as Shannon’s entropy in recognition of Claude Shannon’s classical work published in 1948—of such a distribution is defined in Equation (1) [36].
S E = ∑ i = 1 n p i log 2 ( 1 p i ) = − ∑ i = 1 n p i log 2 ( p i )
We define the set of the probabilities, { p i } , at each instant of deformation cycle as following. At each time instant as we proceed during an experiment, we define our set of data as all of the measured counts of the acoustic emissions, c i , from the initial moment of the test, t = 0 , until the current time instant, t i . Therefore, for each instant within the interval of [ 0 ,   t i ] a probability is estimated, and as the experiment continues we update this probability once new counts are received. The absolute values of the variable c i are designated by n i , where i is the time instant at which a signal is received. The probability p i is defined as the counts measured from the beginning of the test, c i = { n 0 , n 1 , … ,   n i } , divided by the total number of counts received until the current time, c i total = ∑ 0 i c i = n 0 + n 1 + … + n i . The definition of the set of { p i } at each instant of the experiment is shown below:
t i = t 0 ,     c i = { n 0 } ,     p i = { n 0 n 0 } = 1
t i = t 1 ,   c i = { n 0 ,   n 1 } ,     p i = { n 0 n 0 + n 1 , n 1 n 0 + n 1 }   and   ∑ i = 0 1 p i = 1
t i = t f ,   c i = { n 0 ,   n 1 ,   … ,   n f } ,   p i = { n 0 n 0 + n 1 + … + n f , n 1 n 0 + n 1 + … + n f , … ,   n f n 0 + n 1 + … + n f }   and   ∑ i = 0 f p i = 1
The above definition of the { p i } at each instant of the experiment satisfies the condition of ∑ 0 i p i = 1 throughout the observations from an experiment. The probabilities are updated as a new signal is received by the sensor over the course of the degradation. Once the probability distribution is obtained, information entropy is estimated using Equation (1) at each time-instant corresponding to a different configuration of the cyclically deformed material. It should be noted that the above definition of probability is a type of “experimental probability”. The definition of probability used in describing the acoustic event occurrence can be explained by a simple example of rolling a fair, six-sided dice. Once the dice is rolled the probabilities of d i = { 1 , 2 , 3 , 4 , 5 , 6 } are all equal to p i = { 1 6 , 1 6 , 1 6 , 1 6 , 1 6 , 1 6 } . However, if the observer does not know the true probability of the outcomes—e.g., if the dice is not fair or the center of mass and the center of gravity of the dice is not the same—then, according to his/her state of knowledge, the experimenter sees the problem as a “black box” problem. Thus, the only way of determining the probabilities is to repeat the rolling of the dice, observe the outcomes and calculate the probabilities based on the observed outcomes. In this way, at each rolling time, the probabilities can be updated. While the former assumes the probability of getting each side is a priori known, the latter uses an experimental approach to determine the probability of each side. Our approach is of experimental nature wherein we update the probability at each instant of the time the sensor receives a new acoustic event.
We report the experimental observations of the estimated information entropy from AE signals for two different materials in the course of the cyclic fatigue loading. The tested materials are glass/epoxy—an unbalanced woven composite—and Aluminum 6061, a metallic alloy. The fatigue experiments are fully reversed in bending mode and during experiments, the acoustic emissions are measured from samples. Additional details are available in Appendix regarding the material and specimen specifications, the test rig, the details of the acoustic emission measurement apparatus, as well as the measurement procedure.

3. Information Entropy Results

Figure 3 shows the information entropy associated with acoustic emissions counts measured during eight fully-reversed bending fatigue experiments with Aluminum 6061 specimens. Experiments were performed at a series of displacement amplitudes, each resulting in a different number of cycles to failure. Since the operational variables of the experiments—i.e., the displacement amplitude and the number of cycles to failure for all of the tests—are different, the information entropy of all of the tests cannot be demonstrated in a single graph. Therefore, to proceed, we choose the standardized form of the data where the mean value is removed from and the resultant is divided by the standard deviation of each set of data for each experiments. This representation of a data set is also known as standard score or Z-score scale. In a standardized plot, the negative values indicate that the data are smaller than the mean of the data and the positive values represent data that are larger than the mean of the data. The data in Figure 3a is then normalized with respect to the largest standardized value attained in each experiment to vary in the interval of [0, 1]. As the displacement amplitude in the fatigue test is decreased, the number of cycles to failure increases due to the decrease in plastic deformation in material. In general, tests with a longer duration (high number of cycles to fatigue) have a higher level of information entropy. However, according to the results of Figure 3a,c, a very important observation is that the trend of evolution of entropy over the course of fatigue degradation remains similar regardless of operating conditions. This behavior is easily detectable from the evolution trend of entropy in both standardized and normalized forms.
Similar results are obtained by repeating the experiments with a different material such as glass/epoxy composite. Twenty three fully-reversed bending fatigue experiments are performed on glass/epoxy samples with various displacement amplitudes in the range of 35.56 mm to 44.45mm at a frequency of 10 Hz. Some of the tests are randomly repeated to observe the typical scatteredness (fluctuations) in the fatigue life of the similar samples with a similar experimental variable  and labeled as T1, T2, etc. representing the Test number 1, 2 and so on. During an experimental study, the investigator must ascertain that operating and environmental conditions as well as boundary conditions remain similar for each set of tests. Also, specimens must be manufactured using the same manufacturing process and samples should be made from the same batch of material. Nevertheless, specimens’ microstructures are not necessarily identical and, as a result, the evolution of fatigue and degradation for each sample is different. Therefore, a scatter in the number of cycles to failure and associated entropy is an inherent feature of fatigue experiments. Repeatable evolution trend of entropy over the course of fatigue degradation is also observed over the degradation of the composite specimens. The entropy evolution is demonstrated in standardized form in Figure 4a. Similar trend of evolution is observed in Figure 4a but due to inhomogeneity in the degradation evolution in composites and its multi-step trend, variations are observed in the entropy trend. Degradation in composites is a multistep procedure [21] and involves several damage mechanisms. However, the persistent trend of evolution of acoustic entropy manifests itself in the normalized depiction of the data as seen in Figure 4c. The trend of the data is similar to those obtained for Aluminum 6061 (Figure 3c).
Figure 5 and Figure 6 depict the maximum information entropy obtained in the course of cyclic bending fatigue degradation for aluminum and glass/epoxy samples, respectively. The data points in these two graphs are the maximum values observed in the Figure 3b and Figure 4b, respectively. The examination of the results reveals that under the conditions tested the maximum measured entropy lies within a narrow band (for the range of the band refer to the box and whisker plot of the Figure 5b and Figure 6b). In Figure 5b and Figure 6b, non-parametric probability density function (PDF) of the maximum information entropy as well as box-whisker plot of the variation of the entropy are presented. This is performed to obtain a statistical inference on the distribution of the maximum information entropy. The PDF of a random variable represents the relative likelihood of data to assume a given range. The non-parametric PDFs of the maximum information entropy are obtained without assuming any prior distributions in the dataset. The central red marks represent median, and margins of the box show the 25th and 75th percentiles. Each side of the whiskers corresponds to the largest data points that are not evaluated as outliers. The median of maximum information entropy of the acoustic emissions attains a value of 13.1 bits for the experiments performed on the aluminum samples and 12.45 bits for that of performed on glass/epoxy specimens. This hints of a possible existence of an information entropic limit to the acoustic entropy generated in the course of the fatigue failure of the materials. Previously, research by Naderi et al. [33] showed that there exists a critical limit in the cumulative thermodynamic entropy generation (known as fatigue fracture entropy) beyond which fracture occurs. The evolutionary trend of the acoustic entropy, under various operating conditions tested in this study, also reveals a persistent trend over the course of the fatigue degradation.

4. Discussion and Concluding Remarks

During a cyclic fatigue test, the material tends to degrade and the formation of the damage modes is reflected in its mechanical parameters. These deteriorations in the material properties are all consequences of the same failure mechanisms—i.e., the formation and evolution of damage modes—which will result in similar trends in various responses of the material to cyclic stress such as thermal and acoustic response.
One of the materials’ responses that carry information of the microstructural changes in the material is acoustic response. In this research, we examined how information entropy of acoustic emissions can reveal pertinent information about material degradation during cyclic fatigue. We showed that regardless of the type of the material (i.e., either a metallic alloy or a composite) and displacement amplitude, the evolution of entropy of the acoustic emissions exhibits a persistent trend of evolution in the course of the fatigue degradation. Such similarities of the trend of evolution are observable in the standardized and normalized acoustic entropy.
Aside from the similarities observed in the evolution trend, it is observed that the maximum accumulated entropy of the acoustic emissions attain similar values within an error band. Specifically, under the conditions tested, it is observed that Aluminum 6061, the median value of the measured entropy is 13.1 bits and for the tests performed on glass/epoxy the median value of the measured entropy is 12.45 bits. The entropy feature has the advantage that it is defined based on the distribution of the AE feature and not solely based on the values of the measurements.
We close our discussion by emphasizing the significance of the feature selection algorithm for damage detection methodologies. The crucial step is to extract information related to the damage from the sensor outputs. Operational and environmental factors along with material properties and size scales are all determining factors that affect the sensor outputs. The effect of such factors becomes more pronounced once a more sensitive monitoring method, e.g., acoustic emission, is deployed. Features that quantify the deteriorations in probability distribution of the measurements could provide valuable information pertaining to the damage. Acoustic entropy is a fraction of the total entropy generated in the course of the degradation of a cyclically loaded solid material. This fraction of the total entropy is measureable from the material by means of AE sensors.

Author Contributions

Ali Kahirdeh and M. M. Khonsari conceived the research and designed the experiments; Ali Kahirdeh performed the experiments, data analysis, and prepared the first draft of the report. Both authors have contributed to the writing of the manuscript. Both authors have read and approved the final manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix. Materials, Experimental Apparatus, and Procedure

Fully reversed bending mode experiments are employed for calculation of the information entropy of the acoustic emissions. Two different sample materials are tested in this mode are glass/epoxy and Aluminum 6061. These different materials are selected to ascertain that the procedure is applicable broad range of applications including mechanical component, structures, and aerospace structural components. The material tested is manufactured according to the standard ASTM STP 566 [47] for use in reverse-bending fatigue tests depicted in Figure A1. All of the dimensions are in millimeters. The type of composites used in this work is glass/epoxy (G10/FR4)—an unbalanced woven fabric with plain weave-and-aligned configuration stacked in 15 layers within the thickness of 3 mm. The specimens are prepared with on-axis stacking sequences, and manufactured for use in reverse-bending fatigue tests as shown in Figure A1. The laminates are clamped at one end and the other end is oscillated with a specified amplitude and frequency. The schematic of the fatigue experimental apparatus utilized in this research is demonstrated in Figure A1. The fatigue machine is made of a bench-mounted unit containing a variable speed motor and a variable throw crank. The crank is attached to the reciprocating platen with a failure cut-off circuit in a control box and a cycle counter. The crank is adjusted from 0 to 50 mm to apply bending displacement.
A PCI-2 (Peripheral Component Interconnect)—a two-channel AE system which samples up to a rate of 10 MHz—is utilized to measure the acoustic emissions from the specimen during the entire test. A wide-band acoustic emission sensor measures the emitted waves and converts them to an electrical signal. The AE sensor is 19.02 mm in diameter and has a frequency range of 100–900 kHz. A gel-type ultrasonic couplant is used to acoustically couple the sensor to the specimen. The sensor is firmly connected to the specimen during the fatigue tests. A preamplifier is connected to the PCI-2 data acquisition system [48] using a BNC (Bayonet Neill–Concelman) cable. The preamplifier provides a 20/40/60 dB gain options that operates with either a single-ended or differential sensor. A pre-amplification of 40 dB is applied to the received signals and the plug-in filter is a band-pass with the range of 20 to 1200 kHz. The Peak Definition Time (PDT), Hit Definition Time (HDT), and Hit Lockout Time (HLT) are set to 50, 200, and 300, respectively for the fatigue experiments performed on aluminum samples and set to 50, 200, and 300, respectively. The results of the experiments performed on this test setup are shown in Figure 3, Figure 4, Figure 5 and Figure 6.
Entropy 18 00280 g007a 1024Entropy 18 00280 g007b 1024
Figure A1. Schematic diagram of the bending experimental setup employed for measurement of the acoustic emissions in the course of bending fatigue degradation. (a) The specimen diagram; (b) The experimental setup. Information entropy of the acoustic emissions is then estimated from signals measured from these experiments.
Figure A1. Schematic diagram of the bending experimental setup employed for measurement of the acoustic emissions in the course of bending fatigue degradation. (a) The specimen diagram; (b) The experimental setup. Information entropy of the acoustic emissions is then estimated from signals measured from these experiments.
Entropy 18 00280 g007aEntropy 18 00280 g007b

References

  1. Moura, A.; Lei, X.; Nishisawa, O. Prediction scheme for the catastrophic failure of highly loaded brittle materials or rocks. J. Mech. Phys. Solids 2005, 53, 2435–2455. [Google Scholar] [CrossRef]
  2. Moura, A.; Lei, X.; Nishisawa, O. Self-similarity in rock cracking and related complex critical exponents. J. Mech. Phys. Solids 2006, 54, 2544–2553. [Google Scholar] [CrossRef]
  3. Maire, J.F.; Chaboche, J.L. A new formulation of continuum damage mechanics (CDM) for composite materials. Aerosp. Sci. Technol. 1997, 1, 247–257. [Google Scholar] [CrossRef]
  4. Kahirdeh, A.; Khonsari, M.M. Energy dissipation in the course of the fatigue degradation: Mathematical derivation and experimental quantification. Int. J. Solids Struct. 2015, 77, 74–85. [Google Scholar] [CrossRef]
  5. Bryant, M.D.; Khonsari, M.M.; Ling, F.F. On the Thermodynamics of Degradation. Proc. R. Soc. Lond. A 2008, 2096. [Google Scholar] [CrossRef]
  6. Basaran, C.; Nie, S. An irreversible thermodynamics theory for damage mechanics of solids. Int. J. Damage Mech. 2004, 13, 205–223. [Google Scholar] [CrossRef]
  7. Temfack, T.; Basaran, C. Experimental verification of thermodynamic fatigue life prediction model using entropy as damage metric. Mater. Sci. Technol. 2015, 31, 1627–1632. [Google Scholar] [CrossRef]
  8. Letcher, T.; Shen, M.H.H.; Scott-Emuakpor, O.; George, T.; Cross, C. An energy-based critical fatigue life prediction method for AL6061-T6. Fatigue Fract. Eng. Mater. Struct. 2012, 35, 861–870. [Google Scholar] [CrossRef]
  9. Scott-Emuakpor, O.; George, T.; Cross, C.; Shen, M.-H.H. Hysteresis-loop representation for strain energy calculation and fatigue assessment. J. Strain Anal. Eng. Design 2010, 45, 275–282. [Google Scholar] [CrossRef]
  10. Ozaltun, H.; Shen, M.H.H.; George, T.; Cross, C. An energy based fatigue life prediction framework for in-service structural components. Exp. Mech. 2011, 51, 707–718. [Google Scholar] [CrossRef]
  11. Liakat, M.; Khonsari, M.M. Entropic characterization of metal fatigue with stress concentration. Int. J. Fatigue 2015, 70, 223–234. [Google Scholar] [CrossRef]
  12. Imanian, A.; Modarres, M. A thermodynamic entropy approach to reliability assessment with applications to corrosion fatigue. Entropy 2015, 17, 6995–7020. [Google Scholar] [CrossRef]
  13. Ontiveros, V.L.; Modarres, M.; Amiri, M. Estimation of reliability of structures subject to fatigue loading using plastic strain energy and thermodynamic entropy generation. Proc. Inst. Mech. Eng. Part O 2015, 229, 220–236. [Google Scholar] [CrossRef]
  14. Toubal, L.; Karama, M.; Lorrain, B. Damage evolution and infrared thermography in woven composite laminates under fatigue loading. Int. J. Fatigue 2006, 28, 1867–1872. [Google Scholar] [CrossRef]
  15. Naderi, M.; Kahirdeh, A.; Khonsari, M.M. Dissipated thermal energy and damage evolution of glass/epoxy using infrared thermography and acoustic emission. Compos. Part B 2012, 43, 1613–1620. [Google Scholar] [CrossRef]
  16. Meneghetti, G.; Quaresimin, M. Fatigue strength assessment of a short fiber composite based on the specific heat dissipation. Compos. Part B 2011, 42, 217–225. [Google Scholar] [CrossRef]
  17. Meneghetti, G.; Ricotta, M. The use of the specific heat loss to analyse the low- and high-cycle fatigue behaviour of plain and notched specimens made of a stainless steel. Eng. Fract. Mech. 2012, 81, 2–16. [Google Scholar] [CrossRef]
  18. Katunin, A. Thermal fatigue of polymeric composites under repeated loading. J. Reinf. Plast. Compos. 2012, 31, 1037–1044. [Google Scholar] [CrossRef]
  19. Katunin, A.; Fidali, M. Self-heating of polymeric laminated composite plates under the resonant vibrations: Theoretical and experimental study. Polym. Compos. 2012, 33, 138–146. [Google Scholar] [CrossRef]
  20. Reis, P.B.; Ferreira, J.M.; Richardson, M.W. Fatigue damage characterization by ndt in polypropylene/glass fibre composites. Appl. Compos. Mater. 2011, 18, 409–419. [Google Scholar] [CrossRef]
  21. Kahirdeh, A.; Khonsari, M.M. Criticality of degradation in composite materials subjected to cyclic loading. Compos. Part B 2014, 61, 375–382. [Google Scholar] [CrossRef]
  22. Farhidzadeh, A.; Mpalaskas, A.C.; Matikas, T.E.; Farhidzadeh, H.; Aggelis, D.G. Fracture mode identification in cementitious materials using supervised pattern recognition of acoustic emission features. Construct. Build. Mater. 2014, 67, 129–138. [Google Scholar] [CrossRef]
  23. Silva, J.M.A.; Devezas, T.C.; Silva, A.P.; Ferreira, J.A.M. Mechanical characterization of composites with embedded optical fibers. J. Compos. Mater. 2005, 39, 1261–1281. [Google Scholar] [CrossRef]
  24. Bravo, A.; Toubal, L.; Koffi, D.; Erchiqui, F. Development of novel green and biocomposite materials: Tensile and flexural properties and damage analysis using acoustic emission. Mater. Design 2015, 66, 16–28. [Google Scholar] [CrossRef]
  25. Kordatos, E.Z.; Aggelis, D.G.; Matikas, T.E. Monitoring mechanical damage in structural materials using complimentary nde techniques based on thermography and acoustic emission. Compos. Part B 2012, 43, 2676–2686. [Google Scholar] [CrossRef]
  26. Bridgman, P.W. The thermodynamics of plastic deformation and generalized entropy. Rev. Mod. Phys. 1950, 22, 56–63. [Google Scholar] [CrossRef]
  27. Whaley, P.W.; Chen, P.S.; Smith, G.M. Continuous measurement of material damping during fatigue tests. Exp. Mech. 1984, 24, 342–348. [Google Scholar] [CrossRef]
  28. Whaley, P.W. A mathematical model for internal friction and local fatigue damage based on populations of yielding microelements. J. Vib. Acoust. Stress Reliabil. Design 1987, 109, 201–206. [Google Scholar] [CrossRef]
  29. Basaran, C.; Yan, C.Y. A thermodynamic framework for damage mechanics of solder joints. J. Electron. Packag. 1998, 120, 379–384. [Google Scholar] [CrossRef]
  30. Basaran, C.; Tang, H. Implementation of a thermodynamic framework for damage mechanics of solder interconnects in microelectronics packaging. Int. J. Damage Mech. 2002, 11, 87–108. [Google Scholar] [CrossRef]
  31. Basaran, C.; Lin, M.; Ye, H. A thermodynamic model for electrical current induced damage. Int. J. Solids Struct. 2003, 40, 7315–7327. [Google Scholar] [CrossRef]
  32. Gunel, E.M.; Basaran, C. Damage characterization in non-isothermal stretching of acrylics. Part II: Experimental validation. Mech. Mater. 2011, 43, 992–1012. [Google Scholar] [CrossRef]
  33. Naderi, M.; Amiri, M.; Khonsari, M.M. On the thermodynamic entropy of fatigue fracture. Proc. R. Soc. Lond. A 2010, 466, 423–438. [Google Scholar] [CrossRef]
  34. Kakakasery, J.; Arumugam, V.; Abdul Rauf, K.; Bull, D.; Chambers, A.R.; Scarponi, C.; Santulli, C. Cure cycle effect on impact resistance under elevated temperatures in carbon prepreg laminates investigated using acoustic emission. Compos. Part B 2015, 75, 298–306. [Google Scholar] [CrossRef]
  35. Hoffmann, M.J.; Hammer, M.; Endriss, A.; Lupascu, D.C. Correlation between microstructure, strain behavior, and acoustic emission of soft pzt ceramics. Acta Mater. 2001, 49, 1301–1310. [Google Scholar] [CrossRef]
  36. Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
  37. Coifman, R.R.; Wickerhauser, M.V. Entropy-based algorithms for best basis selection. IEEE Trans. Inf. Theory 1992, 38, 713–718. [Google Scholar] [CrossRef]
  38. Kapur, J.N.; Sahoo, P.K.; Wong, A.K.C. A new method for gray-level picture thresholding using the entropy of the histogram. Comput. Vis. Graph. Image Process. 1985, 29, 273–285. [Google Scholar] [CrossRef]
  39. Sabuncu, M.R. Entropy-Based Image Registration. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 2004. [Google Scholar]
  40. Elforjani, M.; Mba, D. Accelerated natural fault diagnosis in slow speed bearings with acoustic emission. Eng. Fract. Mech. 2010, 77, 112–127. [Google Scholar] [CrossRef]
  41. Niven, R.K. Steady state of a dissipative flow-controlled system and the maximum entropy production principle. Phys. Rev. E 2009, 80, 021113. [Google Scholar] [CrossRef] [PubMed]
  42. Strait, B.J.; Dewey, T.G. The shannon information entropy of protein sequences. Biophys. J. 1996, 71, 148–155. [Google Scholar] [CrossRef]
  43. Guan, X.; Giffin, A.; Jha, R.; Liu, Y. Maximum relative entropy-based probabilistic inference in fatigue crack damage prognostics. Probabil. Eng. Mech. 2012, 29, 157–166. [Google Scholar] [CrossRef]
  44. Montgomery, D.C.; Jennings, C.L.; Kulahci, M. Introduction to Time Series Analysis and Forecasting; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
  45. Sethna, J. Statistical Mechanics: Entropy, Order Parameters and Complexity; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
  46. Caticha, A. Lectures on Probability, Entropy, and Statistical Physics. In Proceedings of the 28th International Workshop on Bayesian Inference and Maximum Entropy Methods in Science and Engineering, Sao Paulo, Brazil, 8–13 July 2008.
  47. Swanson, S.R. Handbook Of Fatigue Testing, STP566-EB. Available online: http://dx.doi.org/10.1520/STP566-EB (accessed on 27 July 2016).
  48. PCI-2—PCI-Based Two-Channel AE Board & System. Available online: http://www.physicalacoustics.com/by-product/pci-2/ (accessed on 27 July 2016).
Entropy 18 00280 g001 1024
Figure 1. Illustration of acoustic emission sources at different scales. (a) Metallic specimen; (b) Composite specimen.
Figure 1. Illustration of acoustic emission sources at different scales. (a) Metallic specimen; (b) Composite specimen.
Entropy 18 00280 g001
Entropy 18 00280 g002 1024
Figure 2. A typical acoustic emission signal with illustration of AE counts and the threshold level.
Figure 2. A typical acoustic emission signal with illustration of AE counts and the threshold level.
Entropy 18 00280 g002
Entropy 18 00280 g003 1024
Figure 3. (a) The standardized information entropy of the acoustic emission signals vs. standardized time related to the eight experiments performed on aluminum samples. The standardized time and standardized information entropy is negative for data points smaller than the mean of the data. The standardized entropy and time is obtained according to the relation z = x − μ σ where x is the variable to be standardized, μ is the mean of the data, and σ is the standard deviation of the data; (b) The variation in the standardized acoustic emission entropy in the boxplot form; (c) The normalized acoustic emission entropy with respect to the normalized time. The standardized acoustic emissions entropy is normalized with respect to the largest value obtained in the experiment.
Figure 3. (a) The standardized information entropy of the acoustic emission signals vs. standardized time related to the eight experiments performed on aluminum samples. The standardized time and standardized information entropy is negative for data points smaller than the mean of the data. The standardized entropy and time is obtained according to the relation z = x − μ σ where x is the variable to be standardized, μ is the mean of the data, and σ is the standard deviation of the data; (b) The variation in the standardized acoustic emission entropy in the boxplot form; (c) The normalized acoustic emission entropy with respect to the normalized time. The standardized acoustic emissions entropy is normalized with respect to the largest value obtained in the experiment.
Entropy 18 00280 g003
Entropy 18 00280 g004 1024
Figure 4. (a) The standardized information entropy of the acoustic emission signals vs. standardized time related to the twenty-three experiments performed on the glass/epoxy laminates. The standardized time and standardized information entropy is negative for data points smaller than the mean of the data. The standardized entropy and time is obtained according to the relation z = x − μ σ where x is the variable to be standardized, μ is the mean of the data, and σ is the standard deviation of the data; (b) The variation in the standardized acoustic emission entropy in the boxplot form; (c) The normalized acoustic emission entropy with respect to the normalized time. The standardized acoustic emissions entropy is normalized with respect to the largest value obtained in the experiment.
Figure 4. (a) The standardized information entropy of the acoustic emission signals vs. standardized time related to the twenty-three experiments performed on the glass/epoxy laminates. The standardized time and standardized information entropy is negative for data points smaller than the mean of the data. The standardized entropy and time is obtained according to the relation z = x − μ σ where x is the variable to be standardized, μ is the mean of the data, and σ is the standard deviation of the data; (b) The variation in the standardized acoustic emission entropy in the boxplot form; (c) The normalized acoustic emission entropy with respect to the normalized time. The standardized acoustic emissions entropy is normalized with respect to the largest value obtained in the experiment.
Entropy 18 00280 g004
Entropy 18 00280 g005 1024
Figure 5. (a) Maximum information entropy for eight experiments performed with Aluminum 6061 specimens in fully-reversed bending mode. The maximum information entropy in the course of the fatigue degradation obtains a median value of approximately 13.1; (b) The figure shows the non-parametric probability distribution of the maximum information entropy values as well as a box-whisker plot representing the variation in the values of the maximum information entropy. The central red marks represent median, the margins of the box show the 25th and 75th percentiles. Each side of the whiskers corresponds to the largest data points that are not evaluated as outliers.
Figure 5. (a) Maximum information entropy for eight experiments performed with Aluminum 6061 specimens in fully-reversed bending mode. The maximum information entropy in the course of the fatigue degradation obtains a median value of approximately 13.1; (b) The figure shows the non-parametric probability distribution of the maximum information entropy values as well as a box-whisker plot representing the variation in the values of the maximum information entropy. The central red marks represent median, the margins of the box show the 25th and 75th percentiles. Each side of the whiskers corresponds to the largest data points that are not evaluated as outliers.
Entropy 18 00280 g005
Entropy 18 00280 g006a 1024Entropy 18 00280 g006b 1024
Figure 6. (a) Maximum information entropy for 23 experiments performed on the glass/epoxy laminates in the fully reversed bending mode. The maximum information entropy in the course of the fatigue degradation obtains a median value of approximately 12.45; (b) The figure shows the non-parametric probability distribution of the maximum information entropy values as well as a box-whisker plot representing the variation in the values of the maximum information entropy. The central red marks represent median, the margins of the box show the 25th and 75th percentiles. Each side of the whiskers corresponds to the largest data points that are not evaluated as outliers.
Figure 6. (a) Maximum information entropy for 23 experiments performed on the glass/epoxy laminates in the fully reversed bending mode. The maximum information entropy in the course of the fatigue degradation obtains a median value of approximately 12.45; (b) The figure shows the non-parametric probability distribution of the maximum information entropy values as well as a box-whisker plot representing the variation in the values of the maximum information entropy. The central red marks represent median, the margins of the box show the 25th and 75th percentiles. Each side of the whiskers corresponds to the largest data points that are not evaluated as outliers.
Entropy 18 00280 g006aEntropy 18 00280 g006b

Share and Cite

MDPI and ACS Style

Kahirdeh, A.; Khonsari, M.M. Acoustic Entropy of the Materials in the Course of Degradation. Entropy 2016, 18, 280. https://doi.org/10.3390/e18080280

AMA Style

Kahirdeh A, Khonsari MM. Acoustic Entropy of the Materials in the Course of Degradation. Entropy. 2016; 18(8):280. https://doi.org/10.3390/e18080280

Chicago/Turabian Style

Kahirdeh, Ali, and M. M. Khonsari. 2016. "Acoustic Entropy of the Materials in the Course of Degradation" Entropy 18, no. 8: 280. https://doi.org/10.3390/e18080280

APA Style

Kahirdeh, A., & Khonsari, M. M. (2016). Acoustic Entropy of the Materials in the Course of Degradation. Entropy, 18(8), 280. https://doi.org/10.3390/e18080280

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop