Modeling Multi-Event Non-Point Source Pollution in a Data-Scarce Catchment Using ANN and Entropy Analysis
Abstract
:1. Introduction
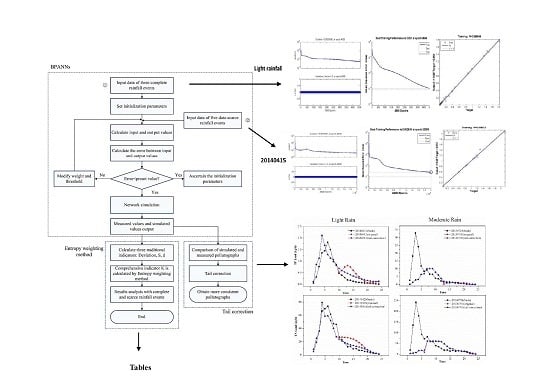
2. Materials and Methods
2.1. The Description of the ANN
2.2. The Description of the Entropy Weighting Method
2.3. Method for Tail Correction
3. Case Study
3.1. Study Areas
3.2. Field Monitoring and Data Record
4. Results and Discussion
4.1. Training Results of the ANNUsing the Complete Data
4.2. Simulated Results of the ANN for Data-Scarce Events
4.3. Implication for NPS Studies of Multi-Events
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ongley, E.D.; Zhang, X.L.; Yu, T. Current status of agricultural and rural non-point source Pollution assessment in China. Environ. Pollut. 2010, 158, 1159–1168. [Google Scholar] [CrossRef] [PubMed]
- Li, X.F.; Xiang, S.Y.; Zhu, P.F.; Wu, M. Establishing a dynamic self-adaptation learning algorithm of the BP neural network and its applications. Int. J. Bifurc. Chaos 2015, 25, 1540030. [Google Scholar] [CrossRef]
- Gong, Y.W.; Liang, X.Y.; Li, X.N.; Li, J.Q.; Fang, X.; Song, R.N. Influence of rainfall characteristics on total suspended solids in urban runoff: A case study in Beijing, China. Water 2016, 8, 278. [Google Scholar] [CrossRef]
- Coulliette, A.D.; Noble, R.T. Impacts of rainfall on the water quality of the Newport River Estuary (Eastern North Carolina, USA). J. Water Health 2008, 6, 473–482. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.L.; Gao, M.; Xie, D.T.; Ni, J.P. Spatial and temporal variations in non-point source losses of nitrogen and phosphorus in a small agricultural catchment in the Three Gorges Region. Environ. Monit. Assess. 2016, 188, 257. [Google Scholar] [CrossRef] [PubMed]
- Sajikumar, N.; Thandaveswara, B.S. A non-linear rainfall-runoff model using an artificial neural network. J. Hydrol. 1999, 216, 32–55. [Google Scholar] [CrossRef]
- Bulygina, N.; McIntyre, N.; Wheater, H. Conditioning rainfall-runoff model parameters for ungauged catchments and land management impacts analysis. Hydrol. Earth Syst. Sci. 2009, 13, 893–904. [Google Scholar] [CrossRef]
- Maniquiz, M.C.; Lee, S.; Kim, L.H. Multiple linear regression models of urban runoff pollutant load and event mean concentration considering rainfall variables. J. Environ. Sci. 2010, 22, 946–952. [Google Scholar] [CrossRef]
- Chen, N.W.; Hong, H.S.; Cao, W.Z.; Zhang, Y.Z.; Zeng, Y.; Wang, W.P. Assessment of management practices in a small agricultural watershed in Southeast China. J. Environ. Sci. Health Part A Toxic Hazard. Subst. Environ. Eng. 2006, 41, 1257–1269. [Google Scholar] [CrossRef] [PubMed]
- Sun, A.Y.; Miranda, R.M.; Xu, X. Development of multi-meta models to support surface water quality management and decision making. Environ. Earth Sci. 2015, 73, 423–434. [Google Scholar] [CrossRef]
- Yuceil, K.; Baloch, M.A.; Gonenc, E.; Tanik, A. Development of a model support system for watershed modeling: A case study from Turkey. CLEANSoil Air Water 2007, 35, 638–644. [Google Scholar] [CrossRef]
- Shope, C.L.; Maharjan, G.R.; Tenhunen, J.; Seo, B.; Kim, K.; Riley, J.; Arnhold, S.; Koellner, T.; Ok, Y.S.; Peiffer, S.; et al. Using the SWAT model to improve process descriptions and define hydrologic partitioning in South Korea. Hydrol. Earth Syst. Sci. 2014, 18, 539–557. [Google Scholar] [CrossRef]
- Jeong, J.; Kannan, N.; Arnold, J.; Glick, R.; Gosselink, L.; Srinivasan, R. Development and integration of sub-hourly rainfall-runoff modeling capability within a watershed model. Water Resour. Manag. 2010, 24, 4505–4527. [Google Scholar] [CrossRef]
- Park, Y.S.; Engel, B.A. Identifying the correlation between water quality data and LOADEST model behavior in annual sediment load estimations. Water 2016, 8, 368. [Google Scholar] [CrossRef]
- Park, Y.S.; Engel, B.A.; Frankenberger, J.; Hwang, H. A web-based tool to estimate pollutant loading using LOADEST. Water 2015, 7, 4858–4868. [Google Scholar] [CrossRef]
- Das, S.K.; Ng, A.W.M.; Perera, B.J.C.; Adhikary, S.K. Effects of climate and landuse activities on water quality in the Yarra River catchment. In Proceedings of the 20th International Congress on Modelling and Simulation (Modsim2013), Adelaide, Australia, 1–6 December 2013; pp. 2618–2624. [Google Scholar]
- Chen, D.J.; Hu, M.P.; Guo, Y.; Dahlgren, R.A. Reconstructing historical changes in phosphorus inputs to rivers from point and nonpoint sources in a rapidly developing watershed in eastern China, 1980–2010. Sci. Total Environ. 2015, 533, 196–204. [Google Scholar] [CrossRef] [PubMed]
- Melesse, A.M.; Ahmad, S.; Mcclain, M.E.; Wang, X.; Lim, Y.H. Suspended sediment load prediction of river systems: An artificial neural network approach. Agric. Water Manag. 2011, 98, 855–866. [Google Scholar] [CrossRef]
- Tran, H.D.; Muttil, N.; Perera, B.J.C. Investigation of artificial neural network models for streamflow forecasting. In Proceedings of the 19th International Congress on Modelling and Simulation (Modsim 2011), Perth, Australia, 12–16 December 2011; pp. 1099–1105. [Google Scholar]
- Hassan, M.; Shamim, M.A.; Sikandar, A.; Mehmood, I.; Ahmed, I.; Ashiq, S.Z.; Khitab, A. Development of sediment load estimation models by using artificial neural networking techniques. Environ. Monit. Assess. 2015, 187, 686. [Google Scholar] [CrossRef] [PubMed]
- Dhiman, N.; Markandeya; Singh, A.; Verma, N.K.; Ajaria, N.; Patnaik, S. Statistical optimization and artificial neural network modeling for acridine orange dye degradation using in-situ synthesized polymer capped ZnO nanoparticles. J. Colloid Interface Sci. 2017, 493, 295–306. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.W.; Ai, Z.W.; Cao, Y. Information-entropy based load balancing in parallel adaptive volume rendring. In Proceedings of the International Conferences on Interfaces and Human Computer Interaction 2015, Game and Entertainment Technologies 2015, and Computer Graphics, Visualization, Computer Vision and Image Processing 2015, Las Palmas de Gran Canaria, Spain, 22–24 July 2015; pp. 163–169. [Google Scholar]
- Khosravi, K.; Pourghasemi, H.R.; Chapi, K.; Bahri, M. Flash flood susceptibility analysis and its mapping using different bivariate models in Iran: A comparison between Shannon's entropy, statistical index, and weighting factor models. Environ. Monit. Assess. 2016, 188, 656. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.M.; Wei, G.A. Empirical studies of unblocked index for urban freeway traffic flow states. In Proceedings of the 2009 12th International IEEE Conference on Intelligent Transportation Systems, St. Louis, MO, USA, 4–7 Octorber 2009; pp. 1–6. [Google Scholar]
- Kan, J.M.; Liu, J.H. Self-Tuning PID controller based on improved BP neural network. In Proceedings of the 2009 Second International Conference on Intelligent Computation Technology and Automation, Changsha, China, 10–11 Octorber 2009; pp. 95–98. [Google Scholar]
- Chen, X.Y.; Chau, K.W. A hybrid double feedforward neural network for suspended sediment load estimation. Water Resour. Manag. 2016, 30, 2179–2194. [Google Scholar] [CrossRef]
- Guo, Z.H.; Wu, J.; Lu, H.Y.; Wang, J.Z. A case study on a hybrid wind speed forecasting method using BP neural network. Knowl. Based Syst. 2011, 24, 1048–1056. [Google Scholar] [CrossRef]
- Ju, Q.; Yu, Z.B.; Hao, Z.C.; Ou, G.X.; Zhao, J.; Liu, D.D. Division-based rainfall-runoff simulations with BP neural networks and Xinanjiang model. Neurocomputing 2009, 72, 2873–2883. [Google Scholar] [CrossRef]
- Jing, J.T.; Feng, P.F.; Wei, S.L.; Zhao, H. Investigation on surface morphology model of Si3N4 ceramics for rotary ultrasonic grinding machining based on the neural network. Appl. Surf. Sci. 2017, 396, 85–94. [Google Scholar] [CrossRef]
- Ullrich, A.; Volk, M. Influence of different nitrate-N monitoring strategies on load estimation as a base for model calibration and evaluation. Environ. Monit. Assess. 2010, 171, 513–527. [Google Scholar] [CrossRef] [PubMed]
- Wilson, D.R.; Apreleva, M.V.; Eichler, M.J.; Harrold, F.R. Accuracy and repeatability of a pressure measurement system in the patellofemoral joint. J. Biomech. 2003, 36, 1909–1915. [Google Scholar] [CrossRef]
- Ai, Y.T.; Guan, J.Y.; Fei, C.W.; Tian, J.; Zhang, F.L. Fusion information entropy method of rolling bearing fault diagnosis based on n-dimensional characteristic parameter distance. Mech. Syst. Signal Process. 2017, 88, 123–136. [Google Scholar] [CrossRef]
- Liu, F.; Zhao, S.; Weng, M.; Liu, Y. Fire risk assessment for large-scale commercial buildings based on structure entropy weight method. Saf. Sci. 2017, 94, 26–40. [Google Scholar] [CrossRef]
- Sun, L.Y.; Miao, C.L.; Yang, L. Ecological-economic efficiency evaluation of green technology innovation in strategic emerging industries based on entropy weighted TOPSIS method. Ecol. Indic. 2017, 73, 554–558. [Google Scholar] [CrossRef]
- Huang, Z.Y. Evaluating intelligent residential communities using multi-strategic weighting method in China. Energy Build. 2014, 69, 144–153. [Google Scholar] [CrossRef]
- Shen, Z.Y.; Gong, Y.W.; Li, Y.H.; Liu, R.M. Analysis and modeling of soil conservation measures in the Three Gorges Reservoir Area in China. Catena 2010, 81, 104–112. [Google Scholar] [CrossRef]
- Shen, Z.Y.; Gong, Y.W.; Li, Y.H.; Hong, Q.; Xu, L.; Liu, R.M. A comparison of WEPP and SWAT for modeling soil erosion of the Zhangjiachong Watershed in the Three Gorges Reservoir Area. Agric. Water Manag. 2009, 96, 1435–1442. [Google Scholar] [CrossRef]
- Shen, Z.; Qiu, J.; Hong, Q.; Chen, L. Simulation of spatial and temporal distributions of non-point source pollution load in the Three Gorges Reservoir Region. Sci. Total Environ. 2014, 493, 138–146. [Google Scholar] [CrossRef] [PubMed]
- Gottschalk, L.; Weingartner, R. Distribution of peak flow derived from a distribution of rainfall volume and runoff coefficient, and a unit hydrograph. J. Hydrol. 1998, 208, 148–162. [Google Scholar] [CrossRef]
- Xu, Y.F.; Ma, C.Z.; Liu, Q.; Xi, B.D.; Qian, G.R.; Zhang, D.Y.; Huo, S.L. Method to predict key factors affecting lake eutrophication—A new approach based on Support Vector Regression model. Int. Biodeterior. Biodegrad. 2015, 102, 308–315. [Google Scholar] [CrossRef]
- Wagner, P.D.; Fiener, P.; Wilken, F.; Kumar, S.; Schneider, K. Comparison and evaluation of spatial interpolation schemes for daily rainfall in data scarce regions. J. Hydrol. 2012, 464–465, 388–400. [Google Scholar] [CrossRef]
- Croke, B.; Islam, A.; Ghosh, J.; Khan, M.A. Evaluation of approaches for estimation of rainfall and the unit hydrograph. Hydrol. Res. 2011, 42, 372–385. [Google Scholar] [CrossRef]
- Ryu, J.; Jang, W.S.; Kim, J.; Jung, Y.; Engel, B.A.; Lim, K.J. Development of field pollutant load estimation module and linkage of QUAL2E with watershed-scale L-THIA ACN model. Water 2016, 8, 292. [Google Scholar] [CrossRef]
- Li, P.Y.; Qian, H.; Wu, J.H. Groundwater quality assessment based on improved water quality index in Pengyang County, Ningxia, Northwest China. J. Chem. 2010, 7, S209–S216. [Google Scholar]







| 21 April 2014 | 24 July 2014 | 5 August 2014 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Time | Flow (m3/s) | NPS-TN (mg/L) | NPS-TP (mg/L) | Time | Flow (m3/s) | NPS-TN (mg/L) | NPS-TP (mg/L) | Time | Flow (m3/s) | NPS-TN (mg/L) | NPS-TP (mg/L) |
| 2:45 | 0.002 | 4.75 | 0.063 | 22:45 | 0.003 | 0.84 | 0.11 | 21:30 | 0.008 | 2.66 | 0.30 |
| 3:00 | 0.009 | 8.89 | 0.193 | 23:00 | 0.380 | 6.26 | 0.76 | 21:45 | 0.678 | 7.29 | 0.84 |
| 3:15 | 0.015 | 15.29 | 0.300 | 23:15 | 0.647 | 6.96 | 1.04 | 22:00 | 1.107 | 11.30 | 1.12 |
| 3:30 | 0.016 | 13.31 | 0.301 | 23:30 | 0.726 | 7.06 | 0.87 | 22:15 | 1.400 | 11.90 | 1.26 |
| 3:45 | 0.031 | 25.28 | 0.369 | 23:45 | 0.336 | 6.77 | 0.92 | 22:30 | 2.227 | 9.85 | 0.94 |
| 4:00 | 0.037 | 14.14 | 0.297 | 0:00 | 0.971 | 8.77 | 1.12 | 23:00 | 1.647 | 15.00 | 1.20 |
| 4:30 | 0.065 | 22.64 | 0.652 | 0:30 | 0.570 | 8.08 | 0.70 | 23:30 | 0.585 | 9.67 | 0.62 |
| 5:00 | 0.071 | 24.48 | 0.441 | 1:00 | 0.294 | 5.53 | 0.48 | 0:00 | 0.945 | 9.56 | 0.68 |
| 6:00 | 0.086 | 26.49 | 0.469 | 2:00 | 0.266 | 5.05 | 0.57 | 1:00 | 0.410 | 7.01 | 0.35 |
| 7:00 | 0.126 | 23.89 | 0.443 | 3:00 | 0.172 | 5.11 | 0.36 | 2:00 | 0.237 | 2.03 | 0.28 |
| 8:00 | 0.146 | 16.97 | 0.286 | 4:00 | 0.191 | 5.79 | 0.34 | 3:00 | 0.183 | 7.60 | 0.37 |
| 9:00 | 0.264 | 11.60 | 0.171 | 5:00 | 0.041 | 5.85 | 0.20 | 4:00 | 0.166 | 6.81 | 0.27 |
| 10:00 | 0.278 | 11.00 | 0.117 | 6:00 | 0.090 | 5.59 | 0.18 | 5:00 | 0.115 | 7.01 | 0.20 |
| 11:00 | 0.288 | 10.73 | 0.104 | 7:00 | 0.064 | 7.78 | 0.15 | 6:00 | 0.126 | 6.71 | 0.19 |
| 12:00 | 0.296 | 10.94 | 0.109 | 8:00 | 0.048 | 5.29 | 0.14 | 7:00 | 0.102 | 6.08 | 0.12 |
| 13:00 | 0.411 | 9.64 | 0.113 | 8:00 | 0.073 | 7.03 | 0.24 | ||||
| 14:00 | 0.593 | 9.48 | 0.089 | 9:00 | 0.063 | 5.68 | 0.11 | ||||
| 15:00 | 0.593 | 9.65 | 0.087 | 10:00 | 0.086 | 5.75 | 0.09 | ||||
| 16:00 | 0.602 | 9.26 | 0.072 | 11:00 | 0.075 | 6.44 | 0.18 | ||||
| 17:00 | 0.770 | 9.93 | 0.068 | 12:00 | 0.045 | 6.33 | 0.21 | ||||
| 13:00 | 0.029 | 5.88 | 0.14 | ||||||||
| 15 April 2014 (1.213 mm/h) | 28 August 2013 (2.027 mm/h) | 20 July 2014 (2.013 mm/h) | 5 July 2013 (2.380 mm/h) | 28 August 2013 (2.647 mm/h) | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time | Flow | TN | TP | Time | Flow | TN | TP | Time | Flow | TN | TP | Time | Flow | TN | TP | Time | Flow | TN | TP |
| 6:00 | 0.0127 | 7.65 | 0.050 | 15:00 | 0.0375 | 1.13 | 0.13 | 19:00 | 0.0127 | 5.51 | 0.27 | 14:30 | 0.0127 | 5.03 | 0.06 | 19:00 | 0.03 | 5.59 | 0.05 |
| 6:30 | 0.024 | 12.27 | 0.412 | 15:30 | - | - | - | 19:30 | 0.0163 | 7.02 | 0.56 | 15:00 | - | - | - | 19:30 | 0.06 | 12.65 | 0.33 |
| 6:45 | 0.0375 | 11.49 | 0.366 | 16:00 | 0.0964 | 6.29 | 0.71 | 20:00 | 0.0485 | 6.92 | 0.86 | 15:30 | - | - | - | 20:00 | 1.78 | 15.24 | 1.39 |
| 7:00 | 0.0427 | 23.53 | 0.579 | 16:30 | 0.1020 | 5.57 | 0.3 | 20:30 | 0.1190 | 5.56 | 1.15 | 16:00 | 0.0127 | 8.81 | 1.50 | 20:30 | 2.22 | 16.38 | 0.84 |
| 7:15 | 0.0401 | 16.13 | 0.363 | 17:00 | 0.0964 | 5.81 | 0.32 | 21:00 | 0.0866 | 5.14 | 0.53 | 16:30 | 0.0127 | 6.37 | 2.56 | 21:00 | 1.94 | 13.88 | 0.69 |
| 7:30 | 0.0406 | 15.19 | 0.350 | 17:30 | 0.0547 | 5.2 | 0.2 | 21:30 | 0.0327 | 7.37 | 0.4 | 17:00 | 0.0375 | 1.06 | 2.11 | 21:30 | 0.80 | 14.95 | 0.44 |
| 8:00 | 0.0327 | 16.92 | 0.373 | 18:00 | 0.0427 | 4.95 | 0.14 | 22:00 | - | - | - | 17:30 | - | - | - | 22:00 | 0.39 | 13.43 | 0.55 |
| 8:30 | 0.0351 | 14.29 | 0.363 | 18:30 | - | - | - | 22:30 | 0.0375 | 5.64 | 0.24 | 18:00 | 0.4140 | - | - | 22:30 | 0.26 | 14.81 | 0.56 |
| 9:00 | 0.0327 | 11.26 | 0.291 | 19:00 | 0.0375 | 5.14 | 0.13 | 23:00 | - | - | 18:30 | 0.4440 | - | - | 23:00 | - | - | - | |
| 10:00 | - | - | - | 19:30 | - | - | - | 23:30 | 0.0182 | 6.49 | 0.19 | 19:00 | 0.2220 | 3.20 | 0.41 | 23:30 | - | - | - |
| 10:30 | 0.0351 | 8.67 | 0.228 | 20:00 | 0.0427 | 5.21 | 0.13 | 19:30 | - | - | - | 0:00 | - | - | - | ||||
| 11:00 | 0.0127 | 7.65 | 0.050 | 20:00 | 0.1590 | 4.08 | 0.28 | 0:30 | - | - | - | ||||||||
| 20:30 | - | - | - | 1:00 | 0.21 | 10.17 | 0.14 | ||||||||||||
| 21:00 | 0.0964 | 4.26 | 0.11 | 1:30 | - | - | - | ||||||||||||
| 21:30 | - | - | - | 2:00 | 0.15 | 9.83 | 0.19 | ||||||||||||
| 22:00 | 0.0775 | 3.78 | 0.22 | 2:30 | - | - | - | ||||||||||||
| 22:30 | - | - | - | 3:00 | 0.09 | 6.54 | 0.08 | ||||||||||||
| 23:00 | 0.0616 | 3.80 | 0.13 | ||||||||||||||||
| 23:30 | - | - | - | ||||||||||||||||
| 0:30 | 0.0547 | - | - | ||||||||||||||||
| 1:30 | 0.0427 | - | - | ||||||||||||||||
| Rainfall Events | Comprehensive Indicators K | |
|---|---|---|
| NPS-TP | NPS-TN | |
| 21 April 2014 | 0.986 | 0.953 |
| 24 July 2014 | 0.973 | 0.938 |
| 5 August 2014 | 0.958 | 0.921 |
| Rainfall Events | Comprehensive Indicators K | Traditional Indicators (NPS-TP) | |||
|---|---|---|---|---|---|
| NPS-TN | NPS-TP | Deviation | S | ||
| 15 April 2014 | 0.546 | 0.971 | 0.989 | 0.956 | 0.966 |
| 23 August 2014 | 0.937 | 0.924 | 0.934 | 0.892 | 0.943 |
| 20 July 2014 | 0.959 | 0.930 | 0.964 | 0.882 | 0.941 |
| 5 July 2013 | 0.340 | 0.948 | 0.997 | 0.908 | 0.938 |
| 28 August 2013 | 0.948 | 0.982 | 0.996 | 0.980 | 0.970 |
| Rainfall Events | Mean Load Deviation Percentage of Verification Points (%) | |
|---|---|---|
| NPS-TP | NPS-TN | |
| 15 April 2014 | 0.150 | 0.0770 |
| 23 August 2014 | 0.153 | 0.029 |
| 20 July 2014 | 0.041 | 0.094 |
| 5 July 2013 | 0.002 | 0.038 |
| 28 August 2013 | 0.120 | 0.022 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Sun, C.; Wang, G.; Xie, H.; Shen, Z. Modeling Multi-Event Non-Point Source Pollution in a Data-Scarce Catchment Using ANN and Entropy Analysis. Entropy 2017, 19, 265. https://doi.org/10.3390/e19060265
Chen L, Sun C, Wang G, Xie H, Shen Z. Modeling Multi-Event Non-Point Source Pollution in a Data-Scarce Catchment Using ANN and Entropy Analysis. Entropy. 2017; 19(6):265. https://doi.org/10.3390/e19060265
Chicago/Turabian StyleChen, Lei, Cheng Sun, Guobo Wang, Hui Xie, and Zhenyao Shen. 2017. "Modeling Multi-Event Non-Point Source Pollution in a Data-Scarce Catchment Using ANN and Entropy Analysis" Entropy 19, no. 6: 265. https://doi.org/10.3390/e19060265
APA StyleChen, L., Sun, C., Wang, G., Xie, H., & Shen, Z. (2017). Modeling Multi-Event Non-Point Source Pollution in a Data-Scarce Catchment Using ANN and Entropy Analysis. Entropy, 19(6), 265. https://doi.org/10.3390/e19060265