The Entropy of Words—Learnability and Expressivity across More than 1000 Languages

Abstract

The choice associated with words is a fundamental property of natural languages. It lies at the heart of quantitative linguistics, computational linguistics and language sciences more generally. Information theory gives us tools at hand to measure precisely the average amount of choice associated with words: the word entropy. Here, we use three parallel corpora, encompassing ca. 450 million words in 1916 texts and 1259 languages, to tackle some of the major conceptual and practical problems of word entropy estimation: dependence on text size, register, style and estimation method, as well as non-independence of words in co-text. We present two main findings: Firstly, word entropies display relatively narrow, unimodal distributions. There is no language in our sample with a unigram entropy of less than six bits/word. We argue that this is in line with information-theoretic models of communication. Languages are held in a narrow range by two fundamental pressures: word learnability and word expressivity, with a potential bias towards expressivity. Secondly, there is a strong linear relationship between unigram entropies and entropy rates. The entropy difference between words with and without co-textual information is narrowly distributed around ca. three bits/word. In other words, knowing the preceding text reduces the uncertainty of words by roughly the same amount across languages of the world.

1. Introduction

Symbols are the building blocks of information. When concatenated to strings, they give rise to surprisal and uncertainty, as a consequence of choice. This is the fundamental concept underlying information encoding. Natural languages are communicative systems harnessing this information-encoding potential. Their fundamental building blocks are words. For any natural language, the average amount of information a word can carry is a basic property, an information-theoretic fingerprint that reflects its idiosyncrasies, and sets it apart from other languages across the world. Shannon [1] defined the entropy, or average information content, as a measure for the choice associated with symbols in strings. Since Shannon’s [2] original proposal, many researchers have undertaken great efforts to estimate the entropy of written English with the highest possible precision [3,4,5,6] and to broaden the account to other natural languages [7,8,9,10,11].

Entropic measures in general are relevant for a wide variety of linguistic and computational subfields. For example, several recent studies engage in establishing information-theoretic and corpus-based methods for linguistic typology, i.e., classifying and comparing languages according to their information encoding potential [10,12,13,14,15,16], and how this potential evolves over time [17,18,19]. Similar methods have been applied to compare and distinguish non-linguistic sequences from written language [20,21], though it is controversial whether this helps with more fine-grained distinctions between symbolic systems and written language [22,23].

In the context of quantitative linguistics, entropic measures are used to understand laws in natural languages, such as the relationship between word frequency, predictability and the length of words [24,25,26,27], or the trade-off between word structure and sentence structure [10,13,28]. Information theory can further help to understand the complexities involved when building words from the smallest meaningful units, i.e., morphemes [29,30].

Beyond morphemes and word forms, the surprisal of words in co-text is argued to be related to syntactic expectations [31]. We use the term “co-text” here to refer to the purely linguistic, textual environment of a word type. This contrasts with the “context”, which can also include any non-linguistic environment associated with the word type, such as gestures, facial expression, or any multimodal perception in general. An example of a co-text effect is the usage of complementizers such as “that”, which might serve to smooth over maxima in the information density of sentences [32]. This has become known as the Uniform Information Density (UID) hypothesis. It was introduced in the 1980s by August and Gertraud Fenk [33], and developed in a series of articles (see [34] and the references therein). For a critical review of some problematic aspects of the UID hypothesis see [35,36].

In optimization models of communication, word entropy is a measure of cognitive cost [37]. These models shed light on the origins of Zipf’s law for word frequencies [38,39] and a vocabulary learning bias [40]. With respect to the UID hypothesis, these models have the virtue of defining explicitly a cost function and linking the statistical regularities with the minimization of that cost function.

Finally, in natural language processing, entropy (and related measures) have been widely applied to tackle problems relating to machine translation [41,42], distributional semantics [43,44,45,46], information retrieval [47,48,49] and multi-word expressions [50,51].

All of these accounts crucially hinge upon estimating the probability and uncertainty associated with different levels of information encoding in natural languages. Here, we focus on the word entropy of a given text and language. There are two central questions associated with this measure: (1) What is the text size (in number of tokens) at which word entropies reach stable values? (2) How much systematic difference do we find across different texts and languages? The first question is related to the problem of data sparsity. The minimum text size at which results are still reliable is a lower bound on any word entropy analysis. The second question relates to the diversity that we find across languages of the world. From the perspective of linguistic typology, we want to understand and explain this diversity.

In this study, we use state-of-the-art methods to estimate both unigram entropies [52] (for a definition see Section 3.2.6), and the entropy rate per word according to Gao et al. [5] (Section 3.2.7). Unigram entropy is the average information content of words assuming that they are independent of the co-text. The entropy rate can be seen, under certain conditions (see Section 3.2.7), as the average information content of words assuming that they depend on a sufficiently long, preceding co-text. For both measures we first establish stabilization points for big parallel texts in 21 and 32 languages respectively. Based on these stabilization points, we select texts with sufficiently large token counts from a massively parallel corpus and estimate word entropies across more than 1000 texts and languages. Our analyses illustrate two major points:

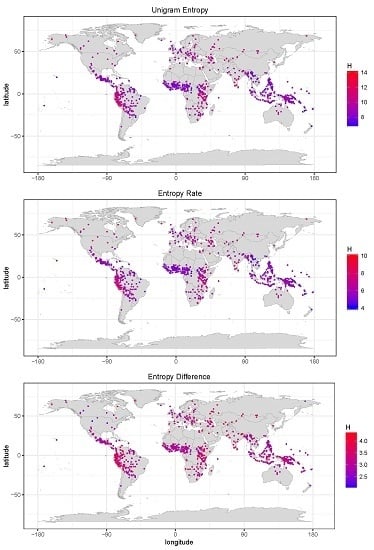
• Across languages of the world, unigram entropies display a unimodal distribution around a mean of ca. nine bits/word, with a standard deviation of ca. one bit/word. Entropy rates have a lower mean of ca. six bits/word, with a standard deviation of ca. one bit/word. Hence, there seem to be strong pressures keeping the mass of languages in a relatively narrow entropy range. This is particularly salient for the difference between unigram entropy and entropy rate (Section 5.2).
• There is a strong positive linear relationship between unigram entropies and entropy rates ($r=0.96,p<0.0001$). To our knowledge, this has not been reported before. We formulate a simple linear model that predicts the entropy rate of a text $\widehat{h}\left(T\right)$ from the unigram entropy ${\widehat{H}}_1\left(T\right)$ of the same text: $\widehat{h}\left(T\right)=k_1+k_2{\widehat{H}}_1\left(T\right)$, where $k_1=-1.12$ and $k_2=0.78$ (Section 5.3). The implication of this relationship is that uncertainty-reduction by co-textual information is approximately linear across languages of the world.

Clearly, higher or lower word entropy does not equate to “better” or “worse” communication systems in a very general sense. In any scenario where languages are used to communicate, a multitude of contextual cues (gestures, facial expression, general world knowledge, etc.) are integrated to give rise to meaning. Such contextual cues are typically not available in written language. However, in information-theoretic models of communication, the entropy of an inventory of symbols is the upper bound on mutual information between symbols and meanings (see Section 6.1). Thus, the entropy of words can be seen as the upper bound on expressivity in an information-theoretic sense.

We further argue in the discussion section that word entropies across languages of the world reflect the trade-off between two basic pressures on natural communication systems: word learnability vs. word expressivity. Hence, information-theoretic properties like entropy are not only relevant for computational linguistics and quantitative linguistics, but constitute a basic property of human languages. Understanding and modelling the differences and similarities in the information that words can carry is an undertaking at the heart of language sciences more generally.

2. Data

To estimate the entropy of words, we first need a comparable sample of texts across many languages. Ideally, the texts should have the same content, as differences in registers and style can interfere with the range of word forms used, and hence the entropy of words [53]. To control for constant content across languages, we use three sets of parallel texts: (1) the European Parliament Corpus (EPC) [54], (2) the Parallel Bible Corpus (PBC) [55] (last accessed on 2 June 2016), and the Universal Declaration of Human Rights (http://www.unicode.org/udhr/). Details about the corpora can be seen in

Table 1. Information on the parallel corpora used.

Corpus	Register	Size *	Mean Size *	Texts	Lang
EPC	Political	ca. 21 M	ca. 1 M	21	21
PBC	Religious	ca. 430 M	ca. 290 K	1525	1137
UDHR	Legal	ca. 500 K	ca. 1.3 K	370	341
	Total:	ca. 450 M		1916	1259

* In number of tokens.

. The general advantage of the EPC is that it is big in terms of numbers of word tokens per language (ca. 30 M) (though we only use around one M tokens for each language, since this is enough for the stabilization analyses), whereas the PBC and the UDHR are smaller (ca. 290 K and 1.3 K word tokens per language). However, the PBC and UDHR are massively parallel in terms of encompassing more than 1000 and more than 300 languages, respectively. These are numbers of texts and languages that we actually used for our analyses. The raw corpora are bigger. However, some texts and languages had to be excluded due to their small size, or due to pre-processing errors (see Section 3.1).

3. Theory

3.1. Word Types and Tokens

The basic information encoding unit chosen in this study is the word. In contrast, most earlier studies on the entropy of languages [2,4,6] chose characters instead. A word type is here defined as a unique string of alphanumeric UTF-8 characters delimited by white spaces. All letters are converted to lower case and punctuation is removed. A word token is then any reoccurrence of a word type. For example, the pre-processed first verse of the Book of Genesis in English reads:

in the beginning god created the heavens and the earth and the earth was waste and empty [...]

The set of word types (in lower case) for this sentence is:

$$\mathcal{V}=\{in,the,beginning,god,created,heavens,and,earth,was,waste,empty\}.$$

(1)

Hence, the number of word types in this sentence is 11, but the number of word tokens is 17, since the, and and earth occur several times. Note that some scripts, e.g., those of Mandarin Chinese (cmn) and Khmer (khm), delimit phrases and sentences by white spaces, rather than words. Such scripts have to be excluded for the simple word processing we propose. However, they constitute a negligible proportion of our sample (≈0.01%). In fact, ca. 90% of the texts are written in Latin-based script. For more details and caveats of text pre-processing, see Appendix A.

Though definitions of “word-hood” based on orthography are common in corpus and computational linguistic studies, they are somewhat controversial within the field of linguistic typology. Haspelmath [56] and Wray [57], for instance, point out that there is a range of orthographic, phonetic and distributional definitions for the concept “word”, which can yield different results across different cases. However, a recent study on compression properties of parallel texts vindicates the usage of orthographic words as information encoding units, as it shows that these are optimal-sized for describing the regularities in languages [58].

Hence, we suggest to start with the orthographic word definition based on non-alphanumeric characters in written texts; not the least because it is a computationally feasible strategy across many hundreds of languages. Our results might then be tested against more fine-grained definitions, as long as these can be systematically applied to language production data.

3.2. Entropy Estimation

3.2.1. General Conditions

The conditions (e.g., the sample size) under which the entropy of a source can be estimated reliably are a living field of research ([59,60] and the references therein). Proper estimation of entropy requires certain conditions to be met. Stationarity and ergodicity are typically named as such. Stationarity means that the statistical properties of blocks of words do not depend on their position in the text sequence. Ergodicity means that statistical properties of a sufficiently long text sequence match the average properties of the ensemble of all possible text sequences. (e.g., [59,61]). Another condition is finiteness (i.e., a corpus has a finite set of word types). While stationarity and ergodicity tend to be presented and discussed together in research articles, finiteness is normally stated separately, typically as part of the initial setting of the problem (e.g., [59,61]). A fourth usual condition is the assumption that types are independent and identically distributed (i.i.d.) [59,61,62]. Hence, for proper entropy estimation the typical requirements are either (a) finiteness, stationarity and ergodicity, or (b) only finiteness and i.i.d., as stationarity and ergodicity follow trivially from the i.i.d. assumption.

3.2.2. Word Entropy Estimation

A crucial pre-requisite for entropy estimation is the approximation of the probabilities of word types. In a text, each word type $w_i$ has a token frequency $f_i=freq\left(w_i\right)$. Take the first verse of the English Bible again.

in the beginning god created the heavens and the earth and the earth was waste and empty [...]

In this example, the word type the occurs four times, and occurs three times, etc. As a simple approximation, $p\left(w_i\right)$ can be estimated via the so-called maximum likelihood method [63]:

$$\widehat{p}\left(w_i\right)=\frac{f_i}{{\sum }_{j=1}^V{f}_j},$$

(2)

where the denominator is the overall number of word tokens, i.e., the sum of type frequencies over an empirical (i.e., finite) vocabulary of size $V=\left|\mathcal{V}\right|$. We thus have probabilities of $\widehat{p}\left(the\right)=\frac{4}{17}$, $\widehat{p}\left(and\right)=\frac{3}{17}$, etc.

Assume a text is a random variable T created by a process of drawing (with replacement) and concatenating tokens from a set (or vocabulary) of word types $\mathcal{V}=\{w_1,w_2,...,w_W\}$, where W is the (potentially infinite) theoretical vocabulary size, and a probability mass function $p\left(w\right)=Pr\{T=w\}$ for $w\in \mathcal{V}$. Given these definitions, the theoretical entropy of T can be calculated as [64]:

$$H\left(T\right)=-\sum _{i=1}^{W}p\left(w_i\right){log}_{2}p\left(w_i\right).$$

(3)

In this case, $H\left(T\right)$ can be seen as the average information content of word types. A crucial step towards estimating $H\left(T\right)$ is to reliably approximate the probabilities of word types $p\left(w_i\right)$.

The simplest way to estimate $H\left(T\right)$ is the maximum likelihood estimator, also called the plug-in estimator, which is obtained replacing $p\left(w\right)$ by $\widehat{p}\left(w\right)$ (Equation (2)). For instance, our example “corpus” yields:

$$\widehat{H}\left(T\right)=-\left(\frac{4}{17}{log}_2\left(\frac{4}{17}\right)+\frac{3}{17}{log}_2\left(\frac{3}{17}\right)+\cdots +\frac{1}{17}{log}_2\left(\frac{1}{17}\right)\right)\approx 3.2bits/word.$$

(4)

Notice an important detail: we have assumed that $p\left(w_i\right)=\widehat{p}\left(w_i\right)=0$ for all the types that have not appeared in our sample. Although our sample did not contain “never”, the probability of “never” in an English text is not zero. We have also assumed that the relative frequency of the words that have appeared in our sample is a good estimation of their true probability. Given the small size of our sample, this is unlikely to be the case. The bottom line is that for small text sizes we will underestimate the word entropy using the maximum likelihood approach [62,65]. A range of more advanced entropy estimators have been proposed to overcome this limitation [6,52,61,63]. These are outlined in more detail in Appendix B, and tested with our parallel corpus data.

However, even with advanced entropy estimators, there are two fundamental problems: (1) the set of word types in natural languages is non-finite, (2) tokens are not i.i.d., since they exhibit short- and long-range correlations. These issues are discussed in the following.

3.2.3. Problem 1: The Infinite Productive Potential of Languages

The first problem relates to the productive potential of languages. In fact, it is downright impossible to capture the actual repertoire of word types in a language. Even if we captured the whole set of linguistic interactions of a speaker population in a massive corpus, we would still not capture the productive potential of the language beyond the finite set of linguistic interactions.

Theoretically speaking, it is always possible to expand the vocabulary of a language by compounding (recombining word types to form new word types), affixation (adding affixes to existing words), or by creating neologisms. This can be seen in parallel to Chomsky’s ([66], p. 8) reappraisal of Humboldt’s “make infinite use of finite means” in syntax. The practical consequence is that even for massive corpora like the British National Corpus, vocabulary growth is apparently not coming to a halt [67,68,69]. Thus, we never actually sample the whole set of word types of a language. However, current entropy estimators are developed only for a finite “alphabet” (i.e., repertoire of word types in our case). Note that the concentration of tokens on a core vocabulary [68,70] potentially alleviates this problem. Still, word entropy estimation is a harder problem than entropy estimation for characters or phoneme types, since the latter have a repertoire that is finite and usually small.

3.2.4. Problem 2: Short- and Long-Range Correlations between Words

In natural languages, we find co-occurrence patterns illustrating that word types in a text sequence are not independent events. This is the case for collocations, namely blocks of consecutive words that behave as a whole. Examples include place names such as “New York” or fixed expressions such as “kith and kin”, but also many others that are less obvious. They can be detected with methods determining if some consecutive words co-occur with a frequency that is higher than expected by chance [71]. Collocations are examples of short-range correlations in text sequences. Text sequences also exhibit long-range correlations, i.e., correlations between types that are further apart in the text [8,72].

3.2.5. Our Perspective

We are fully aware of both Problems 1 and 2 when estimating the word type entropy of real texts, and the languages represented by them. However, our question is not so much: what is the exact entropy of a text or language? but rather: How precisely do we have to approximate it to make a meaningful cross-linguistic comparison possible? To address this practical question, we need to establish the number of word tokens at which estimated entropies reach stable values, given a threshold of our choice. Furthermore, we incorporate entropic measures which are less demanding in terms of assumptions. Namely, we include h, the entropy rate of a source, as it does not rely on the i.i.d. assumption. We elaborate on h in the next two subsections.

3.2.6. n-Gram Entropies

When estimating entropy according to Equation (3), we assume unigrams, i.e., single, independent word tokens, as “blocks” of information encoding. As noted above, this assumption is generally not met for natural languages. To incorporate dependencies between words, we could use bigrams, trigrams, or more generally n-grams of any size, and thus capture short- and long-range correlations by increasing “block” sizes to 2, 3, n. This yields what are variously called n-gram or block entropies [6], defined as:

$${\displaystyle H_n\left(T\right)=-\sum _{i=1}^{W^n}p({g_i}^{\left(n\right)})\times {log}_{2}p({g_i}^{\left(n\right)}),}$$

(5)

where n is the block size, $p\left({g_i}^{\left(n\right)}\right)$ is the probability of an n-gram $g_i$ of block size n, and $W^n$ is the potentially infinite size of the “alphabet” of n-grams. However, since the number of different n-grams grows exponentially with n, very big corpora are needed to get reliable estimates. Schürmann and Grassberger [6] use an English corpus of 70 M words, and assert that entropy estimation beyond a block size of five characters (not words) is already unreliable. Our strategy is to stick with block sizes of one, i.e., unigram entropies. However, we implement a more parsimonious approach to take into account long-range correlations between words along the lines of earlier studies by Montemurro and Zanette [8,9].

3.2.7. Entropy Rate

Instead of calculating $H_n\left(T\right)$ with ever increasing block sizes n, we use an approach focusing on a particular feature of the entropy growth curve: the so-called entropy rate, or per-symbol entropy [5]. In general, it is defined as the rate at which the word entropy grows as the number of word tokens N increases ([73], p. 74), i.e.,

$$h\left(T\right)=\underset{N\to \infty }{lim}\frac{1}{N}{H}_n\left(T\right)=\underset{N\to \infty }{lim}\frac{1}{N}H(t_1,t_2,...,t_N),$$

(6)

where $t_1,t_2,...,t_N$ is a block of consecutive tokens of length N. Given stationarity, this is equivalent to ([73], p. 75)

$$h\left(T\right)=\underset{N\to \infty }{lim}H\left(t_N\right|t_1,t_2,...,t_{N-1}).$$

(7)

In other words, as the number of tokens N approaches infinity, the entropy rate $h\left(T\right)$ reflects the average information content of a token $t_N$ conditioned on all preceding tokens. Therefore, $h\left(T\right)$ accounts for all statistical dependencies between tokens [61]. Note that in the limit, i.e., as block size n approaches infinity, the block entropy per token converges to the entropy rate. Furthermore, for an independent and identically distributed (i.i.d) random variable, the block entropy of block size one, i.e., $H_1\left(T\right)$, is identical to the entropy rate [61]. However, as pointed out above, in natural languages words are not independently distributed.

Kontoyiannis et al. [4] and Gao et al. [5] apply findings on optimal compression by Ziv and Lempel [74,75] to estimate the entropy rate. More precisely, Gao et al. [5] show that entropy rate estimation based on the so-called increasing window estimator, or LZ78 estimator [73], is efficient in terms of convergence. The conditions for this estimator are stationarity and ergodicity of the process that generates a text T. Again, its consistency has only been proven for a finite alphabet (i.e., finite set of word types in our case).

Applied to the problem of estimating word entropies, the method works as follows: for any given word token $t_i$ find the longest match-length $L_i$ for which the token string $s_i^{i+l-1}=(t_i,t_{i+1},...,t_{i+l-1})$ matches a preceding token string of the same length in $(t_1,...,t_{i-1})$. Formally, we define $L_i$ as:

$$L_i=1+max\{0\le l\le i:s_i^{i+l-1}=s_j^{j+l-1}\mathrm{for}\mathrm{some}0\le j\le i-1\}.$$

(8)

This is an adaptation of Gao et al.’s [5] match-length definition (note that Gao et al. [5] give a more general definition that also holds for the so-called sliding window, or LZ77 estimator). To illustrate this, take the example from above again:

in₁ the₂ beginning₃ god₄ created₅ the₆ heavens₇ and₈ the₉ earth₁₀ and₁₁ the₁₂ earth₁₃ was₁₄ waste₁₅ and₁₆ empty₁₇ [...]

For the word token beginning, in position $i=3$, there is no match in the preceding token string (in the). Hence, the match-length is $L_3=0(+1)=1$. In contrast, if we look at and in position $i=11$, then the longest matching token string is and the earth. Hence, the match-length is $L_{11}=3(+1)=4$.

Note that the average match-lengths across all word tokens reflect the redundancy in the token string, which is the inverse of unpredictability or choice. Based on this connection, Gao et al. [5], Equation (6), show that the entropy rate of a text can be approximated as:

$${\displaystyle \widehat{h}\left(T\right)=\frac{1}{N}\sum _{i=2}^N\frac{{log}_{2}i}{L_i},}$$

(9)

where N is the overall number of tokens, and i is the position in the string. Here, we approximate the entropy rate $h\left(T\right)$ based on a text T as $\widehat{h}\left(T\right)$ given in Equation (9).

4. Methods

4.1. Entropy Estimation Software

We estimate unigram entropies, i.e., entropies for block sizes of one ($H_1\left(T\right)$), with nine different estimation methods, using the R package entropy [76], and the Python implementation of the Nemenman–Shafee–Bialek (NSB) [52] estimator (https://gist.github.com/shhong/1021654/). For further analyses, we especially focus on the NSB estimator, as it has been shown to have a faster convergence rate compared to other block entropy estimators [63]. Moreover, we implemented the entropy rate estimator $\widehat{h}\left(T\right)$ as in Gao et al.’s [5] proposal in both Python and R, available on github (https://github.com/dimalik/Hrate/). This was inspired by an earlier implementation by Montemurro and Zanette [8] of Kontoyiannis et al.’s [4] estimator.

4.2. Stabilization Criterion

When estimating entropy with increasingly longer “prefixes” (i.e., runs of text preceding a given token) a fundamental milestone is convergence, namely, the prefix length at which the true value is reached with an error that can be neglected. However, the “true” entropy of a productive system like natural language is not known. For this reason, we replace convergence by another important milestone: the number of tokens at which the next 10 estimations of entropy have a SD (standard deviation) that is sufficiently small, e.g., below a certain threshold. If N is the number of tokens, SD is defined as the standard deviation that is calculated over entropies obtained with prefixes of lengths:

$$N,N+1K,N+2K,...,N+10K.$$

(10)

K represents the number 1000 here. We say that entropies have stabilized when SD $<\alpha$, where $\alpha$ is the threshold. Notice that this is a local stabilization criterion. Here, we choose N to run from $1K$ to $90K$. We thus get 90 SD values per language. The threshold is $\alpha =0.1$. The same methodology is used to determine when the entropy rate has stabilized.

Two earlier studies, Montemurro and Zanette [8] and Koplenig et al. [10], use a more coarse-grained stabilization criterion. In [8] entropies are estimated for two halves of each text, and then compared to the entropy of the full text. Only texts with a maximum discrepancy of 10% are included for further analyses. Similarly, [10] compares entropies for the first 50% of the data and for the full data. Again, only texts with a discrepancy of less then 10% are included. In contrast, [11] establishes the convergence properties of different off-the-shelf compressors by estimating the encoding rate with growing text sizes. This has the advantage of giving a more fine-grained impression of convergence properties. Our assessment of entropy stabilization follows a similar rationale, though with words as information encoding units, rather than characters, and with our own implementation of Gao et al.’s entropy estimator rather than off-the-shelf compressors.

4.3. Corpus Samples

To assess the minimum text sizes at which both unigram entropies and entropy rates stabilize, we use 21 languages of the European Parliament Corpus (EPC), as well as a subset of 32 languages from different language families of the Parallel Bible Corpus (Section 5.1).

For estimating unigram entropies and entropy rates across languages of the world, we use the full PBC. Based on our stabilization analyses, we choose a conservative cut-off point: only texts with at least 50 K tokens are included. Of these, in turn, we take the first 50 K tokens for estimation. This criterion reduces the original PBC sample of 1525 texts and 1137 languages (ISO 639-3 codes) to 1499 texts and 1115 languages. This sample is used in Section 5.2 and Section 5.3.

5. Results

5.1. Entropy Stabilization throughout the Text Sequence

For both unigram entropies and entropy rates, the stabilization criterion, i.e., SD < 0.1, is met at 50 K tokens. This is the case for the 21 languages of the European Parliament Corpus (EPC) (Appendix C), as well as the 32 languages of the Parallel Bible Corpus (Appendix D). The UDHR texts are generally too small (ca. 1300 tokens on average) for stabilization.

Additionally, Appendix E illustrates that there are generally strong correlations between different entropy estimation methods, despite differences in stabilization properties. Appendix G gives Pearson correlations between unigram entropies of the PBC, EPC, and the UDHR. These are also strong (around $0.8$), despite the differences in registers and styles, as well as text sizes. In sum, our analyses converge to show that entropy rankings of languages are stable at ca. 50 K tokens.

5.2. Word Entropies across More than 1000 Languages

Figure 1a shows a density plot of the estimated entropic values across all 1499 texts and 1115 languages of the PBC sample. Both unigram entropies and entropy rates show a unimodal distribution that is skewed to the right. Unigram entropies are distributed around a mean of $9.14$ ($SD=1.12$), whereas entropy rates have a lower mean of $5.97$ ($SD=0.91$). In Figure 1b, it is clearly visible that the difference between unigram entropies and entropy rates has a narrower distribution: it is distributed around a mean of ca. 3.17 bits/word with a standard deviation of $0.36$.

To visually illustrate the diversity of entropies across languages of the world, Figure 2 gives a map with unigram entropies, entropy rates and the difference between them. The range of entropy values in bits per word is indicated by a colour scale from blue (low entropy) to red (high entropy). As can be seen in the upper map, there are high and low entropy areas across the world, further discussed below. A similar pattern holds for entropy rates (middle panel), though they are generally lower. The difference between unigram entropies and entropy rates, on the other hand, is even more narrowly distributed (as seen also in Figure 1b) and the colours are almost indistinguishable.

5.3. Correlation between Unigram Entropy and Entropy Rate

The density plot for unigram entropies in Figure 1 looks like a slightly wider version of the entropy rate density plot, just shifted to the right of the scale. This suggests that unigram entropies and entropy rates might be correlated. Figure 3 confirms this by plotting unigram entropies on the x-axis versus entropy rates on the y-axis for each given text. The linearity of the relationship tends to increase as text length increases (from 30 K tokens onwards) as shown in Figure 4. This holds for all entropy estimators since they are strongly correlated (Appendix E).

In Appendix F we also give correlations between unigram entropy values for all nine estimation methods and entropy rates. The Pearson correlations are strong (between $r=0.95$ and $r=0.99$, with $p<0.0001$). Hence, despite the conceptual difference between unigram entropies and entropy rates, there is a strong underlying connection between them. Namely, a linear model fitted (with the package lme4 in R [77]) through the points in Figure 3 (left panel) can be specified as:

$$\widehat{h}\left(T\right)=-1.12+0.78{\widehat{H}}_1\left(T\right).$$

(11)

The intercept of $-1.12$ is significantly smaller than zero ($p<0.0001$), and the linear coefficient of $0.78$ is significantly smaller than one ($p<0.0001$). Via Equation (11), we can convert unigram entropies into entropy rates with a variance of $0.035$. Hence, the observed difference of ca. 3.17 bits/word between unigram entropies and entropy rates (see Figure 1) is due to the interaction of two constants: First, there is a fixed difference of ca. 1.12 bit/word between the two estimators and a variable reduction of ca. 22% when converting unigram entropies into entropy rates (22% of the mean 9.14 bit/word for unigram entropies amounts to ca. 2.0 bit/word on average). More generally, for natural languages word entropy rates $\widehat{h}\left(T\right)$ and unigram entropies ${\widehat{H}}_1\left(T\right)$ are linked by a linear relationship:

$$\widehat{h}\left(T\right)=k_1+k_2{\widehat{H}}_1\left(T\right),$$

(12)

where $k_1$ and $k_2$ are constants. The exact meaning and implications of these constants are topics for future research.

The right panels of Figure 3 plot the same relationship between unigram entropies and entropy rates faceted by geographic macro areas taken from Glottolog 2.7 [78]. These macro areas are generally considered relevant from a linguistic typology point of view. It is apparent from this plot that the linear relationship extrapolates across different areas of the world.

6. Discussion

6.1. Entropy Diversity across Languages of the World

In Section 5.2, we estimated word entropies for a sample of more than 1000 languages of the PBC. We find that unigram entropies cluster around a mean value of about nine bits/word, while entropy rates are generally lower, and fall closer to a mean of six bits/word (Figure 1). This is to be expected, since the former do not take co-textual information into account, whereas the latter do. To see this, remember that under stationarity, the entropy rate can be defined as a word entropy conditioned on a sufficiently large number of previous tokens (Equation (7)), while the unigram entropy is not conditioned on the co-text. As conditioning reduces entropy [73], it is not surprising that entropy rates tend to fall below unigram entropies.

It is more surprising that given the wide range of potential entropies, from zero to ca. 14, most natural languages fall on a relatively narrow spectrum. It is non-trivial to find an upper limit for the maximum word entropy of natural languages. In theory, it could be infinite given that the range of word types is potentially infinite. However, in practice the highest entropy languages range only up to ca. 14 bits/word. Unigram entropies mainly fall in the range between seven to 12 bits/word, and entropy rates in the range between four to nine bits/word. Thus, each only covers around 40% of the scale. The distributions are also skewed to the right, and seem to differ from the Gaussian, and therefore symmetric, distribution that is expected for the plug-in estimator under a two-fold null hypothesis: (1) that the true entropy is the same for all languages, and that (2) besides the bias in the entropy estimation, there is no additional bias constraining the distribution of entropy [62]. It needs to be clarified in further studies where this right-skewness stems from.

Overall, the distributions suggest that there are pressures at play which keep word entropies in a relatively narrow range. We argue that this observation is related to the trade-off between the learnability and expressivity of communication systems. A (hypothetical) language with maximum word entropy would have a vast (potentially infinite) number of word forms of equal probability, and would be hard (or impossible) to learn. A language with minimum word entropy, on the other hand, would repeat the same word forms over and over again, and lack expressivity. Natural languages fall in a relatively narrow range between these extremes. This is in line with evidence from iterated learning experiments and computational simulations. For instance, Kirby et al. [79] illustrate how artificial languages collapse into states with underspecified word/meaning mappings, i.e., low word entropy states, if only pressure for learnability is given. On the other hand, when only pressure for expressivity is given, then so-called holistic strategies evolve with a separate word form for each meaning, i.e., a high word entropy state. However, if both pressures for learnability and expressivity interact then combinatoriality emerges as a coding strategy, which keeps unigram word entropies in the middle ground.

This trade-off is also obvious in optimization models of communication, which are based on two major principles: entropy minimization and maximization of mutual information between meanings and word forms [40]. Zipf’s law for word frequencies, for instance, emerges in a critical balance between these two forces [39]. In these models, entropy minimization is linked with learnability: fewer word forms are easier to learn (see [80] for other cognitive costs associated with entropy). Whereas mutual information maximization is linked with expressivity via the form/meaning mappings available in a communication system. Note that a fundamental property in information theoretic models of communication is that $MI$, the mutual information between word forms and meanings, cannot exceed the entropy, i.e., [37]

$$MI\le H$$

(13)

The lower the entropy, the lower the potential for expressivity. Hence, the entropy of words is an upper bound on the expressivity of words. This may also shed light on the right-skewness of the unigram entropy distribution in Figure 1. Displacing the distribution to the left or skewing it towards low values would compromise expressivity. In contrast, skewing it towards the right increases the potential for expressivity according to Equation (13), though this comes with a learnability cost.

Further support for pressure to increase entropy to warrant sufficient expressivity (Equation (13)) comes from the fact that there is no language with less than six bits/word unigram entropy for neither the PBC nor the EPC. There is only one language in the UDHR that has a slightly lower unigram entropy, a Zapotecan language of Meso-America (zam). It has a fairly small corpus size (1067 tokens), and the same language has more than eight bits/word in the PBC. Thus, there is no language which is more than three SDs below the mean of unigram entropies. On the other hand, there are several languages that are more than four SDs higher than the mean, i.e., around or beyond 13 bits/word.

Despite the fact that natural languages do not populate the whole range of possible word entropies, there can still be remarkable differences. Some of the languages at the low-entropy end are Tok Pisin, Bislama (Creole languages), and Sango (Atlantic-Congo language of Western Africa). These have unigram entropies of around 6.7 bits/word. Languages to the high-end include Greenlandic Inuktitut and Ancient Hebrew, with unigram entropies around 13 bits/word. Note that this is not to say that Greenlandic Inuktitut or Ancient Hebrew are “better” or “worse” communication systems than Creole languages or Sango. Such an assessment is misleading for two reasons: First, information encoding happens in different linguistic (and non-linguistic) dimensions, not just at the word level. We are only just starting to understand the interactions between these levels from an information-theoretic perspective [10]. Second, if we assume that natural languages are used for communication, then both learnability and expressivity of words are equally desirable features. Any combination of the two arises in the evolution of languages due to adaptive pressures. There is nothing “better” or “worse” about learnability or expressivity per se.

On a global scale, there seem to be high and low entropy areas. For example, languages in the Andean region of South America all have high unigram entropies (bright red in Figure 2). This is most likely due to their high morphological complexity, resulting in a wide range of word types, which were shown to correlate with word entropies [81]. Further areas of generally high entropies include Northern Eurasia, Eastern Africa, and North America. In contrast, Meso-America, Sub-Saharan Africa und South-East Asia are areas of relatively low word entropies (purple and blue in Figure 2). Testing these global patterns for statistical significance is an immediate next step in our research. Some preliminary results for unigram entropies and their relationship with latitude can be found in [14].

We are just beginning to understand the driving forces involved when languages develop extremely high or low word entropies. For example, Bentz et al. [12] as well as Bentz and Berdicevskis [18] argue that specific learning pressures reduce word entropy over time. As a consequence, different scenarios of language learning, transmission and contact might lead to global patterns of low and high entropy areas [14].

6.2. Correlation between Unigram Entropies and Entropy Rates

In Section 5.3, we found a strong correlation between unigram entropies and entropy rates. This is surprising, as we would expect that the co-text has a variable effect on the information content of words, and that this might differ across languages too. However, what we actually find is that the co-text effect is (relatively) constant across languages. To put it differently, knowing the co-text of words decreases their uncertainty, or information content, by roughly the same amount, regardless of the language. Thus, entropy rates are systematically lower than unigram entropies, by 3.17 bits/word on average.

Notably, this result is in line with earlier findings by Montemurro and Zanette [8,9]. They have reported, for samples of eight and 75 languages respectively, that the difference between word entropy rates for texts with randomized word order and those of texts with original word order is about $3.5$ bits/word. Note that the word entropy rate given randomized word order is conceptually the same as unigram entropies, since any dependencies between words are destroyed via randomization [8] (technically all the tokens of the sequence become independent and identically distributed variables ([73], p. 75). Montemurro and Zanette [8,9] also show that while the average information content of words might differ across languages, the co-text reduces the information content of words by a constant amount. They interpret this as a universal property of languages. We have shown for a considerably bigger sample of languages that the entropy difference has a smaller variance than the original unigram entropies and entropy rates, which consistent with Montemurro and Zanette’s findings (Figure 1).

As a consequence, the entropy rate is a linear function of unigram entropy, and can be straightforwardly predicted from it. To our knowledge, we have provided the first empirical evidence for a linear dependency between the entropy rate and unigram entropy (Figure 3). Interestingly, we have shown that this linearity of the relationship increases as text length increases (Figure 4). A mathematical investigation of the origins of this linear relationship should be the subject of future research.

There is also a practical side to this finding: estimating entropy rates requires searching strings of length $i-1$, where i is the index running through all tokens of a text. As i increases, the CPU time per additional word token increases linearly. In contrast, unigram entropies can be estimated based on dictionaries of word types and their token frequencies, and the processing time per additional word token is constant. Hence, Equation (11) can help to reduce processing costs considerably.

7. Conclusions

The entropy, average information content, uncertainty or choice associated with words is a core information-theoretic property of natural languages. Understanding the diversity of word entropies requires an interdisciplinary discourse between information theory, quantitative linguistics, computational linguistics, psycholinguistics, language typology, as well as historical and evolutionary linguistics.

As a first step, we have here established word entropy stabilization points for 21 languages of the European Parliament Corpus and 32 languages of the Parallel Bible Corpus. We illustrated that word entropies can be reliably estimated with text sizes of >50 K. Based on these findings, we estimated entropies across 1499 texts and 1115 languages of the Parallel Bible Corpus. These analyses shed light on both the diversity of languages and the underlying universal pressures that shape them. While the information encoding strategies of individual languages might vary considerably across the world, they all need to adhere to fundamental principles of information transfer. In this context, word learnability and word expressivity emerge as fundamental constraints on language variation. In some scenarios of learning and usage, the pressure to be expressive might be systematically stronger than the pressure to be learnable.

Furthermore, we have shown that there is a strong linear relationship between unigram entropies and their entropy rates, which holds across different macro areas of the world’s languages. The theoretical implication of this finding is that co-text effects on the predictability of words are relatively similar regardless of the language in consideration. The practical implication is that entropy rates can be approximated by using unigram entropies, thus reducing processing costs.