Thermal Transport and Entropy Production Mechanisms in a Turbulent Round Jet at Supercritical Thermodynamic Conditions
Abstract
:1. Introduction
2. Thermophysical Formulation
2.1. Balance Equations
2.2. Thermodynamic and Transport Models
2.3. Entropy Principle and Irreversibility
3. Configuration and Numerical Procedure
3.1. Test Case
3.2. Computational Setup
3.3. Numerical Procedure
4. Results
4.1. Summary of the Previous Study in [26]
4.2. Thermal Transport
4.3. Entropy Production
5. Conclusions
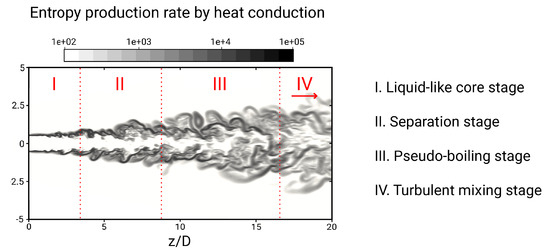
- I
- Liquid-like core stage:The liquid-like core of the jet is almost unaffected by the surrounding. At this stage, mean temperature along the centerline remains constant, and the root-mean-square temperate is zero. The entropy production is quite small.
- II
- Separation stage:Dense pockets of liquid-like fluid are separated from the core, inducing additional shearing and temperature gradients. At this stage, both entropy production rates by heat transport and by viscous dissipation increase along the centerline.
- III
- Pseudo-boiling stage:Dense pockets tend to smear out, and pseudo-boiling takes place. Absorbed heat is primarily used to overcome intermolecular cohesion. Accordingly, shearing is reduced, and entropy production by heat transfer increases.
- IV
- Turbulent mixing stage:Most of the liquid-like nitrogen is pseudo-evaporated, and turbulent mixing dominates. While the temperature increases, the entropy production rates decrease.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Messerschmid, L.; Fasoulas, S. Raumfahrtsysteme, 4rd ed.; Springer-Verlag: Berlin, Germany, 2011. [Google Scholar]
- Knez, Ž.; Markočič, E.; Leitgelb, M.; Primožič, M.; Knez Hrnčič, M.; Škerget, M. Industrial applications of supercritical fluids: A review. Energy 2014, 77, 235–243. [Google Scholar] [CrossRef]
- Ahn, Y.; Bae, S.J.; Kim, M.; Cho, S.K.; Baik, S.; Lee, J.I.; Cha, J.E. Review of supercritical CO2 power cycle technology and current status of research and development. Nucl. Eng. Technol. 2015, 47, 647–661. [Google Scholar] [CrossRef]
- Kumar, S.; Chauhan, M.K.; Varun. Numerical modeling of compression ignition engine: A review. Renew. Sust. Energ. Rev. 2013, 19, 517–530. [Google Scholar] [CrossRef]
- Banuti, D.T. Crossing the Widom-line—Supercritical pseudo-boiling. J. Supercrit. Fluid 2015, 98, 12–16. [Google Scholar] [CrossRef]
- Sadiki, A.; Hutter, K. On thermodynamics of turbulence: Development of first order closure models and critical evaluation of existing models. J. Non-Equilib. Thermodyn. 2000, 25, 131–160. [Google Scholar] [CrossRef]
- Bejan, A. Second-law analysis in heat transfer and thermal design. Adv. Heat Transf. 1982, 15, 1–58. [Google Scholar]
- Bejan, A. Entropy Generation Minimization: The Method of Thermodynamic Optimization of Finite-Size Systems and Finite-Time Processes; CRC Press LLC: Boca Raton, FL, USA, 1995. [Google Scholar]
- Som, S.K.; Datta, A. Thermodynamic irreversibilities and exergy balance in combustion processes. Prog. Energ. Cumbust. 2008, 34, 351–376. [Google Scholar] [CrossRef]
- Oztop, H.F.; Al-Salem, K. A review on entropy generation in natural and mixed convection heat transfer for energy systems. Renew. Sust. Energ. Rev. 2012, 16, 911–920. [Google Scholar] [CrossRef]
- Ko, T.H.; Wu, C.P. A numerical study on entropy generation induced by turbulent forced convection in curved rectangular ducts with various aspect ratios. Int. Commun. Heat Mass 2009, 36, 25–31. [Google Scholar] [CrossRef]
- Sciacovelli, A.; Verda, V.; Sciubba, E. Entropy generation analysis as a design tool-A review. Renew. Sust. Energ. Rev. 2015, 43, 1167–1181. [Google Scholar] [CrossRef]
- Ahmadi, G. A two-equation turbulence model for compressible flows based on the second law of thermodynamics. J. Non-Equilib. Thermodyn. 1989, 14, 49–59. [Google Scholar] [CrossRef]
- Sadiki, A. Extended thermodynamics as modeling tool of turbulence in fluid flows. In Trends in Applications of Mathematics to Mechanics; Wang, Y., Hutter, K., Eds.; Shaker Verlag: Aachen, Germany, 2005. [Google Scholar]
- Sierra-Pallares, J.; del Velle, J.G.; García-Carrascal, P.; Ruiz, F.C. Numerical study of supercritical and transcritical injection using different turbulent Prandlt numbers: A second law analysis. J. Supercrit. Fluid 2016, 115, 86–98. [Google Scholar] [CrossRef]
- Okong’o, N.A.; Bellan, J. Direct numerical simulations of transitional supercritical binary mixing layers: Heptane and nitrogen. Int. J. Fluid Mech. 2002, 464, 1–34. [Google Scholar] [CrossRef]
- Taskinoglu, E.; Bellan, J. A posteriori study using a DNS database describing fluid disintegration and binary-species mixing under supercritical pressure: Heptane and nitrogen. J. Fluid Mech. 2010, 645, 211–254. [Google Scholar] [CrossRef]
- Sierra-Pallares, J.; Parra-Santos, M.T.; García-Serna, J.; Castro, F.; Cocero, M.J. Numerical analysis of high-pressure fluid jets: Application to RTD prediction in supercritical reactors. J. Supercrit. Fluid 2009, 49, 249–255. [Google Scholar] [CrossRef]
- Schmitt, T.; Selle, L.; Ruiz, A.; Cuenot, B. Large-eddy simulation of supercritical-pressure round jets. AIAA J. 2010, 48, 2133–2144. [Google Scholar] [CrossRef]
- Müller, H.; Niedermeier, C.A.; Matheis, J.; Pfitzner, M.; Hickel, S. Large-eddy simulation of nitrogen injection at trans- and supercritical conditions. Phys. Fluids 2016, 28, 015102. [Google Scholar] [CrossRef]
- Selle, L.C.; Okong’o, N.A.; Bellan, J.; Harstad, K.G. Modelling of subgrid-scale phenomena in supercritical transitional mixing layers: An a priori study. J. Fluid Mech. 2007, 593, 57–91. [Google Scholar] [CrossRef]
- Selle, L.; Ribert, G. Modeling requirements for large-eddy simulation of turbulent flows under supercritical thermodynamic conditions. In Proceedings of the CTR Summer Program, Stanford, CA, USA, 6 July–1 August 2008. [Google Scholar]
- Foster, J.; Miller, R.S. A priori analysis of subgrid mass diffusion vectors in high pressure turbulent hydrogen/oxygen reacting shear layer flames. Phys. Fluids 2012, 24, 075114. [Google Scholar] [CrossRef]
- Ruiz, A.M.; Lacaze, G.; Oefelein, J.C.; Mari, R.; Cuenot, B.; Selle, L.; Poinsot, T. Numerical benchmark for high-Reynolds-number supercritical flows with large density gradients. AIAA J. 2016, 54, 1445–1460. [Google Scholar] [CrossRef]
- Kawai, S. Direct numerical simulation of transcritical turbulent boundary layers at supercritical pressures with strong real fluid effects. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Ries, F.; Obando, P.; Schevchuck, I.; Janicka, J.; Sadiki, A. Numerical analysis of turbulent flow dynamics and heat transport in a round jet at supercritical conditions. Int. J. Heat Fluid Fl. 2017, 66, 172–184. [Google Scholar]
- Mayer, W.; Telaar, J.; Branam, R.; Schneider, G.; Hussong, J. Raman measurements of cryogenic injection at supercritical pressure. Heat Mass Transf. 2003, 39, 709–719. [Google Scholar] [CrossRef]
- van der Waals, J.D. Over de Continuiteit van den Gas-en Vloeistoftoestand. Ph.D. Thesis, University of Leiden, Leiden, The Netherlands, 1873. [Google Scholar]
- Peng, D.Y.; Robinson, D.P. A new two-constant equation of state. Ind. Eng. Chem. Fundamen. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Redlich, O.; Kwong, J.N.S. On the thermodynamics of solutions. V. An equation of state. Fugacities of gaseous solutions. Chem. Rev. 1949, 44, 233–244. [Google Scholar] [CrossRef] [PubMed]
- Soave, G. Equilibrium constants from a modified Redlich-Kwong equation of state. Chem. Eng. Sci. 1972, 27, 1197–1203. [Google Scholar] [CrossRef]
- Abudour, A.M.; Mohammad, S.A.; Robinson, R.L., Jr.; Gasem, K.A.M. Volume-translated Peng-Robinson equation of state for saturated and single-phase liquid densities. Fluid Phase Equilibr. 2012, 335, 74–87. [Google Scholar] [CrossRef]
- Burcat, A.; Ruscic, B. Third Millennium Ideal Gas and Condensed Phase Thermochemical Database for Combustion with Updates from Active Thermochemical Tables. Report No. TAE 960; 2005. Available online: http://atct.anl.gov/ruscic/reprints/Burcat%202005.pdf (accessed on 4 August 2017).
- Chung, T.H.; Ajlan, M.; Lee, L.L.; Starling, K.E. Generalized multiparameter correlation for nonpolar and polar fluid transport properties. Ind. Eng. Chem. Res. 1988, 27, 671–679. [Google Scholar] [CrossRef]
- Linstrom, P.J.; Mallard, W.G. NIST chemistry webbook. Available online: http://webbook.nist.gov/chemistry/fluid/ (accessed on 12 June 2017).
- Kock, F.; Herwig, H. Local entropy production in turbulent shear flows: A high-Reynolds number model with wall functions. Int. J. Heat Mass Tran. 2004, 47, 2205–2215. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 1985, 62, 40–65. [Google Scholar] [CrossRef]
- Patankar, S.; Spalding, D. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int. J. Heat Mass Tran. 1972, 15, 1787–1806. [Google Scholar] [CrossRef]
- Roe, P.L. Characteristic-based schemes for the euler equations. Ann. Rev. Fluid Mech. 1986, 18, 337–365. [Google Scholar] [CrossRef]
- Greenshields, C.J. OpenFOAM Programmer’s Guide Version 3.0.1. Available online: http://foam.sourceforge.net/docs/Guides-a4/ProgrammersGuide.pdf (accessed on 4 August 2017).
- Tavoularis, S.; Corrsin, S. Experiments in nearly homogenous turbulent shear flow with a uniform mean temperature gradient. Part 1. J. Fluid Mech. 1981, 104, 311–347. [Google Scholar] [CrossRef]
- Batchelor, G.K. Diffusion in a field of homogeneous turbulence. I. Eulerian analysis. Aust. J. Chem. 1949, 2, 437–450. [Google Scholar] [CrossRef]
- Daly, B.J.; Harlow, F.H. Transport equations in turbulence. Phys. Fluids 1970, 13, 2637–2649. [Google Scholar] [CrossRef]
- Younis, B.A.; Speziale, C.G.; Clark, T.T. A rational model for the turbulent scalar fluxes. Proc. Math. Phys. Eng. Sci. 2004, 461, 575–594. [Google Scholar] [CrossRef]
- Bogucki, D.; Domaradzki, J.A.; Yeung, P.K. Direct numerical simulations of passive scalars with Pr > 1 advected by turbulent flow. J. Fluid Mech. 1997, 343, 111–130. [Google Scholar] [CrossRef]
- Borgas, M.S.; Sawford, B.L.; Xu, S.; Donzis, D.A.; Yeung, P.K. High Schmidt number scalars in turbulence: Structure functions and Lagrangian theory. Phys. Fluids 2004, 16, 3888–3899. [Google Scholar] [CrossRef]
- Peng, S.H.; Davidson, L. On a subgrid-scale heat flux model for large eddy simulation of turbulent thermal flow. Int. J. Heat Mass Tran. 2002, 45, 1393–1405. [Google Scholar] [CrossRef]
- Wang, B.; Bergstrom, D.J. A dynamic nonlinear subgrid-scale stress model. Phys. Fluids 2005, 17, 035109. [Google Scholar] [CrossRef]
- Rasam, A.; Brethouwer, G.; Johansson, A.V. An explicit algebraic model for the subgrid-scale passive scalar flux. J. Fluid Mech. 2013, 721, 541–577. [Google Scholar] [CrossRef]
- Pantangi, P.; Huai, Y.; Sadiki, A. Mixing analysis and optimization in jet mixer systems by means of large eddy simulation. In Micro and Macro Mixing: Analysis, Simulation, and Numerical Calculation; Bockhorn, H., Mewes, D., Peukert, W., Warnecke, H.J., Eds.; Springer Verlag: Berlin, Germany, 2010. [Google Scholar]











| Property | Description | Value |
|---|---|---|
| injection velocity | m/s | |
| injection temperature | K | |
| chamber temperature | 298 K | |
| chamber pressure | MPa | |
| injection -number | 5300 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ries, F.; Janicka, J.; Sadiki, A. Thermal Transport and Entropy Production Mechanisms in a Turbulent Round Jet at Supercritical Thermodynamic Conditions. Entropy 2017, 19, 404. https://doi.org/10.3390/e19080404
Ries F, Janicka J, Sadiki A. Thermal Transport and Entropy Production Mechanisms in a Turbulent Round Jet at Supercritical Thermodynamic Conditions. Entropy. 2017; 19(8):404. https://doi.org/10.3390/e19080404
Chicago/Turabian StyleRies, Florian, Johannes Janicka, and Amsini Sadiki. 2017. "Thermal Transport and Entropy Production Mechanisms in a Turbulent Round Jet at Supercritical Thermodynamic Conditions" Entropy 19, no. 8: 404. https://doi.org/10.3390/e19080404
APA StyleRies, F., Janicka, J., & Sadiki, A. (2017). Thermal Transport and Entropy Production Mechanisms in a Turbulent Round Jet at Supercritical Thermodynamic Conditions. Entropy, 19(8), 404. https://doi.org/10.3390/e19080404