Irregularity and Variability Analysis of Airflow Recordings to Facilitate the Diagnosis of Paediatric Sleep Apnoea-Hypopnoea Syndrome
Abstract
:1. Introduction
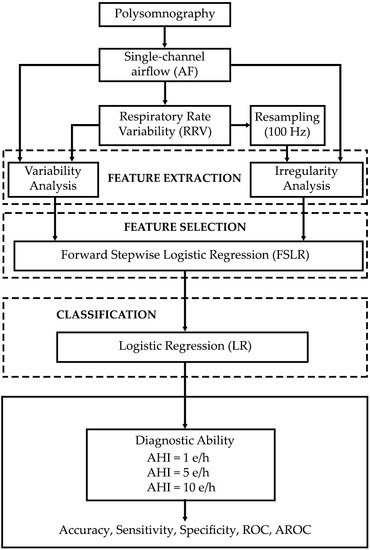
2. Materials and Methods
2.1. Subjects and Signals
2.2. Methods
2.2.1. Feature Extraction
2.2.2. Feature Selection
2.2.3. Classification
2.2.4. Statistical Analysis
3. Results
3.1. Training Group
3.1.1. Exploratory Analysis
3.1.2. Selected Features and Model Training
3.2. Test Group
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Patil, S.P.; Schneider, H.; Schwartz, A.R.; Smith, P.L. Adult obstructive apnea: Pathophysiology and diagnosis. Chest 2007, 132, 325–337. [Google Scholar] [CrossRef] [PubMed]
- Berry, R.B.; Budhiraja, R.; Gottlieb, D.J.; Gozal, D.; Iber, C.; Kapur, V.K.; Marcus, C.L.; Mehra, R.; Parthasarathy, S.; Quan, S.F.; et al. Rules for scoring respiratory events in sleep: Update of the 2007 AASM manual for the scoring of sleep and associated events. J. Clin. Sleep Med. 2012, 8, 597–619. [Google Scholar] [CrossRef] [PubMed]
- Kaditis, A.G.; Alonso-Alvarez, M.L.; Boudewyns, A.; Alexopoulos, E.I.; Ersu, R.; Joosten, K.; Larramona, H.; Miano, S.; Narang, I.; Trang, H.; et al. Obstructive sleep disordered breathing in 2–18 year-old children: Diagnosis and management. Eur. Respir. J. 2016, 47, 69–94. [Google Scholar] [CrossRef] [PubMed]
- Lipton, A.J.; Gozal, D. Treatment of obstructive sleep apnea in children: Do we really know how? Sleep Med. Rev. 2003, 7, 61–80. [Google Scholar] [CrossRef] [PubMed]
- Carroll, J.L.; Loughlin, G.M. Diagnostic criteria for obstructive sleep apnea syndrome in children. Pediatr. Pulmonol. 1992, 14, 71–74. [Google Scholar] [CrossRef] [PubMed]
- Marcus, C.L. Obstructive sleep apnea syndrome: Differences between children and adults. Sleep 2000, 23, 140–141. [Google Scholar]
- Spruyt, K. Pediatric Sleep-Disordered Breathing: Criteria and Spectrum of Disease. In Sleep Disordered Breathing in Children: A Comprehensive Clinical Guide to Evaluation and Treatment, 1st ed.; Kheirandish-Gozal, L., Gozal, D., Eds.; Humana Press: New York, NY, USA, 2012; pp. 245–260. [Google Scholar]
- Tan, H.L.; Gozal, D.; Ramirez, H.M.; Bandla, H.P.R.; Kheirandish-Gozal, L. Overnight polysomnography versus respiratory polygraphy in the diagnosis of pediatric obstructive sleep apnea. Sleep 2014, 37, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Alonso-Álvarez, M.L.; Canet, T.; Cubell-Alarco, M.; Estivill, E.; Fernández-Julián, E.; Gozal, D.; Jurado-Luque, M.J.; Lluch-Roselló, M.A.; Martínez-Pérez, F.; Merino-Andren, M.; et al. Consensus Document on Sleep Apnea-Hypopnea Syndrome in Children. Arch. Bronconeumol. 2011, 47, 2–18. [Google Scholar]
- Church, G.D. The Role of Polysomnography in Diagnosing and Treating Obstructive Sleep Apnea in Pediatric Patients. Curr. Probl. Pediatr. Adolesc. Health Care 2012, 42, 2–25. [Google Scholar] [CrossRef] [PubMed]
- Epstein, L.J.; Kristo, D.; Strollo, P.J., Jr.; Friedman, N.; Malhotra, A.; Patil, S.P.; Ramar, K.; Rogers, R.; Schwab, R.J.; Weaver, E.M.; et al. Clinical guideline for the evaluation, management and long-term care of obstructive sleep apnea in adults. Adult obstructive sleep apnea Task Force of the American Academy of Sleep Medicine. J. Clin. Sleep Med. 2009, 5, 263–276. [Google Scholar] [PubMed]
- Marcus, C.L.; Brooks, L.J.; Ward, S.D.; Draper, K.A.; Gozal, D.; Halbower, A.C.; Jones, J.; Lehmann, C.; Schechter, M.S.; Sheldon, S.; et al. Diagnosis and management of childhood obstructive sleep apnea syndrome. Pediatrics 2012, 130, 714–755. [Google Scholar] [CrossRef] [PubMed]
- Ryan, P.J.; Hilton, M.F.; Boldy, D.A.; Evans, A.; Bradbury, S.; Sapiano, S.; Prowse, K.; Cayton, R.M. Validation of British Thoracic Society guidelines for the diagnosis of the sleep apnoea/hypopnoea syndrome: Can polysomnography be avoided? Thorax 1995, 50, 972–975. [Google Scholar] [CrossRef] [PubMed]
- Katz, E.S.; Mitchell, R.B.; D’Ambrosio, C.M. Obstructive Sleep Apnea in Infants. Am. J. Respir. Crit. Care Med. 2012, 185, 805–816. [Google Scholar] [CrossRef]
- Velasco-Suarez, C.T.; Figueroa-Turienzo, J.M.; Len, F.; Mansilla, E. Pulse oximetry recording in children with adenotonsillar hypertrophy: Usefulness in the diagnostic of obstructive sleep apnea syndrome. Arch. Argent Pediatr. 2013, 111, 196–201. [Google Scholar] [CrossRef] [PubMed]
- Shouldice, R.B.; O’Brien, L.M.; O’Brien, C.; Chazal, P.; Gozal, D.; Heneghan, C. Detection of Obstructive Sleep Apnea in Pediatric Subjects using Surface Lead Electrocardiogram Features. Sleep 2004, 27, 784–792. [Google Scholar] [CrossRef] [PubMed]
- Gil, E.; Mendez, M.; Vergara, J.M.; Cerutti, S.; Bianchi, A.M.; Laguna, P. Discrimination of Sleep-Apnea-Related Decreases in the Amplitude Fluctuations of PPG Signal in Children by HRV Analysis. IEEE Trans. Biomed. Eng. 2009, 56, 1005–1014. [Google Scholar] [CrossRef] [PubMed]
- Lázaro, J.; Gil, E.; Vergara, J.M.; Laguna, P. Pulse rate variability analysis for discrimination of sleep-apnea-related decreases in the amplitude fluctuations of pulse photoplethysmographic signal in children. IEEE J. Biomed. Health Inform. 2014, 18, 240–246. [Google Scholar] [CrossRef]
- Gil, E.; Bailón, R.; Vergara, J.M.; Laguna, P. PTT Variability for Discrimination of Sleep Apnea Related Decreases in the Amplitude Fluctuations of PPG Signal in Children. IEEE Trans. Biomed. Eng. 2010, 57, 1079–1088. [Google Scholar] [CrossRef] [PubMed]
- Garde, A.; Dehkordi, P.; Karlen, W.; Wensley, D.; Ansermino, J.M.; Dumont, G.A. Development of a Screening Tool for Sleep Disordered Breathing in Children Using the Phone OximeterTM. PLoS ONE 2014, 9, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Dehkordi, P.; Garde, A.; Karlen, W.; Petersen, C.L.; Wensley, D.; Dumont, G.A.; Ansermino, J.M. Evaluation of cardiac modulation in children in response to apnea/hypopnea using the Phone OximeterTM. Physiol. Meas. 2016, 37, 187–202. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez-Tobal, G.C.; Alonso-Álvarez, M.L.; Álvarez, D.; del Campo, F.; Terán-Santos, J.; Hornero, R. Diagnosis of pediatric obstructive sleep apnea: Preliminary findings using automatic analysis of airflow and oximetry recordings obtained at patients’ home. Biomed. Signal Process. Control 2015, 18, 401–407. [Google Scholar] [CrossRef]
- Sahadan, D.Z.; Davey, M.J.; Horne, R.S.C.; Nixon, G.M. Improving detection of obstructive sleep apnoea by overnight oximetry in children using pulse rate parameters. Sleep Breath. 2015, 19, 1409–1414. [Google Scholar] [CrossRef] [PubMed]
- Tsai, C.M.; Kang, C.H.; Su, M.C.; Lin, H.C.; Huang, E.Y.; Chen, C.C.; Hung, J.C.; Niu, C.K.; Liao, D.L.; Yu, H.R. Usefulness of desaturation index for the assessment of obstructive sleep apnea syndrome in children. Int. J. Pediatr. Otorhinolaryngol. 2013, 77, 1286–1290. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez-Tobal, G.C.; Hornero, R.; Álvarez, D.; Marcos, J.V.; del Campo, F. Linear and nonlinear analysis of airflow recordings to help in sleep apnoea–hypopnoea syndrome diagnosis. Physiol. Meas. 2012, 33, 1261–1275. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Shin, H.B.; Jeong, D.U.; Park, K.S. Detection of apnoeic events from single channel nasal airflow using 2nd derivative method. Comput. Methods Programs Biomed. 2008, 98, 199–207. [Google Scholar] [CrossRef]
- Cysarz, D.; Zerm, R.; Bettermann, H.; Frühwirth, M.; Moser, M.; Kröz, M. Comparison of respiratory rates derived from heart rate variability, ECG amplitude, and nasal/oral airflow. Ann. Biomed. Eng. 2008, 36, 2085–2094. [Google Scholar] [CrossRef] [PubMed]
- Poza, J.; Hornero, R.; Abásolo, D.; Fernández, A.; García, M. Extraction of spectral based measures from MEG background oscillations in Alzheimer’s disease. Med. Eng. Phys. 2007, 29, 1073–1083. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chua, K.C.; Chandran, V.; Acharya, U.R.; Min, L.C. Cardiac state diagnosis using higher order spectra of heart rate variability. J. Med. Eng. Technol. 2008, 32, 145–155. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez-Tobal, G.C.; Álvarez, D.; Gómez-Pilar, J.; del Campo, F.; Hornero, R. Assessment of Time and Frequency Domain Entropies to Detect Sleep Apnoea in Heart Rate Variability Recordings from Men and Women. Entropy 2015, 17, 123–141. [Google Scholar] [CrossRef]
- Atri, R.; Mohebbi, M. Obstructive sleep apnea detection using spectrum and bispectrum analysis of single-lead ECG signal. Physiol. Meas. 2015, 36, 1963–1980. [Google Scholar] [CrossRef] [PubMed]
- Abásolo, D.; Hornero, R.; Gómez, C.; García, M.; López, M. Analysis of EEG background activity in Alzheimer’s disease patients with Lempel–Ziv complexity and central tendency measure. Med. Eng. Phys. 2006, 28, 315–322. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cohen, M.E.; Hudson, D.L.; Deedwania, P.C. Applying continuous chaotic modeling to cardiac signals. IEEE Eng. Med. Biol. Mag. 1996, 15, 97–102. [Google Scholar] [CrossRef]
- Álvarez, D.; Hornero, R.; García, M.; del Campo, F.; Zamarrón, C. Improving diagnostic ability of blood oxygen saturation from overnight pulse oximetry in obstructive sleep apnea detection by means of central tendency measure. Artif. Intell. Med. 2007, 41, 13–24. [Google Scholar] [CrossRef] [PubMed]
- Hosmer, D.W.; Lemeshow, S. Applied Logistic Regression; John Wiley & Sons: London, UK, 2000. [Google Scholar]
- Varady, P.; Micsik, T.; Benedek, S.; Benyo, Z. A novel method for the detection of apnea and hypopnea events in respiration signals. IEEE Trans. Biomed. Eng. 2002, 49, 936–942. [Google Scholar] [CrossRef] [PubMed]
- Welch, P.D. The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on time Averaging Over Short, Modified Periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef]
- Fleming, S.; Thompson, M.; Stevens, R.; Heneghan, C.; Plüddemann, A.; Maconochie, I.; Tarassenko, L.; Mant, D. Normal ranges of heart rateand respiratory rate in children from birth to 18 years of age: A systematic review of observational studies. Lancet 2011, 377, 1011–1018. [Google Scholar] [CrossRef]
- Gutiérrez-Tobal, G.C.; Álvarez, D.; del Campo, F.; Hornero, R. Utility of AdaBoost to Detect Sleep Apnea-Hypopnea Syndrome From Single-Channel Airflow. IEEE Trans. Biomed. Eng. 2016, 63, 636–646. [Google Scholar] [CrossRef] [PubMed]
- Álvarez, D.; Hornero, R.; Marcos, J.V.; del Campo, F. Multivariate analysis of blood oxygen saturation recordings in obstructive sleep apnea diagnosis. IEEE Trans. Biomed. Eng. 2010, 57, 2816–2824. [Google Scholar] [CrossRef] [PubMed]
- Sutter, J.M.; Kalivas, J.H. Comparison of forward selection, backward elimination and generalized simulated annealing for variable selection. Microchem. J. 1993, 47, 60–66. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Flemons, W.W.; Littner, M.R. Measuring agreement between diagnostic devices. Chest 2003, 124, 1535–1542. [Google Scholar] [CrossRef] [PubMed]
- Zweig, M.H.; Campbell, G. Receiver-operating characteristic (ROC) plots: A fundamental evaluation tool in clinical medicine. Clin. Chem. 1993, 39, 561–577. [Google Scholar] [PubMed]
- Bishop, C.M. Pattern Recognition and Machine Learning, 1st ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Kaditis, A.; Kheirandish-Gozal, L.; Gozal, D. Pediatric OSAS: Oximetry can provide answers when polysomnography is not available. Sleep Med. Rev. 2016, 27, 96–105. [Google Scholar] [CrossRef] [PubMed]
- Hunter, S.J.; Gozal, D.; Smith, D.L.; Philby, M.F.; Kaylegian, J.; Kheirandish-Gozal, L. Effect of Sleep-disordered Breathing Severity on Cognitive Performance Measures in a Large Community Cohort of Young School-aged Children. Am. J. Respir. Crit. Care Med. 2016, 194, 739–747. [Google Scholar] [CrossRef] [PubMed]






| Characteristics | All | Training Group | Test Group |
|---|---|---|---|
| Subjects (n) | 501 | 250 | 251 |
| Age (years) | 6 [3, 9] | 6 [4, 8] | 6 [3, 9] |
| Males (n) | 314 (62.67%) | 160 (64%) | 154 (61.35%) |
| BMI (kg/m2) | 17.81 [15.75, 22.21] | 17.39 [15.57, 21.97] | 18.14 [16.11, 22.44] |
| AHI (e/h) | 3.2 [0.95, 8.08] | 2.69 [0.77, 7.28] | 3.53 [1.37, 9.06] |
| AHI ≥ 1 (e/h) | 367 (73.25%) | 170 (68%) | 197 (78.49%) |
| AHI ≥ 5 (e/h) | 180 (35.93%) | 83 (33.2%) | 97 (38.65%) |
| AHI ≥ 10 (e/h) | 104 (20.76%) | 48 (19.2%) | 56 (22.31%) |
| Model | Se (%) | Sp (%) | Acc (%) |
|---|---|---|---|
| LR1 | 60.5 | 58.6 | 60.0 |
| LR5 | 65.0 | 80.6 | 76.0 |
| LR10 | 83.3 | 79.0 | 80.0 |
| Studies | Subjects (n) | Signal | AHI (e/h) | Methods (Analysis/Selection/Classifier) | Se (%) | Sp (%) | Acc (%) |
|---|---|---|---|---|---|---|---|
| Shouldice et al. [16] (2004) | 50 | ECG | 1 | Temporal and spectral analysis/–/QDA | 85.7 | 81.8 | 84 |
| Gil et al. (2009) [17] | 21 | PPG | 5 | Spectral analysis of HRV and DAP events detection/Wrapper methodology/LDA | 87.5 | 71.4 | 80 |
| Lázaro et al. [18] (2014) | 21 | PPG | 5 | Spectral analysis of PRV and DAP events detection/Wrapper methodology/LDA | 100 | 71.4 | 86.7 |
| Gil et al. (2010) [19] | 21 | PPG | 5 | Analysis of PTTV/Wrapper methodology/LDA | 75 | 85.7 | 80 |
| Garde et al. [20] (2014) | 146 | SpO2 PRV | 5 | Temporal and spectral analysis/Selection algorithm optimizing the AROC/LDA | 88.4 | 83.6 | 84.9 |
| Dehkordi et al. [21] (2016) | 146 | PPG | 5 | Temporal and spectral analysis/LASSO/LASSO | 76 | 68 | 71 |
| Sahadan et al. [23] (2015) | 93 | PR | 1 | Automatic calculation and analysis of PR parameters/–/–/ | 18 | 97 | 49.5 * |
| Velasco-Suarez et al. [15] (2013) | 167 | SpO2 | 1 | Quantification of clusters of desaturations/–/–/ | 86.6 | 98.9 | 93.4 * |
| Gutiérrez-Tobal et al. [22] (2015) | 50 | AF SpO2 | 3 | Spectral features and oxygen desaturation index of 3% (ODI3)/FSLR/LR | 85.9 | 87.4 | 86.3 |
| Tsai et al. [24] (2013) | 148 | SpO2 | 1 | Oxygen desaturation index of 4% (ODI4) /–/–/ | 77.7 | 88.9 | 79 * |
| 5 | 83.8 | 86.5 | 85.1 * | ||||
| 10 | 89.1 | 86 | 87.1 * | ||||
| Tan et al. [8] (2014) | 100 | ECG | 1 | Comparison of the AHI obtained from PSG with the AHI directly estimated of respiratory polygraphic (RP)/–/–/ | 82.5 | 90 | 86 * |
| AF SpO2 | 5 | 62.5 | 100 | 85 * | |||
| RIP | 10 | 65 * | 100 * | 93 * | |||
| Our proposal | 501 | AF | 1 | SE and CTM/FSLR/LR | 60.5 | 58.6 | 60 |
| 5 | 65 | 80.6 | 76 | ||||
| 10 | 83.3 | 79 | 80 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barroso-García, V.; Gutiérrez-Tobal, G.C.; Kheirandish-Gozal, L.; Álvarez, D.; Vaquerizo-Villar, F.; Crespo, A.; Del Campo, F.; Gozal, D.; Hornero, R. Irregularity and Variability Analysis of Airflow Recordings to Facilitate the Diagnosis of Paediatric Sleep Apnoea-Hypopnoea Syndrome. Entropy 2017, 19, 447. https://doi.org/10.3390/e19090447
Barroso-García V, Gutiérrez-Tobal GC, Kheirandish-Gozal L, Álvarez D, Vaquerizo-Villar F, Crespo A, Del Campo F, Gozal D, Hornero R. Irregularity and Variability Analysis of Airflow Recordings to Facilitate the Diagnosis of Paediatric Sleep Apnoea-Hypopnoea Syndrome. Entropy. 2017; 19(9):447. https://doi.org/10.3390/e19090447
Chicago/Turabian StyleBarroso-García, Verónica, Gonzalo César Gutiérrez-Tobal, Leila Kheirandish-Gozal, Daniel Álvarez, Fernando Vaquerizo-Villar, Andrea Crespo, Félix Del Campo, David Gozal, and Roberto Hornero. 2017. "Irregularity and Variability Analysis of Airflow Recordings to Facilitate the Diagnosis of Paediatric Sleep Apnoea-Hypopnoea Syndrome" Entropy 19, no. 9: 447. https://doi.org/10.3390/e19090447
APA StyleBarroso-García, V., Gutiérrez-Tobal, G. C., Kheirandish-Gozal, L., Álvarez, D., Vaquerizo-Villar, F., Crespo, A., Del Campo, F., Gozal, D., & Hornero, R. (2017). Irregularity and Variability Analysis of Airflow Recordings to Facilitate the Diagnosis of Paediatric Sleep Apnoea-Hypopnoea Syndrome. Entropy, 19(9), 447. https://doi.org/10.3390/e19090447