1. Introduction
Leakage is a gradual escape of a current from a transportation channel or a container. The current can be an electric charge, magnetic flux, information, heat or fluid flow, etc. The management and control of these leakages are important topics. Among various leakages, fluid leak in a pipe is one of the simplest forms, widely existing in biology, process industries, and engineering.
Leakage plays different roles, depending on the application. A minimized leakage rate is required in industries involving, for instance, water/oil/gas processing, or energy recovery/storage. In the chemical process industry, leakage of flammable, radioactive, or explosive fluids is dangerous and even disastrous. On another hand, leakage may play a positive role in biological transportation, like drug delivery, capillary exchange, or cellular membrane filtration.
Towards a better process control of the leakage, an important strategy is to design a reasonable leakage criterion. Usually, leakage through cracks at a microscale or nanoscale is invisible or difficult to identify, even though various technical efforts like non-destructive evaluation or contact mechanics analysis [
1]. Therefore, most existing leakage criteria are commonly empirical and not clearly defined. In addition, traditional leakage criterion are hardly valid in multiscale leakage evaluation.
Recently, the virtual entropy generation (VEG) method has been used in the design of process evaluation criterion for the heat exchange process [
2,
3,
4]. In this method, VEG was defined as [
3] the entropy generation difference of a real-life measurable process and an ideal irreversible process. Under the constraint of a non-negative entropy generation measurement for a real-life thermodynamic process, corresponding evaluation criteria can be obtained. Compared to traditional evaluation methods [
5], the VEG method always provides a physically “meaningful” solution [
2,
3,
4].
From the thermodynamic perspective, leakage happens in a process such as heat transfer [
6], fluid flow, electric power transmission [
7], or information transfer [
8]. Defining a leakage criterion equals defining the process criterion. Evaluation of a leakage process by the VEG method has not been conducted.
In the present research, a leakage evaluation criterion in a single pipe was derived using the VEG method analytically. The leakage induced virtual entropy generation was controlled by the flow process entropy generation. We used published experimental data and numerical simulations to show how to use this parameter in the evaluation and control of leakage. The present research method would provide suggestive criteria for leakage control and leakage detection systems.
3. Analytical Model
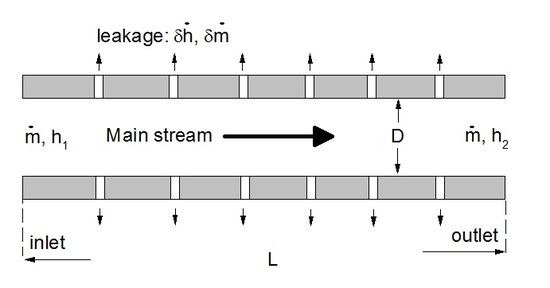
Fluid leakage in a pipe flow is one of the most common forms of leakage caused by cracks in the wall. Cracks on the scale of micron or sub-micron in a pipe are mainly caused by corrosion, operation outside design limit, or damage. The crack commonly exists in the form of multiple paths or porous structures [
9]. Leaking through a crack is most often difficult to detect and hard to predict.
For a pipe flow without leakage, the entropy generation of an “ideal irreversible” process is [
10]
where
is the mass flow rate at the inlet of the pipe,
is the entropy at the outlet, and
is the entropy at the inlet.
In an experiment, the value of entropy generation for a leaky pipe flow is determined by the entropy difference between the outlet and inlet. For a general leaky pipe [
11], by assuming a decreased mass flow rate at the outlet (i.e.,
,
), the indirect measurement value of entropy generation in this leaky pipe can be expressed as
Further, Equation (3) can be decomposed as
In Equation (4), the first term on the right-hand side expresses the irreversibility of the flow through a real pipe, while the second term is the VEG caused by leaking.
An “ideal reversible” pipe transportation process has a positive entropy generation due to irreversibility. However, the condition of the second-law of thermodynamics may be too harsh in some cases. For example, it is not easy to isolate a 10-km-long pipeline transportation process in a real engineering case due to multiple leakages. Also, it is not possible to identify all leaking points in this real process. The “measured” entropy generation may return “negative” or invalid.
From the virtual entropy generation perspective, the invalid “measured entropy generation” is an indicator of unreliability in a real-life process. It points out a direction we need go against. For the case of a single pipe leakage, ‘invalid entropy generation’ is caused by undetected leakage. To prevent the over-leakage, the virtual entropy generation criterion, , may help control and evaluate leakage.
Due to the mass leakage (), the irreversibility measured for a real process may decrease, even leading to a negative value in Equation (3). The decrease in entropy generation will not happen in an isolated system or an ideal invertible process without leakage. However, for a leaky pipe with multiple outputs, it is not possible to take all the leaking conditions into consideration. The model we are proposing in this paper exists in many real-life conditions such as in a long-distance gas/oil transportation or a diffusion based capillary exchange, where multiple leaky sites could arise beyond normal control. To prevent a non-physical measurement, a VEG criterion should be determined to prevent a serious leaking situation.
According to the first law of thermodynamics, the enthalpy for a single-phase flow can be written as
where
is the enthalpy change. According to the first law of thermodynamics, the adiabatic flow condition happens in a rapid flow condition when the flow is much faster than the leaking condition. Usually, the mass leakage flow process is a rapid process. It is much faster than the heat transfer process. Thus, we can use the adiabatic approximation, with d
h = 0;
T is the temperature assumed as constant for the adiabatic process;
is the variance of entropy generation;
is the specific volume of the fluid of mass density
; and
is the pressure change along the pipe. Thus, for an adiabatic process, Equation (5) reduces to
The leaking process is characterized by a mass flow rate
and a pressure drop from
to
. Integrating Equation (6) further gives
Dividing the constant term (
) on both sides of Equation (7), a relation can be obtained in the form of
Here, Δ
P is the pressure drop across the inlet and outlet. The pressure at outlet [
12] changes due to leakage (
) and friction (
), i.e.,
. The friction induced pressure drop is described by Darcy–Weisbach equation:
. Here,
f is the friction factor,
L is the length of the main channel,
D is the diameter of a pipe, and
V is the bulk velocity of the fluid. For an ideal compressible gas,
,
R is the gas constant. By dividing
R on both sides of Equation (7), Equation (8) is still valid. Thus Equation (8) is valid for both incompressible and compressible fluids.
For cases with a small mass leakage rate,
the mass leakage rate is bounded by the operation condition of the ideal process in the non-dimensional form of
The mass leakage criterion defined here is a variable criterion: a high mass leakage rate is acceptable for a long-distance transportation with a high pressure drop rate. For a short distance, or transportation of a fluid with low viscosity through a smooth surface pipe, the VEG criterion in Equation (9) suggests a small mass leakage rate (). For long-distance transportation of a fluid with high viscosity through a rough surface pipe, a relatively high mass leakage rate is acceptable. This provides a criterion to control the cross-channel-wall mass leakage rate by the pressure drop along the pipe. The inlet pressure is commonly determined by a designed transportation requirement, or is constant.
The velocity of fluid after the leakage site decreases. Thus, the pressure drop across the leakage becomes lower. The measurement of pressure difference from the inlet to the outlet, , becomes smaller. Consequently, the outlet entropy generation flowrate at the outlet in Equation (3) decreases fast at a high leakage rate.
Here, we define a critical mass leakage rate,
. By inserting the critical leakage rate back in the expression of experimental entropy generation in Equation (4), we can obtain
Thus, the entropy generation measured is already negative at the critical mass leakage rate. As we noticed that Equations (1)–(10) have no scale limit. However, for a leakage problem, cracks are commonly at microscale or nanoscale.
In
Figure 2a, the relation among
,
, and
is plotted. As can be seen, when
, the measured entropy generation is negative and increases linearly with
and
. Besides, we defined a non-dimensional form of entropy generation in
Figure 2b by dividing the entropy generation measured by the undetectable virtual entropy generation
. As can be seen on the right side of Equation (4), the non-dimensional form of entropy generation is the ratio of the first term and the second term. This ratio in the non-dimensional form provides a method to decrease the proportion of virtual entropy generation by increasing the pressure loss in the transportation at a constant inlet pressure condition.
4. Concept Validation by Computational Fluid Dynamics
In this part, Computational Fluid Dynamic (CFD) simulations were conducted to show the existence of invalid entropy generation measurement in a leaky pipe. The numerical model was built based on the configuration in
Figure 3. The main difference is that we focused on a single undetectable crack in the middle of the main channel. The main channel was set as 2 mm in height. The crack in the wall was modeled as a microchannel with three different widths of 50, 100, or 200 μm in height. The liquid viscosity is set as
and the gas viscosity was set as
. Both liquid and gas are in laminar flow.
In the simulation, the pressure drop rate (α), which is the x-axis, was achieved by setting the pressure at the main channel inlet and outlet. The inlet boundary condition was defined as a stagnation inlet boundary (total pressure), and the outlet boundary condition was defined as a pressure outlet boundary (static pressure). The ambient pressure is assumed as 0-gauge. The pressure drop rate (α) steps from 1% to the value when the mass leakage rate (β) disobeys Equation (9). The inlet pressure of the main channel was set as a constant of 10 kPa for static pressure. The mass loss percentage (β), which is the y-axis, was collected from simulation results by solving the Navier–Stokes equation in the Standard CFD solver Ansys Fluent.
By setting the pressure difference, the mass flow rate of two outlets (outlet 1 and leakage outlet in the middle of the main channel) changes accordingly. Due to the leakage, the velocity after the crack decreased. As can be seen in
Figure 4b, more mass flow was leaked at a higher velocity through a wider crack at the same inlet pressure and pressure drop. Pressure drop rate and mass leakage rate relation for three crack widths (50, 100, and 200 μm) were summarized in
Figure 5a. With the increase of
, both
and
increase. However, the mass leakage rate,
decreases linearly with the increase of
. Besides, we conducted a comparison study between incompressible and compressible (ideal gas) model in
Figure 5b. As can be seen, the compressibility of gas slightly reduces the mass leakage rate in a high inlet pressure (
Pin = 10 kPa) and low pressure drop rate (
) flow case. The influence is caused by the high velocity in the leakage channel. In this case, although the velocity in the main channel is low (Ma ~ 0.01), the velocity in the leakage channel can reach up to Ma ~ 0.3. Further research on the high Mach number and compressibility influence can be seen in [
13].