Entropy of Simulated Liquids Using Multiscale Cell Correlation
Abstract
:1. Introduction
2. Theory
2.1. Entropy Decomposition
2.2. Molecular Vibrational Entropy
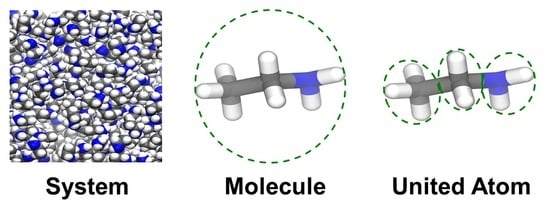
2.3. United-Atom Vibrational Entropy
2.4. Molecular Topographical Entropy
2.5. United-Atom Topographical Entropy
2.6. Molecular Dynamics Simulations
3. Results
3.1. Entropy Values
3.2. Entropy Components
3.3. Covariance Matrices and Coordination and Dihedral Distributions
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MCC | Multiscale Cell Correlation |
| 2PT | 2-Phase Thermodynamics |
| GAFF | Generalized AMBER Force Field |
| OPLS | Optimized Potentials for Liquid Simulations |
| TraPPE | Transferable Potentials for Phase Equilibria |
References
- Peter, C.; Oostenbrink, C.; van Dorp, A.; van Gunsteren, W.F. Estimating entropies from molecular dynamics simulations. J. Chem. Phys. 2004, 120, 2652–2661. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.X.; Gilson, M.K. Theory of Free Energy and Entropy in Noncovalent Binding. Chem. Rev. 2009, 109, 4092–4107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van Speybroeck, V.; Gani, R.; Meier, R.J. The calculation of thermodynamic properties of molecules. Chem. Soc. Rev. 2010, 39, 1764–1779. [Google Scholar] [CrossRef] [PubMed]
- Polyansky, A.A.; Zubac, R.; Zagrovic, B. Estimation of Conformational Entropy in Protein-Ligand Interactions: A Computational Perspective. In Computational Drug Discovery and Design; Baron, R., Ed.; Springer: Berlin, Germany, 2012; Volume 819, pp. 327–353. [Google Scholar]
- Baron, R.; McCammon, J.A. Molecular Recognition and Ligand Association. Ann. Rev. Phys. Chem. 2013, 64, 151–175. [Google Scholar] [CrossRef] [PubMed]
- Suárez, D.; Diaz, N. Direct methods for computing single-molecule entropies from molecular simulations. Rev. Comput. Sci. 2015, 5, 1–26. [Google Scholar] [CrossRef]
- Kassem, S.; Ahmed, M.; El-Sheikh, S.; Barakat, K.H. Entropy in bimolecular simulations: A comprehensive review of atomic fluctuations-based methods. J. Mol. Graph. Model. 2015, 62, 105–117. [Google Scholar] [CrossRef] [PubMed]
- Butler, K.T.; Walsh, A.; Cheetham, A.K.; Kieslich, G. Organised chaos: Entropy in hybrid inorganic-organic systems and other materials. Chem. Sci. 2016, 7, 6316–6324. [Google Scholar] [CrossRef] [PubMed]
- Chong, S.H.; Chatterjee, P.; Ham, S. Computer Simulations of Intrinsically Disordered Proteins. Ann. Rev. Phys. Chem. 2017, 68, 117–134. [Google Scholar] [CrossRef] [PubMed]
- Huggins, D.J.; Biggin, P.C.; Damgen, M.A.; Essex, J.W.; Harris, S.A.; Henchman, R.H.; Khalid, S.; Kuzmanic, A.; Laughton, C.A.; Michel, J.; et al. Biomolecular simulations: From dynamics and mechanisms to computational assays of biological activity. WIREs Comput. Mol. Sci. 2019, 9, e1393. [Google Scholar] [CrossRef]
- Edholm, O.; Berendsen, H.J.C. Entropy estimation from simulations of non-diffusive systems. Mol. Phys. 1984, 51, 1011–1028. [Google Scholar] [CrossRef]
- Wallace, D.C. On the role of density-fluctuations in the entropy of a fluid. J. Chem. Phys. 1987, 87, 2282–2284. [Google Scholar] [CrossRef]
- Baranyai, A.; Evans, D.J. Direct entropy calculation from computer-simulation of liquids. Phys. Rev. A 1989, 40, 3817–3822. [Google Scholar] [CrossRef] [PubMed]
- Lazaridis, T.; Karplus, M. Orientational correlations and entropy in liquid water. J. Chem. Phys. 1996, 105, 4294–4316. [Google Scholar] [CrossRef]
- Killian, B.J.; Kravitz, J.Y.; Gilson, M.K. Extraction of configurational entropy from molecular simulations via an expansion approximation. J. Chem. Phys. 2007, 127, 024107. [Google Scholar] [CrossRef] [PubMed]
- Hnizdo, V.; Tan, J.; Killian, B.J.; Gilson, M.K. Efficient calculation of configurational entropy from molecular simulations by combining the mutual-information expansion and nearest-neighbor methods. J. Comput. Chem. 2008, 29, 1605–1614. [Google Scholar] [CrossRef] [Green Version]
- King, B.M.; Silver, N.W.; Tidor, B. Efficient Calculation of Molecular Configurational Entropies Using an Information Theoretic Approximation. J. Phys. Chem. B 2012, 116, 2891–2904. [Google Scholar] [CrossRef] [Green Version]
- Suárez, E.; Suárez, D. Multibody local approximation: Application to conformational entropy calculations on biomolecules. J. Chem. Phys. 2012, 137, 084115. [Google Scholar] [CrossRef]
- Goethe, M.; Gleixner, J.; Fita, I.; Rubi, J.M. Prediction of Protein Configurational Entropy (Popcoen). J. Chem. Theory Comput. 2018, 14, 1811–1819. [Google Scholar] [CrossRef]
- Goethe, M.; Fita, I.; Rubi, J.M. Testing the mutual information expansion of entropy with multivariate Gaussian distributions. J. Chem. Phys. 2017, 147, 224102. [Google Scholar] [CrossRef] [Green Version]
- Suárez, E.; Diaz, N.; Suárez, D. Entropy Calculations of Single Molecules by Combining the Rigid-Rotor and Harmonic-Oscillator Approximations with Conformational Entropy Estimations from Molecular Dynamics Simulations. J. Chem. Theory Comput. 2011, 7, 2638–2653. [Google Scholar] [CrossRef]
- Hnizdo, V.; Darian, E.; Fedorowicz, A.; Demchuk, E.; Li, S.; Singh, H. Nearest-neighbor nonparametric method for estimating the configurational entropy of complex molecules. J. Comput. Chem. 2007, 28, 655–668. [Google Scholar] [CrossRef] [PubMed]
- Hensen, U.; Lange, O.F.; Grubmüller, H. Estimating Absolute Configurational Entropies of Macromolecules: The Minimally Coupled Subspace Approach. PLoS ONE 2010, 5, e9179. [Google Scholar] [CrossRef] [PubMed]
- Huggins, D.J. Estimating Translational and Orientational Entropies Using the k-Nearest Neighbors Algorithm. J. Chem. Theory Comput. 2014, 10, 3617–3625. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karplus, M.; Kushick, J.N. Methods for Estimating the Configuration Entropy of Macromolecules. J. Am. Chem. Soc. 1981, 14, 325–332. [Google Scholar]
- Schlitter, J. Estimation of absolute and relative entropies of macromolecules using the covariance-matrix. Chem. Phys. Lett. 1993, 215, 617–621. [Google Scholar] [CrossRef]
- Andricioaei, I.; Karplus, M. On the calculation of entropy from covariance matrices of the atomic fluctuations. J. Chem. Phys. 2001, 115, 6289–6292. [Google Scholar] [CrossRef]
- Chang, C.E.; Chen, W.; Gilson, M.K. Evaluating the accuracy of the quasiharmonic approximation. J. Chem. Theory. Comput. 2005, 1, 1017–1028. [Google Scholar] [CrossRef]
- Reinhard, F.; Grubmüller, H. Estimation of absolute solvent and solvation shell entropies via permutation reduction. J. Chem. Phys. 2007, 126, 014102. [Google Scholar] [CrossRef]
- Dinola, A.; Berendsen, H.J.C.; Edholm, O. Free-energy determination of polypeptide conformations generated by molecular-dynamics. Macromolecules 1984, 17, 2044–2050. [Google Scholar] [CrossRef]
- Hikiri, S.; Yoshidome, T.; Ikeguchi, M. Computational Methods for Configurational Entropy Using Internal and Cartesian Coordinates. J. Chem. Theory Comput. 2016, 12, 5990–6000. [Google Scholar] [CrossRef] [Green Version]
- Gyimesi, G.; Zavodszky, P.; Szilagyi, A. Calculation of Configurational Entropy Differences from Conformational Ensembles Using Gaussian Mixtures. J. Chem. Theory Comput. 2017, 13, 29–41. [Google Scholar] [CrossRef]
- Lin, S.T.; Blanco, M.; Goddard, W.A. The two-phase model for calculating thermodynamic properties of liquids from molecular dynamics: Validation for the phase diagram of Lennard-Jones fluids. J. Chem. Phys. 2003, 119, 11792–11805. [Google Scholar] [CrossRef] [Green Version]
- Henchman, R.H. Partition function for a simple liquid using cell theory parametrized by computer simulation. J. Chem. Phys. 2003, 119, 400–406. [Google Scholar] [CrossRef]
- Henchman, R.H. Free energy of liquid water from a computer simulation via cell theory. J. Chem. Phys. 2007, 126, 064504. [Google Scholar] [CrossRef]
- Klefas-Stennett, M.; Henchman, R.H. Classical and quantum Gibbs free energies and phase behavior of water using simulation and cell theory. J. Phys. Chem. B 2008, 112, 3769–3776. [Google Scholar] [CrossRef] [PubMed]
- Henchman, R.H.; Irudayam, S.J. Topological hydrogen-bond definition to characterize the structure and dynamics of liquid water. J. Phys. Chem. B 2010, 114, 16792–16810. [Google Scholar] [CrossRef] [PubMed]
- Green, J.A.; Irudayam, S.J.; Henchman, R.H. Molecular interpretation of Trouton’s and Hildebrand’s rules for the entropy of vaporization of a liquid. J. Chem. Thermodyn. 2011, 43, 868–872. [Google Scholar] [CrossRef]
- Hensen, U.; Gräter, F.; Henchman, R.H. Macromolecular Entropy Can Be Accurately Computed from Force. J. Chem. Theory Comput. 2014, 10, 4777–4781. [Google Scholar] [CrossRef]
- Higham, J.; Chou, S.Y.; Gräter, F.; Henchman, R.H. Entropy of Flexible Liquids from Hierarchical Force-Torque Covariance and Coordination. Mol. Phys. 2018, 116, 1965–1976. [Google Scholar] [CrossRef]
- Irudayam, S.J.; Henchman, R.H. Entropic Cost of Protein-Ligand Binding and Its Dependence on the Entropy in Solution. J. Phys. Chem. B 2009, 113, 5871–5884. [Google Scholar] [CrossRef]
- Irudayam, S.J.; Henchman, R.H. Solvation theory to provide a molecular interpretation of the hydrophobic entropy loss of noble gas hydration. J. Phys. Condens. Matter 2010, 22, 284108. [Google Scholar] [CrossRef] [PubMed]
- Irudayam, S.J.; Plumb, R.D.; Henchman, R.H. Entropic trends in aqueous solutions of common functional groups. Faraday Discuss. 2010, 145, 467–485. [Google Scholar] [CrossRef]
- Irudayam, S.J.; Henchman, R.H. Prediction and interpretation of the hydration entropies of monovalent cations and anions. Mol. Phys. 2011, 109, 37–48. [Google Scholar] [CrossRef] [Green Version]
- Gerogiokas, G.; Calabro, G.; Henchman, R.H.; Southey, M.W.Y.; Law, R.J.; Michel, J. Prediction of Small Molecule Hydration Thermodynamics with Grid Cell Theory. J. Chem. Theory Comput. 2014, 10, 35–48. [Google Scholar] [CrossRef]
- Michel, J.; Henchman, R.H.; Gerogiokas, G.; Southey, M.W.Y.; Mazanetz, M.P.; Law, R.J. Evaluation of Host-Guest Binding Thermodynamics of Model Cavities with Grid Cell Theory. J. Chem. Theory Comput. 2014, 10, 4055–4068. [Google Scholar] [CrossRef]
- Gerogiokas, G.; Southey, M.W.Y.; Mazanetz, M.P.; Heifetz, A.; Bodkin, M.; Law, R.J.; Henchman, R.H.; Michel, J. Assessment of Hydration Thermodynamics at Protein Interfaces with Grid Cell Theory. J. Phys. Chem. B 2016, 120, 10442–10452. [Google Scholar] [CrossRef]
- Pascal, T.A.; Lin, S.T.; Goddard, W.A. Thermodynamics of liquids: Standard molar entropies and heat capacities of common solvents from 2PT molecular dynamics. Phys. Chem. Chem. Phys. 2011, 13, 169–181. [Google Scholar] [CrossRef]
- Lin, S.T.; Maiti, P.K.; Goddard, W.A. Two-Phase Thermodynamic Model for Efficient and Accurate Absolute Entropy of Water from Molecular Dynamics Simulations. J. Phys. Chem. B 2010, 114, 8191–8198. [Google Scholar] [CrossRef]
- Huang, S.N.; Pascal, T.A.; Goddard, W.A.; Maiti, P.K.; Lin, S.T. Absolute Entropy and Energy of Carbon Dioxide Using the Two-Phase Thermodynamic Model. J. Chem. Theory Comput. 2011, 7, 1893–1901. [Google Scholar] [CrossRef]
- Lai, P.K.; Lin, S.T. Rapid determination of entropy for flexible molecules in condensed phase from the two-phase thermodynamic model. RSC Adv. 2014, 4, 9522–9533. [Google Scholar] [CrossRef]
- Dodda, L.S.; Cabeza de Vaca, I.; Tirado-Rives, J.; Jorgensen, W.L. LigParGen web server: An automatic OPLS-AA parameter generator for organic ligands. Nucleic Acids Res. 2017, 45, W331–W336. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.M.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- Higham, J.; Henchman, R.H. Locally adaptive method to define coordination shell. J. Chem. Phys. 2016, 145, 084108. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Higham, J.; Henchman, R.H. Overcoming the limitations of cutoffs for defining atomic coordination in multicomponent systems. J. Comput. Chem. 2018, 39, 699–703. [Google Scholar] [CrossRef] [PubMed]
- Von Neumann, J. Mathematical Foundations of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1955. [Google Scholar]
- Case, D.A.; Berryman, J.T.; Betz, R.M.; Cerutti, D.S.; Cheatham, T.E., III; Darden, T.A.; Duke, R.E.; Giese, T.J.; Gohlke, H.; Goetz, A.W.; et al. AMBER 2015; University of California: San Francisco, CA, USA, 2015. [Google Scholar]
- Potoff, J.J.; Siepmann, J.I. Vapor-liquid equilibria of mixtures containing alkanes, carbon dioxide, and nitrogen. AICHE J. 2001, 47, 1676–1682. [Google Scholar] [CrossRef]
- Wang, J.M.; Wang, W.; Kollman, P.A.; Case, D.A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graph. Model. 2006, 25, 247–260. [Google Scholar] [CrossRef] [PubMed]
- Martinez, L.; Andrade, R.; Birgin, E.G.; Martinez, J.M. PACKMOL: A Package for Building Initial Configurations for Molecular Dynamics Simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schultz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Tirado-Rives, J. Potential energy functions for atomic-level simulations of water and organic and biomolecular systems. Proc. Natl. Acad. Sci. USA 2005, 102, 6665–6670. [Google Scholar] [CrossRef] [Green Version]
- National Institute of Standards and Technology. Standard Reference Database Number 69. In NIST Chemistry Webbook; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2018. [Google Scholar]
- Overstreet, R.; Giaque, W.F. Ammonia. The Heat Capacity and Vapor Pressure of Solid and Liquid. Heat of Vaporization. The Entropy Values from Thermal and Spectroscopic Data. J. Am. Chem. Soc. 1937, 59, 254–259. [Google Scholar] [CrossRef]
- Lide, D.R. (Ed.) CRC Handbook of Chemistry and Physics, 99th ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Younglove, B.; Ely, J. Thermo-physical Properties of Fluids. II. Methane, Ethane, Propane, Isotutane, and Normal Butane. J. Phys. Chem. Ref. Data 1987, 16, 577–798. [Google Scholar] [CrossRef]
- Giguère, P.A.; Liu, I.D.; Dugdale, J.S.; Morrison, J.A. Hydrogen peroxide—The low temperature heat capacity of the solid and the 3rd law entropy. Can. J. Chem. 1954, 32, 117–128. [Google Scholar] [CrossRef]
- Giaque, W.F.; Blue, R.W. Hydrogen Sulfide. The Heat Capacity and Vapor Pressure of Solid and Liquid. The Heat of Vaporization. A Comparison of Thermodynamic and Spectroscopic Values of the Entropy. J. Am. Chem. Soc. 1936, 58, 831–837. [Google Scholar] [CrossRef]
- Perry, R.H.; Green, D.W.; Maloney, J.O. Perry’s Chemical Engineers’ Handbook, 8th ed.; McGraw-Hill: New York, NY, USA, 2007. [Google Scholar]
- Stull, D.R.; Westrum, E.F., Jr.; Sinke, G.C. The Chemical Thermodynamics of Organic Compounds; Wiley: New York, NY, USA, 1969. [Google Scholar]
- Caleman, C.; van Maanen, P.J.; Hong, M.Y.; Hub, J.S.; Costa, L.T.; van der Spoel, D. Force Field Benchmark of Organic Liquids: Density, Enthalpy of Vaporization, Heat Capacities, Surface Tension, Isothermal Compressibility, Volumetric Expansion Coefficient, and Dielectric Constant. J. Chem. Theory Comput. 2012, 8, 61–74. [Google Scholar] [CrossRef] [PubMed]
- Blackburne, I.D.; Katritzky, A.R.; Takeuchi, Y. Conformation of piperidine and of derivatives with additional ring heteroatoms. Acc. Chem. Res. 1975, 8, 300–306. [Google Scholar] [CrossRef]




| Liquid | T/K | Liquid | T/K | Liquid | T/K | Liquid | T/K |
|---|---|---|---|---|---|---|---|
| ammonia | 240 | ethane | 185 | hydrogen sulfide | 213 | methylamine | 267 |
| butane | 272 | ethene | 170 | methane | 112 | propane | 231 |
| carbon dioxide | 220 | ethylamine | 291 | methanethiol | 279 | TFE | 197 |
| diazene | 275 |
| Data Set (Number of Liquids) | /J K mol | /J K mol | Slope | Y-Intercept/J K mol | Zero-Intercept Slope | |
|---|---|---|---|---|---|---|
| MCC OPLS (46) | 9.8 | 0.6 | 0.94 | 11.7 | 0.95 | 1.00 |
| MCC GAFF (50) | 8.7 | −0.3 | 0.93 | 13.0 | 0.96 | 0.99 |
| 2PT OPLS (12) | 15.5 | −15.6 | 1.05 | −25.3 | 0.84 | 0.92 |
| 2PT GAFF (14) | 28.0 | −24.4 | 0.97 | −19.5 | 0.55 | 0.87 |
| MCC OPLS (12) | 4.9 | 2.3 | 0.87 | 26.7 | 0.89 | 1.01 |
| MCC GAFF (14) | 7.6 | 4.0 | 0.93 | 16.5 | 0.93 | 1.02 |
| Liquid | Experiment | MCC | 2PT [48] | ||
|---|---|---|---|---|---|
| OPLS | GAFF | OPLS | GAFF | ||
| acetic acid | 158, 194 | 177 | 180 | 147 | 128 |
| acetone | 200 | 202 | 206 | 198 | 187 |
| acetonitrile | 150 | 143 | 145 | ||
| ammonia | 87 | 71 | 92 | ||
| aniline | 191, 192 | 205 | 205 | ||
| benzene | 173, 175 | 183 | 182 | 172 | 161 |
| benzyl alcohol | 217 | 216 | 208 | ||
| benzaldehyde | 221 | 204 | 204 | ||
| butane | 227, 230, 231 | 214 | 212 | ||
| butanol | 226, 228 | 244 | 235 | ||
| 2-butoxyethanol | 293 | 301 | |||
| carbon dioxide | 118 | 111 | 106 | 112 | |
| chloroform | 202 e | 203 | 210 | 193 | 226 |
| cyclohexane | 204, 206 | 220 | 212 | ||
| diazene | 121 | 125 | 116 | ||
| dichloromethane | 175 | 190 | 191 | ||
| diethanolamine | 248 | 256 | |||
| diethyl ether | 253, 254 | 237 | 236 | ||
| DMFA | 214 | 222 | |||
| DMSO | 189 | 183 | 202 | 164 | 159 |
| 1,4-dioxane | 197 | 206 | 199 | 179 | 159 |
| ethane | 127 | 125 | 127 | ||
| ethanol | 160, 161, 177 | 177 | 175 | 141 | 127 |
| ethene | 118 | 114 | 120 | ||
| ethyl acetate | 259 | 254 | 252 | ||
| ethylamine | 189 | 181 | 185 | ||
| ethylene glycol | 167, 180 | 172 | 175 | 141 | 121 |
| formamide | 151 | 153 | |||
| formic acid | 128, 132, 143 | 156 | 145 | ||
| furan | 177 | 181 | 186 | 167 | 157 |
| hexane | 290, 295, 296 | 273 | 272 | 251 | |
| hexanol | 287 | 288 | 281 | ||
| hydrazine | 122 | 120 | 116 | ||
| hydrogen peroxide | 110 | 126 | 125 | ||
| hydrogen sulfide | 106 | 101 | |||
| methane | 79 | 73 | 78 | ||
| methanethiol | 163 | 177 | 172 | ||
| methanol | 127, 130, 136 | 139 | 139 | 117 , 122 | 109 |
| methylamine | 150 | 128 | 133 | ||
| NMA | 205 | 206 | 181 | 168 | |
| octanol | 335 | 331 | |||
| pentane | 259, 263 | 251 | 250 | ||
| pentanol | 255, 259 | 264 | 257 | ||
| piperidine | 210 | 234 | 222 | ||
| propane | 171 | 176 | 176 | ||
| propanol | 193, 214 | 213 | 206 | ||
| pyridine | 178, 179, 210 | 191 | 189 | ||
| styrene | 238, 241 | 223 | 223 | ||
| TBA | 190, 198 | 218 | 217 | ||
| tetrahydrofuran | 204 | 188 | 192 | 196 | 159 |
| TFE | 184 | 207 | 195 | 185 | |
| toluene | 219, 221 | 224 | 223 | 204 | 190 |
| triethylamine | 309 | 292 | 295 | ||
| m-xylene | 252, 254 | 248 | 248 | ||
| o-xylene | 246, 248 | 245 | 245 | ||
| p-xylene | 244, 247, 253 | 243 | 243 | ||
| Component | Slope/J K g | Y-Intercept/J K mol | Component | Slope/J K g | Y-Intercept/J K mol | ||
|---|---|---|---|---|---|---|---|
| 0.21 | 50 | 0.54 | 0.42 | 14 | 0.63 | ||
| 0.35 | 28 | 0.70 | 0.43 | 6 | 0.34 | ||
| 0.09 | 16 | 0.13 | 0.39 | 16 | 0.87 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, H.S.; Higham, J.; Henchman, R.H. Entropy of Simulated Liquids Using Multiscale Cell Correlation. Entropy 2019, 21, 750. https://doi.org/10.3390/e21080750
Ali HS, Higham J, Henchman RH. Entropy of Simulated Liquids Using Multiscale Cell Correlation. Entropy. 2019; 21(8):750. https://doi.org/10.3390/e21080750
Chicago/Turabian StyleAli, Hafiz Saqib, Jonathan Higham, and Richard H. Henchman. 2019. "Entropy of Simulated Liquids Using Multiscale Cell Correlation" Entropy 21, no. 8: 750. https://doi.org/10.3390/e21080750
APA StyleAli, H. S., Higham, J., & Henchman, R. H. (2019). Entropy of Simulated Liquids Using Multiscale Cell Correlation. Entropy, 21(8), 750. https://doi.org/10.3390/e21080750