Surfing on Fitness Landscapes: A Boost on Optimization by Fourier Surrogate Modeling
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fuzzy Self-Tuning PSO (FST-PSO)
| Algorithm 1: Pseudocode of the FST-PSO algorithm. |
 |
2.2. Fitness Landscape Surrogate Modeling with Fourier Filtering (surF)
- a set of points, with , is defined by sampling f uniformly in ;
- a surrogate of f is defined in the following way, for each :
- (a)
- if is inside the convex hull of the points in A, then a triangulation of the points in A is constructed and the value of is obtained by linear interpolation. For example, in two dimensions, will be contained in a triangle defined by three points , and will be a linear combination of , , and ;
- (b)
- if is outside the convex hull of the points in A, then , where is the point in A that is nearest to .
| Algorithm 2: Pseudocode of the surF algorithm. |
 |
2.3. The Search on the Smoothed Landscape: Coupling surF with FST-PSO (F3ST-PSO)
- the surrogate model represents a smoothed version of the original fitness landscape, whose “smoothness” can be tuned by means of the hyperparameter;
- the evaluation of a candidate solution, using the surrogate model, requires a small computational effort. Notably, the latter can be far smaller than the evaluation of the original fitness function, especially in the case of real-world engineering or scientific problems (e.g., parameter estimation of biochemical systems [29], integrated circuits optimization [14], vehicle design [15]);
- even if an optimization performed on the surrogate model (e.g., using FST-PSO) does not require any evaluation of the original fitness function, it can provide useful information about the fitness landscape and the likely position of optimal solutions;
- the information about the optimal solutions found on the surrogate model can be used for a new optimization, leveraging the original fitness function.
- a part of the fitness evaluations budget is reserved for surF to randomly sample the search space and create the surrogate model;
- a preliminary optimization on the surrogate model is performed with FST-PSO, to identify an optimal solution ;
- a new FST-PSO instance is created, and is added to the initial random population;
- a new optimization is performed, exploiting the original fitness function and using the remaining budget of fitness evaluations;
- a new optimal solution is determined and returned as a result of the whole optimization.
2.4. Frequency of the Optimum Conjecture
3. Results and Discussion
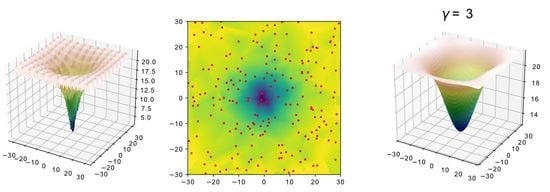
3.1. Generation of Surrogate Models by surF
3.2. Optimization of Benchmark Functions by F3ST-PSO
3.3. Optimization of the CEC 2005 TEST suite by F3ST-PSO
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| DFT | Discrete Fourier Transform |
| EC | Evolutionary Computation |
| FRBS | Fuzzy Rule Based System |
| FST-PSO | Fuzzy Self-Tuning Particle Swarm Optimization |
| F3ST-PSO | Fourier Filtering Fuzzy Self-Tuning Particle Swarm Optimization |
| PSO | Particle Swarm Optimization |
| surF | Surrogate modeling with Fourier filtering |
References
- Bhosekar, A.; Ierapetritou, M. Advances in surrogate based modeling, feasibility analysis, and optimization: A review. Comput. Chem. Eng. 2018, 108, 250–267. [Google Scholar] [CrossRef]
- Box, G.E.; Draper, N.R. Empirical Model-Building and Response Surfaces; John Wiley & Sons: Chichester, UK, 1987. [Google Scholar]
- Sacks, J.; Welch, W.J.; Mitchell, T.J.; Wynn, H.P. Design and analysis of computer experiments. Stat. Sci. 1989, 4, 409–423. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Ierapetritou, M. A novel feasibility analysis method for black-box processes using a radial basis function adaptive sampling approach. AIChE J. 2017, 63, 532–550. [Google Scholar] [CrossRef]
- Eason, J.; Cremaschi, S. Adaptive sequential sampling for surrogate model generation with artificial neural networks. Comput. Chem. Eng. 2014, 68, 220–232. [Google Scholar] [CrossRef]
- Lew, T.; Spencer, A.; Scarpa, F.; Worden, K.; Rutherford, A.; Hemez, F. Identification of response surface models using genetic programming. Mech. Syst. Signal Process. 2006, 20, 1819–1831. [Google Scholar] [CrossRef]
- Samad, A.; Kim, K.Y.; Goel, T.; Haftka, R.T.; Shyy, W. Multiple surrogate modeling for axial compressor blade shape optimization. J. Propuls. Power 2008, 24, 301–310. [Google Scholar] [CrossRef]
- Forrester, A.I.; Sóbester, A.; Keane, A.J. Multi-fidelity optimization via surrogate modelling. Proc. R. Soc. A Math. Phys. Eng. Sci. 2007, 463, 3251–3269. [Google Scholar] [CrossRef]
- Viana, F.A.; Haftka, R.T.; Watson, L.T. Efficient global optimization algorithm assisted by multiple surrogate techniques. J. Glob. Optim. 2013, 56, 669–689. [Google Scholar] [CrossRef]
- Zhou, Z.; Ong, Y.S.; Nair, P.B.; Keane, A.J.; Lum, K.Y. Combining global and local surrogate models to accelerate evolutionary optimization. IEEE Trans. Syst. Man Cybern. Part C 2006, 37, 66–76. [Google Scholar] [CrossRef] [Green Version]
- Forrester, A.I.; Keane, A.J. Recent advances in surrogate-based optimization. Prog. Aerosp. Sci. 2009, 45, 50–79. [Google Scholar] [CrossRef]
- Queipo, N.V.; Haftka, R.T.; Shyy, W.; Goel, T.; Vaidyanathan, R.; Tucker, P.K. Surrogate-based analysis and optimization. Prog. Aerosp. Sci. 2005, 41, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Zhang, Q.; Gielen, G.G. A Gaussian process surrogate model assisted evolutionary algorithm for medium scale expensive optimization problems. IEEE Trans. Evol. Comput. 2013, 18, 180–192. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Zeng, W.; Qiu, W.S.; Wang, T. Optimization of the suspension parameters of a rail vehicle based on a virtual prototype Kriging surrogate model. Proc. Inst. Mech. Eng. Part J. Rail Rapid Transit 2016, 230, 1890–1898. [Google Scholar] [CrossRef]
- Jin, Y. Surrogate-assisted evolutionary computation: Recent advances and future challenges. Swarm Evol. Comput. 2011, 1, 61–70. [Google Scholar] [CrossRef]
- Sun, C.; Jin, Y.; Cheng, R.; Ding, J.; Zeng, J. Surrogate-assisted cooperative swarm optimization of high-dimensional expensive problems. IEEE Trans. Evol. Comput. 2017, 21, 644–660. [Google Scholar] [CrossRef] [Green Version]
- Tang, Y.; Chen, J.; Wei, J. A surrogate-based particle swarm optimization algorithm for solving optimization problems with expensive black box functions. Eng. Optim. 2013, 45, 557–576. [Google Scholar] [CrossRef]
- Branke, J. Creating robust solutions by means of evolutionary algorithms. In International Conference on Parallel Problem Solving from Nature; Springer: Berlin/Heidelberger, Germany, 1998; pp. 119–128. [Google Scholar]
- Yu, X.; Jin, Y.; Tang, K.; Yao, X. Robust optimization over time—A new perspective on dynamic optimization problems. In Proceedings of the IEEE Congress on evolutionary computation, Barcelona, Spain, 18–23 July 2010; pp. 1–6. [Google Scholar]
- Bhattacharya, M. Reduced computation for evolutionary optimization in noisy environment. In Proceedings of the 10th Annual Conference Companion on Genetic and Evolutionary Computation, New York, NY, USA, 21–24 July 2008; pp. 2117–2122. [Google Scholar]
- Yang, D.; Flockton, S.J. Evolutionary algorithms with a coarse-to-fine function smoothing. In Proceedings of the 1995 IEEE International Conference on Evolutionary Computation, Perth, WA, Australia, 29 November–1 December 1995; pp. 657–662. [Google Scholar]
- Nobile, M.S.; Cazzaniga, P.; Besozzi, D.; Colombo, R.; Mauri, G.; Pasi, G. Fuzzy Self-Tuning PSO: A settings-free algorithm for global optimization. Swarm Evol. Comp. 2018, 39, 70–85. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Tangherloni, A.; Spolaor, S.; Cazzaniga, P.; Besozzi, D.; Rundo, L.; Mauri, G.; Nobile, M.S. Biochemical parameter estimation vs. benchmark functions: A comparative study of optimization performance and representation design. Appl. Soft Comput. 2019, 81, 105494. [Google Scholar] [CrossRef]
- SoltaniMoghadam, S.; Tatar, M.; Komeazi, A. An improved 1-D crustal velocity model for the Central Alborz (Iran) using Particle Swarm Optimization algorithm. Phys. Earth Planet. Inter. 2019, 292, 87–99. [Google Scholar] [CrossRef]
- Fuchs, C.; Spolaor, S.; Nobile, M.S.; Kaymak, U. A Swarm Intelligence approach to avoid local optima in fuzzy C-Means clustering. In Proceedings of the 2019 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), New Orleans, LA, USA, 23–26 June 2019; pp. 1–6. [Google Scholar]
- Cooley, J.W.; Tukey, J.W. An algorithm for the machine calculation of complex Fourier series. Math. Comput. 1965, 19, 297–301. [Google Scholar] [CrossRef]
- Nobile, M.S.; Tangherloni, A.; Besozzi, D.; Cazzaniga, P. GPU-powered and settings-free parameter estimation of biochemical systems. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 32–39. [Google Scholar]
- Oliphant, T.E. A Guide to NumPy; Trelgol Publishing: Spanish Fork, UT, USA, 2006. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0–Fundamental Algorithms for Scientific Computing in Python. arXiv 2019, arXiv:1907.10121. [Google Scholar] [CrossRef] [Green Version]
- Matsumoto, M.; Nishimura, T. Mersenne twister: A 623-dimensionally equidistributed uniform pseudo-random number generator. ACM Trans. Model. Comput. Simul. 1998, 8, 3–30. [Google Scholar] [CrossRef] [Green Version]
- Gibbs, J.W. Fourier’s series. Nature 1899, 59, 606. [Google Scholar] [CrossRef]
- Schwefel, H.P. Numerical Optimization of Computer Models; John Wiley & Sons: Chichester, UK, 1981. [Google Scholar]
- Suganthan, P.N.; Hansen, N.; Liang, J.J.; Deb, K.; Chen, Y.P.; Auger, A.; Tiwari, S. Problem definitions and evaluation criteria for the CEC 2005 special session on real-parameter optimization. KanGAL Rep. 2005, 2005005, 2005. [Google Scholar]
- Nobile, M.S.; Cazzaniga, P.; Ashlock, D.A. Dilation functions in global optimization. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 2300–2307. [Google Scholar]
- Nobile, M.S.; Besozzi, D.; Cazzaniga, P.; Mauri, G.; Pescini, D. A GPU-based multi-swarm PSO method for parameter estimation in stochastic biological systems exploiting discrete-time target series. In European Conference on Evolutionary Computation, Machine Learning and Data Mining in Bioinformatics; Springer: Berlin/Heidelberger, Germany, 2012; pp. 74–85. [Google Scholar]
- Sobol’, I.M. On the distribution of points in a cube and the approximate evaluation of integrals. Zhurnal Vychislitel’Noi Mat. Mat. Fiz. 1967, 7, 784–802. [Google Scholar] [CrossRef]
- Manzoni, L.; Mariot, L. Cellular Automata pseudo-random number generators and their resistance to asynchrony. In International Conference on Cellular Automata; Springer: Berlin/Heidelberger, Germany, 2018; pp. 428–437. [Google Scholar]
- Ye, K.Q. Orthogonal column Latin hypercubes and their application in computer experiments. J. Am. Stat. Assoc. 1998, 93, 1430–1439. [Google Scholar] [CrossRef]







| Function | Equation | Search Space | Value in Global Minimum |
|---|---|---|---|
| Ackley | |||
| Alpine | |||
| Griewank | |||
| Michalewicz | , in this work | ||
| Rastrigin | |||
| Rosenbrock | |||
| Schwefel | |||
| Shubert | Many global minima, whose values depend on D | ||
| Vincent | |||
| Xin-She Yang n.2 |
| Setting | Value |
|---|---|
| Fitness evaluations budget | 13,000 |
| 500 | |
| 40 | |
| values tested | 3, 5 and 15 |
| Swarm size F3ST-PSO | 25 |
| Iterations F3ST-PSO | 500 |
| Swarm size of FST-PSO | 25 |
| Iterations FST-PSO | 520 |
| Setting | Value |
|---|---|
| Fitness evaluations budget | 25,500 |
| 500 | |
| 40 | |
| values tested | 3, 5 and 15 |
| Swarm size F3ST-PSO | 25 |
| Iterations F3ST-PSO | 1000 |
| Swarm size of FST-PSO | 25 |
| Iterations FST-PSO | 1020 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manzoni, L.; Papetti, D.M.; Cazzaniga, P.; Spolaor, S.; Mauri, G.; Besozzi, D.; Nobile, M.S. Surfing on Fitness Landscapes: A Boost on Optimization by Fourier Surrogate Modeling. Entropy 2020, 22, 285. https://doi.org/10.3390/e22030285
Manzoni L, Papetti DM, Cazzaniga P, Spolaor S, Mauri G, Besozzi D, Nobile MS. Surfing on Fitness Landscapes: A Boost on Optimization by Fourier Surrogate Modeling. Entropy. 2020; 22(3):285. https://doi.org/10.3390/e22030285
Chicago/Turabian StyleManzoni, Luca, Daniele M. Papetti, Paolo Cazzaniga, Simone Spolaor, Giancarlo Mauri, Daniela Besozzi, and Marco S. Nobile. 2020. "Surfing on Fitness Landscapes: A Boost on Optimization by Fourier Surrogate Modeling" Entropy 22, no. 3: 285. https://doi.org/10.3390/e22030285
APA StyleManzoni, L., Papetti, D. M., Cazzaniga, P., Spolaor, S., Mauri, G., Besozzi, D., & Nobile, M. S. (2020). Surfing on Fitness Landscapes: A Boost on Optimization by Fourier Surrogate Modeling. Entropy, 22(3), 285. https://doi.org/10.3390/e22030285