Next Article in Journal
Discrimination of Chrysanthemum Varieties Using Hyperspectral Imaging Combined with a Deep Convolutional Neural Network
Next Article in Special Issue
Hydration Thermodynamics of Non-Polar Aromatic Hydrocarbons: Comparison of Implicit and Explicit Solvation Models
Previous Article in Journal
Phytochemical and Biological Profile of Moricandia arvensis (L.) DC.: An Inhibitor of Pancreatic Lipase
Previous Article in Special Issue
A Comparison of QM/MM Simulations with and without the Drude Oscillator Model Based on Hydration Free Energies of Simple Solutes
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 23
Issue 11
10.3390/molecules23112830
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Polarizable ab initio QM/MM Study of the Reaction Mechanism of N-tert-Butyloxycarbonylation of Aniline in [EMIm][BF4]

by
Erik Antonio Vázquez-Montelongo
1,
José Enrique Vázquez-Cervantes
1 and
G. Andrés Cisneros
1,2,*
1
Department of Chemistry, University of North Texas, Denton, TX 76201, USA
2
The Center for Advanced Scientific Computing and Modeling (CASCaM), University of North Texas, Denton, TX 76201, USA
*
Author to whom correspondence should be addressed.
Molecules 2018, 23(11), 2830; https://doi.org/10.3390/molecules23112830
Submission received: 9 October 2018 / Revised: 27 October 2018 / Accepted: 29 October 2018 / Published: 31 October 2018
(This article belongs to the Special Issue Combined Quantum Mechanical and Molecular Mechanical Methods and Simulations)
Browse Figures
Versions Notes

Abstract

:
N- t e r t -butoxycarbonylation of amines in solution (water, organic solvents, or ionic liquids) is a common reaction for the preparation of drug molecules. To understand the reaction mechanism and the role of the solvent, quantum mechanical/molecular mechanical simulations using a polarizable multipolar force field with long–range electrostatic corrections were used to optimize the minimum energy paths (MEPs) associated with various possible reaction mechanisms employing the nudged elastic band (NEB) and the quadratic string method (QSM). The calculated reaction energies and energy barriers were compared with the corresponding gas-phase and dichloromethane results. Complementary Electron Localization Function (ELF)/NCI analyses provide insights on the critical structures along the MEP. The calculated results suggest the most likely path involves a sequential mechanism with the rate–limiting step corresponding to the nucleophilic attack of the aniline, followed by proton transfer and the release of CO 2 without the direct involvement of imidazolium cations as catalysts.

Graphical Abstract

1. Introduction

Ionic liquids (ILs) are molten salts composed of (usually) organic cations and inorganic or organic anions. An interesting feature of many of these cation/anion mixtures is that they are liquid at room temperature (RTIL) [1,2]. The very large number of available combinations of anions and cations (and their structural features) results in a myriad variations of physicochemical properties, such as relatively low viscosity [3], virtually nonexistent vapor pressure, high thermal conductivity, to name a few [1,2,3,4]. ILs have been use in a wide range of applications, such as electrochemistry [5] (nonaqueous electrolyte) and for applications in synthetic chemistry. Recently, these liquids have been used as an alternative for organic solvents in enzymatic catalysis [6,7,8].
ILs provide an attractive alternative to organic solvents for several applications due to their immiscibility with many solvents (even with water), and because they are nonvolatile, nonflammable, and thermally stable liquids [3,9,10,11]. Additionally, their exceptional solvation and dissolution properties make them useful solvents for homogeneous catalysis [3,12,13]. One particular example involves the protection reaction of primary amines. Sarkar et al. have proposed that ILs based on 1-alkyl-3-methylimidazolium may act as catalysts for the efficient N-tert-butoxycarbonylation of amines with good chemoselectivity [14]. However, other studies have proposed that this reaction proceeds via a catalyst-free mechanism [15,16].
Computational simulations have become a useful tool to investigate IL properties given the very large number of possible combinations. Simulations based on classical molecular dynamics using nonpolarizable point charges have shown to provide insights into these systems [17,18,19,20,21,22,23,24]. It has been shown that the inclusion of polarization can improve the description of IL-based systems [25,26,27,28,29,30]. Some of us have extended AMOEBA to investigate a variety of IL systems [31,32,33,34,35,36,37]. AMOEBA is a multipolar/polarizable potential that relies on distributed atomic multipoles up to quadrupoles and inducible point dipoles [38,39,40]. We have shown that distributed multipoles obtained fitting electronic densities via the Gaussian electrostatic model (GEM) can provide accurate multipoles for several systems, including ILs [31,41,42,43].
Computational simulations have also been employed to investigate reaction mechanisms of chemical reactions in ILs using quantum-mechanics/molecular-mechanics (QM/MM) simulations [44,45,46,47,48,49,50]. Nonpolarizable force fields (NPFF) such as OPLS [51], CHARMM [52,53], AMBER [54,55], or GROMOS [56], have been typically used to model the classical environment in the QM/MM system, and to study solute–solvent interactions, conformational changes, and reaction mechanisms in ILs and other types of systems, such as biological and condensed-phase systems [57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74].
Polarization has also been shown to be important in QM/MM simulations [29,75,76,77,78,79,80,81]. However, to our knowledge, there have been no QM/MM simulations of reactions in IL systems that include an explicitly polarizable MM environment. In this contribution, we present the use of AMOEBA-based polarizable ab initio QM/MM simulations to investigate the reaction mechanism of the N-tert-butoxycarbonylation of aniline (base reaction for the preparation of drug molecules [82]) in a water/1-ethyl, 3-methyl imidazolium/tetrafluoroborate ([EMIm][BF 4 ]) mixture. Complementary combined electron localization function (ELF)/noncovalent interaction (NCI) [83,84,85,86,87,88,89,90] analyses were used to gain insights on the solvent–solvent, solvent–solute, and solute–solute intra- and intermolecular interactions.
The remainder of the paper is organized as follows: in the next section, we present the computational methodology for the calculation of the required AMOEBA parameters, details of the QM/MM and QM simulations for the reference gas-phase and implicit-solvent reaction, as well as the corresponding cross ELF/NCI analyses. Subsequently, we present the results for the considered reaction mechanisms, followed by concluding remarks.

2. Methodology

This section presents the details of the computational methods and procedures employed for the parametrization of aniline and di-tert-butyl dicarbonate [(Boc) 2 O] for AMOEBA, followed by a description of the QM methods and the procedure for the QM/MM simulations using LICHEM for the determination of the reactants and products, as well as the minimum energy paths (MEPs).

2.1. Parametrization

AMOEBA parameters for [EMIm][BF 4 ] have been previously reported [34,35]. The parameters for aniline and di-tert-butyl dicarbonate molecules for AMOEBA [38,39,40] were obtained following the methodology previously described [32,33,34,40]. The bonded parameters were taken from available parameters for similar molecules without any adjustment [40]. The nonbonded (electrostatic, polarization, and van der Waals) parameters were fitted based on QM energy-decomposition analysis (EDA) [32,33,34]. Briefly, the EDA-based nonbonded parametrization procedure was performed as follows: (1) calculation of basis set superposition error (BSSE)-corrected total intermolecular energies between aniline/[(Boc) 2 O] and water dimers oriented randomly at the ω B97XD/aug-cc-pVTZ level of theory using the Gaussian09 software package [91]; (2) computation of the electrostatic and polarization contributions for the same dimers using Symmetry-Adapted Perturbation Theory (SAPT) with Psi4 [92], at the SAPT0/6-311+G(d,p) level of theory; (3) calculation and optimization of GEM distributed multipoles (GEM-DM) using GEM-fit [31] by minimization of the Coulomb intermolecular interaction error with respect to the SAPT Coulomb reference.

2.2. Molecular-Dynamics Simulations

Molecular-dynamics (MD) simulations of a mixture of 7410 water molecules and 189 [EMIM][BF4] ion pairs, corresponding to a 2.5% mol solution of IL, were performed using AMOEBA [38,39,40], employing the TINKER–OpenMM software package [93]. The system was equilibrated for 1 ns using the RESPA integrator, 2 fs time step, and the Bussi thermostat. Subsequently, one molecule of aniline and one molecule of [(Boc) 2 O] were placed in the center of the equilibrated water/IL mixture. The closest cation and anion pair to the solute molecules was manually repositioned to within 3 Å of the solvent molecules. The resulting solute/solvent system was subjected to a 1 ns MD with a distance constraint of 15 (kcal/mol)/Å 2 between the solute and nearest ion pair molecules. Finally, the distance constraint between the aniline/[(Boc) 2 O] and the ionic pair was removed and the system was subjected to unrestrained MD for 1 ns.

2.3. Gas-Phase and Implicit Solvent Calculations

The critical structures (reactants, products, intermediates, and transition states) for each of the tested schemes were optimized in the gas phase and in implicit solvent (CH 2 Cl 2 ) at the ω B97XD [94] level of theory with the 6-31G(d) [95] basis set using Gaussian09 [91]. For transition state optimization, the Synchronous Transition Quasi-Newton (STQN) method [96] was used (implemented as QST3 in Gaussian09). Frequency calculations for reactant, intermediate, product, and transition state were performed. All thermochemistry calculations were carried out at STP conditions.

2.4. QM/MM Geometry and Reaction-Path Optimizations

All QM/MM calculations were performed using the LICHEM software package [81]. The QM region (aniline + di-tert-butyl dicarbonate + one IL pair + water) was calculated at the ω B97XD level of theory using the 6-31G(d) basis set. Two QM/MM simulation systems were created based on the above MD simulations, one with the ion pair close to the solute (C1), and one after the constraints had been released (C2). The QM regions for both systems were selected based on the number of molecules around an 8 Å sphere with respect to a central C on the (Boc) 2 O molecule (see below). In all cases, the QM/MM systems did not involve covalent bonds across the QM/MM regions. The MM region (26688 atoms) was modeled using the AMOEBA force field. Long-range electrostatic (LRE) effects were taken into account using LRE correction (LREC) approximation [97,98], with an LREC exponent of 2 and a cutoff radius of 20 Å.
Path optimizations for the QM/MM systems were performed by means of two chain-of-replica methods, the nudged elastic band (NEB) or quadratic string method (QSM) [99,100]. A linear interpolation between the reactant and product structures was performed using 17–19 beads to generate the initial guess for the replicas along the chain using the path utility in LICHEM. For the NEB optimizations, 20 path optimization steps and 20 QM optimization steps were used for the geometry and reaction-path calculations using a spring constant of 1 eV/Å 2 . The QM tolerance was set to a RMS deviation of 0.001 Å, RMS force of 0.005 Hartree/Bohr, and maximum RMS force to 0.02 Hartree/Bohr. MM tolerance was set to a RMS deviation of 0.2 Å and a RMS force of 0.2 kcal/Å.
In some cases, it has been observed that the use of a second-order path optimizer such as QSM can provide a way to refine or overcome convergence issues for first-order path optimization methods [72,101]. We have recently implemented QSM in LICHEM [100,102]. In QSM, each replica on the MEP is perpendicularly minimized to the reaction coordinate direction through a quadratic surface approximated by a damped Broyden–Fletcher–Goldfarb–Shanno (BFGS)-updated Hessian, followed by an N-order Runge–Kutta adaptive step-size integration method.The same settings/tolerances as above, for the NEB paths, were employed for the QSM-optimized paths. Both NEB and QSM lack explicit TS optimizers, and thus the highest energy points obtained from the optimized MEPs are only approximations of the corresponding TS [99,100].

2.5. Combined ELF/NCI Analyses

All wave functions for the ELF and NCI calculations were obtained using the LICHEM software package [81], with the same level of theory used for the QM/MM calculations. ELF calculations were computed with the ToPMoD software package [103,104], using a cubic grid of 200 a.u. with a step size of 0.1 a.u., with an isovalue of 0.83. For the NCI calculations, the NCIPLOT software package [87] was used, with an isovalue of 0.5 au with the color scale with a range of −0.05 au < sign( λ 2) ρ < 0.05 au.

3. Results and Discussion

3.1. Parametrization Results

The GEM-distributed multipoles (GEM-DM) for the solute molecules were obtained by fitting electronic densities at the DFT level for each molecule as described above. Molecular densities were optimized by minimizing the error of the intermolecular Coulomb interaction between the fitted density of the target molecule and a water molecule with respect to the Coulomb component from SAPT0 for a set of solvent/water dimers in random orientations to ensure transferabitliy [34,35,58].
The comparison between the electrostatic contribution from SAPT0 calculations and the GEM-DM is shown in Figure 1. Previous studies have shown that intermolecular electrostatic interactions calculated with GEM-DM are well described at medium and long range [32,33,34], and deviations arise at short intermolecular distances due to penetration errors [105].
The Van der Waals parameters were obtained by fitting the corresponding contributions by a subtractive approach using the BSSE-corrected total intermolecular interaction energies and SAPT0-calculated components, and comparing with the respective AMOEBA/GEM-DM counterparts [34,35,58]. The total intermolecular interactions (BSSE-corrected and SAPT0) show good agreement with the final set of parameters (see Figures S1 and S2).

3.2. Optimizations of Critical Points

Four different reaction path possibilities were tested for the N- t e r t -butyloxycarbonylation of aniline based on previously proposed mechanisms (Scheme 1) [14,15]. The first two possibilities (Scheme 1a,b) involve the activation of (Boc) 2 O through the formation of a bifurcated hydrogen bond between a water or cation ([EMIM] + ) molecule, respectively. This step is followed by a nucleophilic attack by the aniline N, formation t e r t -butyl carbamate and t e r t -butyl carboxylic acid, and, finally, the release of CO 2 from this acid and formation of t e r t -butanol.
The remaining two proposed mechanisms, shown in Scheme 1c,d, involve a possible sequential path without the involvement of an explicit activating molecule for (Boc) 2 O. Depending on which O atom from (Boc) 2 O accepts the leaving proton from the aniline, the formation of CO 2 can proceed with or without the formation of t e r t -butyl carboxylic acid (Scheme 1c,d, respectively).
Based on the mechanistic possibilities described above, two different QM/MM systems were studied based on two configurations of an IL ion pair. The first configuration (C1) was obtained by optimizing a series of snapshots from the MD simulation where the ion pair distance was restrained (Figure 2a) by selecting 149 atoms to be located in the QM region (see Section 2.4). The second configuration, termed C2, was obtained based on the QM/MM optimization of a series of snapshots from the unrestrained MD simulation (Figure 2b) by selecting 155 atoms to be located in the QM region (see Section 2.4). In particular, in C1, the IL cation forms an H-bonding interaction in between both oxygens from the [(Boc) 2 O] carbonyl groups, whereas in C2, there are no specific interactions with [(Boc) 2 O]. These two configurations were subsequently employed to test all four mechanistic possibilities described above by optimizing the reactant and product structures at the QM/MM level for all four possible mechanisms in Scheme 1.
The calculated reaction energies for the reactions in Scheme 1a,b are highly endothermic (Table 1). Therefore, these two mechanistic possibilities were not further considered. Conversely, the reaction energies for Scheme 1c,d in the water/IL solution were found to be exothermic.
Geometry optimizations in gas phase (GP) and in dichloromethane (DCM) using the SMD implicit solvent model were performed for structures in Scheme 1c,d for comparison purposes. In all cases, the calculated reaction energies were found to be exothermic; for Scheme 1c, the DCM(GP) reaction energies were −16.11(−17.26), compared with −9.53(−0.19) for Scheme 1d. These results suggest that the water/IL mixture provides significant stabilization of the product structures compared to GP or pure organic solvent (as represented with an implicit solvent model).

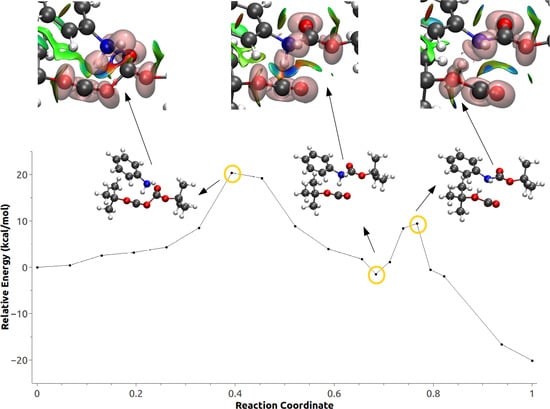
3.3. Minimum Energy Path Optimizations

The two possible mechanisms (Scheme 1c,d) were further investigated in the water/IL QM/MM systems by determining the minimum energy paths connecting the reactant and product structures. Four MEPs were tested to investigate the reaction path for each possible scheme with either configuration 1 (C1, nearby IL ion pair) or configuration 2 (C2). As described above, Scheme 1c corresponds to the nucleophilic attack without the simultaneous formation of CO 2 , while Scheme 1d includes the concomittant formation of CO 2 after the formation of the carbamate.
The calculated MEP for Scheme 1c using Configuration C1 (Figure 3 and Video S1) suggest that this path proceeds through an SN 2 -like mechanism, starting with the nucleophilic attack by the aniline to the carbonyl of one of the Boc groups and the concommitant bond breaking of an O–C bond in Boc–O–Boc (transition state). This is followed by a proton transfer from the amine to the Boc group, and the corresponding formation of the t e r t -butyl carbamate and t e r t -butyl carboxylic acid. The highest point on the path has an energy barrier of 24.28 kcal/mol with respect to the reactant structure. Two products were observed along with this MEP, which correspond to two different orientations of the hydroxyl H formed after the proton transfer from the aniline. The final product (Product 2 in Figure 3) was around 8 kcal/mol lower in energy than the initially optimized product.
A similar reaction path to the one calculated for Configuration C1 was found for Scheme 1c using Configuration C2 (Figure 4 and Video S2). The major differences between the two configurations involve a reduction of around 3 kcal/mol in barrier height for C2 compared with C1, and no observed rotation of the H bond to form a second product. Interestingly, the change in the anisotropic field by having the IL ion pairs further away resulted in the stabilization of a metastable intermediate (MI) corresponding to the product of the nucleophylic attack, but prior to the proton transfer, coupled with a second low-barrier TS associated with the proton transfer, and leading to the formation of the product. The resulting product structures for both configurations (product 1 for Figure 3) showed very similar geometries and relative energies (C1: Δ E = −20.46 kcal/mol, C2: Δ E = −20.88 kcal/mol).
In the case of Scheme 1d, path optimization for the system corresponding to Configuration C1 failed to converge with both NEB and QSM. In both cases, the path exhibited several discontinuities, which could be due to the close proximity of the highly charged ion pair. The QSM-optimized MEP for Scheme 1d with Configuration C2 is presented in Figure 5 (and Video S3). The rate-limiting step had a barrier of 20.42 kcal/mol, which corresponds to the nucleophilic attack of the aniline to the carbonyl of one of the Boc groups, followed by a metastable intermediate and a second energy barrier (1.18 kcal/mol and 9.47 kcal/mol, respectively) corresponding to the proton transfer from the amine to the Boc group, and the subsequent formation of the t e r t -butanol, CO 2 , and t e r t -butyl carbamate.
For the GP and DCM calculations, TS optimizations were performed using the QST3 method [96]. The calculated energy barriers for Scheme 1c corresponded to 24 kcal/mol and 17.64 kcal/mol, respectively (Figure 6). For Scheme 1d, optimization failed to yield TS structures that connect the reactant and product valleys for both the GP and DCM systems.
Previous experimental reports have suggested that this reaction shows very low yields in DCM, and high yields with good stereoselectivity in ILs [14]. The present DCM results suggest the availability of a path to form the protected aniline, but we were unable to find a viable route to the final products, including formation of CO 2 , via either Scheme 1c or d. Conversely, for the water/IL mixture, the path optimization results suggested Scheme 1d was the most likely mechanism.

3.4. Population and Topological Analyses for Critical Structures

Complementary topological and population analysis has been carried out to gain further insights on the electronic structure and its evolution for critical points along the path. The ESP charge population analysis for the atoms involved in the reaction (Figure 7) for the reaction mechanisms using configuration C2 are presented in Figure 8 for Scheme 1c,d (see Figure S4 for configuration C1).
In the case of Scheme 1c, an increase in charge around the TS was observed for the four atoms involved in the bond-formation/-breaking processes. In particular, atoms N(43) and C(1) show an increase in charge, which is anticorrelated with a decrease in charge for O(13). These results are consistent with the changes in charge observed for the GP and DCM critical points (see Table 2). For Scheme 1d, a significant change in the nitrogen charge was also observed, although the charge appeared to be distributed among the remaining atoms in the system, and not only the atoms directly involved in the bond-breaking/-forming processes.
For the reaction in GP and DCM for Scheme 1c (Table 2), the results were consistent with the ones in the water/IL mixture. Similarly, there was a decrease of the charge for O(13) and an increase for N(43). This behavior could be due to the presence of two ionic species in the transition state (Boc-O − and Boc-Ph-NH 2 + ), a result of the aniline nucleophilic attack.
Combined ELF/NCI analyses have been used to provide better insights into chemical bonding and weak noncovalent interactions, as well to understand reaction mechanisms in organic and biological systems [58,64,88,89,90]. The combined ELF/NCI analyses for the TS structures for the rate-limiting step in Scheme 1c for all tested systems (GP, DCM, and Configurations C1 and C2) are shown in Figure 9 (see Figures S5–S8 for all ELF/NCI analyses for all critical structures).
The TS structures for Scheme 1c in all four systems show a disynaptic basin between C1 and N43 in the ELF region between these atoms (pink transparent surface in Figure 9 and Table 3), which corresponds to the formation of the covalent bond resulting from the nucleophilic attack of the aniline on the carbonyl C of Boc. That is, in all cases, the TS structure corresponding to this nucleophilic attack already involved a bond between the N and C atoms, which would suggest that these structures corresponded to a late TS.
In addition, a strong hydrogen bond (H–bond) interaction was observed between H(45) and O(11) for the TSs in the gas-phase and dichloromethane systems (depicted as a large dark-blue surface in Figure 9a,b). Conversely, the TS structures corresponding to the water/IL solution did not exhibit this strong H–bond, which was due to the change in the nucleophilic attack orientation of the aniline due to the stabilization of the surrounding solvent.
The results of ELF population and distributed multipole analyses for the selected basins are presented in Table 3 (see Tables S1–S5 for full multipolar analysis). Overall, the results were in agreement with the corresponding ESP charge population analysis. In particular, a disynaptic basin was observed, V(C1,N43), corresponding to the nucleophilic attack surface discussed above. Interestingly, the population and first polar moment for this basin in TS1 for the reaction in the water/IL mixture was considerably larger than in GP and DCM. In addition, for the water/IL mixture, a monosynaptic basin for the transferring proton was observed, V(H45). This basin was indicative of a strong H–bond interaction. These basins were previously shown to indicate strong interactions, such as low-barrier hydrogen bonds.
By contrast, the TS structure for Scheme 1d did not exhibit a disynaptic basin between the attacking N and C atoms. Instead, a ring was observed on the NCI surface in Figure 10b, indicating a strong attractive interaction, although no basin was observed in the ELF analysis. These results suggest that the solvent environment for Scheme 1d stabilized an early TS. Additionally, Figure 10c shows a bifurcated H–bond interaction between H45, O11, and O13, which was resolved in TS2 with the transfer of H49 to O11 (Table 4). Interestingly, no NCI surfaces were observed between the H(45) and N(43), in the TS2, or the product structure, indicating an increase in distance between the resulting product molecules.

3.5. Effect of Polarization on the Reaction Path

The MEPs for Scheme 1c,d for Configuration C2 were reoptimized without explicit polarization to investigate the role of polarization of the environment on the reaction path (Figure 11). For Scheme 1c, the resulting energy profile was similar to the one with the use of explicit polarization (Figure 4), with an energy barrier of 21.43 kcal/mol and a reaction energy of −36.87 kcal/mol. However, this MEP lacked the second TS that corresponds to the proton transfer. For Scheme 1d, the energy profile showed some irregularities due to the rearrangement of environmental solvent molecules (see Video S4 for Scheme 1c, Configuration C2; and Video S5 for Scheme 1d, Configuration C2 for supporting information), an energy barrier of 39.67 kcal/mol (almost twice the value for the MEP shown in Figure 5), and a reaction energy of −21.01 kcal/mol. The similarities observed between the energy profiles with and without polarization may be due to the fact that path optimization was performed using the optimized path with polarization as an initial guess for the unpolarized MEP optimization, and the fact that the optimized path corresponded to the potential energy surface, and not the free energy surface. Previously, we showed the importance of the inclusion of explicit polarization of the MM environment due to the QM region, and the polarization of the QM region due to the static field [81], and the importance of polarization in classical simulations on a neutral but highly polarizable ligand [106].
The ESP charges for selected atoms in the TS1 for both Scheme 1c,d (see Figures S9 and S10) indicate a charge redistribution in the neighboring atoms of C1 and N43, and there was a large difference in the charge of the aniline nitrogen (N43) when polarization from the MM environment is considered or not. Inclusion of thermal and entropic effects (e.g., by FEP) would be useful to provide further insights to understand these effects.

4. Conclusions

The reaction mechanism for the N- t e r t -butyloxycarbonylation of aniline in a water/IL mixture was investigated by means of polarizable QM/MM calculations. Based on our results, the reaction was observed to involve either a concerted or sequential reaction mechanism, depending on the configuration of the ionic pair. The rate-limiting step was found to correspond to the nucleophilic attack of the aniline. In addition, the products that were formed depend on which accepting O atom received the proton transferred from the amine N, resulting in two possible reaction mechanisms. The results from the combined ELF/NCI analyses suggest that, for the mechanism where no CO 2 was formed (Scheme 1c), the rate-limiting step was suggestive of a late TS. Conversely, for the path where CO 2 was formed (Scheme 1d), an early TS structure appeared to be stabilized by the surrounding environment. Additionally, the ELF results suggest that the proton transferred from the aniline in the second stage of the reaction involved a strong H–bond interaction similar to an LBHB for Scheme 1c compared with Scheme 1d, where the proton transfer occurred after the rate-limiting barrier was overcome. The inclusion of explicit polarization of the MM environment was observed to play an important role in the energetics of the MEP and the charge density distribution of the QM subsystem.

Supplementary Materials

The following are available online at https://www.mdpi.com/1420-3049/23/11/2830/s1: Energy interaction analysis for parametrized fragments, additional MEP, ESP, ELF/NCI, ELF populations and reaction path animations.

Author Contributions

E.A.V.-M. and G.A.C. conceived and designed the simulations; E.A.V.-M. performed the parametrization, MD and QM/MM geometry and path simulations, and ELF and NCI calculations; J.E.V.-C performed the geometry calculations in GP and DCM using SMD implicit solvent; E.A.V.-M., J.E.V.-C., and G.A.C. analyzed the data; and E.A.V.-M., J.E.V.-C., and G.A.C. wrote the paper.

Funding

This research was funded by CONACYT via a graduate fellowship to E.A.V.-M. and by NSF grant no. CHE-1531468 for CASCaM computing infrastructure.

Acknowledgments

The authors thank the UNT Department of Chemistry for the use of the HPC Cluster CRUNTCh3 and NSF Grant No. CHE–1531468. E.A.V.-M. wishes to acknowledge CONACyT for funding.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
ILIonic liquids
RTILRoom temperature ionic liquid
EMIm1–Ethyl–3–methylimidazolium
BF 4 Tetrafluoroborate
QMQuantum Mechanical
MMMolecular Mechanical
MDMolecular Dynamics
NPFFNon–polarizable force fields
PFFPolarizable force fields
GEMGaussian Electrostatic Model
TSTransition State
RCReaction Coordinate
GPGas–phase
DCMDichloromethane
ELFElectron Localization Function
NCINoncovalent Interaction
BFGSBroyden–Fletcher–Goldfarb–Shanno

References

  1. Walden, P. Molecular weights and electrical conductivity of several fused salts. Bull. Acad. Imp. Sci. (St. Petersburg) 1914, 8, 405–422. [Google Scholar]
  2. Plechkova, N.V.; Seddon, K.R. Applications of ionic liquids in the chemical industry. Chem. Soc. Rev. 2008, 37, 123–150. [Google Scholar] [CrossRef] [PubMed]
  3. Welton, T. Room-temperature ionic liquids. solvents for synthesis and catalysis. Chem. Rev. 1999, 99, 2071–2084. [Google Scholar] [CrossRef] [PubMed]
  4. Plechkova, N.V.; Rogers, R.D.; Seddon, K.R. Ionic liquids: From knowledge to application. J. Am. Chem. Soc. 2010, 132, 12518. [Google Scholar]
  5. Lipsztajn, M.; Osteryoung, R.A. Increased electrochemical window in ambient temperature neutral ionic liquids. J. Electrochem. Soc. 1983, 130, 1968–1969. [Google Scholar] [CrossRef]
  6. Wasserscheid, P.; Welton, T. (Eds.) Ionic Liquids in Synthesis, 2nd ed.; Wiley-VCH: Hoboken, NJ, USA, 2008. [Google Scholar]
  7. Erbeldinger, M.; Mesiano, A.J.; Russell, A.J. Enzymatic catalysis of formation of z-aspartame in ionic liquid—An alternative to enzymatic catalysis in organic solvents. Biotechnol. Prog. 2000, 16, 1129–1131. [Google Scholar] [CrossRef] [PubMed]
  8. Madeira Lau, R.; Van Rantwijk, F.; Seddon, K.R.; Sheldon, R.A. Lipase-catalyzed reactions in ionic liquids. Org. Lett. 2000, 2, 4189–4191. [Google Scholar] [CrossRef] [PubMed]
  9. Petkovic, M.; Seddon, K.R.; Rebelo, L.P.; Pereira, C.S. Ionic liquids: A pathway to environmental acceptability. Chem. Soc. Rev. 2011, 40, 1383–1403. [Google Scholar] [CrossRef] [PubMed]
  10. Hubbard, C.D.; Illner, P.; van Eldik, R. Understanding chemical reaction mechanisms in ionic liquids: Successes and challenges. Chem. Soc. Rev. 2011, 40, 272–290. [Google Scholar] [CrossRef] [PubMed]
  11. Hallett, J.P.; Welton, T. Room-Temperature Ionic Liquids: Solvents for Synthesis and Catalysis. 2. Chem. Rev. 2011, 111, 3508–3576. [Google Scholar] [CrossRef] [PubMed]
  12. Chiappe, C.; Malvaldi, M.; Pomelli, C.S. Ionic liquids: Solvation ability and polarity. Pure Appl. Chem. 2009, 81, 767–776. [Google Scholar] [CrossRef]
  13. Chiappe, C.; Pieraccini, D. Ionic liquids: Solvent properties and organic reactivity. J. Phys. Org. Chem. 2005, 18, 275–297. [Google Scholar] [CrossRef]
  14. Sarkar, A.; Roy, S.R.; Parikh, N.; Chakraborti, A.K. Nonsolvent application of ionic liquids: Organo-catalysis by 1-alkyl-3-methylimidazolium cation based room-temperature ionic liquids for chemoselective N-tert-butyloxycarbonylation of amines and the influence of the c-2 hydrogen on catalytic efficiency. J. Org. Chem. 2011, 76, 7132–7140. [Google Scholar] [CrossRef] [PubMed]
  15. Chankeshwara, S.V.; Chakraborti, A.K. Catalyst-free chemoselective N-tert-butyloxycarbonylation of amines in water. Org. Lett. 2006, 8, 3259–3262. [Google Scholar] [CrossRef] [PubMed]
  16. Ingale, A.P.; More, V.K.; Gangarde, U.S.; Shinde, S.V. Chemoselective N-tert-butyloxycarbonylation of amines in glycerol. New J. Chem. 2018, 42, 10142–10147. [Google Scholar] [CrossRef]
  17. Sambasivarao, S.V.; Acevedo, O. Development of OPLS-AA Force Field Parameters for 68 Unique Ionic Liquids. J. Chem. Theory Comput. 2009, 5, 1038–1050. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  18. Perez-Blanco, M.E.; Maginn, E.J. Molecular Dynamics Simulations of Carbon Dioxide and Water at an Ionic Liquid Interface. J. Phys. Chem. B 2011, 35, 10488–10499. [Google Scholar] [CrossRef] [PubMed]
  19. Maginn, E.J. Molecular simulation of ionic liquids: Current status and future opportunities. J. Phys. Condens. Matter 2009, 21, 373101. [Google Scholar] [CrossRef] [PubMed]
  20. Bhargava, B.L.; Balasubramanian, S.; Klein, M.L. Modelling room temperature ionic liquids. Chem. Commun. 2008, 29, 3339–3351. [Google Scholar] [CrossRef] [PubMed]
  21. Canongia Lopes, J.N.; Pádua, A.A. Using Spectroscopic Data on Imidazolium Cation Conformations to Test a Molecular Force Field for Ionic Liquids. J. Phys. Chem. B 2006, 110, 7485–7489. [Google Scholar] [CrossRef] [PubMed]
  22. Del Pópolo, M.G.; Lynden-Bell, R.M.; Kohanoff, J. Ab Initio Molecular Dynamics Simulation of a Room Temperature Ionic Liquid. J. Phys. Chem. B 2005, 109, 5895–5902. [Google Scholar] [CrossRef] [PubMed]
  23. Bhargava, B.L.; Balasubramanian, S. Dynamics in a room–temperature ionic liquid: A computer simulation study of 1,3-dimethylimidazolium chloride. J. Chem. Phys. 2005, 123, 144505. [Google Scholar] [CrossRef] [PubMed]
  24. Borodin, O.; Smith, G.D.; Kim, H. Viscosity of a Room Temperature Ionic Liquid: Predictions from Nonequilibrium and Equilibrium Molecular Dynamics Simulations. J. Phys. Chem. B 2009, 113, 4771–4774. [Google Scholar] [CrossRef] [PubMed]
  25. Borodin, O.; Smith, G.D. Development of Many–Body Polarizable Force Fields for Li–Battery Components: 1. Ether, Alkane, and Carbonate–Based Solvents. J. Phys. Chem. B 2006, 110, 6279–6292. [Google Scholar] [CrossRef] [PubMed]
  26. Schwörer, M.; Wichmann, C.; Tavan, P. A polarizable QM/MM approach to the molecular dynamics of amide groups solvated in water. J. Chem. Phys. 2016, 144, 114504. [Google Scholar] [CrossRef] [PubMed]
  27. Sneskov, K.; Schwabe, T.; Christiansen, O.; Kongsted, J. Scrutinizing the effects of polarization in QM/MM excited state calculations. Phys. Chem. Chem. Phys. 2011, 13, 18551. [Google Scholar] [CrossRef] [PubMed]
  28. Olsen, J.M.; Steinmann, C.; Ruud, K.; Kongsted, J. Polarizable Density Embedding: A New QM/QM/MM-Based Computational Strategy. J. Phys. Chem. A 2015, 119, 5344–5355. [Google Scholar] [CrossRef] [PubMed]
  29. Gao, J. Energy components of aqueous solution: Insight from hybrid QM/MM simulations using a polarizable solvent model. J. Comput. Chem. 1997, 18, 1061–1071. [Google Scholar] [CrossRef]
  30. Borodin, O. Polarizable Force Field Development and Molecular Dynamics Simulations of Ionic Liquids. J. Phys. Chem. B 2009, 113, 11463–11478. [Google Scholar] [CrossRef] [PubMed]
  31. Cisneros, G.A. Application of gaussian electrostatic model (gem) distributed multipoles in the amoeba force field. J. Chem. Theory Comput. 2012, 8, 5072–5080. [Google Scholar] [CrossRef] [PubMed]
  32. Starovoytov, O.N.; Torabifard, H.; Cisneros, G.A. Development of amoeba force field for 1,3-dimethylimidazolium based ionic liquids. J. Phys. Chem. B 2014, 118, 7156–7166. [Google Scholar] [CrossRef] [PubMed]
  33. Torabifard, H.; Starovoytov, O.N.; Ren, P.; Cisneros, G.A. Development of an amoeba water model using gem distributed multipoles. Theor. Chem. Acc. 2015, 134, 101. [Google Scholar] [CrossRef]
  34. Tu, Y.J.; Allen, M.J.; Cisneros, G.A. Simulations of the water exchange dynamics of lanthanide ions in 1-ethyl-3-methylimidazolium ethyl sulfate ([EMIm][EtSO4]) and water. Phys. Chem. Chem. Phys. 2016, 18, 30323–30333. [Google Scholar] [CrossRef] [PubMed]
  35. Tu, Y.J.; Lin, Z.; Allen, M.J.; Cisneros, G.A. Molecular Dynamics Investigation of Solvent–Exchange Reactions on Lanthanide Ions in Water/1-ethyl-3-methylimidazolium Trifuloromethylsulfate ([EMIm][OTf])) and water. J. Phys. Chem. 2018, 148, 024503. [Google Scholar] [CrossRef] [PubMed]
  36. Torabifard, H.; Reed, L.; Berry, M.T.; Hein, J.E.; Menke, E.; Cisneros, G.A. Computational and Experimental Characterization of a Pyrrolidinium–Based Ionic Liquid for Electrolyte Applications. J. Chem. Phys. 2017, 147, 161731. [Google Scholar] [CrossRef] [PubMed]
  37. Blanco-Díaz, E.G.; Vázquez-Montelongo, E.A.; Cisneros, G.A.; Castrejón-González, E.O. Computational investigation of non-covalent interactions in 1-butyl 3-methylimidazolium/bis(trifluoromethylsulfonyl)imide [BMIm][Tf2N] in EMD and NEMD. J. Chem. Phys. 2018, 148, 054303. [Google Scholar] [CrossRef] [PubMed]
  38. Ponder, J.W.; Wu, C.; Ren, P.; Pande, V.S.; Chodera, J.D.; Schnieders, M.J.; Haque, I.; Mobley, D.L.; Lambrecht, D.S.; DiStasio, R.A., Jr.; et al. Current status of the amoeba polarizable force field. J. Phys. Chem. B 2010, 114, 2549–2564. [Google Scholar] [CrossRef] [PubMed]
  39. Ren, P.; Ponder, J.W. Consistent treatment of inter- and intramolecular polarization in molecular mechanics calculations. J. Comput. Chem. 2002, 23, 1497–1506. [Google Scholar] [CrossRef] [PubMed]
  40. Ren, P.; Wu, C.; Ponder, J.W. Polarizable atomic multipole-based molecular mechanics for organic molecules. J. Chem. Theory Comput. 2011, 7, 3143–3161. [Google Scholar] [CrossRef] [PubMed]
  41. Cisneros, G.A.; Piquemal, J.P.; Darden, T.A. Quantum mechanics/molecular mechanics electrostatic embedding with continuous and discrete functions. J. Phys. Chem. B 2006, 110, 13682–13684. [Google Scholar] [CrossRef] [PubMed]
  42. Duke, R.E.; Starovoytov, O.N.; Piquemal, J.P.; Cisneros, G.A. Gem*: A molecular electronic density-based force field for molecular dynamics simulations. J. Chem. Theory Comput. 2014, 10, 1361–1365. [Google Scholar] [CrossRef] [PubMed]
  43. Piquemal, J.P.; Perera, L.; Cisneros, G.A.; Ren, P.; Pedersen, L.G.; Darden, T.A. Towards accurate solvation dynamics of divalent cations in water using the polarizable amoeba force field: From energetics to structure. J. Chem. Phys. 2006, 125, 054511. [Google Scholar] [CrossRef] [PubMed]
  44. Chiappe, C.; Pomelli, C.S. Computational studies on organic reactivity in ionic liquids. Phys. Chem. Chem. Phys. 2013, 15, 412–423. [Google Scholar] [CrossRef] [PubMed]
  45. Acevedo, O. Simulating Chemical Reactions in Ionic Liquids Using QM/MM Methodology. J. Phys. Chem. A 2014, 118, 11653–11666. [Google Scholar] [CrossRef] [PubMed]
  46. Acevedo, O.; Jorgensen, W.L. Advances in Quantum and Molecular Mechanical (QM/MM) Simulations for Organic and Enzymatic Reactions. Acc. Chem. Res. 2010, 43, 142–151. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  47. Acevedo, O.; Jorgensen, W.L.; Evanseck, J.D. Elucidation of Rate Variations for a Diels–Alder Reaction in Ionic Liquids from QM/MM Simulations. J. Chem. Theory Comput. 2007, 3, 132–138. [Google Scholar] [CrossRef] [PubMed]
  48. Allen, C.; Ghebreab, R.; Doherty, B.; Li, B.; Acevedo, O. Examining Ionic Liquid Effects on Mononuclear Rearrangement of Heterocycles Using QM/MM Simulations. J. Phys. Chem. B 2016, 120, 10786–10796. [Google Scholar] [CrossRef] [PubMed]
  49. Allen, C.; McCann, B.W.; Acevedo, O. Ionic Liquid Effects on Nucleophilic Aromatic Substitution Reactions from QM/MM Simulations. J. Phys. Chem. B 2015, 119, 743–752. [Google Scholar] [CrossRef] [PubMed]
  50. Allen, C.; Sambasivarao, S.V.; Acevedo, O. An Ionic Liquid Dependent Mechanism for Base Catalyzed β-Elimination Reactions from QM/MM Simulations. J. Am. Chem. Soc. 2013, 135, 1065–1072. [Google Scholar] [CrossRef] [PubMed]
  51. Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and testing of the opls all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
  52. Brooks, B.R.; Bruccoleri, R.E.; Olafson, B.D.; States, D.J.; Swaminathan, S.A.; Karplus, M. Charmm: A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 1983, 4, 187–217. [Google Scholar] [CrossRef]
  53. Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. Charmm general force field: A force field for drug-like molecules compatible with the charmm all-atom additive biological force fields. J. Comput. Chem. 2010, 31, 671–690. [Google Scholar] [CrossRef] [PubMed]
  54. Pearlman, D.A.; Case, D.A.; Caldwell, J.W.; Ross, W.S.; Cheatham, T.E., III; DeBolt, S.; Ferguson, D.; Seibel, G.; Kollman, P. Amber, a package of computer programs for applying molecular mechanics, normal mode analysis, molecular dynamics and free energy calculations to simulate the structural and energetic properties of molecules. Comput. Phys. Commun. 1995, 91, 1–41. [Google Scholar] [CrossRef]
  55. Lindorff-Larsen, K.; Piana, S.; Palmo, K.; Maragakis, P.; Klepeis, J.L.; Dror, R.O.; Shaw, D.E. Improved side-chain torsion potentials for the amber ff99sb protein force field. Proteins Struct. Funct. Bioinform. 2010, 78, 1950–1958. [Google Scholar] [CrossRef] [PubMed]
  56. Oostenbrink, C.; Villa, A.; Mark, A.E.; Van Gunsteren, W.F. A biomolecular force field based on the free enthalpy of hydration and solvation: The gromos force-field parameter sets 53a5 and 53a6. J. Comput. Chem. 2004, 25, 1656–1676. [Google Scholar] [CrossRef] [PubMed]
  57. Liu, M.Y.; Torabifard, H.; Crawford, D.J.; DeNizio, J.E.; Cao, X.J.; Garcia, B.A.; Cisneros, G.A.; Kohli, R.M. Mutations along a TET2 active site scaffold stall oxidation at 5-hydroxymethylcytosine. Nat. Chem. Biol. 2017, 13, 181–187. [Google Scholar] [CrossRef] [PubMed]
  58. Torabifard, H.; Cisneros, G.A. Insight into wild-type and T1372E TET2-mediated 5hmC oxidation using ab initio QM/MM calculations. Chem. Sci. 2018, 28–30. [Google Scholar] [CrossRef]
  59. Lu, X.; Fang, D.; Ito, S.; Okamoto, Y.; Ovchinnikov, V.; Cui, Q. QM/MM free energy simulations: Recent progress and challenges. Mol. Simul. 2016, 42, 1056–1078. [Google Scholar] [CrossRef] [PubMed]
  60. Roston, D.; Cui, Q. Chapter nine—QM/MM analysis of transition states and transition state analogues in metalloenzymes. In Methods in Enzymology; Voth, G.A., Ed.; Computational Approaches for Studying Enzyme Mechanism Part A; Academic Press: Cambridge, MA, USA, 2016; Volume 577, pp. 213–250. [Google Scholar]
  61. Vasilevskaya, T.; Khrenova, M.G.; Nemukhin, A.V.; Thiel, W. Methodological aspects of QM/MM calculations: A case study on matrix metalloproteinase-2. J. Comput. Chem. 2016, 37, 1801–1809. [Google Scholar] [CrossRef] [PubMed]
  62. Brunk, E.; Rothlisberger, U. Mixed Quantum Mechanical/Molecular Mechanical Molecular Dynamics Simulations of Biological Systems in Ground and Electronically Excited States. Chem. Rev. 2015, 115, 6217–6263. [Google Scholar] [CrossRef] [PubMed]
  63. Fang, D.; Cisneros, G.A. Alternative pathway for the reaction catalyzed by DNA dealkylase AlkB from Ab initio QM/MM calculations. J. Chem. Theory Comput. 2014, 10, 5136–5148. [Google Scholar] [CrossRef] [PubMed]
  64. Fang, D.; Lord, R.L.; Cisneros, G.A. Ab Initio QM/MM Calculations Show an Intersystem Crossing in the Hydrogen Abstraction Step in Dealkylation Catalyzed by AlkB. J. Phys. Chem. B 2013, 117, 6410–6420. [Google Scholar] [CrossRef] [PubMed]
  65. Acevedo, O.; Armacost, K. Claisen Rearrangements: Insight into Solvent Effects and “on Water” Reactivity from QM/MM Simulations. J. Am. Chem. Soc. 2010, 132, 1966–1975. [Google Scholar] [CrossRef] [PubMed]
  66. Senn, H.M.; Thiel, W. QM/MM Methods for Biomolecular Systems. Angew. Chem. Int. Ed. 2009, 48, 1198–1229. [Google Scholar] [CrossRef] [PubMed]
  67. Parks, J.M.; Hu, H.; Rudolph, J.; Yang, W. Mechanism of Cdc25B Phosphatase with the Small Molecule Substrate p-Nitrophenyl Phosphate from QM/MM-MFEP Calculations. J. Phys. Chem. B 2009, 113, 5217–5224. [Google Scholar] [CrossRef] [PubMed]
  68. Hu, H.; Lu, Z.; Parks, J.M.; Burger, S.K.; Yang, W. Quantum mechanics/molecular mechanics minimum free-energy path for accurate reaction energetics in solution and enzymes: Sequential sampling and optimization on the potential of mean force surface. J. Chem. Phys. 2008, 128, 034105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  69. Hu, H.; Lu, Z.; Yang, W. QM/MM Minimum Free-Energy Path: Methodology and Application to Triosephosphate Isomerase. J. Chem. Theory Comput. 2007, 3, 390–406. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  70. Tubert-Brohman, I.; Acevedo, O.; Jorgensen, W.L. Elucidation of Hydrolysis Mechanisms for Fatty Acid Amide Hydrolase and Its Lys142Ala Variant via QM/MM Simulations. J. Am. Chem. Soc. 2006, 128, 16904–16913. [Google Scholar] [CrossRef] [PubMed]
  71. Acevedo, O.; Jorgensen, W.L. Medium Effects on the Decarboxylation of a Biotin Model in Pure and Mixed Solvents from QM/MM Simulations. J. Org. Chem. 2006, 71, 4896–4902. [Google Scholar] [CrossRef] [PubMed]
  72. Cisneros, G.A.; Liu, H.; Lu, Z.; Yang, W. Reaction path determination for quantum mechanical/molecular mechanical modeling of enzyme reactions by combining first order and second order “chain-of-replicas” methods. J. Chem. Phys. 2005, 122, 114502. [Google Scholar] [CrossRef] [PubMed]
  73. Heyden, A.; Lin, H.; Truhlar, D.G. Adaptive partitioning in combined quantum mechanical and molecular mechanical calculations of potential energy functions for multiscale simulations. J. Phys. Chem. B 2007, 111, 2231–2241. [Google Scholar] [CrossRef] [PubMed]
  74. Duster, A.W.; Wang, C.H.; Garza, C.M.; Miller, D.E.; Lin, H. Adaptive quantum/molecular mechanics: What have we learned, where are we, and where do we go from here? Wiley Interdiscip. Rev. Comput. Mol. Sci. 2017, 7, e1310. [Google Scholar] [CrossRef]
  75. Gao, J.; Alhambra, C. A hybrid semiempirical quantum mechanical and lattice–sum method for electrostatic interactions in fluid simulations. J. Chem. Phys. 1997, 107, 1212–1217. [Google Scholar] [CrossRef]
  76. Slipchenko, L.V. Solvation of the excited states of chromophores in polarizable environment: Orbital relaxation versus polarization. J. Phys. Chem. A 2010, 114, 8824–8830. [Google Scholar] [CrossRef] [PubMed]
  77. Giese, T.J.; York, D.M. Charge-dependent model for many-body polarization, exchange, and dispersion interactions in hybrid quantum mechanical/molecular mechanical calculations. J. Chem. Phys. 2007, 127, 194101. [Google Scholar] [CrossRef] [PubMed]
  78. Illingworth, C.J.; Parkes, K.E.; Snell, C.R.; Marti, S.; Moliner, V.; Reynolds, C.A. The effect of mm polarization on the qm/mm transition state stabilization: Application to chorismate mutase. Mol. Phys. 2008, 106, 1511–1515. [Google Scholar] [CrossRef]
  79. Boulanger, E.; Thiel, W. Solvent boundary potentials for hybrid qm/mm computations using classical drude oscillators: A fully polarizable model. J. Chem. Theory Comput. 2012, 8, 4527–4538. [Google Scholar] [CrossRef] [PubMed]
  80. Nakano, H.; Yamamoto, T. Variational calculation of quantum mechanical/molecular mechanical free energy with electronic polarization of solvent. J. Chem. Phys. 2012, 136, 134107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  81. Kratz, E.G.; Walker, A.R.; Lagardère, L.; Lipparini, F.; Piquemal, J.P.; Andrés Cisneros, G. Lichem: A qm/mm program for simulations with multipolar and polarizable force fields. J. Comput. Chem. 2016, 37, 1019–1029. [Google Scholar] [CrossRef] [PubMed]
  82. Carey, J.S.; Laffan, D.; Thomson, C.; Williams, M.T. Analysis of the reactions used for the preparation of drug candidate molecules. Org. Biomol. Chem. 2006, 4, 2337–2347. [Google Scholar] [CrossRef] [PubMed]
  83. Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
  84. Silvi, B.; Savin, A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature 1994, 371, 683–686. [Google Scholar] [CrossRef]
  85. Silvi, B. How topological partitions of the electron distributions reveal delocalization. Phys. Chem. Chem. Phys. 2004, 6, 256–260. [Google Scholar] [CrossRef]
  86. Johnson, E.R.; Keinan, S.; Mori-Sanchez, P.; Contreras-Garcia, J.; Cohen, A.J.; Yang, W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  87. Contreras-García, J.; Johnson, E.R.; Keinan, S.; Chaudret, R.; Piquemal, J.P.; Beratan, D.N.; Yang, W. NCIPLOT: A Program for Plotting Noncovalent Interaction Regions. J. Chem. Theory Comput. 2011, 7, 625–632. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  88. Gillet, N.; Chaudret, R.; Contreras-García, J.; Yang, W.; Silvi, B.; Piquemal, J.P. Coupling Quantum Interpretative Techniques: Another Look at Chemical Mechanisms in Organic Reactions. J. Chem. Theory Comput. 2012, 8, 3993–3997. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  89. Chaudret, R.; Piquemal, J.P.; Cisneros, G.A. Correlation between electron localization and metal ion mutagenicity in DNA synthesis from QM/MM calculations. Phys. Chem. Chem. Phys. 2011, 13, 11239. [Google Scholar] [CrossRef] [PubMed]
  90. Fang, D.; Chaudret, R.; Piquemal, J.P.; Cisneros, G.A. Toward a Deeper Understanding of Enzyme Reactions Using the Coupled ELF/NCI Analysis: Application to DNA Repair Enzymes. J. Chem. Theory Comput. 2013, 9, 2156–2160. [Google Scholar] [CrossRef] [PubMed]
  91. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R. Gaussian09 Revision E.01, Gaussian Inc.: Wallingford, CT, USA, 2009.
  92. Parrish, R.M.; Burns, L.A.; Smith, D.G.; Simmonett, A.C.; DePrince, A.E., III; Hohenstein, E.G.; Bozkaya, U.; Sokolov, A.Y.; Di Remigio, R.; Richard, R.M.; et al. Psi4 1.1: An open-source electronic structure program emphasizing automation, advanced libraries, and interoperability. J. Chem. Theory Comput. 2017, 13, 3185–3197. [Google Scholar] [CrossRef] [PubMed]
  93. Harger, M.; Li, D.; Wang, Z.; Dalby, K.; Lagardère, L.; Piquemal, J.P.; Ponder, J.; Ren, P. Tinker-openmm: Absolute and relative alchemical free energies using amoeba on gpus. J. Comput. Chem. 2017, 38, 2047–2055. [Google Scholar] [CrossRef] [PubMed]
  94. Chai, J.D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed]
  95. Ditchfield, R.H.; Hehre, W.J.; Pople, J.A. Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules. J. Chem. Phys. 1971, 54, 724–728. [Google Scholar] [CrossRef]
  96. Peng, C.; Bernhard Schlegel, H. Combining synchronous transit and quasi-newton methods to find transition states. Isr. J. Chem. 2000, 33, 449–454. [Google Scholar] [CrossRef]
  97. Fang, D.; Duke, R.E.; Cisneros, G.A. A new smoothing function to introduce long-range electrostatic effects in QM/MM calculations. J. Chem. Phys. 2015, 143, 044103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  98. Kratz, E.G.; Duke, R.E.; Cisneros, G.A. Long-range electrostatic corrections in multipolar/polarizable qm/mm simulations. Theor. Chem. Acc. 2016, 135, 166. [Google Scholar] [CrossRef] [PubMed]
  99. Henkelman, G.; Uberuaga, B.P.; Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef]
  100. Burger, S.K.; Yang, W. Quadratic string method for determining the minimum-energy path based on multiobjective optimization. J. Chem. Phys. 2006, 124, 054109. [Google Scholar] [CrossRef] [PubMed]
  101. Cisneros, G.A.; Yang, W. Comparison of reaction barriers in energy and free energy for enzyme catalysis. In Multi-Scale Quantum Models for Biocatalysis: Modern Techniques and Applications; York, D.M., Lee, T.-S., Eds.; Springer: Dordrecht, The Netherlands, 2009; pp. 57–78. [Google Scholar]
  102. Gokcan, H.; Vazquez-Montelongo, E.A.; Cisneros, G.A. LICHEM 1.1: Recent Improvements and New Capabilities. J. Mex. Chem. Soc. 2018. submitted. [Google Scholar]
  103. Noury, S.; Krokidis, X.; Fuster, F.; Silvi, B. Computational tools for the electron localization function topological analysis. Comput. Chem. 1999, 23, 597–604. [Google Scholar] [CrossRef]
  104. Pilmé, J.; Piquemal, J.P. Advancing beyond charge analysis using the electronic localization function: Chemically intuitive distribution of electrostatic moments. J. Comput. Chem. 2008, 29, 1440–1449. [Google Scholar] [CrossRef] [PubMed]
  105. Stone, A.J. Distributed multipole analysis, or how to describe a molecular charge distribution. Chem. Phys. Lett. 1981, 83, 233–239. [Google Scholar] [CrossRef]
  106. Torabifard, H.; Cisneros, G.A. Computational investigation of O2 diffusion through an intra-molecular tunnel in AlkB; influence of polarization on O2 transport. Chem. Sci. 2017, 8, 6230–6238. [Google Scholar] [CrossRef] [PubMed]
Molecules 23 02830 g001 550
Figure 1. Intermolecular Coulomb interaction for the set of randomly oriented aniline/water (left) and [(Boc) 2 O]/water (right) dimers.
Figure 1. Intermolecular Coulomb interaction for the set of randomly oriented aniline/water (left) and [(Boc) 2 O]/water (right) dimers.
Molecules 23 02830 g001
Molecules 23 02830 sch001 550
Scheme 1. Reaction scheme for the N- t e r t -Butyloxycarbonylation of aniline. Panels (a,b) show the activation of (Boc) 2 O through bifurcated hydrogen bond formation between the water molecule or the IL cation ([EMIM] + ). Panel (c) corresponds to a sequential reaction mechanism without (Boc) 2 O activation. Panel (d) also corresponds to a concerted mechanism.
Scheme 1. Reaction scheme for the N- t e r t -Butyloxycarbonylation of aniline. Panels (a,b) show the activation of (Boc) 2 O through bifurcated hydrogen bond formation between the water molecule or the IL cation ([EMIM] + ). Panel (c) corresponds to a sequential reaction mechanism without (Boc) 2 O activation. Panel (d) also corresponds to a concerted mechanism.
Molecules 23 02830 sch001
Molecules 23 02830 g002 550
Figure 2. Comparison between the relative distance the reactants and [EMIM][BF 4 ]. (a) Molecular dynamics (MD) with restrain distance between reactants and [EMIM][BF 4 ]. (b) MD without restrain distance between reactants and [EMIM][BF 4 ]. Where colors correspond to: C–gray, O–red, N–blue, H–white, B–pink, F–cyan.
Figure 2. Comparison between the relative distance the reactants and [EMIM][BF 4 ]. (a) Molecular dynamics (MD) with restrain distance between reactants and [EMIM][BF 4 ]. (b) MD without restrain distance between reactants and [EMIM][BF 4 ]. Where colors correspond to: C–gray, O–red, N–blue, H–white, B–pink, F–cyan.
Molecules 23 02830 g002
Molecules 23 02830 g003 550
Figure 3. Minimum energy path for Configuration C1, Scheme 1c.
Figure 3. Minimum energy path for Configuration C1, Scheme 1c.
Molecules 23 02830 g003
Molecules 23 02830 g004 550
Figure 4. Minimum energy path for Configuration C2, Scheme 1c.
Figure 4. Minimum energy path for Configuration C2, Scheme 1c.
Molecules 23 02830 g004
Molecules 23 02830 g005 550
Figure 5. Minimum energy path for Configuration C2, Scheme 1d.
Figure 5. Minimum energy path for Configuration C2, Scheme 1d.
Molecules 23 02830 g005
Molecules 23 02830 g006 550
Figure 6. Energy profile for Scheme 1c for gas phase (GP) and dichloromethane (DCM). The figure shows the reaction energy and reaction barrier in the gas phase (red), and with DCM using the SMD implicit solvent model (green).
Figure 6. Energy profile for Scheme 1c for gas phase (GP) and dichloromethane (DCM). The figure shows the reaction energy and reaction barrier in the gas phase (red), and with DCM using the SMD implicit solvent model (green).
Molecules 23 02830 g006
Molecules 23 02830 g007 550
Figure 7. Atom labeling for Merz–Singh–Kollman (ESP) and electron localization function (ELF)/noncovalent interaction (NCI) analysis. Atom coloring is same as in Figure 2.
Figure 7. Atom labeling for Merz–Singh–Kollman (ESP) and electron localization function (ELF)/noncovalent interaction (NCI) analysis. Atom coloring is same as in Figure 2.
Molecules 23 02830 g007
Molecules 23 02830 g008 550
Figure 8. ESP charges for the atoms involved in the MEP for Scheme 1c (right) and d left) for Configuration C2.
Figure 8. ESP charges for the atoms involved in the MEP for Scheme 1c (right) and d left) for Configuration C2.
Molecules 23 02830 g008
Molecules 23 02830 g009 550
Figure 9. Combined ELF/NCI surfaces for the TS structures for the rate-limiting step in Scheme 1c. (a) GP, (b) DCM, (c) Configuration C1, (d) Configuration C2. The isovalue for ELF was 0.83, and for NCI it was 0.5, with a color scale of −0.05 au < sign( λ 2) ρ < 0.05 au.
Figure 9. Combined ELF/NCI surfaces for the TS structures for the rate-limiting step in Scheme 1c. (a) GP, (b) DCM, (c) Configuration C1, (d) Configuration C2. The isovalue for ELF was 0.83, and for NCI it was 0.5, with a color scale of −0.05 au < sign( λ 2) ρ < 0.05 au.
Molecules 23 02830 g009
Molecules 23 02830 g010 550
Figure 10. Combined ELF/NCI surfaces of the critical structures for Configuration C2 for Scheme 1d. Panels (a–e) show the reactants, TS1, MI, TS2, and products structures, respectively. The isovalue for ELF was 0.83 and for NCI was 0.5, with a color scale of −0.05 au < sign( λ 2) ρ < 0.05 au.
Figure 10. Combined ELF/NCI surfaces of the critical structures for Configuration C2 for Scheme 1d. Panels (a–e) show the reactants, TS1, MI, TS2, and products structures, respectively. The isovalue for ELF was 0.83 and for NCI was 0.5, with a color scale of −0.05 au < sign( λ 2) ρ < 0.05 au.
Molecules 23 02830 g010
Molecules 23 02830 g011 550
Figure 11. Minimum energy path for Scheme 1c (right) and d (left) for Configuration C2 without the AMOEBA polarization term.
Figure 11. Minimum energy path for Scheme 1c (right) and d (left) for Configuration C2 without the AMOEBA polarization term.
Molecules 23 02830 g011
Table
Table 1. Quantum-mechanics/molecular-mechanics (QM/MM) reaction energies (kcal/mol) corresponding to Scheme 1.
Table 1. Quantum-mechanics/molecular-mechanics (QM/MM) reaction energies (kcal/mol) corresponding to Scheme 1.
MechanismConfiguration C1Configuration C2
a114.4627.42
b174.51–
c−27.93−20.88
d−21.86−20.14
Table
Table 2. ESP charges for selected atoms for the reaction in DCM(GP) for Scheme 1c.
Table 2. ESP charges for selected atoms for the reaction in DCM(GP) for Scheme 1c.
AtomReactantTransition StateProduct
C(1)0.90(0.89)0.92(1.02)0.93(0.93)
O(13)−0.45(−0.45)−0.66(−0.66)−0.60(−0.60)
N(43)−0.95(−0.94)−0.76(−0.76)−0.79(−0.78)
H(44)0.39(0.39)0.42(0.43)0.40(00.39)
H(45)0.38(0.38)0.41(0.41)0.43(00.44)
Table
Table 3. ELF population (pop.) analysis for TS structures for the reaction in the GP, DCM, and Configurations C1 and C2 for Scheme 1c.
Table 3. ELF population (pop.) analysis for TS structures for the reaction in the GP, DCM, and Configurations C1 and C2 for Scheme 1c.
BasinGP Pop.DCM Pop.C1 TS1 Pop.C2 TS1 Pop.C2 TS2 Pop.
V(H44,N43)2.262.242.162.212.17
V(H45,N43)2.342.332.482.24–
V(C1,O15)1.791.731.691.611.87
V(C1,O14)2.502.302.212.002.37
V(C1,O13)––1.231.20–
V(C6,O13)2.142.131.891.842.17
V(C6,O12)2.682.652.572.642.44
V(C1,N43)2.062.072.542.812.06
V(H45)––––0.51
Table
Table 4. ELF populations and first polar moment ( μ ) analysis for specific basins involved in the reaction in the water/IL mixture corresponding to Configuration C2, Scheme 1d.
Table 4. ELF populations and first polar moment ( μ ) analysis for specific basins involved in the reaction in the water/IL mixture corresponding to Configuration C2, Scheme 1d.
Basin1st TSMI2nd TS
Pop. μ (au)Pop. μ (au)Pop. μ (au)
V(H44,N43)2.241.8692.181.7652.161.64
V(H45,N43)2.311.8172.181.756––
V(H45,O11)––––1.641.35
V(C1,O15)1.860.081.930.0731.840.041
V(C1,O14)2.460.7262.40.552.270.237
V(C1,O13)1.230.319––––
V(C1,N43)––2.000.1482.61.085
V(C6,O13)1.670.0692.090.2422.390.577
V(C6,O12)2.390.6452.130.2392.240.393
V(C6,O11)1.810.0191.580.0611.180.294

Share and Cite

MDPI and ACS Style

Vázquez-Montelongo, E.A.; Vázquez-Cervantes, J.E.; Cisneros, G.A. Polarizable ab initio QM/MM Study of the Reaction Mechanism of N-tert-Butyloxycarbonylation of Aniline in [EMIm][BF4]. Molecules 2018, 23, 2830. https://doi.org/10.3390/molecules23112830

AMA Style

Vázquez-Montelongo EA, Vázquez-Cervantes JE, Cisneros GA. Polarizable ab initio QM/MM Study of the Reaction Mechanism of N-tert-Butyloxycarbonylation of Aniline in [EMIm][BF4]. Molecules. 2018; 23(11):2830. https://doi.org/10.3390/molecules23112830

Chicago/Turabian Style

Vázquez-Montelongo, Erik Antonio, José Enrique Vázquez-Cervantes, and G. Andrés Cisneros. 2018. "Polarizable ab initio QM/MM Study of the Reaction Mechanism of N-tert-Butyloxycarbonylation of Aniline in [EMIm][BF4]" Molecules 23, no. 11: 2830. https://doi.org/10.3390/molecules23112830

APA Style

Vázquez-Montelongo, E. A., Vázquez-Cervantes, J. E., & Cisneros, G. A. (2018). Polarizable ab initio QM/MM Study of the Reaction Mechanism of N-tert-Butyloxycarbonylation of Aniline in [EMIm][BF4]. Molecules, 23(11), 2830. https://doi.org/10.3390/molecules23112830

Article Metrics

Back to TopTop