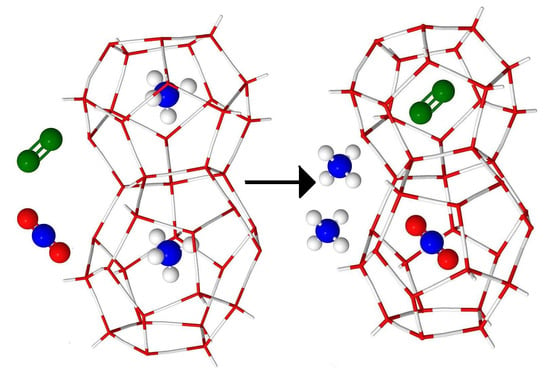
Influence of N2 on Formation Conditions and Guest Distribution of Mixed CO2 + CH4 Gas Hydrates
Abstract
:1. Introduction
2. Methods
2.1. Implemented Theoretical Models
- (a)
- For binary clathrate hydrates with cavities of two types including two types of guest molecules and the possibility of single occupancy for type guests and single occupancy for type guests of both the small and large cavities, , , ; is the part of free energy at a given degree of filling of the guest molecules in the and cavities; , are filling degrees for cavities of the th type () by guest molecules of the th type (); is the number of cavities of the th type; and is the number of guest molecules of the th type contained in cavities of the th type.
- (b)
- For ternary clathrate hydrates with cavities of two types including three types of guest molecules and the possibility of single occupancy for type guests and single occupancy for type guests of both the small and large cavities, as well as the possibility of single occupancy for type guests of the small and multiple occupancy large cavities, , , , , ; is the part of free energy at a given degree of filling of the guest molecules in the and cavities; , is the filling degree for a cavity of the th type () by guest molecules of the th type (); is the number of cavities of the th type; is the number of guest molecules of the th type contained in cavities of the th type.
2.2. Simulations Details
3. Results and Discussion
3.1. Gas–Hydrate Phase Equilibria
3.2.Gas–Hydrate–Ice (Water)Phase Equilibria
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Marchetti, C. On geoengineering and the CO2 problem. Clim. Chang. 1977, 1, 59–68. Available online: https://link.springer.com/article/10.1007/BF00162777 (accessed on 13 December 2018). [CrossRef]
- Stevens, S.H.; Kuuskraa, V.A.; Gale, J.; Beecy, D. CO2 injection and sequestration in depleted oil and gas fields and deep coal seams: Worldwide potential and costs. Environ. Geosci. 2001, 8, 200–209. [Google Scholar] [CrossRef]
- Ohgaki, K. Proposal for gas storage on the ocean floor using gas hydrate. Kagaku Kogaku Ronbunshu 1991, 17, 1053–1055. [Google Scholar] [CrossRef]
- House, K.Z.; Schrag, D.P.; Harvey, C.F.; Lackner, K.S. Permanent carbon dioxide storage in deep-sea sediments. Proc. Nat. Acad. Sci. USA 2006, 103, 12291–12295. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stern, L.A.; Kirby, S.H.; Durham, W.B. Peculiarities of methane clathrate hydrate formation and solid-state deformation, including possible superheating of water ice. Science 1996, 273, 1843–1848. [Google Scholar] [CrossRef]
- Sloan, E.D., Jr.; Koh, C. Clathrate Hydrates of Natural Gases, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2007; pp. 1–752. [Google Scholar]
- Lee, H.; Seo, Y.; Seo, Y.T.; Moudrakovski, I.L.; Ripmeester, J.A. Recovering methane from solid methane hydrate with carbon dioxide. Angew. Chem. Int. Ed. 2003, 42, 5048–5051. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.; Kim, D.Y.; Lee, J.W.; Huh, D.G.; Park, K.P.; Lee, J.; Lee, H. Sequestering carbon dioxide into complex structures of naturally occurring gas hydrates. Proc. Nat. Acad. Sci. USA 2006, 103, 12690–12694. [Google Scholar] [CrossRef] [Green Version]
- Shin, K.; Park, Y.; Cha, M.; Park, K.P.; Huh, D.G.; Lee, J.; Lee, H. Swapping phenomena occurring in deep-sea gas hydrates. Energy Fuel 2008, 22, 3160–3163. [Google Scholar] [CrossRef]
- Brewer, P.G.; Friederich, G.; Peltzer, E.T.; Orr, F.M. Direct experiments on the ocean disposal of fossil fuel CO2. Science 1999, 284, 943–945. [Google Scholar] [CrossRef] [PubMed]
- Koh, D.Y.; Kang, H.; Kim, D.O.; Park, J.; Cha, M.; Lee, H. Recovery of methane from gas hydrates intercalated within natural sediments using CO2 and a CO2/N2 gas mixture. ChemSusChem 2012, 5, 1443–1448. [Google Scholar] [CrossRef]
- Kvamme, B.; Graue, A.; Buanes, T.; Kuznetsova, T.; Ersland, G. Storage of CO2 in natural gas hydrate reservoirs and the effect of hydrate as an extra sealing in cold aquifers. Int. J. Greenh. Gas Con. 2007, 1, 236–246. [Google Scholar] [CrossRef]
- Seo, Y.T.; Lee, H. Multiple-phase hydrate equilibria of the ternary carbon dioxide, methane, and water mixtures. J. Phys. Chem. B 2001, 105, 10084–10090. [Google Scholar] [CrossRef]
- Belosludov, V.R.; Subbotin, O.S.; Belosludov, R.V.; Mizuseki, H.; Kawazoe, Y. Thermodynamic phase behavior of binary clathrate hydrates: Computational prediction. Comput. Mater. Sci. 2010, 49, S187–S193. [Google Scholar] [CrossRef]
- Adamova, T.P.; Subbotin, O.S.; Pomeransky, A.A.; Belosludov, V.R. Modeling of phase transition sI−sII in binary gas hydrates of methane and ethane in dependence on composition of gas phase. Comput. Mater. Sci. 2010, 9, S317–S321. [Google Scholar] [CrossRef]
- Tung, Y.T.; Chen, L.J.; Chen, Y.P.; Lin, S.T. In situ methane recovery and carbon dioxide sequestration in methane hydrates: A molecular dynamics simulation study. J. Phys. Chem. B 2011, 115, 15295–15302. [Google Scholar] [CrossRef] [PubMed]
- Belosludov, R.V.; Zhdanov, R.K.; Subbotin, O.S.; Mizuseki, H.; Souissi, M.; Kawazoe, Y.; Belosludov, V.R. Theoretical modelling of the phase diagrams of clathrate hydrates for hydrogen storage applications. Mol. Simulat. 2012, 38, 773–780. [Google Scholar] [CrossRef]
- Bozhko, Y.Y.; Subbotin, O.S.; Gets, K.V.; Zhdanov, R.K.; Belosludov, V.R. Theoretical modeling of the gas hydrates of nitrous oxide and methane mixtures. Mendeleev Commun. 2017, 27, 397–398. [Google Scholar] [CrossRef]
- Zhdanov, R.K.; Gets, K.V.; Belosludov, R.V.; Subbotin, O.S.; Bozhko, Y.Y.; Belosludov, V.R. Theoretical modeling of the thermodynamic properties and the phase diagram of binary gas hydrates of argon and hydrogen. Fluid Phase Equilibria 2017, 434, 87–92. [Google Scholar] [CrossRef]
- Belosludov, R.V.; Zhdanov, R.K.; Subbotin, O.S.; Mizuseki, H.; Kawazoe, Y.; Belosludov, V.R. Theoretical study of hydrogen storage in binary hydrogen-methane clathrate hydrates. J. Renew. Sust. Energy 2014, 6, 053132. [Google Scholar] [CrossRef]
- Bozhko, Y.Y.; Subbotin, O.S.; Fomin, V.M.; Belosludov, V.R.; Kawazoe, Y. Theoretical investigation of structures, compositions, and phase transitions of neon hydrates based on ices Ih and II. J. Eng. Thermophys. 2014, 23, 20–26. [Google Scholar] [CrossRef]
- Belosludov, R.V.; Subbotin, O.S.; Mizuseki, H.; Kawazoe, Y.; Belosludov, V.R. Accurate description of phase diagram of clathrate hydrates at the molecular level. J. Phys. Chem. 2009, 131, 244510. [Google Scholar] [CrossRef]
- Seo, Y.T.; Lee, H.; Yoon, J.H. Hydrate phase equilibria of the carbon dioxide, methane, and water system. J. Chem. Eng. Data 2001, 46, 381–384. [Google Scholar] [CrossRef]
- Belandria, V.; Mohammadi, A.H.; Richon, D. Phase equilibria of clathrate hydrates of methane + carbon dioxide: New experimental data and predictions. Fluid Phase Equilibria 2010, 296, 60–65. [Google Scholar] [CrossRef]
- Kang, S.P.; Lee, H.; Lee, C.S.; Sung, W.M. Hydrate phase equilibria of the guest mixtures containing CO2, N2 and tetrahydrofuran. Fluid Phase Equilibria 2001, 185, 101–109. [Google Scholar] [CrossRef]
- Seo, Y.T.; Moudrakovski, I.L.; Ripmeester, J.A.; Lee, J.W.; Lee, H. Efficient recovery of CO2 from flue gas by clathrate hydrate formation in porous silica gels. Environ. Sci. Technol. 2005, 39, 2315–2319. [Google Scholar] [CrossRef] [PubMed]
- Seo, Y.T.; Lee, H. Structure and guest distribution of the mixed carbon dioxide and nitrogen hydrates as revealed by X-ray diffraction and 13C-NMR spectroscopy. J. Phys. Chem. B 2004, 108, 530–534. [Google Scholar] [CrossRef]
- Seo, Y.T.; Lee, H.; Uchida, T. Methane and carbon dioxide hydrate phase behavior in small porous silica gels: Three-phase equilibrium determination and thermodynamic modeling. Langmuir 2002, 18, 9164–9170. [Google Scholar] [CrossRef]
- Waals, J.V.D.; Platteeuw, J.C. Clathrate solutions. Adv. Chem. Phys. 1959, 2, 1–58. [Google Scholar]
- Kuhs, W.F.; Chazallon, B.; Radaelli, P.G.; Pauer, F. Cage occupancy and compressibility of deuterated N2-clathrate hydrate by neutron diffraction. J. Incl. Phenom. Macrocycl. Chem. 1997, 29, 65–77. [Google Scholar] [CrossRef]
- Chazallon, B.; Kuhs, W.F. In situ structural properties of N2−, O2−, and air-clathrates by neutron diffraction. J. Chem. Phys. 2002, 117, 308–320. [Google Scholar] [CrossRef]
- Van Klaveren, E.P.; Michels, J.P.J.; Schouten, J.A.; Klug, D.D.; Tse, J.S. Stability of doubly occupied N2 clathrate hydrates investigated by molecular dynamics simulations. J. Chem. Phys. 2001, 114, 5745–5754. [Google Scholar] [CrossRef]
- van Klaveren, E.P.; Michels, J.P.J.; Schouten, J.A.; Klug, D.D.; Tse, J.S. Molecular dynamics simulation study of the properties of doubly occupied N2 clathrate hydrates. J. Chem. Phys. 2001, 115, 10500–10508. [Google Scholar] [CrossRef]
- Belosludov, V.R.; Subbotin, O.S.; Krupskii, D.S.; Belosludov, R.V.; Kawazoe, Y.; Kudoh, J.I. Physical and chemical properties of gas hydrates: Theoretical aspects of energy storage application. Mater. Trans. 2007, 48, 704–710. [Google Scholar] [CrossRef]
- Subbotin, O.S.; Adamova, T.P.; Belosludov, R.V.; Mizuseki, H.; Kawazoe, Y.; Kudoh, J.I.; Belosludov, V.R. Theoretical study of phase transitions in Kr and Ar clathrate hydrates from structure II to structure I under pressure. J. Chem. Phys. 2009, 131, 114507. [Google Scholar] [CrossRef]
- Souissi, M.; Belosludov, R.V.; Subbotin, O.S.; Mizuseki, H.; Kawazoe, Y.; Belosludov, V.R. Thermodynamic stability of C3H8 hydrate of cubic structure IV using lattice dynamics. J. Incl. Phenom. Macrocycl. Chem. 2011, 69, 281–286. [Google Scholar] [CrossRef]
- Belosludov, R.V.; Bozhko, Y.Y.; Subbotin, O.S.; Belosludov, V.R.; Mizuseki, H.; Kawazoe, Y.; Fomin, V.M. Stability and composition of helium hydrates based on ices Ih and II at low temperatures. J. Phys. Chem. C 2014, 118, 2587–2593. [Google Scholar] [CrossRef]
- Bozhko, Y.Y.; Subbotin, O.S.; Fomin, V.M.; Belosludov, V.R.; Kawazoe, Y. Theoretical investigation of structures and compositions of double neon-methane clathrate hydrates, depending on gas phase composition and pressure. J. Eng. Thermophys. 2014, 23, 9–19. [Google Scholar] [CrossRef]
- Jager, M.D.; Ballard, A.L.; Sloan, E.D., Jr. The next generation of hydrate prediction: II. dedicated aqueous phase fugacity model for hydrate prediction. Fluid Phase Equilibria 2003, 211, 85–107. [Google Scholar] [CrossRef]
- Bernal, J.D.; Fowler, R.H. A theory of water and ionic solution, with particular reference to hydrogen and hydroxyl ions. J. Chem. Phys. 1933, 1, 515–548. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Grigera, J.R.; Straatsma, T.P. The missing term in effective pair potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Martin, M.G.; Siepmann, J.I. Transferable potentials for phase equilibria. 1. United-atom description of n-alkanes. J. Phys. Chem. B 1998, 102, 2569–2577. [Google Scholar] [CrossRef]
- Fomin, V.V. NASA Technical Memorandum NASA TM-75655. Available online: https://ntrs.nasa.gov/search.jsp?R=19790021554 (accessed on 13 December 2018).
- Vishnyakov, A.; Debenedetti, P.G.; Neimark, A.V. Statistical geometry of cavities in a metastable confined fluid. Phys. Rev. E 2000, 62, 538. [Google Scholar] [CrossRef]
- Zhdanov, R.K.; Adamova, T.P.; Subbotin, O.S.; Pomeranskii, A.A.; Belosludov, V.R.; Dontsov, V.R.; Nakoryakov, V.E. Modeling the properties of methane + ethane (Propane) binary hydrates, depending on the composition of gas phase state in equilibrium with hydrate. J. Eng. Thermophys. 2010, 19, 282–288. [Google Scholar] [CrossRef]
- Subbotin, O.S.; Bozhko, Y.Y.; Zhdanov, R.K.; Gets, K.V.; Belosludov, V.R.; Belosludov, R.V.; Kawazoe, Y. Ozone storage capacity in clathrate hydrates formed by O3+ O2+ N2+ CO2 gas mixtures. Phys. Chem. Chem. Phys. 2018, 20, 12637–12641. [Google Scholar] [CrossRef] [PubMed]
- Herri, J.M.; Bouchemoua, A.; Kwaterski, M.; Fezoua, A.; Ouabbas, Y.; Cameirão, A. Gas hydrate equilibria for CO2–N2 and CO2–CH4 gas mixtures—Experimental studies and thermodynamic modelling. Fluid Phase Equilibria 2011, 301, 171–190. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds are not available from the authors. |







| a | b (MPa) | c | d (MPa) | e | f (MPa) | g | h |
|---|---|---|---|---|---|---|---|
| 1.00 | 0.55 | 1.00 | 1.02 | 1.00 | 1.90 | 1.00 | CS-I |
| 0.70 | 0.69 | 0.88 | 1.06 | 0.86 | 2.27 | 0.84 | CS-I |
| 0.50 | 0.83 | 0.76 | 1.26 | 0.73 | 2.62 | 0.70 | CS-I |
| 0.30 | 1.03 | 0.58 | 1.55 | 0.54 | 3.09 | 0.50 | CS-I |
| 0.00 | 1.66 | 0.00 | 2.40 | 0.00 | 4.20 | 0.00 | CS-I |
| a (MPa) | b (MPa) | c (MPa) | d (MPa) | e | f | g |
|---|---|---|---|---|---|---|
| 1.69 | 1.91 | 2.76 | 5.10 | 0.30 | 0.00 | CS-I |
| 2.08 | 2.45 | 3.37 | 6.44 | 0.21 | 0.09 | CS-I |
| 2.45 | 3.00 | 3.95 | 7.50 | 0.15 | 0.15 | CS-I |
| 2.98 | 3.87 | 4.74 | 9.00 | 0.09 | 0.21 | CS-I |
| 3.97 | 5.50 | 6.60 | 12.20 | 0.00 | 0.30 | CS-I |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belosludov, V.R.; Bozhko, Y.Y.; Subbotin, O.S.; Belosludov, R.V.; Zhdanov, R.K.; Gets, K.V.; Kawazoe, Y. Influence of N2 on Formation Conditions and Guest Distribution of Mixed CO2 + CH4 Gas Hydrates. Molecules 2018, 23, 3336. https://doi.org/10.3390/molecules23123336
Belosludov VR, Bozhko YY, Subbotin OS, Belosludov RV, Zhdanov RK, Gets KV, Kawazoe Y. Influence of N2 on Formation Conditions and Guest Distribution of Mixed CO2 + CH4 Gas Hydrates. Molecules. 2018; 23(12):3336. https://doi.org/10.3390/molecules23123336
Chicago/Turabian StyleBelosludov, Vladimir R., Yulia Yu. Bozhko, Oleg S. Subbotin, Rodion V. Belosludov, Ravil K. Zhdanov, Kirill V. Gets, and Yoshiyuki Kawazoe. 2018. "Influence of N2 on Formation Conditions and Guest Distribution of Mixed CO2 + CH4 Gas Hydrates" Molecules 23, no. 12: 3336. https://doi.org/10.3390/molecules23123336
APA StyleBelosludov, V. R., Bozhko, Y. Y., Subbotin, O. S., Belosludov, R. V., Zhdanov, R. K., Gets, K. V., & Kawazoe, Y. (2018). Influence of N2 on Formation Conditions and Guest Distribution of Mixed CO2 + CH4 Gas Hydrates. Molecules, 23(12), 3336. https://doi.org/10.3390/molecules23123336