Next Article in Journal
Gold and Nickel Extended Thiophenic-TTF Bisdithiolene Complexes
Next Article in Special Issue
Radical Polymerization of Alkyl 2-Cyanoacrylates
Previous Article in Journal
A Comparative Study of Human Saposins
Previous Article in Special Issue
Ultrafast Chemistry of Water Radical Cation, H2O•+, in Aqueous Solutions
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 23
Issue 2
10.3390/molecules23020423
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Microhydration and the Enhanced Acidity of Free Radicals

by
John C. Walton
EaStCHEM School of Chemistry, University of St. Andrews, St. Andrews KY16 9ST, UK
Molecules 2018, 23(2), 423; https://doi.org/10.3390/molecules23020423
Submission received: 31 January 2018 / Revised: 9 February 2018 / Accepted: 14 February 2018 / Published: 14 February 2018
(This article belongs to the Special Issue Radical Chemistry)
Browse Figures
Versions Notes

Abstract

:
Recent theoretical research employing a continuum solvent model predicted that radical centers would enhance the acidity (RED-shift) of certain proton-donor molecules. Microhydration studies employing a DFT method are reported here with the aim of establishing the effect of the solvent micro-structure on the acidity of radicals with and without RED-shifts. Microhydration cluster structures were obtained for carboxyl, carboxy-ethynyl, carboxy-methyl, and hydroperoxyl radicals. The numbers of water molecules needed to induce spontaneous ionization were determined. The hydration clusters formed primarily round the CO2 units of the carboxylate-containing radicals. Only 4 or 5 water molecules were needed to induce ionization of carboxyl and carboxy-ethynyl radicals, thus corroborating their large RED-shifts.

Graphical Abstract

1. Introduction

A transient-free radical is necessarily reactive at the site (X) of its unpaired electron (upe). In addition, a free radical with a structure containing a proton donor group may undergo ionic dissociation to a radical anion and a proton:
•XH2WAH→•XH2WA− + H+
in which W is a connector or spacer group, and A is the site of the departing proton. Effectively, the free radicals in this category can function as Brφnsted acids. More than 40 years ago, Hayon and Simic drew attention to the fact that free radicals could be more acidic than parent compounds [1]. Other pulse radiologists, particularly Steenken and co-workers, demonstrated analogous behavior for the radical cations of phenols and nucleosides [2,3]. Recently, several situations have been recognized in which the radical enhancement of proton dissociations has been of key importance. For example, Buckel, Zipse, and co-workers identified facile deprotonation of a β-keto-alkyl radical as the key step in an enzyme catalyzed dehydration of (R)-2-hydroxyglutaryl-CoA [4,5]. A similar key step was proposed in the analogous enzyme-catalyzed dehydration of (R)-2-hydroxy-4-methylpentanoyl-CoA [6]. Cyclohexadienyl type radicals are intermediates in numerous base-promoted homolytic aromatic substitution (BHAS) reactions; Studer and Curran have pinpointed their enhanced acidity as the driving force for these processes [7]. In addition, Radom and co-workers have published theoretical studies showing that, in general, CH2WOH radicals are more acidic than their parent CH3WOH alcohols [8,9].
A recent theoretical investigation of radicals containing carboxylic acid groups gave guidance as to what structural features are required for proton loss to be enhanced. The size of the effect and the identity of the connector groups that do and do not transmit the enhancement were also studied [10]. The term “RED-shift” was adopted as a short and convenient acronym for the phenomenon of Radical Enhancement of Dissociation. Appreciable RED-shifts were shown to occur for radicals dissociating to conjugate radical anions that allowed the displacement of an electronic charge away from their formal anionic centers coupled with displacement of spin density away from their formal radical centers.
A convenient measure of the RED-shift was found to be:
ΔpKa = pKa(model) − pKa(radical)
in which the models [HXH2WAH] were structurally identical to the radicals [•XH2WAH], except that the unpaired electrons had been replaced by -H-atoms.
The transient nature of most free radicals makes experimental determination of their pKa values difficult. Consequently, comparatively few radical acid dissociation constants have been measured, and error limits are necessarily high. Fortunately, computational methods for estimating pKas have been developed, and some of these refer directly to carboxylic acids [11,12,13,14,15,16]. These QM methods usually rely on computation of the free energies of deprotonation ΔGA-HA and, with this intent, a DFT functional suitable for C-centered free radicals was developed [17]. This method enabled several radicals that had large ΔpKa values to be pinpointed [10,18]. In this DFT method, the solvent (water) was allowed for simply by means of the CPCM continuum model [19]. A real possibility is that continuum solvent models would not be reliable for small and strong acids. Specific interactions of the solvent with the conjugate radical anions seem particularly likely because of their high charge densities. It is known that strong mineral acids spontaneously ionize in association with just a few microsolvating water molecules. For instance, both experiment and DFT computations showed that HCl dissociated into Cl−(H2O)3(H3O+) upon association with just four water molecules [20], and similar behavior was observed for other strong acids [21]. In fact, it has been noted that as the acidity of an acid increases, so the number of water molecules required to induce ionization (NGi) tends to decrease [17,22].
Theoretical studies of the microhydration of acids are challenging because the number of possible 3D arrays increases steeply as the number of water molecules increases. The potential energy surfaces (PES) rapidly become complex with many shallow minima. Distinguishing the global minimum from nearby local minima becomes problematic. Microhydration studies of transient acid radicals have been published for the bicarbonate radical 4H [17] and the hydroperoxyl radical 5H [23] (see Scheme 1). Some recent studies have shown that the limitations of the continuum models can be overcome with microhydration. For example, Close and Wardman studied di-hydration of the tyrosyl radical and discussed related structures [24]. The objectives of the present computational study were to investigate the effect microhydration has on the enhancement of acidity observed for specific free radicals with and without RED-shifts. Are the increased acidities computed with the continuum solvent model real? What effect does the upe in the radical have on the solvent microstructure? Can the number of water molecules needed to induce ionic dissociation (NGi) be determined for RED-shifted radicals?

2. Results and Discussion

A set of acid radicals with particular structural features was chosen for microhydration study and is shown in Scheme 1, together with experimental and computed pKa and ΔpKa values [10]. Three of the set contain carboxylic acid functional groups with differing spacer units. The carboxyl radicals 1Hc & 1Ht are very strong acids with large RED-shifts (ΔpKa = 3.9 & 3.2, respectively), and contain the upe formally right on the carboxylate C-atom. In carboxy-ethynyl radical anion 2, the upe and negative charge are formally separated by an ethynyl unit, which proved to be a very efficient conductor of RED-shift. In carboxy-methyl radical anion 3, the upe and negative charge are formally separated by a methylene unit that completely negated RED-shift. The set also contains the bicarbonate radical anion 4 that has the upe and carboxylic acid group formally separated by an O-atom. The final member, hydroperoxyl 5H, has a unique structure such that the upe and charge are formally on adjacent O-atoms. The ease of deprotonation of the acid radicals will be strongly influenced by solvation, which will stabilize the conjugate radical anions produced during dissociation more than the neutral radical precursors.
A benchmarking study involved comparison of 12 radical reaction types and 23 different DFT functionals (plus the MP2 ab-initio method), with the high level composite ab initio G4 method [25]. The CAM-B3LYP functional incorporating the Coulomb-attenuating method [26] gave lowest mean absolute deviations (MAD) and performed best with radical species [17]. Microhydration of the bicarbonate radical 4H, which has a large RED-shift, was investigated using this approach; cluster configurations were obtained for [HOC(O)O•·nH2O] with n = 1 to 8. That 4H was a very strong acid was confirmed by the finding that partial ionization spontaneously occurred with only 4 water molecules, and ionization was complete for 5 microsolvating water molecules, i.e., NGi = 5. The pKa of 4H obtained with this computational method (−1.2) was in satisfactory agreement with other estimates (see Scheme 1 and reference [17]). For each of the other radicals in Scheme 1 (•XH2WAH), optimized structures were obtained for hydrated clusters (•XH2WAH.nH2O) where n was increased until spontaneous dissociation (•XH2WA−.nH2O.H+) took place for some value of n (=NGi). Microhydrated cluster structures published by Maity and co-workers for structurally analogous formic [27] and trifluoroacetic acid [28] and by Leopold for various acids [21] served as useful models for the starting points for optimizations. The larger hydration clusters (n > ~8) displayed potential energy surfaces with quite a lot of shallow local minima, such that extensive searching was needed to find the global minima.

2.1. Microhydration of Carboxyl Radicals 1Hc and 1Ht

Carboxyl radicals are important in combustion processes and in the oxidation cycle of Earth’s atmosphere because of their formation from the reaction of CO with hydroxyl radicals. The pKa of 1H was determined to be −0.2 in a pioneering EPR spectroscopic study by Fessenden and co-workers [29]. The radical’s structures and reactions have also been studied experimentally by vibrational [30,31,32] and rotational spectroscopy [33,34,35], as well as by a number of high level QM computational methods [36,37]. Experiment and theory indicate that they exist as a pair of cis- and trans-conformers 1Hc and 1Ht separated by a torsional barrier of about 7.7 kcal/mol and with 1Ht about 1.7 kcal/mol lower in energy [35].
Microhydration of the cis-conformer [1Hc.nH2O] was examined for n = 1 to 8 and of the trans-conformer 1Ht for n = 1 to 12. The DFT method with the CAM-B3LYP functional and the 6-311+G(2d,p) basis set (see above) and including the CPCM solvent continuum model was employed. The PES for each value of n showed a series of minima and the global minimum energy cluster structures were obtained. Figure 1 shows the global minimum energy cluster structures for the cis-conformer associated with 1 to 6 H2O molecules.
For each value of n (except n = 1), a series of initial structures was tested. Two minima were found for 2 × H2O clusters, three minima were obtained for 3 × H2O clusters, and ten were obtained for the 4 × H2O clusters. In the latter case, several dissociated ion pairs were located as local minima [1.H+ 4H2O], and one of these was only 4.1 kcal/mol higher in energy than the global undissociated minimum shown in Figure 1. The minimum number of water molecules needed to obtain an ion pair as a local minimum was therefore NLi = 4. Ten minima were found for the 5 × H2O cluster and in this case the global minimum structure was an ion pair (Figure 1). Thus, the number of water molecules needed to render the hydrated ion pair [1. H+5H2O] a global minimum was NGi = 5. As expected, the number of possible local minima increased steadily with cluster size. For the structures of the global minimum clusters, the computed lengths of the radical acid A–H bonds (OC•O–H), rAH, and the lengths of the bonds from the leaving proton to the nearest H2O molecule, rHO, (see Figure 1) were useful indicators. These distances are plotted as a function of the number of H2O molecules in the global minimum clusters for radical 1Hc in Figure 2. The graph illustrates that rAH remained close to 1.0 Å in the 1× to 4 × H2O clusters and increased steeply to 1.47 Å in the ionized 5 × H2O cluster. This behavior was practically mirrored by the distances from the nearest water to the leaving proton (rHO), which remained in the 1.6 to 1.4 Å range for the 1 × to 4 × H2O clusters before steeply decreasing to 1.04 Å in the 5 × H2O cluster (see Figure 2).
Hydration of the trans-conformer 1Ht took a rather different course. As with 1Hc, a series of local minima was obtained for each hydration level. Cluster structures were more open, particularly for mono- to penta-hydration. A significantly higher level of hydration was required to induce ionization. Global energy minimum structures are illustrated in Figure 3 for selected clusters of 1Ht with 6 to 11 H2O molecules.
No clusters containing ionized 1Ht were obtained for 1× up to 9 × H2O components. For these clusters, the radical to proton bond length rAH remained steady at about 1.02 Å and the proton to water distance rHO also remained around 1.5 to 1.6 Å (see Figure 2). For 10 microsolvating H2O molecules, 9 minima were obtained including a local minimum only 2.3 kcal/mol above the global minimum, in which 1Ht was ionized (see Figure 3 for local and global minima). Finally, with 11 microsolvating H2O molecules, the global minimum structure contained the fully ionized radical [1.11H2O,H+] (Figure 3). Thus, for the trans-carboxyl radical NLi = 10 and NGi = 11.
At first, the much larger NGi for trans 1Ht than for cis 1Hc seemed surprising. In the case of 1Hc, the cis arrangement of the HO group with the adjacent C–O bond was a crucial feature. This enabled a first water molecule to H-bond to this OH and a second water molecule to simultaneously H-bond to the first water and to the carboxyl C–O, thus forming a 5-O-atom ring (see Figure 1, 1Hc.2H2O). Additional waters could then add whilst keeping ring structures intact. Finally, at NGi = 5, the structure evolved to an ionized 3D cage of rings in which the carboxyl moiety sensed two H-bonds and each water sensed at least two (1Hc.5H2O, Figure 1). This arrangement lowered the energy in relation to unionized clusters. With isomer 1Ht, however, the trans arrangement of the H–O group with the adjacent C–O precluded the possibility of two waters simultaneously H-bonding to the carboxyl and to each other. A larger, more open ring of waters was needed to stretch from one side of the carboxyl group to the other (see 1Ht.7H2O, Figure 3). In fact, the weaker H-bonds that resulted meant that four water H-bonds to the carboxyl were required before ionization could take place (see 1Ht.11H2O, Figure 3).
As mentioned above, 1Ht is lower in energy than 1Hc in the gas phase. For the solvated clusters, the difference in DFT computed energies between 1Hc and 1Ht [ΔE(c–t)/kcal/mol] are plotted against the number of cage water molecules in Figure 4.
It is evident that the trans-clusters are lower in energy for 0 to 2 cluster H2O, but that the cis-clusters are lower in energy for 3 to 7 microsolvating H2O molecules. In aqueous solution, therefore, thermodynamic control should ensure complete deprotonation by five waters. Hence, the experimental pKa of −0.2 [29] probably corresponds to 1Hc.

2.2. Microhydration of Carboxy-ethynyl 2H and Carboxy-methyl 3H Radicals

The formal structure of the carboxy-ethynyl radical anion 2 (Scheme 1) suggests the upe and charge are separated by the ethyne unit. However, DFT computations predicted 2H to be a much stronger acid than propiolic acid (HC≡CCO2H, pKa = 1.74) and hence to have a sizeable RED-shift [10]. Furthermore, much site exchange of spin and charge was computed for 2 with significant negative charge associated with the terminal ethyne C-atom. This was revealed by the Mulliken electronic charges (Figure 5), with the red numbers denoting negative charge. It followed that the normally hydrophobic C≡C unit might, in radical 2H, take part in H-bonding to H2O, although the electrostatic potential surface (ESP, Figure 5) was fairly featureless, except for the negatively charged (red) O-atoms. It was of special interest therefore to examine microhydration of 2H to check the prospect of the H2O clusters extending around to the C≡C terminus, as well as to confirm the enhanced acidity of this species. In the lowest energy structures for clusters with 3 and 4 H2O molecules (see Figure 5), H-bonding took place exclusively in the carboxyl unit. Addition of four H2O molecules caused spontaneous ionization, and the ionized structure was the global minimum. No ionized minima were found for clusters with only three H2O molecules and hence NLi = NGi = 4. This was confirmed by the sudden increase in rAH and decrease in rHO for greater than 4 × H2O shown on Figure 2. The small NLi and NGi agree well with the high predicted acidity (negative pKa) for 2H.
The global minimum structure on addition of 5 H2O molecules was the ionized cage structure shown in Figure 5. However, a unionized structure (Figure 5), obtained simply by expansion of the outer ring of the 2H.4H2O cluster, was only 2.6 kcal/mol higher in energy. Another local minimum of the 2H.5H2O system did exhibit H-bonding to the terminal atom of the ethyne unit as part of a ring connected to a carboxyl O-atom (Figure 5). However, this cluster was 10 kcal/mol higher in energy than the global minimum [38]. We deduce that H-bonding of H2O molecules to the ethyne unit of 2H did not stabilize the conjugate radical anion 2.
Although the charge and upe in the carboxy-methyl radical 3H are formally separated by only the one C-atom of the methylene group, this radical was a much weaker acid than 2H and comparable in strength to acetic acid. Unlike the ethyne unit, the CH2 spacer did not transmit any RED-shift to the carboxyl group. The computational results indicated negative electronic charges associated only with the carboxyl O-atoms and, in agreement, the ESP surface also showed no negative features adjoining the CH2 group (see Figure 6). In the cluster for 3H with only a few H2O molecules, they H-bonded with the carboxyl group and the structures resembled the analogous clusters for 2H, except that ionization was not observed. Compare, for example, 2H.4H2O (ionized) of Figure 5 with 3H.4H2O (undissociated) of Figure 6. In striking agreement with the lesser acidity and zero RED-shift of 3H, ionized structures only appeared as local minima for 3H.6H2O (3.6 kcal/mol above the global minimum) and 3H.7H2O (1.6 kcal/mol above the global minimum), finally becoming the global minimum for 3H.8H2O (see Figure 6). Figure 2 shows the abrupt increase in rAH and abrupt decrease in rHO above 7 × H2O, and hence it follows that NLi = 6 and NGi = 8. Investigations showed large numbers of local minima, differing in energy by < ~6 kcal/mol, for the 3H.9H2O, 3H.10H2O, 3H.11H2O, and 3H.12H2O clusters, with some ionized and some undissociated. No clusters involving H-bonding to the CH2 group were found, even with these larger water shells. The elegant optimum structure found for the 3H.12H2O cluster (Figure 6) consisted of a symmetrical cage of 5-member O-atom rings, atop a planar 3H.2H2O unit, forming part of a quasi-dodecahedron. The PES could only be partially explored for 3H.12H2O, so it is not known if this is a local or global minimum.

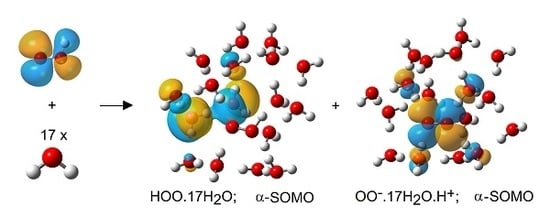
2.3. Microhydration of Hydroperoxyl Radicals 5H

The hydroperoxyl radical/superoxide radical anion conjugate pair (5H/5) has been intensively studied over many years. It plays important roles in lipid peroxidations and in atmospheric chemistry [39,40,41,42,43,44]. The hydroperoxyl radical differs from the other acid radicals of this study in that it contains two adjacent O-atoms rather than the carboxyl unit. It was anticipated, therefore, that the hydrated clusters would have significantly different features. Microhydration of the hydroperoxyl radical 5H was previously investigated by Novoa and co-workers for n = 1–4 and n = 10 using the HF/6-31++G(d,p) level of theory [23]. The adsorption and acid dissociation process of 5H on the surface of (H2O)20 and (H2O)21 clusters were also studied computationally [45]. Not unexpectedly, the CAM-B3LYP/6-311+G(2d,p) method employed here, except for n = 1 and 2, gave somewhat different minimum energy structures for hydrated clusters.
The minimum energy cluster structures of 5H.nH2O were all un-ionized forms for n = 1 to 11; selected examples are in Figure 7 [the rAH and rHO lengths are in Figure 2]. The 5H.2H2O structure was similar in essence to analogous carboxy 2×H2O clusters (above). A noteworthy feature for the 4xH2O clusters was that structure 5H.4H2O(a) containing a 6-O-atom ring but only 5 H-bonds was lower in energy by 5.4 kcal/mol than structure (c) containing 6 H-bonds (Figure 7). The three H-bonds from waters to the OO unit in structure 5H.4H2O(c) are all very long (1.874, 2.079, and 2.431 Å), probably because of angle strain in the two small 4-O-rings. In contrast, the H-bond from water to the OO unit in structure 5H.4H2O(a) is shorter (1.853 Å) and the inter-water H-bonds (1.653, 1.712, and 1.737 Å) are considerably shorter than those of 5H.4H2O(c). Structure 5H.4H2O(b), which contains a 5-O-ring, is intermediate in energy, and the inter-water H-bonds (1.682, 1.786, 1.857 Å) are also intermediate in length.
3D cage structures were composed of rings of waters predominated for clusters with 7 or more waters and increased in complexity as more waters were added (see Figure 7). The 3D structures of the 5H.14H2O and 5H.16H2O clusters contained four H-bonds to the OO unit, and the number of inter-water H-bonds tended to a maximum.
The first cage containing ionized O2−• and H+ appeared for n = 12, but was 4.3 kcal/mol higher in energy than the undissociated minimum energy structure. It was not possible to exhaustively explore the entire potential energy landscapes for n = 12, 13, 14, 15, and 16. For each of these clusters, both ionized and un-ionized forms were obtained, which differed in energy by < ~10 kcal/mol but with un-ionized cages as energy minima. For the 5H.17H2O cluster, 11 local minima were obtained, with 9 being ionized and 2 un-ionized. The lowest energy ionized and un-ionized structures are illustrated in Figure 8. A remarkable result was the smallness of the structural difference that brought about spontaneous dissociation. The relocation of the single water molecule (labelled “a” in Figure 8) from one peripheral site to another was sufficient. This ostensibly minor change, together with concomitant bond length and angle reorganizations, caused a 5 kcal/mol lowering of the energy! NLi and NGi were estimated to be 13 and 17, respectively (see Figure 2). However, these larger hydration clusters probably existed as equilibria to which both ionized and un-ionized cages contributed. Under these circumstances, the “number of water molecules needed to induce ionization” (NGi) is probably a fuzzy concept and should probably not be considered as a sharply defined integer. In support of this, note the less abrupt change in the rAH and rHO distances for larger values of n in the 5H.nH2O clusters as shown in Figure 2.

2.4. Microhydration, Acidity, and RED-Shift

The computed numbers of water molecules needed to induce ionization in the radicals NGi are compared with literature data for mineral acids in Figure 9. Qualitatively, the data make good sense. Radicals 1Hc, 2H, and 4H required only 4 or 5 water molecules to induce deprotonation, i.e., a similar number to acids such as HNO3 and CF3COOH. This agrees well with the previous computation of their pKa values in the same range as mineral acids and gives an independent confirmation of the reality of their RED-shifts.
The trans-carboxyl radical 1Ht was an obvious outlier and, as explained above, its greater NGi stems from the somewhat artificial trans-structure that, in a real solution, will convert to cis. The carboxy-methyl radical 3H resembled a ‘normal’ carboxylic acid and needed the same number of water molecules to induce dissociation as formic (and probably acetic) acid. Thus, the microhydration study confirmed the lack of RED-shift for this radical. The data point for the HOO• (5H) lies far away from those of the mineral and carboxylate-containing radicals. The radical character of 5H greatly increases its acidity compared to that of H2O2. Structurally, however, the negative charge distributed to two adjacent O-atoms of superoxide is much more compact than on the two O-atoms of carboxylates. A large cage of water molecules was needed to stabilize this compact conjugate radical anion. That it diverges from the other acid radicals is not at all surprising.

3. Materials and Methods

DFT calculations were carried out using the Gaussian 09 suite of programs [46]. The CAM-B3LYP functional [26] with the 6-311+G(2d,p) basis set was employed for most species with the CPCM continuum model [19] with water as solvent. This model is derived from the COSMO model. Default values of the keywords Alpha, Radii, TSNUM, and TSARE were employed. Based on previous work with free radicals, the CAM-B3LYP functional, which combines the hybrid qualities of B3LYP with the long-range correction proposed by Tawada et al. [47], gave the best results in comparison with G4 (MAD: 2.5 kcal/mol. Functionals of comparable accuracy, such as BMK (MAD 3.2 kcal mol−1), ωB97 (MAD 3.3 kcal mol−1), and M05 (MAD 3.6 kcal mol−1), displayed no significant computational time advantages. Vibrational frequency calculations were implemented so that GS (no imaginary frequencies) and TS status could be checked (one imaginary frequency), and enthalpies and free energies were adjusted for zero point and thermal corrections to 1 atm and 298 K.

4. Conclusions

From this study of the structures of hydrated acid radicals, the following factors that reduced the energy of the hydrated species were identified: (i) H-bonding of water to the acidic proton of the radical; (ii) as many H-bonds from waters to the O-atoms of the radical as possible; (iii) as many H-bonds as possible (usually 2 or more) for each water molecule; (iv) rings of O-atoms (particularly 5- and 6-membered) were favored over chains or dangling waters for the larger hydrated clusters. The hydration clusters formed primarily round the CO2 units of the carboxylate-containing radicals and not round either of the CH2 or C≡C moieties that protruded from the cages. This held true even though the DFT study indicated considerable negative charge associated with the C≡C unit of the carboxy-ethynyl radical 2H.
Although trans-carboxyl (1Ht) was lower in energy than 1Hc in the gas phase, on microhydration the cis-clusters became lower in energy after only 3 solvating H2O molecules. In general, therefore, any carboxylic acid RCO2H in aqueous solution will probably convert to its cis-conformation and ionize from that.
It had previously been predicted that radicals 1Hc, 2H, and 4H would be very strong acids with large RED-shifts [10,18]. The present finding, that just a few water molecules (4 to 5) were sufficient to induce spontaneous ionization of each one, was a valuable, independent corroboration of this. Interestingly, the RED-shift of the carboxy-ethynyl radical 2H was found not to be due to solvation of its C≡C section. The increased stability of its conjugate radical anion 2 was due to other causes; probably stronger H-bonding to the carboxylate. Additionally, essentially zero RED-shift had been predicted for the carboxy-methyl radical 3H, despite its rather similar structure. The microhydration study was again in full agreement and indicated that many more water molecules (8) were needed to induce ionization of 3H.

Acknowledgments

The author thanks EaStCHEM for financial support.

Conflicts of Interest

The author declares no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References and Notes

  1. Hayon, E.; Simic, M. Acid-base Properties of Free Radicals in Solution. Acc. Chem. Res. 1974, 7, 114–121. [Google Scholar] [CrossRef]
  2. Steenken, S.; Telo, J.P.; Novais, H.M.; Candeias, L.P. One-electron-reduction Potentials of Pyrimidine Bases, Nucleosides, and Nucleotides in Aqueous Solution. Consequences for DNA redox Chemistry. J. Am. Chem. Soc. 1992, 114, 4701–4709. [Google Scholar] [CrossRef]
  3. Steenken, S.; Neta, P. One-electron Redox Potentials of Phenols. Hydroxy- and Aminophenols and Related Compounds of Biological Interest. J. Phys. Chem. 1982, 86, 3661–3667. [Google Scholar] [CrossRef]
  4. Buckel, W.; Keese, R. One-electron Redox Reactions of CoASH Esters in Anaerobic Bacteria—A Mechanistic Proposal. Angew. Chem. Int. Ed. 1995, 34, 1502–1506. [Google Scholar] [CrossRef]
  5. Smith, D.M.; Buckel, W.; Zipse, H. Deprotonation of Enoxy Radicals: Theoretical Validation of a 50-Year-Old Mechanistic Proposal. Angew. Chem. Int. Ed. 2003, 42, 1867–1870. [Google Scholar] [CrossRef] [PubMed]
  6. Kim, J.; Darley, D.J.; Buckel, W.; Pierik, A.J. An Allylic Ketyl Radical Intermediate in Clostridial Amino-acid Fermentation. Nat. Chem. 2008, 44, 239–242. [Google Scholar] [CrossRef] [PubMed]
  7. Studer, A.; Curran, D.P. The Electron is a Catalyst. Nat. Chem. 2014, 50, 765–773. [Google Scholar] [CrossRef] [PubMed]
  8. Mayer, P.M.; Radom, L. Deprotonating Molecules and Free Radicals to Form Carbon-Centered Anions: A G2 ab Initio Study of Molecular and Free Radical Acidity. J. Phys. Chem. A 1998, 102, 4918–4924. [Google Scholar] [CrossRef]
  9. Morris, M.; Chan, B.; Radom, L. Effect of Protonation State and Interposed Connector Groups on Bond Dissociation Enthalpies of Alcohols and Related Systems. J. Phys. Chem. A 2014, 118, 2810–2819. [Google Scholar] [CrossRef] [PubMed]
  10. Walton, J.C. Radical-Enhanced Acidity: Why Bicarbonate, Carboxyl, Hydroperoxyl, and Related Radicals Are So Acidic. J. Phys. Chem. A 2017, 121, 7761–7767. [Google Scholar] [CrossRef] [PubMed]
  11. Schmidt am Busch, M.; Knapp, E.-W. Accurate pKa Determination for a Heterogeneous Group of Organic Molecules. ChemPhysChem 2004, 5, 1513–1522. [Google Scholar] [CrossRef] [PubMed]
  12. Silva, C.O.; da Silva, E.C.; Nascimento, M.A.C. Ab initio Calculations of Absolute pKa Values in Aqueous Solution. Part 2. Aliphatic Alcohols, Thiols, and Halogenated Carboxylic Acids. J. Phys. Chem. A 2000, 104, 2402–2409. [Google Scholar] [CrossRef]
  13. Klicic, J.J.; Freisner, R.A.; Liu, S.-Y.; Guida, W.C. Accurate Prediction of Acidity Constants in Aqueous Solution via Density Functional Theory and Self-Consistent Reaction Field Methods. J. Phys. Chem. A 2002, 106, 1327–1335. [Google Scholar] [CrossRef]
  14. Klamt, A.; Eckert, F.; Diedenhofen, M.; Beck, M.E. First Principles Calculations of Aqueous pKa Values for Organic and Inorganic Acids Using COSMO-RS Reveal an Inconsistency in the Slope of the pKa Scale. J. Phys. Chem. A 2003, 107, 9380–9386. [Google Scholar] [CrossRef] [PubMed]
  15. Zhang, S.; Baker, J.; Pulay, P.A. Reliable and Efficient First Principles-Based Method for Predicting pKa Values. 1. Methodology. J. Phys. Chem. A 2010, 114, 425–431. [Google Scholar] [CrossRef] [PubMed]
  16. Zhang, S.; Baker, J.; Pulay, P.A. Reliable and Efficient First Principles-Based Method for Predicting pKa Values. 2. Organic Acids. J. Phys. Chem. A 2010, 114, 432–442. [Google Scholar] [CrossRef] [PubMed]
  17. Bühl, M.; DaBell, P.; Manley, D.W.; McCaughan, R.P.; Walton, J.C. Bicarbonate and Alkyl Carbonate Radicals: Structural Integrity and Reactions with Lipid Components. J. Am. Chem. Soc. 2015, 137, 16153–16162. [Google Scholar] [CrossRef] [PubMed]
  18. Walton, J.C. Enhanced Proton Loss from Neutral Free Radicals: Towards Carbon-Centered Superacids. J. Phys. Chem. A 2018, 122. [Google Scholar] [CrossRef] [PubMed]
  19. Barone, V.; Cossi, M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
  20. Gutberlet, A.; Schwaab, G.; Birer, O.; Masia, M.; Kaczmarek, A.; Forbert, H.; Havenith, M.; Marx, D. Science 2009, 324, 1545–2212. [CrossRef] [PubMed]
  21. Leopold, K.R. Hydrated Acid Clusters. Annu. Rev. Phys. Chem. 2011, 62, 327–349. [Google Scholar] [CrossRef] [PubMed]
  22. Weber, K.H.; Tao, F.M. Ionic Dissociation of Perchloric Acid in Microsolvated Clusters. J. Phys. Chem. A 2001, 105, 1208–1213. [Google Scholar] [CrossRef]
  23. Del Valle, C.P.; Valdemoro, C.; Novoa, J.J. The Determinant Role of Water in the Ionic Dissociation of HO2. J. Mol. Struct. THEOCHEM 1996, 371, 143–152. [Google Scholar] [CrossRef]
  24. Close, D.M.; Wardman, P. Calculation of Standard Reduction Potentials of Amino Acid Radicals and the Effects of Water and Incorporation into Peptides. J. Phys. Chem. A 2018, 122, 439–445. [Google Scholar] [CrossRef] [PubMed]
  25. Curtiss, L.A.; Redfern, P.C.; Raghavachari, K. Gaussian-4 Theory. J. Chem. Phys. 2007, 126, 84108–84119. [Google Scholar] [CrossRef] [PubMed]
  26. Yanai, T.; Tew, D.P.; Handy, N.C. A New Hybrid Exchange-correlation Functional Using the Coulomb-attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
  27. Maity, D.K. How Much Water Is Needed To Ionize Formic Acid? J. Phys. Chem. A 2013, 117, 8660–8670. [Google Scholar] [CrossRef] [PubMed]
  28. Krishnakumar, P.; Maity, D.K. Effect of microhydration on dissociation of trifluoroacetic acid. J. Phys. Chem. A 2014, 118, 5443–5453. [Google Scholar] [CrossRef] [PubMed]
  29. Jeevarajan, A.S.; Carmichael, I.; Fessenden, R.W. ESR Measurement of the pKa of Carboxyl Radical and ab initio Calculation of the Carbon-13 Hyperfine Constant. J. Phys. Chem. 1990, 94, 1372–1376. [Google Scholar] [CrossRef]
  30. Forney, D.; Jacox, M.E.; Thompson, W.E. Infrared Spectra of trans-HOCO, HCOOH+, and HCO2− Trapped in Solid Neon. J. Chem. Phys. 2003, 119, 10814–10823. [Google Scholar] [CrossRef]
  31. Johnson, C.J.; Otto, R.; Continetti, R.E. Spectroscopy and Dynamics of the HOCO Radical: Insights into the OH + CO → H + CO2 Reaction. Phys. Chem. Chem. Phys. 2014, 16, 19091–19105. [Google Scholar] [CrossRef] [PubMed]
  32. Ryazantsev, S.V.; Feldman, V.I.; Khriachtchev, L. Conformational Switching of HOCO Radical: Selective Vibrational Excitation and Hydrogen-Atom Tunneling. J. Am. Chem. Soc. 2017, 139, 9551–9557. [Google Scholar] [CrossRef] [PubMed]
  33. Radford, H.E.; Wei, W. The rotational spectrum of trans-HOCO and DOCO. J. Chem. Phys. 1992, 97, 3989–3995. [Google Scholar] [CrossRef]
  34. Oyama, T.; Funato, W.; Sumiyoshi, Y.; Endoa, Y. Observation of the Pure Rotational Spectra of trans- and cis-HOCO. J. Chem. Phys. 2011, 134, 174303–174307. [Google Scholar] [CrossRef] [PubMed]
  35. McCarthy, M.C.; Martinez, O.; McGuire, B.A.; Crabtree, K.N.; Martin-Drumel, M.-A.; Stanton, J.F. Isotopic Studies of trans- and cis-HOCO Using Rotational Spectroscopy: Formation, Chemical Bonding, and Molecular Structures. J. Chem. Phys. 2016, 144, 124304. [Google Scholar] [CrossRef] [PubMed]
  36. Li, Y.; Francisco, J.S. High Level ab initio Studies on the Excited States of HOCO Radical. J. Chem. Phys. 2000, 113, 7963–7970. [Google Scholar] [CrossRef]
  37. Conte, R.; Houston, P.L.; Bowman, J.M. Communication: A Benchmark-quality, Full-dimensional ab initio Potential Energy Surface for Ar-HOCO. J. Chem. Phys. 2014, 140, 151101. [Google Scholar] [CrossRef]
  38. As a cross check suggested by a reviewer, structures of the 4×H2O and 5×H2O clusters of 2H were optimized with the CAM-B3LYP-D3/6-311+G(2d,p) method to include Grimme’s empirical dispersion corrections. The SMD solvent continuum model was also employed. For each a range of different starting geometries was tried. For both cluster types this method arrived at the same global minimum structures 2H.4H2O and 2H.5H2O shown in Figure 5. There were some differences in bond lengths and angles. Furthermore, the cluster of the 2H.5H2O system exhibiting H-bonding to the terminal atom of the ethyne unit as part of a ring connected to a carboxyl O-atom (Figure 5) was again found to be only a local minimum but 7 kcal/mol higher in energy.
  39. Bielski, B.H.J.; Cabelli, D.E.; Arudi, R.L.; Ross, A.B. Reactivity of HO2/O2− Radicals in Aqueous Solution. J. Phys. Chem. Ref. Data 1985, 14, 1041–1100. [Google Scholar] [CrossRef]
  40. Mendes, J.; Zhou, C.-W.; Curran, H.J. Theoretical Chemical Kinetic Study of the H-Atom Abstraction Reactions from Aldehydes and Acids by H Atoms and OH, HO2, and CH3 Radicals. J. Phys. Chem. A 2014, 118, 12089–12104. [Google Scholar] [CrossRef] [PubMed]
  41. Farnia, S.; Vahedpour, M.; Abedi, M.; Farrokhpour, H. Theoretical Study on the Mechanism and Kinetics of Acetaldehyde and Hydroperoxyl Radical: An Important Atmospheric Reaction. Chem. Phys. Lett. 2013, 583, 190–197. [Google Scholar] [CrossRef]
  42. Iuga, C.; Alvarez-Idaboy, J.R.; Russo, N. Antioxidant Activity of trans-Resveratrol toward Hydroxyl and Hydroperoxyl Radicals: A Quantum Chemical and Computational Kinetics Study. J. Org. Chem. 2012, 77, 3868–3877. [Google Scholar] [CrossRef] [PubMed]
  43. Espinosa-Garcia, J. Theoretical Study of the Trapping of the OOH Radical by Coenzyme Q. J. Am. Chem. Soc. 2004, 126, 920–927. [Google Scholar] [CrossRef] [PubMed]
  44. Yin, H.; Xu, L.; Porter, N.A. Free Radical Lipid Peroxidation: Mechanisms and Analysis. Chem. Rev. 2011, 111, 5944–5972. [Google Scholar] [CrossRef] [PubMed]
  45. Torrent-Sucarrat, M.; Ruiz-Lopez, M.F.; Martins-Costa, M.; Francisco, J.S.; Anglada, J.M. Protonation of Water Clusters Induced by Hydroperoxyl Radical Surface Adsorption. Chem. Eur. J. 2011, 17, 5076–5085. [Google Scholar] [CrossRef] [PubMed]
  46. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
  47. Tawada, Y.; Tsuneda, T.; Yunagisawa, S.; Yanai, T.; Hirao, K. A Long-Range-Corrected Time-Dependent Density Functional Theory. J. Chem. Phys. 2004, 120, 8425–8433. [Google Scholar] [CrossRef] [PubMed]
Structure Availability: Cartesian matrices of the optimum clusters are available from the author.
Molecules 23 00423 sch001 550
Scheme 1. Set of Acid Radicals for Microhydration Study. Experimental pKa values with DFT computed values in parenthesis.
Scheme 1. Set of Acid Radicals for Microhydration Study. Experimental pKa values with DFT computed values in parenthesis.
Molecules 23 00423 sch001
Molecules 23 00423 g001 550
Figure 1. Optimized Cluster Structures of cis-Carboxyl (1Hc) with 1 to 6 H2O molecules.
Figure 1. Optimized Cluster Structures of cis-Carboxyl (1Hc) with 1 to 6 H2O molecules.
Molecules 23 00423 g001
Molecules 23 00423 g002 550
Figure 2. Microhydrated acid radicals (DFT optimized structures): plots of computed distances rAH, and to the nearest water rHO, versus the number of solvating waters (n). Data for 4H (HOCOO, black), 1Ht (t-HOCO, blue), 1Hc (c-HOCO, red), 3H (H2CCOOH, yellow), 2H (CCCOOH, purple), and 5H (HOO, green).
Figure 2. Microhydrated acid radicals (DFT optimized structures): plots of computed distances rAH, and to the nearest water rHO, versus the number of solvating waters (n). Data for 4H (HOCOO, black), 1Ht (t-HOCO, blue), 1Hc (c-HOCO, red), 3H (H2CCOOH, yellow), 2H (CCCOOH, purple), and 5H (HOO, green).
Molecules 23 00423 g002
Molecules 23 00423 g003 550
Figure 3. Optimized Cluster Structures of trans-Carboxyl (1Ht) with 6 to 11 H2O molecules. Departing proton shown in green.
Figure 3. Optimized Cluster Structures of trans-Carboxyl (1Ht) with 6 to 11 H2O molecules. Departing proton shown in green.
Molecules 23 00423 g003
Molecules 23 00423 g004 550
Figure 4. Graph of the Difference in the Energies (kcal/mol) of the 1Hc and 1Ht hydrated clusters as a function of the number of cluster water molecules.
Figure 4. Graph of the Difference in the Energies (kcal/mol) of the 1Hc and 1Ht hydrated clusters as a function of the number of cluster water molecules.
Molecules 23 00423 g004
Molecules 23 00423 g005 550
Figure 5. Optimized Structures of Hydration Clusters for Carboxy-ethynyl Radical 2H and Radical Anion 2. Mulliken charge: negative in red, positive in blue.
Figure 5. Optimized Structures of Hydration Clusters for Carboxy-ethynyl Radical 2H and Radical Anion 2. Mulliken charge: negative in red, positive in blue.
Molecules 23 00423 g005
Molecules 23 00423 g006 550
Figure 6. Optimized Structures of Hydration Clusters for Carboxy-methyl Radical 3H and Radical Anion 3. Mulliken charges: negative in red, positive in blue.
Figure 6. Optimized Structures of Hydration Clusters for Carboxy-methyl Radical 3H and Radical Anion 3. Mulliken charges: negative in red, positive in blue.
Molecules 23 00423 g006
Molecules 23 00423 g007 550
Figure 7. Optimum Structures of Selected HOO• Radical/Water Clusters (5H.nH2O).
Figure 7. Optimum Structures of Selected HOO• Radical/Water Clusters (5H.nH2O).
Molecules 23 00423 g007
Molecules 23 00423 g008 550
Figure 8. Ionized (left) and un-ionized (right) clusters of the hydroperoxyl radical (5H) with 17 H2O molecules. [Bond to departing H+ highlighted in green.].
Figure 8. Ionized (left) and un-ionized (right) clusters of the hydroperoxyl radical (5H) with 17 H2O molecules. [Bond to departing H+ highlighted in green.].
Molecules 23 00423 g008
Molecules 23 00423 g009 550
Figure 9. Plots of pKa versus the number of microsolvating water molecules needed to cause ionization.
Figure 9. Plots of pKa versus the number of microsolvating water molecules needed to cause ionization.
Molecules 23 00423 g009

Share and Cite

MDPI and ACS Style

Walton, J.C. Microhydration and the Enhanced Acidity of Free Radicals. Molecules 2018, 23, 423. https://doi.org/10.3390/molecules23020423

AMA Style

Walton JC. Microhydration and the Enhanced Acidity of Free Radicals. Molecules. 2018; 23(2):423. https://doi.org/10.3390/molecules23020423

Chicago/Turabian Style

Walton, John C. 2018. "Microhydration and the Enhanced Acidity of Free Radicals" Molecules 23, no. 2: 423. https://doi.org/10.3390/molecules23020423

APA Style

Walton, J. C. (2018). Microhydration and the Enhanced Acidity of Free Radicals. Molecules, 23(2), 423. https://doi.org/10.3390/molecules23020423

Article Metrics

Back to TopTop