Next Article in Journal
Pioneer Factors in Animals and Plants—Colonizing Chromatin for Gene Regulation
Next Article in Special Issue
Theoretical Study of the C2H5 + HO2 Reaction: Mechanism and Kinetics
Previous Article in Journal
Physicochemical Characterization, Antioxidant and Immunostimulatory Activities of Sulfated Polysaccharides Extracted from Ascophyllum nodosum
Previous Article in Special Issue
Theoretical Studies on Catalysis Mechanisms of Serum Paraoxonase 1 and Phosphotriesterase Diisopropyl Fluorophosphatase Suggest the Alteration of Substrate Preference from Paraoxonase to DFP
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 23
Issue 8
10.3390/molecules23081913
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Molecular Electron Density Theory Study of the Competitiveness of Polar Diels–Alder and Polar Alder-ene Reactions

by
Luis R. Domingo
1,*,
Mar Ríos-Gutiérrez
1 and
Patricia Pérez
2
1
Department of Organic Chemistry, University of Valencia, Moliner 50, 46100 Valencia, Spain
2
Facultad de Ciencias Exactas, Departamento de Ciencias Químicas, Universidad Andres Bello, Av. República 498, Santiago 8370146, Chile
*
Author to whom correspondence should be addressed.
Molecules 2018, 23(8), 1913; https://doi.org/10.3390/molecules23081913
Submission received: 16 July 2018 / Revised: 27 July 2018 / Accepted: 28 July 2018 / Published: 31 July 2018
(This article belongs to the Special Issue Theoretical Investigations of Reaction Mechanisms)
Browse Figures
Versions Notes

Abstract

:
The competitiveness of the BF3 Lewis acid (LA) catalyzed polar Diels–Alder (P-DA) and polar Alder-ene (P-AE) reactions of 2-methyl-1,3-butadiene, a diene possessing an allylic hydrogen, with formaldehyde has been studied within the Molecular Electron Density Theory (MEDT) at the MPWB1K/6-311G(d,p) computational level. Coordination of BF3 LA to the oxygen of formaldehyde drastically accelerates both reactions given the high electrophilic character of the BF3:formaldehyde complex. As a consequence, these reactions present a very low activation enthalpy—less than 2.2 kcal·mol−1—thus becoming competitive. In dioxane, the P-AE reaction is slightly favored because of the larger polar character of the corresponding transition state structure (TS). In addition, the Prins reaction between hexahydrophenanthrene and the BF3:formaldehyde complex has also been studied as a computational model of an experimental P-AE reaction. For this LA-catalyzed reaction, the P-DA reaction presents very high activation energy because of the aromatic character of the dienic framework. The present MEDT study allows establishing the similarity of the TSs associated with the formation of the C–C single bond in both reactions, as well as the competitiveness between P-AE and P-DA reactions when the diene substrate possesses at least one allylic hydrogen, thus making it necessary to be considered by experimentalists in highly polar processes. In this work, the term “pseudocyclic selectivity” is suggested to connote the selective formation of structural isomers through stereoisomeric pseudocyclic TSs.

Graphical Abstract

1. Introduction

The Diels–Alder (DA) reaction between a conjugated diene and an ethylene yielding a cyclohexene derivative, reported for the first time by Otto Diels and Kurt Alder in 1927 [1], is one of the most studied organic reactions from a synthetic as well as theoretical point of view (see Scheme 1) [2,3].
On the other hand, the Alder-ene (AE) reaction, first reported by Kurt Alder in 1943 [4], which involves an alkene with an allylic C–H bond and an ethylene derivative, is one of the simplest ways to achieve the formation of a C–C single bond (see Scheme 2) [5].
Mechanistically, both DA and AE reactions were classified as pericyclic reactions [7,8], in which “all first order changes in bonding relationships take place in concert on a closed curve” [9]. However, a recent MEDT [10] study of the unfavorable DA and AE reactions of 1,3-butadiene 6 and propene 4 with ethylene 7 showed that the bonding changes in these reactions take place sequentially, and not in a simultaneous (concerted) cyclic rearrangement, thus ruling out the pericyclic mechanism [11]. That MEDT study emphasized that the high activation energies associated to these pseudocyclic reactions are due to the high-energy costs demanded for the rupture of the C–C double bonds present in the unsaturated hydrocarbon reagents.
A density functional theory [12] (DFT) study of the DA reactions between cyclopentadiene (Cp) 1 and a series of ethylenes 8 of increased electrophilic character, easily taking place experimentally, allowed establishing the polar mechanism in which the feasibility of DA reactions depends on their polar character; i.e., the increase of the nucleophilic character of the diene as well as the electrophilic character of the ethylene, or vice versa, making the reaction easier (see Scheme 3) [13]. Along this series of polar DA (P-DA) reactions, the increase of the polar character of the reaction, measured by the global electron density transfer [14] (GEDT) at the corresponding transition state structures (TSs), decreases the activation energies [15].
The mechanism of the AE reactions between isobutene 10 and twelve ethylenes of increased electrophilicity was recently studied (see Scheme 4) [16]. Just as in P-DA reactions [13], a very good correlation between the activation energies and the GEDT computed at the corresponding TSs was found [16]; i.e., the more polar the AE reaction, the faster it is.
The molecular mechanisms of the P-DA [13] and polar AE (P-AE) [16] reactions present a great similarity—both are initialized by the nucleophilic attack of the terminal carbon of the butadiene or the propene on the most electrophilic center of the ethylene derivative. The subsequent ring closure, in the case of the P-DA reaction, or hydrogen abstraction, in the case of the P-AE reaction, take place after passing the corresponding TS in a straightforward manner towards the final product of the reactions. Consequently, in molecules such as 2-methyl-1,3-butadiene (2MBD) 14, which possesses a 1,3-butadiene framework and at least one allylic hydrogen, both P-DA and P-AE reactions can be competitive pathways (see Scheme 5).
In this sense, in 1991 Künzer et al. studied the dimethylchloride aluminium LA-mediated Prins reaction [17] of steroidal olefin 17 with paraformaldehyde yielding homoallylic alcohols 18 and 19 (see Scheme 6) [18]. The DA cycloadduct involving the aromatic ring of steroidal olefin 17 was not observed.
This LA-mediated Prins reaction can mechanistically be considered a P-AE reaction involving the C7–C8 double bond and the allylic H9 and H14 hydrogens of steroidal olefin 17, and the LA complex formed between Al(CH3)2Cl and formaldehyde 20. In this P-AE reaction, the hydrogen transfer process from the C9 and C14 carbons of steroidal olefin 17 to the carbonyl oxygen of the corresponding LA complex yields a homoallylic alcohol.
In order to investigate the possible competition between P-DA and P-AE reactions, the reaction between 2MBD 14 and LA complex BF3:formaldehyde 12 yielding the P-DA cycloadduct 15 and/or the P-AE adduct 16 are first studied within MEDT at the MPWB1K/6-311G(d,p) computational level (see Scheme 5). Then, the P-AE reaction of hexahydrophenanthrene (HPA) 21 with LA complex 12, as a reduced model of the Prins reaction experimentally carried out by Künzer et al. [18], as well as the P-DA reaction involving the aromatic ring of 21, are also studied (see Scheme 7).

2. Computational Methods

A recent analysis of the applicability of the B3LYP [19,20], MPWB1K [21], and M06-2X [22] functionals in the study of non-polar and polar cycloaddition reactions allowed selecting the MPWB1K functional as the most adequate one for the study of this type of organic reactions [15]. Consequently, DFT calculations were performed by using the MPWB1K functional together with the 6-311G(d,p) basis set [23]. Optimizations were carried out using the Berny analytical gradient optimization method [24,25]. The stationary points were characterized by frequency computations in order to verify that TSs have one and only one imaginary frequency. The intrinsic reaction coordinate (IRC) paths [26] were traced in order to check and obtain the energy profiles connecting each TS to the two associated minima of the proposed mechanism using the second order González-Schlegel integration method [27,28]. Solvent effects of 1,4-dioxane in the competitive P-DA and P-AE reactions of 2MBD 14 with LA complex BF3:formaldehyde 12 were taken into account by full optimization of the gas phase structures at the MPWB1K/6-311G(d,p) computational level using the polarizable continuum model (PCM) developed by Tomasi’s group [29,30] in the framework of the self-consistent reaction field (SCRF) [31,32,33]. As solvent effects do not produce remarkable changes neither in energies nor in geometries, solvent effects in the P-AE and P-DA reactions between HPA 21 and LA complex 12 were taken into account by single point energy calculations using the gas phase structures.
The GEDT was computed by the sum of the natural atomic charges (q), obtained by a natural population analysis [34,35] (NPA), of the atoms belonging to each framework (f) at the TSs; i.e., GEDT (f) = ∑ q ∈ f q ; f = nucleophile, electrophile. The sign indicates the direction of the electron density flux in such a manner that positive values mean a flux from the considered framework to the other one. Conceptual DFT (CDFT) global reactivity indices [36,37] and Parr functions [38] were computed using the equations given in reference 37. All computations were carried out with the Gaussian 09 suite of programs [39].
Topological analysis of the electron localization function [40] (ELF) was performed with the TopMod [41] package using the corresponding MPWB1K/6-311G(d,p) monodeterminantal wave functions and considering a cubical grid of step size of 0.1 Bohr, while quantum theory of atoms in molecules [42] (QTAIM) studies were performed with the Multiwfn [43] program. The molecular geometries and ELF basin attractor positions were visualized using the GaussView program [44], while the representation of the ELF basin isosurfaces was done by using the UCSF Chimera program [45].

3. Results and Discussion

The present MEDT study has been divided into four sections: in Section 3.1, an analysis of the CDFT reactivity indices at the ground state (GS) of the reagents involved in the competitive P-DA and P-AE reactions given in Scheme 5 and Scheme 7 is carried out; in Section 3.2, the competitive P-DA and P-AE reactions between 2MBD 14 and LA complex 12 are studied; in Section 3.3, the reaction paths associated to the P-DA and P-AE reactions between HPA 21 and LA complex 12 are explored and characterized; and finally, in Section 3.4, a comparative ELF topological analysis of the stationary points involved in the competitive P-DA and P-AE reactions between 2MBD 14 and LA complex 12 is performed.

3.1. Analysis of the CDFT Reactivity Indices at the GS of the Reagents

Numerous studies devoted to DA and AE reactions have shown that the analysis of the reactivity indices defined within CDFT [36,37] is a powerful tool to predict the reactivity in polar reactions. Consequently, in order to characterize the reactivity of s-cis and s-trans 2MBDs 14, HPA 21, formaldehyde 20, and LA complex 12 in polar reactions, the CDFT reactivity indices at the GS of the reagents were analysed. The global indices, namely, the electronic chemical potential, μ, chemical hardness, η, electrophilicity, ω, and nucleophilicity, N, are given in Table 1.
The electronic chemical potentials [46,47] μ of s-cis and s-trans 2MBDs 14 and HPA 21, μ = −3.30 (s-cis 14), −3.31 (s-trans 14) and −2.95 (21) eV, are significantly higher than that of LA complex 12, μ = −5.93 eV, indicating that along a polar reaction, the GEDT [14] will flux from these ethylene derivatives towards the electrophilic LA complex 12.
The electrophilicity ω [48] and nucleophilicity N [49] indices of formaldehyde 20 are ω = 1.45 and N = 1.81 eV, thus being classified as a strong electrophile within the electrophilicity scale [50] and as a moderate nucleophile within the nucleophilicity scale [51]. Note that within the group of strong electrophiles, there are experimentally stronger and weaker electrophiles. Thus, although formaldehyde 20 is classified as a strong electrophile within the electrophilicity scale, its electrophilic character is not strong enough to favor a polar reaction experimentally. Coordination of LA BF3 to the carbonyl oxygen of formaldehyde 20 notably increases the electrophilicity of the LA complex 12 to 2.69 eV. This strong electrophilic activation accounts for the participation of this carbonyl compound in polar reactions. On the other hand, the electrophilicity ω indices of the unsaturated hydrocarbons are 0.94 (s-cis 14), 0.99 (s-trans 14) and 0.71 (21) eV, 2MBD 14 being classified as a moderate electrophile and HPA 21 as a marginal electrophile, while their nucleophilicity N indices, 2.94 (s-cis 14), 3.07 (s-trans 14) and 3.11 (21) eV, allow the classification of s-cis 2MBD 14 on the borderline of strong nucleophiles, and s-trans 2MBD 14 and HPA 21 as strong nucleophiles. Consequently, along a polar reaction, it is expected that LA complex 12 will act as a strong electrophile, while these unsaturated hydrocarbons will act as strong nucleophiles.
By approaching nonsymmetric electrophilic/nucleophilic pairs along a polar process, the most favorable reactive pathway is that associated with the initial two-center interaction between the most electrophilic center of the electrophile and the most nucleophilic center of the nucleophile. Recently, Domingo et al. proposed the electrophilic P k + and nucleophilic P k − Parr functions [38], derived from the changes of spin electron density reached via the GEDT process from the nucleophile to the electrophile, as a powerful tool to study the local reactivity in polar and ionic processes. Accordingly, the electrophilic P k + Parr functions of LA complex 12, as well as the nucleophilic P k − Parr functions of unsaturated hydrocarbons s-trans 2MBD 14 and HPA 21, were analyzed in order to characterize the most electrophilic and nucleophilic centers of the species involved in the addition reaction of LA complex 12 to unsaturated hydrocarbons s-trans 2MBD 14 and HPA 21 (see Figure 1).
Analysis of the electrophilic P k + Parr functions at the reactive sites of LA complex 12 indicates that the carbonyl carbon, with a P k + value of 0.82, is the most electrophilic center of this species. On the other hand, analysis of the nucleophilic P k − Parr functions at the reactive sites of s-trans 2MBD 14 indicates that the C1 carbon, P k − = 0.54, is more nucleophilically activated than the C4 carbon, P k − = 0.43, although slightly (see Scheme 8 for nuclei labels). Finally, analysis of the nucleophilic P k − Parr functions at the reactive sites of HPA 21 shows at least six nucleophilically activated centers, the C7′ carbon, P k − = 0.22, being the most nucleophilic one. Consequently, it is expected that the P-AE reaction begins with the electrophilic attack of the carbonyl carbon of LA complex 12 on the C4′ or C7′ carbons of unsaturated hydrocarbons s-trans 2MBD 14 or HPA 21, respectively, in clear agreement with the experimental outcomes (see Scheme 6) [18].

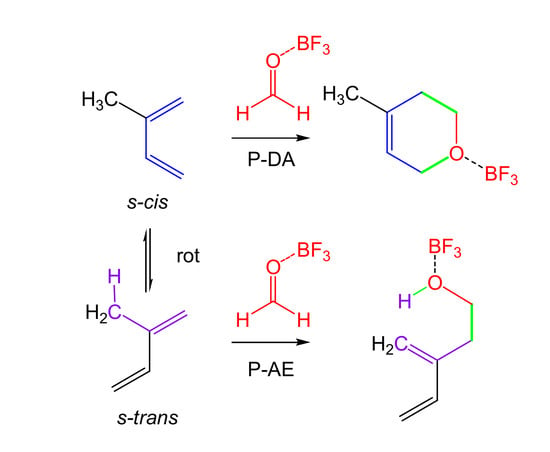
3.2. Comparative Study of the Competitive P-DA and P-AE Reactions between 2MBD 14 and LA Complex 12

In this section, the competitive P-DA and P-AE reaction paths associated with the BF3 LA-catalyzed reactions between 2MBD 14 and formaldehyde 20 are studied. For comparative purposes, the non-catalyzed DA and AE reactions between 2MBD 14 and formaldehyde 20 were also studied; the corresponding results are given in Supplementary Information. Analysis of the stationary points involved in the more favorable C1–C6 regioisomeric reaction paths associated with the two competitive P-DA and P-AE reaction paths shows that while the P-DA reaction path is characterized by a two-step mechanism similar to that found in the non-catalyzed reaction, the P-AE reaction path is characterized by a three-step mechanism (see Scheme 8). MPWB1K/6-311G(d,p) total and relative electronic energies, in gas phase and in dioxane, of the stationary points involved in the two competitive reaction paths are given in Table S4 in Supplementary Information. Relative energies in dioxane are given in Scheme 8.
Similar to the non-catalyzed process, the first step of both reaction paths is the formation of a molecular complex (MC) in which LA complex 12 is located above the plain of s-cis 2MBD 14 at a distance of ca. 2.6 Å. These species are found 6.2 (MC1) and 9.0 (MC2) kcal·mol−1 below the reagents. Interestingly, these MCs are more stable than those found in the non-catalyzed process presenting an O5–H8′ hydrogen bond (see Supplementary Information). From MC1, formation of cycloadduct 15 takes place along one elementary step via TS1-DA. The activation energy associated with TS1-DA from the more stable MC2 is only 3.6 kcal·mol−1; from MC2, formation of the final cycloadduct 15 being strongly exothermic by 36.0 kcal·mol−1.
Along the P-AE reaction path, the mechanism experiences a significant change: after the electrophilic attack of LA complex 12 on s-trans 2MBD 14, an intermediate IN2 associated with the formation of the C1–C6 single bond is found, thus making the formation of 16 from MC2 a stepwise process. From the more stable MC2, the activation energy associated to TS21-AE is 3.1 kcal·mol−1, formation of intermediate IN2 being endothermic by 1.3 kcal·mol−1. From IN2, the hydrogen transfer process via TS22-AE presents an activation energy of only 2.2 kcal·mol−1. From MC2, formation of the final adduct 16 is exothermic by 18.2 kcal·mol−1.
A comparative analysis of the activation energies associated with the non-catalyzed and catalyzed reactions allows obtaining two appealing conclusions: (i) the presence of the BF3 LA catalyst produces a large acceleration of both P-DA and P-AE reactions as a consequence of the strong electrophilic character of LA complex 12 (see Table 1) [13,16]. In fact, all the stationary points associated with the two catalyzed reaction paths are energetically found below the separated reagents; (ii) in the catalyzed process, TS22-AE is located 0.1 kcal·mol−1 below TS1-DA. Consequently, in dioxane, both P-DA and P-AE reactions become competitive in the catalyzed process.
In order to investigate how thermal corrections can modify the relative electronic energies, thermodynamic calculations were performed for the two competitive P-DA and P-AE reaction paths. Thermodynamic data are given in Table S5 of Supplementary Information, while the enthalpy profiles of the two competitive P-DA and P-AE reaction paths are represented in Figure 2. As this figure shows, MC1 and MC2 are minima on the enthalpy profile. On the other hand, analysis of the P-AE enthalpy profile emphasizes that TS21-AE, IN2 and TS22-AE present similar relative enthalpies. Interestingly, when the thermal corrections are considered, TS21-AE, which determines the rate-determining step (RDS) of the P-AE reaction path, is found 0.4 kcal·mol−1 below TS1-DA. This behavior indicates that, under kinetic control, adduct 16 resulting from the P-AE reaction will be formed to a slightly larger extent than cycloadduct 15 resulting from the P-DA reaction. The latter would be the product of a thermodynamic control of the reaction between 2MBD 14 and LA complex 12.
The gas phase geometries of the TSs involved in the competitive P-DA and P-AE reactions between 2MBD 14 and LA complex 12 are displayed in Figure 3. At TS1-DA, the large difference between the C–C and C–O distances, 0.95 Å, suggests that this TS may be related to a two-stage one-step mechanism [52], in which TS1-DA is associated to the electrophilic attack of the carbonyl C6 carbon of LA complex 12 on the C1 carbon of s-cis 2MBD 14. At TS21-AE, the short C1–C6 distance, 1.809 Å, indicates that at this TS the C1–C6 single bond may be already formed [14]. The C1–C6 and O5–H8 distances at intermediate IN2, are slightly shorter than those at TS21-AE. The geometrical similarity between TS21-AE and IN2 accounts for the notable flat PES found around these two species.
Finally, the electronic nature, i.e., polar character, of the competitive P-DA and P-AE reactions between 2MBD 14 and LA complex 12 was analyzed by computing the GEDT at the TSs and the intermediate. The values of the GEDT, fluxing from the butadiene to the LA:formaldehyde frameworks, are: 0.40 e at TS1-DA, 0.49 e at TS21-AE, 0.57 e at IN2. These high values allow establishing the high polar character of these reactions, which is a consequence of the strong nucleophilic character of 2MBD 14 and the strong electrophilic character of LA complex 12, and which accounts for the low computed activation energies [15]. Again, the higher GEDT found at TS21-AE than at TS1-DA is a consequence of the more advanced character of the former. The considerably stronger polar character of the reaction involving LA complex 12 than that involving formaldehyde 20 (see Supplementary Information) accounts for the lower activation energies of the former.

3.3. Study of the P-AE and P-DA Reactions between HPA 21 and LA Complex 12

Next, the reaction between HPA 21 and LA complex 12, as reduced compound models of the steroidal olefin 17 and the LA complex Al(CH3)2Cl:20 experimentally used by Künzer (see Scheme 6) [18], was studied. As HPA 21 presents three allylic hydrogens at the 6′, 9′ and 14′ positions, three different P-AE reaction paths are feasible. However, according to the analysis of the Parr functions (see Section 3.1), only the more favorable P-AE reaction paths involving the most nucleophilic C7′ carbon were studied. In addition, the P-DA reaction involving the aromatic ring of HPA 21 was also considered. Analysis of the stationary points involved in the more favorable C1–C7′ regioisomeric pathway associated to the two competitive P-AE reactions involving the H9′ or H14′ hydrogens indicates that they have different mechanisms. While the reaction path involving the abstraction of the tertiary 9′ hydrogen takes place through a two-step mechanism, that involving the abstraction of the secondary 14′ hydrogen takes place through a three-step mechanism (see Scheme 9). On the other hand, the P-DA reaction involving the aromatic ring takes place through a two-step mechanism. MPWB1K/6-311G(d,p) total and relative electronic energies, in gas phase and in dioxane, of the stationary points involved in the three reaction paths are given in Table S6 in Supplementary Information. Relative energies in dioxane are given in Scheme 9.
The two competitive P-AE reaction paths begin with the formation of two MCs found 8.2 (MC3) and 7.3 (MC4) kcal·mol−1 below the separated reagents, which are found in thermodynamic equilibrium. The activation energy associated with the P-AE reaction path via TS3-AE is 7.3 kcal·mol−1; formation of the corresponding homoallylic alcohol 22 being exothermic by 19.7 kcal·mol−1. A more complex mechanism is found for the formation of homoallylic alcohol 23; from MC4, the P-AE reaction path takes place via a two-step mechanism. After formation of MC4, the P-AE reaction begins by the electrophilic attack of the carbonyl carbon of LA complex 12 on the C7′ carbon of HPA 21, yielding intermediate IN4 via TS41-AE. From the most stable MC3, the activation energy associated to this step is 8.2 kcal·mol−1, formation of intermediate IN4 being endothermic by 6.2 kcal·mol−1. The last step is the hydrogen transfer from the C14′ carbon of the HPA framework to the carbonyl oxygen of the formaldehyde one, yielding the final homoallylic alcohol 23. The activation energy associated to this hydrogen transfer step is 0.9 kcal·mol−1, formation of the final homoallylic alcohol 23 being exothermic by 25.4 kcal·mol−1.
The P-DA reaction path begins with the formation of MC5, which is found 6.3 kcal·mol−1 below the separated reagents. From this MC, formation of cycloadduct 24 takes place in one elementary step via TS5-DA. From the most stable MC3, the activation energy associated to this P-DA reaction is 22.8 kcal·mol−1, the reaction being endothermic by 12.1 kcal·mol−1.
Some appealing conclusions can be drawn from the energy results given in Scheme 9: (i) these LA-catalyzed Prins (AE) reactions present very low activation energies, less than 8.2 kcal·mol−1, in agreement with the low temperature used in the reaction, −5 °C [18]; (ii) in dioxane, TS3-AE is slightly more stabilized than TS41-AE and, consequently, formation of adduct 22 is slightly more favorable than formation of 23, in agreement with the experimental results (see Scheme 6); and finally, (iii) the P-DA reaction involving the participation of the aromatic ring presents a very high activation energy, similar to that found in the non-catalyzed process, making this P-DA reaction non-competitive with the P-AE reactions. This behavior is a consequence of the difficulty of the aromatic ring to participate as diene or ethylene in P-DA reactions [53]. Note that the activation energy associated to this P-DA reaction is 17.0 kcal·mol−1 higher than that involving 2MBD 14.
Thermodynamic data for the competitive reaction paths between HPA 21 and LA complex 12 are given in Table S7 of Supplementary Information, while the enthalpy profiles of the three competitive reaction paths are represented in Figure 4. As can be seen, the three MCs are minima on the enthalpy profile. The enthalpy profiles associated to the two competitive P-AE reactions show that TS3-AE is located 1.9 kcal·mol−1 below TS41-AE, in agreement with the preferential formation of homoallylic alcohols 18 (see Scheme 6) [18]. Note that the first step is the RDS of the stepwise AE reaction. On the other hand, the high activation enthalpy associated with TS5-DA makes this reaction path non-competitive. Formation of homoallylic alcohols 22 and 23 is strongly exothermic and, consequently, irreversible, while formation of the DA cycloadduct 24 is endothermic and, therefore, reversible. Thus, the DA reaction is both kinetically and thermodynamically unfavorable. Finally, a comparative analysis of the enthalpy profiles associated to the competitive P-AE reactions given in Figure 2 and Figure 4 shows a great similitude, supporting the reaction between 2MBD 14 and LA complex 12 as a good computational model of the reaction between HPA 21 and LA complex 12.
The gas phase geometries of the TSs involved in the P-DA and P-AE reactions between HPA 21 and LA complex 12 are displayed in Figure 5. At TS3-AE, the lengths of the C1–C7′, C9′–H and O2–H indicate that this TS is mainly associated to the hydrogen transfer process; note that at intermediate IN4, the length of the C1–C7′ bond indicates that it is already formed [14]. At the stepwise P-AE reaction path, the C1–C7′ and O2–H distances at TS41-AE, 1.901 and 2.302 Å, respectively, indicate that this TS is associated to the formation of the C–C single bond. At intermediate IN4, the C1–C7′ bond length, 1.649 Å, indicates that this C–C single bond has practicality been formed. Finally, at TS42-AE, the C14′–H and O2–H lengths indicate that, similar to TS42-AE, this TS is mainly associated to the rupture of the C14′–H bond. Finally, at TS5-DA, the C1–C4′ and O2–C1′ lengths, 1.655 and 2.037 Å, respectively, reveal the very advanced character of this unfavorable TS, in which the C1–C4′ single bond has already been formed.
Finally, the electronic nature of the P-AE and P-DA reactions between HPA 21 and LA complex 12 was analyzed by computing the GEDT at the TSs and the intermediate. The values of the GEDT, fluxing from the HPA to the BF3:formaldehyde frameworks, along the P-AE reactions are 0.65 e (TS3-AE), 0.44 e (TS41-AE) and 0.64 e (IN4). These very high values allow establishing the strong polar character of these P-AE reactions, which accounts for the low computed activation energies. On the other hand, along the P-DA reaction, the value of the GEDT at TS5-DA is 0.52 e. Note that despite this very high GEDT value, the unfavorable activation energy associated to this TS is the consequence of the loss of the phenyl aromaticity [53]. The high polar character of these P-DA and P-AE reactions is the consequence of the strong nucleophilic character of HPA 21 and the strong electrophilic character of LA complex 12.

3.4. Comparative ELF Analysis of the Competitive Polar P-DA and P-AE Reactions between 2MBD 14 and LA Complex 12. Origin of the Pseudocyclic Selectivity

In order to compare the C–C bond-formation process along the competitive P-DA and P-AE reactions between 2MBD 14 and LA complex 12, a topological analysis of the ELF of the stationary points involved in the two reaction paths was carried out. The complete ELF analysis is given in Section 2 of the Supplementary Material.
Some appealing conclusions can be drawn from this comparative ELF analysis: (i) TS1-DA and TS21-EA present a great electronic similarity. The only topological difference between these TSs is the presence of the V(C1) monosynaptic basin with a population of 0.63 e at TS1-DA and the presence of the V(C1,C6) disynaptic basin with a population of 0.94 e at TS21-AE. Note that the V(C1) monosynaptic basin is demanded for the subsequent formation of the V(C1,C6) disynaptic basin. This topological difference, which was supported by a QTAIM analysis of the two TSs (see Supplementary Information), is a consequence of the more advanced character of the latter TS; (ii) consequently, TS1-DA and TS21-EA are a pair of stereoisomeric TSs with a very similar electronic structure (see Figure 6). This behavior accounts for their similar electronic energies; (iii) at IN2, while the new C1–C6 single bond has reached a population of 1.22 e, the population of the C7–H8 bond remains 1.86 e. Consequently, the first step of the P-AE reaction path is associated only to the formation of the C1–C6 single bond, in agreement with the geometrical analysis; and finally (iv) at TS22-AE, while the new C1–C6 single bond continues increasing its population to 1.58 e, the population of the C7–H8 bond still is 1.63 e, indicating that the rupture of the C7–H8 bond has not yet begun at this TS.
A representation of the geometries of the competitive TS1-DA and TS21-AE along the formation of the first C1–C5 single bond shows that they are a pair of conformational (stereoisomeric) TSs resulting from the C2–C3 and C1–C5 single bond rotation, with a very similar electronic structure (see Figure 7). This behavior makes it possible to explain their similar electronic energy, and consequently, the competitiveness found between the DA and AE reaction paths.
As the two conformational TSs are associated with the nucleophilic attack of the C1 carbon of 2MBD 14 on the carbonyl C6 carbon of LA complex 12, the two competitive reaction paths are differentiated after passing these TSs; while the P-DA reaction path yields cycloadduct 15 through the subsequent ring closure, the P-AE reaction path stops at intermediate IN2, which is able to take away a hydrogen of the neighboring methyl group with a very low activation energy yielding the final adduct 16.
A similar finding was found in the competitive formation of the [3 + 2] or [2 + 4] cycloadducts 26 and 27 in the BF3 LA-catalyzed reaction between Cp 1 and methyl glyoxylate oxime 25 (see Scheme 10) [54]. This reaction was characterized by the nucleophilic attack of Cp 1 onto the carbon of the corresponding BF3:nitrone complex. After passing the competitive stereoisomeric TSs, the subsequent ring closure at the end of the reaction allows the formation of the [3 + 2] or [2 + 4] cycloadducts 26 and 27 [55]. These competitive cycloaddition reactions, which take place through non-concerted cyclic TSs, are classified as pseudocyclic reactions [11].
In 1970, Houk et al. introduced the concept of “periselectivity” as the selective formation of one of the thermally allowed pericyclic reaction products [56,57]. However, as the pericyclic mechanism has been recently ruled out [11], the term “periselectivity” has no sense. Therefore, in order to provide a more precise definition of the selectivity in the formation of structural isomers resulting from competitive pseudocyclic reactions, the “pseudocyclic selectivity” concept is established herein. Thus, the unexpected formation of the [3 + 2] cycloadduct 26 in Scheme 10, as well as the preferential formation of the P-AE adduct 16 versus the P-DA cycloadduct 15 with the increased polar character of the reaction, are examples of the proposed pseudocyclic selectivity. However, note that formation of the P-AE adducts 22 and 23 versus formation of the P-DA cycloadduct 24, which come from the electrophilic attack of LA complex 12 to different positions of HPA 21, is related with the chemoselectivity of this Prins reaction.

4. Conclusions

The BF3 LA-catalyzed P-DA and P-AE reactions of 2MBD 14, having an allylic hydrogen, with formaldehyde 20 have been studied within MEDT at the MPWB1K/6-311G(d,p) computational level. In the absence of the LA catalyst, both reactions present very high activation energies. Coordination of the BF3 LA to the oxygen of formaldehyde 20 drastically accelerates both reactions as a consequence of the high electrophilic character of the formed LA complex 12, which favors these reactions to take place with very low activation enthalpy, less than 2.2 kcal·mol−1, and very high polar character; the P-AE reaction being slightly favored as a consequence of the larger polar character of TS21-AE than TS1-DA. The P-AE reaction between s-trans 2MBD 14 and LA complex 12 takes place through a stepwise mechanism, in which the hydrogen transfer process takes place after the formation of the first C–C single bond. However, the very similar energies found for the TSs and intermediate makes this finding experimentally irrelevant.
The Prins reaction between HPA 21 and LA complex 12 has also been studied as a computational model of the reaction experimentally reported by Künzer using steroidal olefin 17 [18]. The corresponding MEDT study, which allows explaining the experimental outcomes, supports 2MBD 14 as a computational model for this comparative study of the competitiveness between P-DA and P-AE reactions. For the reaction between HPA 21 and LA complex 12, the corresponding P-DA reaction presents very high activation energy as the consequence of the aromatic character of the diene framework, lost along the cycloaddition reaction. For the two most favorable competitive P-AE reactions, two different mechanisms with low activation energies have been found.
Finally, an ELF topological analysis of the stationary points involved in the P-DA reaction and the P-AE reaction of s-trans 2MBD 14 with LA complex 12 allows explaining the competitive character of these polar reactions. Both TS1-DA and TS21-AE, which are associated to the nucleophilic attack of the C1 carbon of 2MBD 14 on the carbonyl C6 carbon of LA complex 12, form a pair of stereoisomeric TSs with a very similar electronic structure [54].
The present MEDT study allows establishing the competitiveness of the P-AE reactions in P-DA reactions when the diene substrate possesses, at least, one allylic hydrogen. This competitiveness, which is a consequence of the conformational relationship between the TSs involved in the RDSs of the P-DA and P-AE reactions, is increased with the polar character of the reaction; thus, while in low polar reactions formation of the corresponding DA cycloadduct is kinetically and thermodynamically favored, in highly polar reactions, formation of the corresponding P-AE adduct may be kinetically favored. The selectivity in the formation of P-DA cycloadducts and P-AE adducts such as 15 and 16, which constitute a pair of structural isomers coming from two stereoisomeric TSs, has been defined herein as pseudocyclic selectivity.

Supplementary Materials

The following are available online, Comparative study of the DA and AE reactions between 2MBD 14 and formaldehyde 20. ELF topological analysis of the competitive P-DA and P-AE reactions between 2MBD 14 and LA complex 12. QTAIM analysis of the electron density in the C1–C6 region at TS1-DA and TS21-AE. Tables with the MPWB1K/6-311G(d,p) total and relative energies, in gas phase and in dioxane, and with thermodynamic data of the stationary points involved in the competitive P-DA and P-AE reactions between 2-methylbutadiene 14 and LA complex 12. Tables with the MPWB1K/6-311G(d,p) total and relative energies, in gas phase and in dioxane, as well as thermodynamic data, of the stationary points involved in the P-DA and P-AE reactions between HPA 21 and LA complex 12.

Author Contributions

L.R.D. headed the subject and he and M.R.-G. and P.P. performed the calculations, collected the literature and participated in the writing of the manuscript.

Funding

Ministry of Economy and Competitiveness (MINECO) of the Spanish Government, project CTQ2016-78669-P (AEI/FEDER, UE) and Fondecyt (Chile) grant 1180348.

Acknowledgments

This research was supported by the Ministry of Economy and Competitiveness (MINECO) of the Spanish Government, project CTQ2016-78669-P (AEI/FEDER, UE) and Fondecyt (Chile) grant 1180348. L.R.D. thanks Fondecyt for continuous support through Cooperación Internacional. M.R.-G. also thanks MINECO for a post-doctoral contract cofinanced by the European Social Fund (BES-2014-068258).

Conflicts of Interest

The author declares no conflicts of interest.

References

  1. Diels, O.; Alder, K. Synthesen in der hydroaromatischen Reihe. Justus Liebigs Ann. Chem. 1928, 460, 98–122. [Google Scholar] [CrossRef]
  2. Carruthers, W. Some Modern Methods of Organic Synthesis, 2nd ed.; Cambridge University Press: Cambridge, UK, 1978. [Google Scholar]
  3. Carruthers, W. Cycloaddition Reactions in Organic Synthesis; Pergamon Press: Oxford, UK, 1990. [Google Scholar]
  4. Alder, K.; Pascher, F.; Schmitz, A. Absorption of maleic acid-anhydride and azodicarbon acid-ester in simple unsaturated carbohydrogens. Information on the substitution processes in the allyl position. Ber. Dtsch. Chem. Ges. 1943, 76, 27–53. [Google Scholar] [CrossRef]
  5. Mikami, K.; Shimizu, M. Asymmetric ene reactions in organic synthesis. Chem. Rev. 1992, 92, 1021–1050. [Google Scholar] [CrossRef]
  6. Nahm, S.H.; Cheng, H.M. Transition-state geometry and stereochemistry of the ene reaction between olefins and maleic anhydride. J. Org. Chem. 1986, 51, 5093–5100. [Google Scholar] [CrossRef]
  7. Carey, F.A.; Sundberg, R.J. Advanced Organic Chemistry. Part A: Strucutre and Mechanisms, 5th ed.; Springer: New York, NY, USA, 2007. [Google Scholar]
  8. Fleming, I. Molecular Orbitals and Organic Chemical Reaction; John Wiley & Sons: West Sussex, UK, 2009. [Google Scholar]
  9. Woodward, R.B.; Hoffmann, R. The conservation of orbital symmetry. Angew. Chem. Int. Ed. Engl. 1969, 8, 781–853. [Google Scholar] [CrossRef]
  10. Domingo, L.R. Molecular electron density theory: A modern view of reactivity in organic chemistry. Molecules 2016, 21, 1319. [Google Scholar] [CrossRef] [PubMed]
  11. Domingo, L.R.; Ríos-Gutiérrez, M.; Silvi, B.; Pérez, P. The mysticism of pericyclic reactions: A contemporary rationalisation of organic reactivity based on electron density analysis. Eur. J. Org. Chem. 2018, 2018, 1107–1120. [Google Scholar] [CrossRef]
  12. Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
  13. Domingo, L.R.; Sáez, J.A. Understanding the mechanism of polar Diels-Alder reactions. Org. Biomol. Chem. 2009, 7, 3576–3583. [Google Scholar] [CrossRef] [PubMed]
  14. Domingo, L.R. A new C-C bond formation model based on the quantum chemical topology of electron density. RSC Adv. 2014, 4, 32415–32428. [Google Scholar] [CrossRef]
  15. Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. How does the global electron density transfer diminish activation energies in polar cycloaddition reactions? A Molecular Electron Density Theory study. Tetrahedron 2017, 73, 1718–1724. [Google Scholar] [CrossRef]
  16. Domingo, L.R.; Aurell, M.J.; Pérez, P. Understanding the polar mechanism of the ene reaction. A DFT study. Org. Biomol. Chem. 2014, 12, 7581–7590. [Google Scholar] [CrossRef] [PubMed]
  17. Arundale, E.; Mikeska, L.A. The olefin-aldehyde condensation. The Prins reaction. Chem. Rev. 1952, 51, 505–555. [Google Scholar] [CrossRef]
  18. Künzer, H.; Sauer, G.; Wiechert, R. Stereocontrolled derivatization of 3-methoxyestra-1,3,5(10), n-tetraenes via lewis acid promoted prins reactions, (n = 7; 8(9)). Tetrahedron Lett. 1991, 32, 743–746. [Google Scholar] [CrossRef]
  19. Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
  20. Becke, A.D. Density-functional thermochemistry. The role of exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
  21. Zhao, Y.; Truhlar, D.G. Hybrid meta density functional theory methods for thermochemistry, thermochemical kinetics, and noncovalent Interactions: The MPW1B95 and MPWB1K models and comparative assessments for hydrogen bonding and van der Waals interactions. J. Phys. Chem. A 2004, 108, 6908–6918. [Google Scholar] [CrossRef]
  22. Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinectics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
  23. Hehre, M.J.; Radom, L.; Schleyer, P.V.R.; Pople, J. Ab initio Molecular Orbital Theory; Wiley: New York, NY, USA, 1986. [Google Scholar]
  24. Schlegel, H.B. Optimization of equilibrium geometries and transition structures. J. Comput. Chem. 1982, 3, 214–218. [Google Scholar] [CrossRef]
  25. Schlegel, H.B. In Modern Electronic Structure Theory; Yarkony, D.R., Ed.; World Scientific Publishing: Singapore, 1994. [Google Scholar]
  26. Fukui, K. Formulation of the reaction coordinate. J. Phys. Chem. 1970, 74, 4161–4163. [Google Scholar] [CrossRef]
  27. González, C.; Schlegel, H.B. Reaction path following in mass-weighted internal coordinates. J. Phys. Chem. 1990, 94, 5523–5527. [Google Scholar] [CrossRef]
  28. González, C.; Schlegel, H.B. Improved algorithms for reaction path following: Higher-order implicit algorithms. J. Chem. Phys. 1991, 95, 5853–5860. [Google Scholar] [CrossRef]
  29. Tomasi, J.; Persico, M. Molecular interactions in solution: And overview of methods based on continuous distributions of the solvent. Chem. Rev. 1994, 94, 2027–2094. [Google Scholar] [CrossRef]
  30. Simkin, B.I.; Sheikhet, I.I. Quantum Chemical and Statistical Theory of Solutions—Computational Approach; Ellis Horwood: London, UK, 1995. [Google Scholar]
  31. Cossi, M.; Barone, V.; Cammi, R.; Tomasi, J. Ab nitio Study of Solvated Molecules: A New Implementation of the Polarizable Continuum Model. Chem. Phys. Lett. 1996, 255, 327–335. [Google Scholar] [CrossRef]
  32. Cances, E.; Mennucci, B.; Tomasi, J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. [Google Scholar] [CrossRef]
  33. Barone, V.; Cossi, M.; Tomasi, J. Geometry optimization of molecular structures in solution by the polarizable continuum model. J. Comput. Chem. 1998, 19, 404–417. [Google Scholar] [CrossRef]
  34. Reed, A.E.; Weinstock, R.B.; Weinhold, F. Natural population analysis. J. Chem. Phys. 1985, 83, 735–746. [Google Scholar] [CrossRef]
  35. Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
  36. Geerlings, P.; De Proft, F.; Langenaeker, W. Conceptual density functional theory. Chem. Rev. 2003, 103, 1793–1873. [Google Scholar] [CrossRef] [PubMed]
  37. Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. Applications of the Conceptual density functional indices to organic chemistry reactivity. Molecules 2016, 21, 748. [Google Scholar] [CrossRef] [PubMed]
  38. Domingo, L.R.; Pérez, P.; Sáez, J.A. Understanding the local reactivity in polar organic reactions through electrophilic and nucleophilic Parr functions. RSC Adv. 2013, 3, 1486–1494. [Google Scholar] [CrossRef] [Green Version]
  39. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision A. 02; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
  40. Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular-systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
  41. Noury, S.; Krokidis, X.; Fuster, F.; Silvi, B. Computational tools for the electron localization function topological analysis. Comput. Chem. 1999, 23, 597–604. [Google Scholar] [CrossRef]
  42. Bader, R.F.W. Atoms in Molecules. A Quantum Theory; Claredon Press: Oxford, UK, 1990. [Google Scholar]
  43. Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
  44. Dennington, R.; Keth, T.; Millam, J. GaussView, Version 3; Semichem Inc.: Shawnee Mission, KS, USA, 2009. [Google Scholar]
  45. Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. USCF Chimera—A visualization system for exploratory research and analysis. J. Comput. Chem. 2004, 25, 1605–1612. [Google Scholar] [CrossRef] [PubMed]
  46. Parr, R.G.; Pearson, R.G. Absolute hardness: Companion parameter to absolute electronegativity. J. Am. Chem. Soc. 1983, 105, 7512. [Google Scholar] [CrossRef]
  47. Parr, R.G.; Yang, W. Density Functional Theory of Atoms and Molecules; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
  48. Parr, R.G.; Szentpaly, L.V.; Liu, S. Electrophilicity index. J. Am. Chem. Soc. 1999, 121, 1922–1924. [Google Scholar] [CrossRef]
  49. Domingo, L.R.; Chamorro, E.; Pérez, P. Understanding the reactivity of captodative ethylenes in polar cycloaddition reactions. A theoretical study. J. Org. Chem. 2008, 73, 4615–4624. [Google Scholar] [CrossRef] [PubMed]
  50. Domingo, L.R.; Aurell, M.J.; Pérez, P.; Contreras, R. Quantitative characterization of the global electrophilicity power of common diene/dienophile pairs in Diels-Alder reactions. Tetrahedron 2002, 58, 4417–4423. [Google Scholar] [CrossRef]
  51. Jaramillo, P.; Domingo, L.R.; Chamorro, E.; Pérez, P. A further exploration of a nucleophilicity index based on the gas-phase ionization potentials. J. Mol. Struct. THEOCHEM 2008, 865, 68–72. [Google Scholar] [CrossRef]
  52. Domingo, L.R.; Ríos-Gutiérrez, M.; Sáez, J.A. Unravelling the mechanism of the ketene-imine Staudinger reaction. An ELF quantum topological analysis. RSC Adv. 2015, 5, 37119–37129. [Google Scholar] [CrossRef] [Green Version]
  53. Domingo, L.R.; Pérez, P.; Ortega, D.E. Why Do Five-Membered Heterocyclic Compounds Sometimes Not Participate in Polar Diels–Alder Reactions? J. Org. Chem. 2013, 78, 2462–2471. [Google Scholar] [CrossRef] [PubMed]
  54. Sousa, C.A.D.; Vale, M.L.C.; Garcia-Mera, X.; Rodríguez-Borges, J.E. 1,3-versus 1,4-[π4+π2] Cycloadditions between methyl glyoxylate oxime and cyclopentadiene or cyclopentene. Tetrahedron 2012, 68, 1682–1887. [Google Scholar] [CrossRef]
  55. Rhyman, L.; Ramasami, P.; Joule, J.A.; Sáez, J.A.; Domingo, L.R. Understanding the formation of [3 + 2] and [2 + 4] cycloadducts in the Lewis acid catalysed reaction between methyl glyoxylate oxime and cyclopentadiene: A theoretical study. RSC Adv. 2013, 3, 447–457. [Google Scholar] [CrossRef]
  56. Houk, K.N.; Luskus, L.J.; Bhacca, N.S. Novel double [6 + 4] cycloaddition of tropone to dimethylfulvene. J. Am. Chem. Soc. 1970, 92, 6392–6394. [Google Scholar] [CrossRef]
  57. Houk, K.N.; Sims, J.; Watts, C.R.; Luskus, L.J. Origin of reactivity, regioselectivity, and periselectivity in 1,3-dipolar cycloadditions. J. Am. Chem. Soc. 1973, 95, 7301–7315. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds are not available from the authors.
Molecules 23 01913 sch001 550
Scheme 1. Diels-Alder reaction between cyclopentadiene 1 and maleic anhydride 2 yielding the bicyclic adduct 3 [1].
Scheme 1. Diels-Alder reaction between cyclopentadiene 1 and maleic anhydride 2 yielding the bicyclic adduct 3 [1].
Molecules 23 01913 sch001
Molecules 23 01913 sch002 550
Scheme 2. Alder-ene reaction of propene 4 with maleic anhydride 2 yielding adduct 5 [6].
Scheme 2. Alder-ene reaction of propene 4 with maleic anhydride 2 yielding adduct 5 [6].
Molecules 23 01913 sch002
Molecules 23 01913 sch003 550
Scheme 3. Series of polar Diels-Alder reactions between Cp 1 and ethylene derivatives 8 of increased electrophilicity.
Scheme 3. Series of polar Diels-Alder reactions between Cp 1 and ethylene derivatives 8 of increased electrophilicity.
Molecules 23 01913 sch003
Molecules 23 01913 sch004 550
Scheme 4. Alder-ene reactions of isobutene 10 with ethylene 7 or Lewis acids complex BF3:formaldehyde 12.
Scheme 4. Alder-ene reactions of isobutene 10 with ethylene 7 or Lewis acids complex BF3:formaldehyde 12.
Molecules 23 01913 sch004
Molecules 23 01913 sch005 550
Scheme 5. Competitive P-DA and P-AE reactions between the s-trans and s-cis conformations of 2-methyl-1,3-butadiene 14 and Lewis acid complex 12, respectively.
Scheme 5. Competitive P-DA and P-AE reactions between the s-trans and s-cis conformations of 2-methyl-1,3-butadiene 14 and Lewis acid complex 12, respectively.
Molecules 23 01913 sch005
Molecules 23 01913 sch006 550
Scheme 6. Prins reaction of the steroidal olefin 17 [18].
Scheme 6. Prins reaction of the steroidal olefin 17 [18].
Molecules 23 01913 sch006
Molecules 23 01913 sch007 550
Scheme 7. Competitive polar Diels-Alder and polar Alder-ene reactions between hexahydrophenanthrene 21 and Lewis acid complex BF3:formaldehyde 12.
Scheme 7. Competitive polar Diels-Alder and polar Alder-ene reactions between hexahydrophenanthrene 21 and Lewis acid complex BF3:formaldehyde 12.
Molecules 23 01913 sch007
Molecules 23 01913 g001 550
Figure 1. Three-dimensional representations of the Mulliken atomic spin densities of radical anion 12− and radical cations s-trans 2MBD 14+ and HPA 21+, together with the electrophilic P k + and nucleophilic P k − Parr functions of LA complex 12 and unsaturated hydrocarbons s-trans 2MBD 14 and HPA 21.
Figure 1. Three-dimensional representations of the Mulliken atomic spin densities of radical anion 12− and radical cations s-trans 2MBD 14+ and HPA 21+, together with the electrophilic P k + and nucleophilic P k − Parr functions of LA complex 12 and unsaturated hydrocarbons s-trans 2MBD 14 and HPA 21.
Molecules 23 01913 g001
Molecules 23 01913 sch008 550
Scheme 8. Competitive polar Diels-Alder and polar Alder-ene reaction paths associated to the reaction of 2-methyl-1,3-butadiene 14 and Lewis acid complex 12 along the more favorable C1–C6 regioisomeric pathways. Relative energies in dioxane, in kcal·mol−1, are given in parentheses.
Scheme 8. Competitive polar Diels-Alder and polar Alder-ene reaction paths associated to the reaction of 2-methyl-1,3-butadiene 14 and Lewis acid complex 12 along the more favorable C1–C6 regioisomeric pathways. Relative energies in dioxane, in kcal·mol−1, are given in parentheses.
Molecules 23 01913 sch008
Molecules 23 01913 g002 550
Figure 2. MPWB1K/6-311G(d,p) enthalpy profiles, kcal·mol−1, computed at −5 °C in dioxane, of the competitive P-DA and P-AE reaction paths associated with the reaction of 2MBD 14 with LA complex 12 along the more favorable C1–C6 regioisomeric pathways.
Figure 2. MPWB1K/6-311G(d,p) enthalpy profiles, kcal·mol−1, computed at −5 °C in dioxane, of the competitive P-DA and P-AE reaction paths associated with the reaction of 2MBD 14 with LA complex 12 along the more favorable C1–C6 regioisomeric pathways.
Molecules 23 01913 g002
Molecules 23 01913 g003 550
Figure 3. MPWB1K/6-311G(d,p) gas phase optimized geometries of the TSs and intermediate involved in the more favorable C1–C6 regioisomeric pathways associated to the competitive P-DA and P-AE reactions between 2MBD 14 and LA complex 12. Distances are given in angstroms, Å.
Figure 3. MPWB1K/6-311G(d,p) gas phase optimized geometries of the TSs and intermediate involved in the more favorable C1–C6 regioisomeric pathways associated to the competitive P-DA and P-AE reactions between 2MBD 14 and LA complex 12. Distances are given in angstroms, Å.
Molecules 23 01913 g003
Molecules 23 01913 sch009 550
Scheme 9. Competitive polar Alder-ene reactions between hexahydrophenanthrene 21 and Lewis acid complex 12 along the more favorable C1–C7′ regioisomeric pathway. The experimentally not observed polar Diels-Alder reaction involving the aromatic ring is also included. Relative energies in dioxane, in kcal·mol−1, are given in parentheses.
Scheme 9. Competitive polar Alder-ene reactions between hexahydrophenanthrene 21 and Lewis acid complex 12 along the more favorable C1–C7′ regioisomeric pathway. The experimentally not observed polar Diels-Alder reaction involving the aromatic ring is also included. Relative energies in dioxane, in kcal·mol−1, are given in parentheses.
Molecules 23 01913 sch009
Molecules 23 01913 g004 550
Figure 4. MPWB1K/6-311G(d,p) enthalpy profiles, kcal·mol−1, computed at −5 °C in dioxane, of the competitive P-DA and P-AE reaction paths associated with the reaction of between HPA 21 and LA complex 12.
Figure 4. MPWB1K/6-311G(d,p) enthalpy profiles, kcal·mol−1, computed at −5 °C in dioxane, of the competitive P-DA and P-AE reaction paths associated with the reaction of between HPA 21 and LA complex 12.
Molecules 23 01913 g004
Molecules 23 01913 g005a 550Molecules 23 01913 g005b 550
Figure 5. MPWB1K/6-311G(d,p) gas phase optimized geometries of the TSs and intermediate involved in the P-AE and P-DA reactions between HPA 21 and LA complex 12. Distances are given in angstroms, Å.
Figure 5. MPWB1K/6-311G(d,p) gas phase optimized geometries of the TSs and intermediate involved in the P-AE and P-DA reactions between HPA 21 and LA complex 12. Distances are given in angstroms, Å.
Molecules 23 01913 g005aMolecules 23 01913 g005b
Molecules 23 01913 g006 550
Figure 6. Attractor positions of the ELF valence basins for the TS involved in the P-DA reaction, TS1-DA, and TSs and intermediate involved in the P-AE reaction, TS21-AE, IN2 and TS22-AE, between 2MBD 14 and LA complex 12. The electron populations, in average number of electrons, e, are given in brackets.
Figure 6. Attractor positions of the ELF valence basins for the TS involved in the P-DA reaction, TS1-DA, and TSs and intermediate involved in the P-AE reaction, TS21-AE, IN2 and TS22-AE, between 2MBD 14 and LA complex 12. The electron populations, in average number of electrons, e, are given in brackets.
Molecules 23 01913 g006
Molecules 23 01913 g007 550
Figure 7. A view of TS1-DA and TS21-AE along the formation of the first C1–C5 single bonds. They are a pair of stereoisomeric TSs resulting from the C2–C3 and C1–C5 bond rotations.
Figure 7. A view of TS1-DA and TS21-AE along the formation of the first C1–C5 single bonds. They are a pair of stereoisomeric TSs resulting from the C2–C3 and C1–C5 bond rotations.
Molecules 23 01913 g007
Molecules 23 01913 sch010 550
Scheme 10. Lewis acid catalyzed reaction between cyclopentadiene 1 and methyl glyoxylate oxime 25 yielding the [3 + 2] or [2 + 4] cycloadducts 26 and 27.
Scheme 10. Lewis acid catalyzed reaction between cyclopentadiene 1 and methyl glyoxylate oxime 25 yielding the [3 + 2] or [2 + 4] cycloadducts 26 and 27.
Molecules 23 01913 sch010
Table
Table 1. B3LYP/6-31G(d) electronic chemical potential (μ), chemical hardness (η), global electrophilicity (ω) and global nucleophilicity (N), in eV, of s-cis and s-trans 2MBDs 14, HPA 21, formaldehyde 20 and LA complex 12.
Table 1. B3LYP/6-31G(d) electronic chemical potential (μ), chemical hardness (η), global electrophilicity (ω) and global nucleophilicity (N), in eV, of s-cis and s-trans 2MBDs 14, HPA 21, formaldehyde 20 and LA complex 12.
μηωN
12−5.936.522.69−0.07
20−4.236.161.451.81
s-trans14−3.315.500.993.07
s-cis14−3.305.770.942.94
21−2.956.100.713.11

Share and Cite

MDPI and ACS Style

Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. A Molecular Electron Density Theory Study of the Competitiveness of Polar Diels–Alder and Polar Alder-ene Reactions. Molecules 2018, 23, 1913. https://doi.org/10.3390/molecules23081913

AMA Style

Domingo LR, Ríos-Gutiérrez M, Pérez P. A Molecular Electron Density Theory Study of the Competitiveness of Polar Diels–Alder and Polar Alder-ene Reactions. Molecules. 2018; 23(8):1913. https://doi.org/10.3390/molecules23081913

Chicago/Turabian Style

Domingo, Luis R., Mar Ríos-Gutiérrez, and Patricia Pérez. 2018. "A Molecular Electron Density Theory Study of the Competitiveness of Polar Diels–Alder and Polar Alder-ene Reactions" Molecules 23, no. 8: 1913. https://doi.org/10.3390/molecules23081913

APA Style

Domingo, L. R., Ríos-Gutiérrez, M., & Pérez, P. (2018). A Molecular Electron Density Theory Study of the Competitiveness of Polar Diels–Alder and Polar Alder-ene Reactions. Molecules, 23(8), 1913. https://doi.org/10.3390/molecules23081913

Article Metrics

Back to TopTop