1. Introduction
Glasses are amorphous materials lacking the periodic atomic arrangement typical for crystalline substances. Structurally, they resemble supercooled liquids but behave mechanically like solids.
Figure 1 shows the specific volume or enthalpy as a function of temperature for a typical glass-forming liquid. Upon slow cooling from high temperatures, a liquid may crystallize at T
m forming a stable crystalline material. However, if the cooling through this temperature range is fast enough to avoid nucleation and subsequent crystal growth, a metastable supercooled liquid state is attained.
When a supercooled liquid is cooled by a cooling rate of q
+1 to lower temperatures, the internal molecular motion slows down and its viscosity significantly increases. At the glass transition temperature (T
g), the time needed for molecular rearrangement becomes comparable to the experimental time scale. At a lower cooling rate (q
+2 < q
+1) the supercooled liquid stays in metastable equilibrium until lower temperatures. Therefore, the glass transition is not a true thermodynamic phase transition depending on procedural variables such as cooling rate. As a consequence, there is not a single glassy state, and the properties of the glass depend upon how it was obtained [
1].
Clear evidence of the non-existence of a single glassy state is a slow, gradual approach of volume or enthalpy towards the extrapolated supercooled liquid equilibrium line that has been called “structural relaxation”. This process, associated with a slow molecular rearrangement, is experimentally observable in the glass transition range (see
Figure 1). It seems that structural relaxation is strongly affected by the supercooled liquid dynamics. An understanding of clues between long time-scale structural relaxation and short time-scale molecular dynamics of corresponding supercooled liquids is of fundamental importance for glass science.
On reheating of a glass, the structural relaxation peak is usually observed just above T
g. At higher temperatures the crystallization process takes place [
2]. These processes can be followed by thermal analysis methods such as differential thermal analysis (DTA) or differential scanning calorimetry (DSC). Both these methods are quite frequently used to study the structural relaxation and crystallization behavior in glasses. Usually, the kinetic parameters of such activation energies are extracted from experiments taken at different heating rates. In this paper, the physical meaning of these parameters determined for structural relaxation and crystallization of glassy selenium is analyzed and discussed with respect to the viscosity behavior of supercooled selenium.
3. Discussion
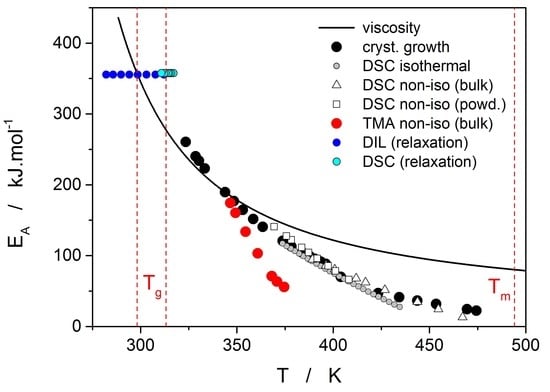
Thermo-kinetic data described in the previous section imply that the activation energy of most kinetic processes observable in glassy materials by thermal analysis varies with temperature. This gives an interesting opportunity to compare the apparent activation energies among the particular processes for the wide range of experimental conditions. In such a situation, the equilibrium viscosity can be seen as the overarching quantity offering the most sensible comparison for all other data. The activation energy of viscous flow E
η can be obtained from the tangent slope for the viscosity data depicted in
Figure 4:
The temperature dependence of E
η is shown in
Figure 10 (solid line).
Starting with the structural relaxation process, it is somewhat surprising that the activation energy of this process remains constant throughout the whole measured temperature range (9–45 °C). Note that structural relaxation is generally considered to be very closely interlinked with viscous flow. Nonetheless, the constant value of E
rel in the above-given temperature range was unambiguously confirmed from the dilatometric data [
3] (see, e.g.,
Figure 2), where E
rel was evaluated by non-linear optimization as well as by the linearization method [
23], and also from the calorimetric data [
3,
24] (see, e.g.,
Figure 3), where the non-linear optimization was complemented by the newly developed methodology [
25] based on the shift of the relaxation peak. Values of E
rel are shown in
Figure 10 for dilatometry (dark blue) and calorimetry (light blue). It is well apparent that the relaxation data exhibit a constant value of E
rel, not only in the glass transition temperature range commonly revealed via the non-isothermal measurement techniques (indicated by the red dashed lines), but also well below these temperatures. In the temperature window where the relaxation times considerably exceed the time-scale characteristic for the non-isothermal measurements, long-term isothermal annealing experiments need to be performed. Interestingly, the intersection of the E
rel and E
η well corresponds to the lowest value of T
g obtained during cooling within the commonly achievable time scale. The constancy of E
rel is a priori given by the definition of the TNM model, where the potential temperature-dependent component of E
rel is replaced by the T
f-based term on the right-hand side of Equation (4). Direct incorporation of the E
rel(T) dependence into Equation (4) might, however, be the way towards solving the occasionally raised questions [
26] associated with the universality of TNM formalism—as such it is certainly worth of further exploration.
The second process occurring during further heating of the glassy materials is crystal growth, observable either microscopically (see the crystal growth data in
Figure 4) or macroscopically, usually via calorimetric methods (see, e.g.,
Figure 5). Although the two approaches and the temperature ranges of their applicability differ to a great extent, the observed process is essentially the same and the corresponding activation energies should exhibit unified temperature dependence. In order to verify this hypothesis, E
G was determined from the crystal growth data depicted in
Figure 4 by using Equation (7) (via the direct tangential approach), and E
c was determined from both non-isothermal and isothermal DSC measurements by using the Kissinger (Equation (13)) and Friedman (Equation (14)) methods, respectively (see
Figure 7 for the two overall dependences). Again, the temperature-resolved tangential approach to the determination of E
c was adopted. The values of E
G and E
c are then compared in
Figure 10, showing a very good agreement and confirming the universal nature of the activation energy for the crystal growth process. The non-isothermal DSC crystallization measurements were performed (in addition to the bulk samples) also for a finely powdered glassy selenium. Despite the different crystallization mechanism occurring in case of the fine Se powders [
13,
14], the corresponding E
c(T) dependence also falls on the crystal growth master-curve depicted in
Figure 10, further confirming the universality of this aspect of the crystallization process kinetics.
With regard to the relation between the crystal growth rate and viscosity, it results from the Turnbull–Cohen formula where u is inversely proportional to η. However, it has been shown [
27] that for a number of materials the so-called decoupling of these two quantities occurs, breaking the Stokes–Einstein formalism [
28]. Formally, the decoupling is described by the apparent decoupling parameter ξ
a:
This rather empirical expression can be further corrected by accounting only for the rate at which the structural entities (atoms, molecules) present in the liquid phase are attached to the growth liquid-crystal interface. This correction is based on the elimination of the term f
p from the expression for the crystal growth rate u, where f
p is the probability of the structural entity, newly attached to the crystal growth interface, remaining within the crystalline phase:
ΔG
lc is the difference between the Gibbs energies of supercooled liquid and crystalline phases. Both forms of the decoupling parameter were essentially calculated from the ratio of the respective activation energies; ΔG
lc was calculated based on the standard thermodynamic expression [
29] from the selenium enthalpy and entropy of fusion and the heat capacity data published in [
30].
Temperature dependences of both forms of the decoupling parameter are shown in
Figure 11. Values of ξ
a and ξ indicate that at low temperatures/growth rates almost no decoupling between u and η can be found (in fact, slight negative decoupling occurs below 340 K). However, as the temperature increases the decoupling becomes more prominent and very well recognizable at temperatures above 370 K. Increasing temperature also results in a rising difference between the two forms of decoupling parameters ξ and ξ
a. This difference is negligible up to ~365 K but then rapidly increases with the exponential increase of the correction term f
p. Note that the melting entropy of crystalline selenium is ΔS
m ≈ 1.5R [
10]. Such a relatively small value in combination with low supercooling causes relatively large difference between ξ and ξ
a at higher temperatures. A similar effect may also bring N-type heat capacity of supercooled selenium [
30], which effectively lowers the f
p contribution. Interestingly, both decoupling dependences exhibit a sudden step-like decrease of the decoupling parameter at 400 K. This is the consequence of the change in preferential morphology of the growing crystallites (transition from spherulitic form B to spherulitic form A, as described in [
9]). The step-like change very well agrees with the break on the temperature dependences of the corresponding integral data utilized for calculation of E
G and E
c, as depicted in
Figure 11, where the dashed vertical line indicates the break point. It is noteworthy that the corrected rate of growth u
kin for the high-temperature spherulitic form A does not show further increase in decoupling (which would be represented by the decrease of ξ) and is close to ξ = 0.62.
The last data set depicted in
Figure 10 is the one corresponding to the TMA crystallization measurements. Evaluation of activation energy from the TMA data was done similarly as in the case of non-isothermal DSC, i.e., by the tangential approach of the Kissinger dependence (Equation (13)), where the extrapolated endset T
e (see
Figure 9) was used as the characteristic temperature. It was shown for several other chalcogenide glassy systems [
31,
32] that the activation energy evaluated in this way from the TMA measurements is in a good agreement with E
c from DSC, but the data are (due to the choice of the extrapolated characteristic temperature) shifted to lower temperatures; that is, the crystal growth process is seemingly observed “in advance” and the E
A–T dependence gets shifted to lower temperatures. From this point of view, it is the high-temperature points shown in
Figure 10 that in this dependence represent the commonly observed behavior. Contrary to what was observed for most other studied chalcogenides, E
A rapidly increases at lower temperatures. The exact position of T
e depends on many factors (including applied force, sample geometry, nucleation density, location and morphology of forming crystallites, etc.) but essentially can be understood as the competition between the viscous flow and crystal growth rate (which also depends on viscosity). In case of amorphous selenium, the position of T
e appears to be driven more by viscous flow (in combination with surface tension) at low temperatures. Thus, the activation energy determined from the TMA measurements at low q
+ gets closer to E
η.
There are of course many consequences associated with the temperature variation of crystallization activation energies. In the last part of the Discussion section we will focus on the model-based master-plot evaluation method utilizing the characteristic kinetic functions z(α) and y(α). The former can be expressed as the product f(α)·g(α), see Equation (11), and as such is invariable with E
A. On the other hand, function y(α) is proportional to f(α), which utilizes E
A during the transformation of experimental data, see Equation (15). It naturally suggests itself to use the full E
c(T) dependence (see
Figure 10) in Equation (15). However, the y(α) function is too sensitive to the value of activation energy, and the large variation of E
c throughout each non-isothermal DSC measurement effectively results in y(α) distortions reminiscent of output obtained for the JMA formalism with the sub-unity kinetic exponent m. It is therefore reasonable to replace the full E
c(T) dependence by constant values of E
c, selected for each measurement individually based on the arbitrarily determined characteristic temperature point. If the value of E
c for the temperature corresponding to the maximum transformation rate (maximum of the DSC peak) is used, the resulting values of JMA kinetic exponents are too large to be physically meaningful. Nevertheless, if we consider that the dimensionality of the formed crystallites is being already set at the start of the crystallization process, and, correspondingly, we utilize E
c values corresponding to α = 0.10, the data depicted in
Figure 12 are obtained.
As can be seen, most datapoints can be reasonably described by using the JMA kinetic exponent m = 3, which may correspond to the assumption that for bulk selenium samples the crystal growth starts dominantly via formation of three-dimensional volume-located crystallites.
4. Materials and Methods
Glassy selenium was prepared from pure elements (5N, Sigma-Aldrich, Prague, Czech Republic) by melt-quenching. Elementary Se was melted in an evacuated fused silica ampoule, which was then let to cool in air. The glassy material was crushed in agate mortar and sieved through defined mesh so that the various particle size fractions were obtained. Powder DSC crystallization data reported in this paper were obtained for the 20–50 µm fraction [
13,
14]. Pieces of glass with a diameter larger than 1 mm were used for the DSC relaxation and bulk crystallization measurements [
3,
13]. Melt-quench in thin ampoules was utilized to prepare cylindrical Se samples. The ampoules were quenched vertically to obtain a glassy ingot, which was then sawed into samples with the following diameters (d
m) and heights (h
m): For viscosity measurements d
m = 6 mm and h
m = 2.5 mm [
12], for microscopic crystal growth measurements d
m = 4 mm and h
m = 2 mm [
10] and for TMA crystallization measurements d
m = 4 mm and h
m = 1 mm.
Experimental setups and details of most measurements were already published in the respective papers: Structural relaxation by DSC and dilatometry in [
3,
24], viscosity in [
12], microscopic crystal growth in [
10] and non-isothermal powder and bulk crystallization by DSC in [
13,
14]. The new, previously unpublished data are those for isothermal bulk crystallization measured by DSC and non-isothermal crystallization measured by TMA.
The isothermal DSC data were obtained using a Q2000 DSC (TA Instruments, Prague, Czech Republic) equipped with a cooling accessory, autolid, autosampler and T-zero Technology. Dry nitrogen was used as the purge gas at a rate of 50 cm
3·min
−1. The calorimeter was calibrated using In, Zn and H
2O. The stability of the DSC signal was checked daily. Open T-zero low-mass pans were used. Regarding the applied temperature program, the sample (8–10 mg) was first subjected to a 5 min isotherm at 45 °C and then heated at 100 °C·min
−1 to a selected temperature
Ti, where the sample was allowed to isothermally crystallize until the crystallization process was complete. The isothermal crystallization temperatures utilized in the case of each particle size fraction were 100, 105, 110, 115, 120, 125, 130, 135, 140, 145, 150, 155 and 160 °C. In order to obtain a baseline for the isothermal measurement, each DSC pan with a crystalline sample of glass was kept in the DSC cell and the above-described temperature procedure was repeated (in this way the data subtracted from the isothermal crystallization signal truly surrogated the presence of an inert material with similar heat capacity, mass, grain size and positioning in the DSC pan/cell). Perfect flatness of the baseline and reproducibility of the crystallization measurements were confirmed. For the extensive testing of the suitability and repeatability of the initial 100 °C·min
−1 heating ramp, see [
15].
The thermomechanical measurements were realized by using a TMA Q400EM (TA Instruments), where the cylindrical samples were compressed in-between two alumina plates, and the force applied to the sample was 30 mN. A linear heating rate was applied to study the effect of crystal growth suppressing the decrease of sample height caused by viscous flow. The following heating rates were applied between 35 and 170 °C: 0.2, 0.5, 1, 2, 3, 4 and 5 °C·min−1.