Measurement of Circular Dichroism Spectra without Control of a Phase Modulator using Retardation Domain Analysis
Abstract
:1. Introduction
2. Results and Discussion
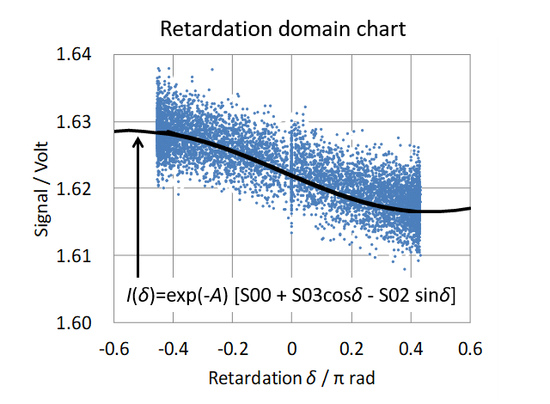
2.1. Circular Dichroism (CD) Measurement with Various Phase Modulator Settings
2.2. Measurement of CD Spectra
2.3. Measurement of Linear Dichroism (LD) Spectra
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

References
- Johnson, W.C., Jr. Circular dichroism instrumentation. In Circular Dichroism and the Conformational Analysis of Biomolecules, 1st ed.; Fasman, G.D., Ed.; Plenum: New York, NY, USA, 1996; pp. 635–652. ISBN 0-306-45142-5. [Google Scholar]
- Shindo, Y.; Nakagawa, M. Circular dichroism measurements. I. Calibration of a circular dichroism spectrometer. Rev. Sci. Instrm. 1985, 56, 32–39. [Google Scholar] [CrossRef]
- Shindo, Y. Application of polarized modulation technique in polymer science. Polym. Sci. 1995, 34, 3369–3384. [Google Scholar] [CrossRef]
- Satozono, H. Elimination of artifacts derived from the residual birefringence of a phase modulator for circular dichroism by retardation domain analysis. Opt. Lett. 2015, 40, 1161–1164. [Google Scholar] [CrossRef]
- Takakuwa, T.; Konno, T.; Meguro, H. A new standard substance for calibration of circular dichroism: Ammonium d-10-camphorsulfonate. Anal. Sci. 1985, 1, 215–218. [Google Scholar] [CrossRef]
- Nafie, L.A. Dual polarization modulation: A real-time, spectral-multiplex separation of circular dichroism from linear birefringence spectral intensities. Appl. Spectrosc. 2000, 54, 1634–1645. [Google Scholar] [CrossRef]
- Kuroda, R.; Harada, T.; Shindo, Y. A solid-state dedicated circular dichroism spectrophotometer: Development and application. Rev. Sci. Instrm. 2001, 72, 3802–3810. [Google Scholar] [CrossRef]
- Provenzano, C.; Pagliusi, P.; Mazzulla, A.; Cipparrone, G. Method for artifact-free circular dichroism measurements based on polarization grating. Opt. Lett. 2010, 35, 1822–1824. [Google Scholar] [CrossRef] [PubMed]
- Arteaga, O.; Freudenthal, B. Mueller matrix polarimetry with four photoelastic modulators: Theory and calibration. Appl. Opt. 2012, 51, 6805–6817. [Google Scholar] [CrossRef] [PubMed]
- Go, N. Optical activity of anisotropic solutions. II. J. Phys. Soc. Jap. 1967, 23, 88–97. [Google Scholar] [CrossRef]
- Jensen, H.P.; Schellman, J.A.; Troxell, T. Modulation techniques in polarization spectroscopy. Appl. Spectrosc. 1978, 32, 192–200. [Google Scholar] [CrossRef]
- Arteaga, O. Historical revision of the differential Stokes – Mueller formalism: Discussion. J. Opt. Soc. Am. A. 2017, 34, 410–414. [Google Scholar] [CrossRef] [PubMed]
- Norden, B.; Rodger, A.; Dafforn, T. Linear Dichroism and Circular Dichroism; RSC Publishing: Cambridge, UK, 2010; p. 34. ISBN 978-1-84755-902-9. [Google Scholar]



| 254 nm | 320 nm | |
|---|---|---|
| S00 | 1.62 | 1.63 |
| S02 | 5.95 × 10−3 | 5.80 × 10−3 |
| S03 | −2.39 × 10−4 | 0.67 × 10−4 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Satozono, H. Measurement of Circular Dichroism Spectra without Control of a Phase Modulator using Retardation Domain Analysis. Molecules 2019, 24, 1418. https://doi.org/10.3390/molecules24071418
Satozono H. Measurement of Circular Dichroism Spectra without Control of a Phase Modulator using Retardation Domain Analysis. Molecules. 2019; 24(7):1418. https://doi.org/10.3390/molecules24071418
Chicago/Turabian StyleSatozono, Hiroshi. 2019. "Measurement of Circular Dichroism Spectra without Control of a Phase Modulator using Retardation Domain Analysis" Molecules 24, no. 7: 1418. https://doi.org/10.3390/molecules24071418
APA StyleSatozono, H. (2019). Measurement of Circular Dichroism Spectra without Control of a Phase Modulator using Retardation Domain Analysis. Molecules, 24(7), 1418. https://doi.org/10.3390/molecules24071418