Next Article in Journal
Adlay Testa (Coix lachryma-jobi L. var. Ma-yuen Stapf.) Ethanolic Extract and Its Active Components Exert Anti-Proliferative Effects on Endometrial Cancer Cells via Cell Cycle Arrest
Next Article in Special Issue
Surface Modification Effect and Electrochemical Performance of LiOH-High Surface Activated Carbon as a Cathode Material in EDLC
Previous Article in Journal
L-Glutaminase Synthesis by Marine Halomonas meridiana Isolated from the Red Sea and Its Efficiency against Colorectal Cancer Cell Lines
Previous Article in Special Issue
Role of Zinc-Doped Bioactive Glass Encapsulated with Microspherical Gelatin in Localized Supplementation for Tissue Regeneration: A Contemporary Review
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 26
Issue 7
10.3390/molecules26071965
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Guanidine–Amide-Catalyzed Aza-Henry Reaction of Isatin-Derived Ketimines: Origin of Selectivity and New Catalyst Design

by
Jiajia He
1,
Dianyong Tang
2,
Changwei Hu
1 and
Zhishan Su
1,*
1
Key Laboratory of Green Chemistry and Technology, Ministry of Education, College of Chemistry, Sichuan University, Chengdu 610064, China
2
College of Pharmacy & International Academy of Targeted Therapeutics and Innovation, Chongqing University of Arts and Sciences, Chongqing 402160, China
*
Author to whom correspondence should be addressed.
Molecules 2021, 26(7), 1965; https://doi.org/10.3390/molecules26071965
Submission received: 24 February 2021 / Revised: 29 March 2021 / Accepted: 29 March 2021 / Published: 31 March 2021
(This article belongs to the Special Issue Multi-functional Materials and Applications—Special Issue for ICMMA2020)
Browse Figures
Versions Notes

Abstract

:
Density functional theory (DFT) calculations were performed to investigate the mechanism and the enantioselectivity of the aza-Henry reaction of isatin-derived ketimine catalyzed by chiral guanidine–amide catalysts at the M06-2X-D3/6-311+G(d,p)//M06-2X-D3/6-31G(d,p) (toluene, SMD) theoretical level. The catalytic reaction occurred via a three-step mechanism: (i) the deprotonation of nitromethane by a chiral guanidine–amide catalyst; (ii) formation of C–C bonds; (iii) H-transfer from guanidine to ketimine, accompanied with the regeneration of the catalyst. A dual activation model was proposed, in which the protonated guanidine activated the nitronate, and the amide moiety simultaneously interacted with the ketimine substrate by intermolecular hydrogen bonding. The repulsion of CPh3 group in guanidine as well as N-Boc group in ketimine raised the Pauli repulsion energy (∆EPauli) and the strain energy (∆Estrain) of reacting species in the unfavorable si-face pathway, contributing to a high level of stereoselectivity. A new catalyst with cyclopropenimine and 1,2-diphenylethylcarbamoyl as well as sulfonamide substituent was designed. The strong basicity of cyclopropenimine moiety accelerated the activation of CH3NO2 by decreasing the energy barrier in the deprotonation step. The repulsion between the N-Boc group in ketimine and cyclohexyl group as well as chiral backbone in the new catalyst raised the energy barrier in C–C bond formation along the si-face attack pathway, leading to the formation of R-configuration product. A possible synthetic route for the new catalyst is also suggested.

Graphical Abstract

1. Introduction

The aza-Henry reaction (or nitro-Mannich reaction) is one of the most effective methods for the construction of carbon–carbon bonds with concomitant generation of two vicinal stereogenic centers bearing nitro and amino functional groups [1]. The resulting β-nitroamine products can be conveniently converted into a variety of chiral building blocks (e.g., α-amino acids [2,3,4,5,6] and 1,2-diamines [7,8,9,10]); therefore, the development of efficient procedures to promote the reaction in a highly enantioselective way have received wide attention. Since the first example of a catalytic enantioselective aza-Henry reaction was reported by Shibasaki [11], many metal-based [12,13,14,15] and organic catalysts [16,17] have been employed in the nucleophilic addition of aldimine, affording β-nitroamines in high yield and stereoselectivity [18]. Compared to aldimine substrate, the reports using a ketimine as the electrophile in the asymmetric Henry reaction were limited, due to its low reactivity and poor prochiral face control [19].
The aza-Henry reaction of isatin-derived N-Boc ketimine could produce 3-substituted-3-amino-2-oxindoles, which are key structural units in many natural products and pharmacologically active molecules [20,21,22,23]. The bis(imidazolidine) pyridine-NiCl2 [24], bis-oxazoline-Cu(II) [25] and N,N′-dioxide-Cu(I) [26] complexes were proven to be efficient organometallic catalysts for aza-Henry reaction of isatin-derived ketimines under mild conditions. In organocatalysis, the cinchona alkaloid and its derivatives are popular catalysts for the construction of indole skeletons [27]. A dual activation model is generally adopted to explain catalyst–ketimine interactions as well as the stereoinduction of catalysts [28], in which the tertiary amine group and a hydrogen-bond donor group orientated on the chiral scaffold activate CH3NO2 and govern facial selectivity in the reaction simultaneously. For example, Chimni et al. proposed that the OH group at C6′-position of the cinchona alkaloid affected the reactivity and selectivity of the product. In the catalysis, the isatin ketimine bonded to the C6′–OH group of the catalyst by hydrogen bonding. Meanwhile, the quinuclidine tertiary amine moiety deprotonated the nitromethane and induced the formed nitronate to attack the ketimine from the re-prochiral face [29]. Chiral thiourea [30] and thiourea- [31] or sulphone-amide-modified cinchona derivatives [32] are also applied into aza-Henry reactions of ketimine. They serve to simultaneously activate the electrophile and nucleophile during C–C bond formation by hydrogen bonding, and are essential for reaction rate and selectivity. Dixon and co-workers designed a bifunctional iminophosphorane organocatalysts to enhance the synergistic effects of Brønsted base and H-bond-donor in the addition of nitromethane to unreactive ketimine [33]. Chen and co-workers theoretically studied the mechanism of quinine derivative-catalyzed aza-Henry reaction of isatin-derived ketimine using the density functional theory (DFT) method. The synergistic effects of multiple non-covalent interactions (i.e., classical, and non-classical H bonds and anion–π interactions) were responsible for the high reactivity and enantioselectivity of reactions [34]. In addition, chiral phase transfer catalysts with a quaternary ammonium center derived from l-tert Leucine also exhibited good catalytic performance in the aza-Henry reaction of isatin-derived ketimines. The urea motif captured the isatin-derived ketimines by H-bond interactions. Meanwhile, the nucleophilic nitro group anion paired with ammonium motifs by electrostatic interactions [35].
Due to strong basicity and hydrogen-bond donor ability, chiral guanidine organocatalysts have been widely used in many asymmetric catalysis (e.g., Michael reaction [33], Henry reaction [36], and Mannich reaction [37]). It can abstract a proton from the substrate and catalyze the reaction as its conjugated acid (i.e., the guanidinium cation). A bifunctional Brønsted acid activation mode has been proposed, in which the electrophile and nucleophile are positioned by a guanidinium cation via hydrogen bonding [38,39,40,41,42,43]. In 2015, Feng and Liu [44] developed an open-chain guanidine–amide organocatalyst for asymmetric aza-Henry reactions of isatin-derived N-Boc ketimines. The 3-substituted 3-amino-2-oxindoles were obtained with excellent results (up to 99% yield, 94% ee). They proposed that the guanidine moiety deprotonated the nitromethane and bonded the nucleophile through dual hydrogen-bonds. The amide unit acted as a Brønsted acid to activate the ketimine substrate simultaneously. The shielding effect from phenyl groups of the amide unit induced the nucleophile to preferably attack the ketimine from the re-face, affording an R-configuration product.
Herein, we performed a theoretical investigation on the mechanisms and stereoselectivity of asymmetric aza-Henry reactions between isatin-derived N-Boc ketimines and nitroalkane (see Scheme 1). Based on the calculations, we modified the structure of guanidine–amide and design a new catalyst containing cyclopropenimine and 1,2-diphenylethylcarbamoyl as well as 2,6-difluorobenzenesulfonamide group to enhance its catalytic activity and chiral induction ability. Our hope was that through the synergistic effects of the stronger Brønsted base and the hydrogen bonding donor as well as the modification of the chiral backbone, superior reactivity and selectivity could be obtained. These results are expected to provide useful information for the synthesis of new chiral organocatalysts for aza-Henry reactions of ketimine.

2. Results and Discussion

2.1. Analysis of Reactivity at N Atoms in G1

It is well known that guanidine can act as a Brønsted base to activate the reactant by hydrogen bonding in organocatalysis [45,46,47,48]. Three types of nitrogen atoms (N2, N3 and N5) exist in the structural unit of guanidine moiety; therefore, we first optimized the geometry of G1 and evaluated the reactivity of nitrogen atoms. As shown in Table S1, Supplementary Materials, the key structural parameters in G1 were similar to those of the corresponding crystal structure obtained in the experiment [44]. Intramolecular hydrogen bonding exists between the guanidine moiety and amide moiety, with an N2⋯H10 distance of 1.94 Å. The proton affinity of the N2 atom (226.4 kcal·mol−1) is higher than those of N3 (196.3 kcal·mol−1) and N5 (199.6 kcal·mol−1). This indicated that the N2 atom with strong basicity [38,39,40,41,42,43,49] could work as the reacting site for the deprotonation of CH3NO2 in the Henry reaction.

2.2. Catalytic Mechanism for R1a

As shown in Scheme 2, the reaction mechanism of asymmetric Henry reactions between ketimine (R1a) and nitromethane (R2) consisted of three consecutive steps, including: (i) the deprotonation of CH3NO2 by guanidine–amide catalyst; (ii) formation of a C–C bond; and (iii) H-transfer from the guanidine to ketimine substrate, accompanied with the regeneration of the catalyst. The step associated with the activation of CH3NO2 was predicted to be the rate-determining step (RDS) [18]. The C–C bond formation step was the chiral-controlling step, affording R- or S-enantiomers along re- or si-face attack pathways, alternatively.

2.2.1. Activation of CH3NO2

When G1 interacted with CH3NO2, it underwent a change of conformation, constructing O8⋯H4 intramolecular hydrogen bonding. This new conformation facilitated the N2 atom and amide moiety to interact with CH3NO2 simultaneously by intermolecular hydrogen bonding [50]. For the molecular complex G1-COM, the N2⋯H16 and H10⋯O18 distances were 2.27 Å and 2.24 Å, respectively. AIM analysis indicated that the electronic densities (ρ) at the (3, −1) bond critical points (BCP) (a and b in Figure 1) were 0.017 a.u. and 0.014 a.u., with the corresponding hydrogen bonding energies of Ea = −2.99 kcal·mol−1 and Eb = −2.27 kcal·mol−1, respectively [51]. Compared to the free CH3NO2, the C15–H16 bond in G1-COM enlengthened from 1.09 to 1.10 Å. Meanwhile, the corresponding Wiberg bond index was decreased from 0.921 to 0.875. These results suggested that the C–H bond in CH3NO2 was significantly weakened. The deprotonation of CH3NO2 occurred via transition state G1-TS1, accompanied with the global electron density transfer (GEDT) of 0.23 e from G1 to CH3NO2. Accordingly, an ion-pair intermediate (G1-IM1) was formed. This step was endergonic by 3.3 kcal·mol−1, with an energy barrier of 10.6 kcal·mol−1.

2.2.2. Formation of C–C Bond

Starting from G1-IM1, four molecular complexes (G1-I-re-IM2 ~ G1-II-si-IM2) were formed in models I and II, according to the different orientations of N-Boc ketimine (R1a) and nitronate (Scheme 3). The hydrogen bonding between the protonated guanidine with R1a and nitronate were verified by AIM analysis because the magnitudes of Laplacian of electron densities (∇2ρ) at (3, −1) bond critical points (a and b) were positive (Figure S1). Electrostatic potential (ESP) analysis (Figure 2b) for the protonated guanidium fragment in G1-IM1 indicated that the surface global maximum (121.2 kcal·mol−1) was from the positively charged H16 atom (not H10 atom in Figure 2a), leading to preferable orientation of the CH2NO2 anion by the H16 atom in the guanidium cation [52]. Accordingly, G1-I-re-IM2 and G1-I-si-IM2 in model I were slightly more stable than those of G1-II-re-IM2 and G1-II-si-IM2 by 0.9~1.7 kcal·mol−1 (Figure 3). In the following step, the C=N bond addition was achieved by nucleophilic attack of the nitronate towards the C13 atom of R1a along four pathways (I-re, I-si, II-re or II-si), followed by easy proton transfer from the N2 atom to N14 atom. The hydrogen bonds between the guanidine cation and N-Boc ketimine (R1a) in four TSs were also proved by AIM analysis (Figure S2). The relative Gibbs free energy of transition states G1-I-re-TS2 and G1-I-si-TS2 were 1.1 and 2.3 kcal·mol−1, respectively, which were lower than those of G1-II-re-TS2 and G1-II-si-TS2 (2.4 and 4.0 kcal·mol−1, respectively; Figure 3 and Figure 4). In addition, the activation barrier in the C–C bond formation step along the I-re path (∆G≠ = 2.4 kcal·mol−1) was lower than that of the I-si path (∆G≠ = 4.6 kcal·mol−1) by 2.2 kcal·mol−1. For the II-re pathway, ∆G≠ in the C–C bond formation step was 0.4 kcal·mol−1 higher than that along I-re. Meanwhile, both G1-II-re-IM2 and G1-II-re-TS2 were less stable than the corresponding species in I-re pathway. These results indicated that the predominant R-configuration product observed in the experiment was predominantly produced along the I-re path. According to the Curtin–Hammett principle [53], the theoretical enantioselectivity (ee %) was 85%, which was close to the experimental result (91% ee).
We further analyzed the orbital interactions between N-Boc ketimine (R1a) and nitromethane in the C–C bond formation step. The structures of G1-I-re-TS2 and G1-I-si-TS2 were decomposed into a guanidine–nitromethane ion-pair fragment (G1-R2, Frag. 1) and an N-Boc ketimine fragment (R1a, Frag. 2). The schematic orbital interaction diagrams are shown in Figures S3 and S4. For the highest occupied molecular orbital (HOMO) of G1-I-re-TS2, it was mainly formed by the mixture of the occupied highest occupied fragment orbital (HOFO) of the G1-R2 fragment (Frag. 1, 73.35%) and the unoccupied lowest unoccupied fragment orbital (LUFO) of the R1a fragment (Frag. 2, 16.99%). The electronic density delocalization between BD(π) C15–N17 to the unoccupied BD(π*) C13–N14 (E(2) = 19.2 kcal·mol−1) promoted the formation of a C13–C15 bond, contributing to the orbital interaction energy (∆Eorb) of −45.29 kcal·mol−1. Similar molecular orbital interactions was also observed in G1-I-si-TS2, with less contribution of the HOFO orbital of the G1-R2 fragment (63.59%) in the HOMO.
For comparison, we also studied the dual hydrogen bond model proposed by the experiment [44]. Four optimized geometries of transition states (G1-I-re-TS2-a ~ G1-II-si-TS2-a) along re- and si-pathways in two models were located at the same theriacal level (Figure S5). The ∆G of transition states in model I were significantly lower than those in model II by 7.2~10.2 kcal·mol−1. For the TSs in model I, the CH2NO2 anion was positioned by two NH groups in the guanidine moiety of G1 catalyst, with a N–H⋯O distance of 1.95~2.47 Å. It seemed that two Cy groups in the guanidine exerted comparable hindrance effects towards ketimine in the two competing transition states. Moreover, the ∆G of G1-I-re-TS2-a was 0.9 kcal·mol−1 less stable than that of G1-I-si-TS2-a, affording the S-product as a major one (not the R-product observed in experimental observation). Although the relative Gibbs free energy of G1-I-re-TS2-a in C–C bond formation steps were lower than that of G1-I-re-TS2 by 2.6 kcal·mol−1, the guanidine–amide catalyst had to undergo remarkable conformation changes from G1-IM1 to realize the pre-organized structure in TSs (as shown in Figure S6, the ∆G≠ to change the orientation of two N–Cy groups in the guanidine cation were about 10~13 kcal·mol−1). Thus, unless specified, we just focus on the conformation of the guanidine cation with an intramolecular H4⋯O8 in the following discussions.

2.2.3. Origin of Stereoselectivity

To understand the origin of stereoselectivity in the aza-Henry reaction between ketimine (R1a) and nitromethane (R2) catalyzed by guanidine G1, we analyzed the structures of the two key transition states (i.e., G1-I-re-TS2 and G1-I-si-TS2) in the chiral-controlling step (i.e., C–C bond formation step). As shown in Figure 4, the N-Boc group was placed at the same side as the bulky CPh3 group of G1 in the G1-I-si-TS2, with a distance of about 2.83 Å. The steric repulsion between them increased the Pauli repulsion energy ∆Epauli (67.8 vs. 83.5 kcal·mol−1), as well as the strain energy ∆Estrain of the two reacting fragments (9.8 vs. 12.9 kcal·mol−1) at TSs along the I-si pathway (Figure 5). As a result, the activation energy barrier (∆G≠) along the I-si pathway was higher than those along the I-re pathway by 2.2 kcal·mol−1. In contrast, the unfavorable steric repulsion could be efficiently avoided in G1-I-re-TS2 because the CPh3 group was far away from the N-Boc group. The stronger interaction between the deformed reactants played the crucial factor in favoring the re-pathway [54,55]. That is, the more stabilizing electrostatic energy (∆Velstat) and orbital energy (∆Eorb) efficiently offset the Pauli repulsion of two reacting fragments. Moreover, the Bn group with structural flexibility could weaken the steric hindrance from the CPh3 group, contributing to the low relative Gibbs free energy of transition state G1-I-re-TS2 (1.1 vs. 2.4 kcal·mol−1 for G1-I-si-TS2). The noncovalent interaction (NCI) plots in Figure S7, Supplementary Materials, also reveal a large green region in G1-I-re-TS2, associated with the stabilizing CH2⋯π interaction between the Bn group in ketimine and CPh3 group in the catalyst.
When the ketimine R1b with a small N-COOEt group was used as a reactant in the catalytic aza-Henry reaction, the repulsion between the N-protected group in R1b and CPh3 group in G1 was significantly decreased. Accordingly, the ∆∆G of the two competing transition states (G1-1b-I-re and G1-1b-I-si in Figure 6 and Figure S8) was decreased to 0.4 kcal·mol−1, leading to low stereoselectivity. The inferior enantioselectivity for R1b was also observed in the experiment [44]. In contrast to R1a, the charge accumulated on the O12 atom in R1b was slightly low (−0.580 e vs. −0.584 e in R1a). In addition, the H16⋯O12 distances in G1-1b-I-re-IM2 and G1-1b-I-si-IM2 were 1.976 and 1.986 Å, respectively, which were longer than those in the corresponding intermediates for R1a (1.950 and 1.917 Å). Due to weak catalyst–R1b interactions, more energy was required to deform R1b to the TS geometries. Accordingly, the ΔE≠strain values of G1-1b-I-re-TS2 and G1-1b-I-si-TS2 (11.3 and 12.7 kcal·mol−1) were more destabilizing than that of G1-I-re-TS2 (9.8 kcal·mol−1), leading to higher activation barriers.
We then removed a phenyl in G1 to obtained guanidine–amide catalyst G2. The optimized geometries of the two key transition states (i.e., G2-1a-I-re-TS2 and G2-1a-I-si-TS2) in the C–C bond formation step were shown in Figure 7 and energy profile was in Figure S9, Supplementary Materials. Similar to G1, the re-face attack pathway was still more favorable than the si-face attack pathway in model I. However, the ∆∆G of the two competing transition states (G2-1a-I-re-TS2 and G2-1a-I-si-TS2) was decreased to 0.8 kcal·mol−1, associated with low selectivity (ee = 68%). Thus, the bulky CPh3 substituent was the key structural unit for asymmetric induction in the chiral guanidine–amide catalyst G1. The steric repulsion between N-Boc ketimine and CPh3 substituent in G1 increased the Pauli repulsion as well as the strain energy of the reacting fragments in the chiral-controlling step, contributing to the excellent stereochemical outcomes in the asymmetric aza-Henry reaction of N-Boc ketimine.

2.2.4. Turnover Frequency (TOF) Analysis

To evaluate the efficiency of the catalyst G1 along four pathways in Figure 3, the theoretical turnover frequency (TOF) of the catalytic cycle was calculated [56]. As shown in Table 1, G1-1a-I-re-IM2 ~ G1-1a-II-si-IM2 were predicated to be TOF-determining intermediates, and G1-1a-I-re-TS2 ~ G1-1a-II-si-TS2 were the TOF-determining transition states. The TOF value along the re-face pathway in model I was 2.06 × 1010 s−1, which was higher than those of other three pathways. That is, G1 exhibited better catalytic efficiency when the Henry reaction of N-Boc ketimine R1a occurred along the I-re-pathway.
Based on the results above, a working model was proposed to explain the activation of the reactants as well as the chiral induction effect of the guanidine–amide catalyst in asymmetric aza-Henry reactions. As shown in Figure 8, three factors were important for the high level of stereoselective outcomes in the catalysis, including: (i) intramolecular hydrogen bonding between the amide skeleton and imine unit of guanidine enhanced the stability of catalyst, and fixed the position of the bulky CPh3 group in the chiral environment; (ii) N-Boc in the ketimine was placed away from the CPh3 group, avoiding the unfavorable steric repulsion from the CPh3 group; and (iii) the nitronate was oriented by hydrogen bonding from the imine moiety of guanidine for the favorable re-face attack for predominant R-configuration products.

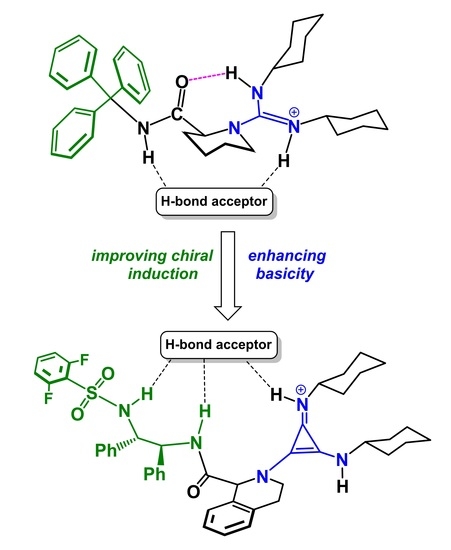
2.3. Design of New Catalysts

In 2012, Lambert et al. developed a chiral 2,3-bis(dialkylamino) cyclopropenimine for the Michael reaction of a glycine imine substrate. The strong basicity of the cyclopropenimine moiety accelerated the deprotonation of glycine imine. In addition, the alcohol moiety of the catalyst activated methyl acrylate via H-bonding, contributing to the high enantioselectivity results [57]. Feng and Liu found that the modified guanidine–amide with 1,2-diphenylethylcarbamoyl and the 2,6-difluorobenzenesulfonamide group was efficient in the asymmetric catalysis [58]. Inspired by the excellent performance of cyclopropenimine in Brønsted base catalysis, we modified the structure of G1 by replacing the guanidine moiety with cyclopropenimine. In addition, the diamine with a 2,6-difluorob-enzenesulfonamide group was introduced into the molecular skeleton of the catalyst. Two new catalysts (G3 and G4) were designed (Scheme 4), and the corresponding optimized structures are shown in Figure 9. The mechanism of aza-Henry reaction between N-Boc ketimine (R1a) and CH3NO2 catalyzed by G3 and G4 in low-energy model I were studied at the same theoretical level to evaluate their catalytic performance as well as chiral induction effect.
The calculations indicated that the reaction mechanisms in the presence of G3 or G4 were the same as that of G1. Due to the strong basicity of cyclopropenimine moiety, the energy barriers associated with the activation of CH3NO2 were decreased to 7.9 kcal·mol−1 for G3, and 7.2 kcal·mol−1 for G4. When protonated G3 interacted with N-Boc ketimine R1a, the molecular complexes G3-re-IM2 and G3-si-IM2 were formed, in which the amide moiety activated ketimine by hydrogen bonding. Compared to G3-si-IM2, the N-Boc in G3-re-IM2 was closer to the six-membered ring of the chiral skeleton as well as the CPh3 group, with a distance of about 2.51 Å and 2.46 Å, respectively. Suffering from the steric repulsion from the catalyst, the relative Gibbs free energy of transition state G3-re-TS2 in the C–C bond formation along the re-face attack pathway was slightly higher than via the transition state G3-si-TS2 by 0.3 kcal·mol−1 (Figure 10). Consequently, the product with S-configuration was formed with slight predominance.
When G4 was used as the catalyst, the O9⋯H13 and N3⋯H11 intramolecular hydrogen bonding weakened its structural flexibility (Figure 9). The molecular complexes G4-re-IM2 and G4-si-IM2 were formed, in which the cyclopropenimine activated the CH2NO2 anion, and N10-H11 as well as the N12-H13 moiety interacted with ketimine R1a by double hydrogen-bonding. In the following step, the C–C bond was constructed via transition state G4-re-TS2 or G4-si-TS2, alternatively (Figure 11 and Figure 12). Compared to G4-re-TS2, the N-Boc group of ketimine in G4-si-TS2 was closer to 2,6-difluorobenzenesulfonamide, Ph group in the chiral backbone, as well as Cy group in the guanidine moiety. This unfavorable steric hindrance made G4-si-TS2 less stable than G4-re-TS2 by 6.3 kcal·mol−1. The activation barrier from G4-si-IM2 to G4-si-IM3 along the si-pathway was 3.1 kcal·mol−1, which was higher than ΔG≠ from G4-re-IM2 to G4-re-IM3 along the re-pathway (1.9 kcal·mol−1), contributing to the predominant formation of P-R (inconsistent with G1). In addition, because G4-re-IM2 was 5.1 kcal·mol−1 lower than that of G4-si-IM2, the catalyst concentration could be higher in the G4-re-IM2 reaction system.
Therefore, the synergistic effects of the stronger Brønsted base (i.e., cyclopropenimine) and dual hydrogen bonding donor accelerated the activation of CH3NO2 and governed the facial selectivity in substrate binding, contributing to good reactivity and selectivity.
According to synthesis investigation on guanidine derivatives with 1,2-diphenylethane-1,2-diamine groups by Feng and Liu [59], and guanidine–cyclopropenimine proton sponges by Dudding [58], we proposed a possible synthesis route for a new catalyst, G4 (Scheme 5). We expected that these results would be helpful for the development for the new catalytic system in the aza-Henry reaction of ketimine.

3. Materials and Methods

All DFT calculations were performed with the Gaussian 09 program [60]. The structures were optimized using the M06-2X [61] -D3 [62] function with 6-31G(d,p) basis set, and characterized by the vibrational frequency analysis at 243 K. The SMD solvation model [63] for toluene was employed in the structure optimization. The intrinsic reaction coordinate (IRC) [64] paths were traced to check the energy profiles connecting each transition state to the associated minima of the proposed mechanism. Single point energy was obtained using the same functional and 6-311+G(d,p) basis set. Natural bond orbital (NBO) [65] and reactivity indices (electrophilicity index ω and nucleophilicity index N) analysis for the reactants and the key intermediates were performed at the M06-2X-D3/6-311+G(d,p)(SMD, toluene) theoretical level. The gas-phase proton affinity (PA) [66], defined as the enthalpy change (ΔH) of the deprotonation reaction (Equation (1)), was used to evaluate the reactivity of the nitrogen atoms in guanidine (G):
GH+ (g) → G (g) + H+ (g)   ΔH = PA
To gain insights into the factors affecting activation barriers in the reaction process, we performed activation strain model (ASM) [67] (or distortion/interaction model [68]) analysis. Accordingly, the energy barrier (∆E) was decomposed into distortion energy (∆Estrain) and interaction energy (∆Eint) (Equation (2)):
∆E = ∆Estrain + ∆Eint
In addition, the interaction energy (∆Eint) between the strained reactants was further decomposed into electrostatic interactions (∆Velstat), orbital interactions (∆Eoi), and Pauli repulsions (∆EPauli) by energy decomposition analysis (EDA) (Equation (3)) [69]. The EDA and the fragmental orbital interaction analysis were performed with the Amsterdam density functional (ADF) program package [70] at the M06-2X/TZ2P theoretical level.
∆Eint = ∆Velstat + ∆EPauli + ∆Eoi
Atom in molecule (AIM) analysis was carried out using Multiwfn software [71] to reveal the inter- and intramolecular interactions between catalyst and reactant. A positive or negative Laplacian value of the electron density (ρ) at the (3, −1) bond critical point (BCP) indicates that the electron density is divergent or aggregated, respectively [72,73]. Various possible conformations of the protonated guanidine species were generated by Material studio software and optimized with Gaussian 09 program. Two low-energy conformers were studied in the catalytic reaction.

4. Conclusions

The DFT method was adopted to study the reaction mechanism and the origin of enantioselectivity of the aza-Henry reaction between isatin-derived N-Boc ketimine and nitromethane catalyzed by the guanidine–amide catalyst. The calculations showed that the catalytic reaction occurred via a three-step mechanism. The deprotonation of nitromethane was the rate-determining step (RDS), while the C–C bond formation was the chiral-controlling step. The intramolecular hydrogen bonding formed between the amide skeleton and imine unit of guanidine enhanced the rigidity of catalyst, facilitating the imine and amide moiety to simultaneously interact with CH3NO2 and N-Boc ketimine by hydrogen bonding. The repulsion between the CPh3 group in guanidine and the N-Boc group in ketimine played an important role in controlling the enantioselectivity of the product. An unfavorable steric arrangement at the si-face attack pathway enhancing the Pauli repulsion energy as well as strain energy of the reacting species, leading to a predominant R-configuration product. The new catalysts with cyclopropenimine and sulfonamide unit were designed. The strong basicity of the cyclopropenimine moiety accelerated the activation of CH3NO2 by decreasing the energy barrier in the deprotonation step. The hydrogen bonding from diamine oriented ketimine well. The repulsion between the N-Boc group in ketimine and 2,6-difluoro-benzenesulfonamide and Cy groups in the catalyst raised the energy of the C–C bond formation transition state along the si-face attack pathway, leading to the formation of a predominant R-configuration product.

Supplementary Materials

The following are available online. Table S1: Comparison of key geometric parameters obtained by experiments and theoretical calculations at the M06-2X-D3/6-31G(d,p) (SMD, toluene) level; Figure S1: Contour line maps of Laplace field for four intermediates. The blue points represent BCPs, and the solid and dashed lines represent the areas with positive and negative Laplacian of electron density, respectively; Figure S2: Selected bond critical points with corresponding Laplacian (∇2ρ) and electronic density (ρ) values for four transition states G1-I-re-TS2 ~ G1-II-si-TS2 by AIM analysis; Figure S3: Schematic molecular orbital interaction diagram for transition state G1-I-re-TS2, constructed by G1-R2 (Frag. 1) and N-Boc ketimine (Frag. 2) fragments obtained with the ADF program; Figure S4: Schematic molecular orbital interaction diagram for transition state G1-I-si-TS2, constructed by G1-R2 (Frag.1) and N-Boc ketimine (Frag. 2) fragments obtained with the ADF program; Figure S5: Optimized geometries of transition states G1-I-re-TS2-a ~ G1-II-si-TS2-a. Relative Gibbs free energies are given in kcal·mol−1; Figure S6: Relaxed potential energy scan of guanidine cation, calculated by scanning the dihedral angle N5-C1-N2-Cy (a) and N5-C1-N3-Cy (b) at M06-2X-D3/6-31G(d,p)(SMD, toluene) theoretical level; Figure S7: Noncovalent interaction (NCI) plots near bulky CPh3 group areas for G1-I-re-TS2 ~ G1-II-si-TS2. Strong and attractive interactions are blue, weak interactions are green, and strong and repulsive interactions are red; Figure S8: Energy profiles for aza-Henry reaction between N-COOEt ketimine (R1b) and nitromethane (R2) catalyzed by guanidine (G1) along re-face and si-face pathways in model I; Figure S9: Energy profiles for aza-Henry reaction between N-Boc ketimine (R1a) and nitromethane (R2) catalyzed by guanidine (G2) along re-face and si-face pathways in model I.

Author Contributions

Conceptualization, D.T., C.H. and Z.S.; methodology, J.H. and Z.S.; software, J.H. and Z.S.; validation, D.T., C.H. and Z.S.; formal analysis, J.H. and Z.S. investigation, J.H.; resources, D.T., C.H. and Z.S.; data curation, J.H. and Z.S.; writing—original draft preparation, J.H. and Z.S.; writing—review and editing, J.H., C.H. and Z.S.; project administration, Z.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (No. 21973066), the Fundamental Research Funds for the Central Universities (No. 2019SCUH0005) and the 111 project (B17030).

Data Availability Statement

Data are contained within the article or Supplementary Materials.

Conflicts of Interest

The authors declare no conflict of interest.

Sample Availability

Samples of the compounds are not available from the authors.

References

  1. Marques-Lopez, E.; Merino, P.; Tejero, T.; Herrera, R.P. Catalytic Enantioselective Aza-Henry Reactions. Eur. J. Org. Chem. 2009, 15, 2401–2420. [Google Scholar] [CrossRef]
  2. Nef, J.U. Ueber die Constitution der Salze der Nitroparaffine. Justus Liebigs Ann. Chem. 1894, 280, 263–291. [Google Scholar] [CrossRef]
  3. Ballini, R.; Petrini, M. Recent Synthetic Developments in the Nitro to Carbonyl Conversion (Nef Reaction). Tetrahedron 2004, 60, 1017–1047. [Google Scholar] [CrossRef]
  4. Krawczyk, H.; Albrecht, L.; Wojciechowski, J.; Wolf, W.M. Spontaneous Nef Reaction of 3-Aryl-2-(Diethoxyphosphoryl)-4-Nitroalkanoic Acids. Tetrahedron 2006, 62, 9135–9145. [Google Scholar] [CrossRef]
  5. Bhat, C.; Tilve, S.G. Henry-Nef Reaction: A Practical and Versatile Chiral Pool Route to 2-Substituted Pyrrolidine and Piperidine Alkaloids. Tetrahedron 2013, 69, 6129–6143. [Google Scholar] [CrossRef]
  6. Ju, M.; Guan, W.Y.; Schomaker, J.M.; Harper, K.C. Sequential Reduction of Nitroalkanes Mediated by CS2 and Amidine/Guanidine Bases: A Controllable Nef Reaction. Org. Lett. 2019, 21, 8893–8898. [Google Scholar] [CrossRef]
  7. Lloyd, D.H.; Nichols, D.E. Nickel Boride/Hydrazine Hydrate: Reduction of Aromatic and Aliphatic Nitro Compounds. Synthesis of 4-(Benzyloxy)Indole and α-Alkyltryptamines. J. Org. Chem. 1986, 51, 4294–4295. [Google Scholar] [CrossRef]
  8. Lucet, D.; Gall, T.L.; Mioskowski, C. The Chemistry of Vicinal Diamines. Angew. Chem. Int. Ed. 1998, 37, 2581–2627. [Google Scholar] [CrossRef]
  9. Kotti, S.R.S.S.; Timmons, C.; Li, G.G. Vicinal Diamino Functionalities as Privileged Structural Elements in Biologically Active Compounds and Exploitation of Their Synthetic Chemistry. Chem. Biol. Drug. Des. 2006, 67, 101–114. [Google Scholar] [CrossRef] [PubMed]
  10. Kizirian, J.C. Chiral Tertiary Diamines in Asymmetric Synthesis. Chem. Rev. 2008, 108, 140–205. [Google Scholar] [CrossRef]
  11. Yamada, K.; Moll, G.; Shibasaki, M. The First Enantioselective and Diastereoselective Catalytic Nitro-Mannich Reaction: A New Entry to Chiral Vicinal Diamines. Synlett 2001, SI, 980–982. [Google Scholar] [CrossRef] [Green Version]
  12. Palomo, C.; Oiarbide, M.; Halder, R.; Laso, A.; Lópze, R. Enantioselective Aza-Henry Reactions Assisted by Zn(II) and N-Methylephedrine. Angew. Chem. Int. Ed. 2006, 45, 117–120. [Google Scholar] [CrossRef] [PubMed]
  13. Dudek, A.; Mlynarski, J. Iron-Catalyzed Asymmetric Nitro-Mannich Reaction. J. Org. Chem. 2017, 82, 11218–11224. [Google Scholar] [CrossRef] [PubMed]
  14. Yamada, K.; Harwood, S.J.; Gröger, H.; Shibasaki, M. The First Catalytic Asymmetric Nitro Mannich-Type Reaction Promoted by a New Heterobimetallic Complex. Angew. Chem. Int. Ed. 1999, 38, 3504–3506. [Google Scholar] [CrossRef]
  15. Zhang, S.; Li, Y.N.; Xu, Y.G.; Wang, Z.Y. Recent Progress in Copper Catalyzed Asymmetric Henry Reaction. Chin. Chem. Lett. 2018, 29, 873–883. [Google Scholar] [CrossRef]
  16. Okino, T.; Nakamura, S.; Furukawa, T.; Takemoto, Y. Enantioselective Aza-Henry Reaction Catalyzed by a Bifunctional Organocatalyst. Org. Lett. 2004, 6, 625–627. [Google Scholar] [CrossRef] [PubMed]
  17. Ting, A.; Schaus, S.E. Organocatalytic Asymmetric Mannich Reactions: New Methodology, Catalyst Design, and Synthetic Applications. Eur. J. Org. Chem. 2007, 2007, 5797–5815. [Google Scholar] [CrossRef]
  18. Belding, L.; Taimoory, S.M.; Dudding, T. Mirroring Enzymes: The Role of Hydrogen Bonding in an Asymmetric Organocatalyzed Aza-Henry Reaction-a DFT Study. ACS Catal. 2015, 5, 343–349. [Google Scholar] [CrossRef]
  19. Notz, W.; Tanaka, F.; Watanabe, S.-i.; Chowdari, N.S.; Turner, J.M.; Thayumanavan, R.; Barbas, C.F. The Direct Organocatalytic Asymmetric Mannich Reaction: Unmodified Aldehydes as Nucleophiles. J. Org. Chem. 2003, 68, 9624–9634. [Google Scholar] [CrossRef]
  20. Ochi, M.; Kawasaki, K.; Kataoka, H.; Uchio, Y.; Nishi, H. AG-041R, a Gastrin/CCK-B Antagonist, Stimulates Chondrocyte Proliferation and Metabolism in Vitro. Biochem. Biophys. Res. Commun. 2001, 283, 1118–1123. [Google Scholar] [CrossRef]
  21. Lin, H.; Danishefsky, S.J. Gelsemine: A Thought-Provoking Target for Total Synthesis. Angew. Chem. Int. Ed. 2003, 42, 36–51. [Google Scholar] [CrossRef]
  22. Oost, T.; Backfisch, G.; Bhowmik, S.; van Gaalen, M.M.; Geneste, H.; Hornberger, W.; Lubisch, W.; Netz, A.; Unger, L.; Wernet, W. Potent and Selective Oxindole-based Vasopressin 1b Receptor Antagonists with Improved Pharmacokinetic Properties. Bioorg. Med. Chem. Lett. 2011, 21, 3828–3831. [Google Scholar] [CrossRef] [PubMed]
  23. Berlinck, R.G.S.; Romminger, S. The Chemistry and Biology of Guanidine Natural Products. Nat. Prod. Rep. 2016, 33, 456–490. [Google Scholar] [CrossRef] [PubMed]
  24. Arai, T.; Matsumura, E.; Masu, H. Bis(imidazolidine)pyridine-NiCl2 Catalyst for Nitro-Mannich Reaction of Isatin-Derived N-Boc Ketimines: Asymmetric Synthesis of Chiral 3-Substituted 3-Amino-2-oxindoles. Org. Lett. 2014, 16, 2768–2771. [Google Scholar] [CrossRef]
  25. Holmquist, M.; Blay, G.; Pedro, J.R. Highly Enantioselective Aza-Henry Reaction with Isatin N-Boc Ketimines. Chem. Commun. 2014, 50, 9309–9312. [Google Scholar] [CrossRef] [PubMed]
  26. Tan, C.; Liu, X.H.; Wang, L.W.; Wang, J.; Feng, X.M. Highly Enantioselective Aza-Henry Reaction of Ketoimines Catalyzed by Chiral N, N′-Dioxide-Copper(I) Complexes. Org. Lett. 2008, 10, 5305–5308. [Google Scholar] [CrossRef] [PubMed]
  27. Bernardi, L.; Fini, F.; Herrera, R.P.; Ricci, A.; Sgarzani, V. Enantioselective Aza-Henry Reaction Using Cinchona Organocatalysts. Tetrahedron 2006, 62, 375–380. [Google Scholar] [CrossRef]
  28. Bode, C.M.; Ting, A.; Schaus, S.E. A General Organic Catalyst for Asymmetric Addition of Stabilized Nucleophiles to Acyl Imines. Tetrahedron 2006, 62, 11499–11505. [Google Scholar] [CrossRef]
  29. Kumar, A.; Kuar, J.; Chimni, S.S.; Jassal, A.K. Organocatalytic Enantioselective Aza-Henry Reaction of Ketimines Derived from Isatins: Access to Optically Active 3-Amino-2-Oxindoles. RSC Adv. 2014, 4, 24816–24819. [Google Scholar] [CrossRef]
  30. Li, P.; Sun, D.W.; Jiang, M.; Liu, J.T. Asymmetric Aza-Henry Reaction of Fluoromethylated Imines Catalyzed by Cinchona-Derived Bifunctional Thiourea. Tetrahedron 2019, 75, 603–607. [Google Scholar] [CrossRef]
  31. Rampalakos, C.; Wulff, W.D. A Novel Bis-Thiourea Organocatalyst for the Asymmetric Aza-Henry Reaction. Adv. Synth. Catal. 2008, 350, 1785–1790. [Google Scholar] [CrossRef] [PubMed]
  32. Hajra, S.; Jana, B. Quinine-Based Trifunctional Organocatalyst for Tandem Aza-Henry Reaction-Cyclization: Asymmetric Synthesis of Spiroxindole-Pyrrolidine/Piperidines. Org. Lett. 2017, 19, 4778–4781. [Google Scholar] [CrossRef] [PubMed]
  33. Nunez, M.G.; Farley, A.J.; Dixon, D.J. Bifunctional Iminophosphorane Organocatalysts for Enantioselective Synthesis: Application to the Ketimine Nitro-Mannich Reaction. J. Am. Chem. Soc. 2013, 135, 16348–16351. [Google Scholar] [CrossRef]
  34. Xue, Y.S.; Wang, Y.H.; Cao, Z.Y.; Zhou, J.; Chen, Z.X. Computational Insight into the Cooperative Role of Non-covalent Interactions in the Aza-Henry Reaction Catalyzed by Quinine Derivatives: Mechanism and Enantioselectivity. Org. Biomol. Chem. 2016, 14, 9588–9597. [Google Scholar] [CrossRef] [PubMed]
  35. Wang, J.D.; Liu, Y.; Liu, Y.X.; Wei, Z.L.; Cao, J.G.; Liang, D.P.; Lin, Y.J.; Duan, H.F. L-tert-Leucine Derived Urea-Ammonium Salts: Efficient Bifunctional Phase Transfer Catalysts for Highly Diastereo- and Enantioselective Aza-Henry Reaction of Isatin-derived N-Boc Ketimines with α-Aryl Nitromethanes. Tetrahedron 2019, 75, 2883–2892. [Google Scholar] [CrossRef]
  36. Sohtome, Y.; Nagasawa, K. Dynamic Asymmetric Organocatalysis: Cooperative Effects of Weak Interactions and Conformational Flexibility in Asymmetric Organocatalysts. Chem. Commun. 2012, 48, 7777–7789. [Google Scholar] [CrossRef] [PubMed]
  37. Fu, X.; Loh, W.T.; Zhang, Y.; Chen, T.; Ma, T.; Liu, H.; Wang, J.; Tan, C.H. Chiral Guanidinium Salt Catalyzed Enantioselective Phospha-Mannich Reactions. Angew. Chem. Int. Ed. 2009, 48, 7387–7390. [Google Scholar] [CrossRef]
  38. Corey, E.J.; Grogan, M.J. Enantioselective Synthesis of α-Amino Nitriles from N-Benzhydryl Imines and HCN with a Chiral Bicyclic Guanidine as Catalyst. Org. Lett. 1999, 1, 157–160. [Google Scholar] [CrossRef]
  39. Cho, B.; Wong, M.W. Unconventional Bifunctional Lewis-Brønsted Acid Activation Mode in Bicyclic Guanidine-Catalyzed Conjugate Addition Reactions. Molecules 2015, 20, 15108–15121. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  40. Xue, H.S.; Jiang, D.F.; Jiang, H.; Kee, C.W.; Hirao, H.; Nishimura, T.; Wong, M.W.; Tan, C.H. Mechanistic Insights into Bicyclic Guanidine-Catalyzed Reactions from Microscopic and Macroscopic Perspectives. J. Org. Chem. 2015, 80, 5745–5752. [Google Scholar] [CrossRef]
  41. Li, J.; Jiang, W.Y.; Han, K.L.; He, G.Z.; Li, C. Density Functional Study on the Mechanism of Bicyclic Guanidine-Catalyzed Strecker Reaction. J. Org. Chem. 2003, 68, 8786–8789. [Google Scholar] [CrossRef]
  42. Kee, C.W.; Peh, K.Q.E.; Wong, M.W. Coupling Reactions of Alkynyl Indoles and CO2 by Bicyclic Guanidine: Origin of Catalytic Activity? Chem. Asian J. 2017, 12, 1780–1789. [Google Scholar] [CrossRef] [PubMed]
  43. Cho, B.; Tan, C.H.; Wong, M.W. Sequential Catalytic Role of Bifunctional Bicyclic Guanidine in Asymmetric Phospha-Michael Reaction. Org. Biomol. Chem. 2011, 9, 4550–4557. [Google Scholar] [CrossRef] [Green Version]
  44. Fang, B.; Liu, X.H.; Zhao, J.N.; Tang, Y.; Lin, L.L.; Feng, X.M. Chiral Bifunctional Guanidine-catalyzed Enantioselective Aza-Henry Reaction of Isatin-derived Ketimines. J. Org. Chem. 2015, 80, 3332–3338. [Google Scholar] [CrossRef] [PubMed]
  45. Cao, W.D.; Liu, X.H.; Feng, X.M. Chiral Organobases: Properties and Applications in Asymmetric Catalysis. Chin. Chem. Lett. 2018, 29, 1201–1208. [Google Scholar] [CrossRef]
  46. Dong, S.X.; Feng, X.M.; Liu, X.H. Chiral Guanidines and Their Derivatives in Asymmetric Synthesis. Chem. Soc. Rev. 2018, 47, 8525–8540. [Google Scholar] [CrossRef]
  47. Chou, H.; Leow, D.; Tan, C.H. Recent Advances in Chiral Guanidine-Catalyzed Enantioselective Reactions. Chem. Asian J. 2019, 14, 3803–3822. [Google Scholar] [CrossRef]
  48. Liu, X.H.; Lin, L.L.; Feng, X.M. Amide-based Bifunctional Organocatalysts in Asymmetric Reactions. Chem. Commun. 2009, 41, 6145–6158. [Google Scholar] [CrossRef]
  49. Li, J.; Su, Z.S.; Wang, J.M.; Hu, C.W. Mechanistic Investigations on Asymmetric N-H Insertion of Amines Catalyzed by Palladium-chiral Guanidine Complex. J. Catal. 2018, 364, 426–436. [Google Scholar] [CrossRef]
  50. Li, J.; Meng, X.X.; Hu, C.W.; Su, Z.S. Cooperative Catalysis of Chiral Guanidine and Rh2(OAc)4 in Asymmetric O-H Insertion of Carboxylic Acid: A Theoretical Investigation. J. Org. Chem. 2019, 84, 15020–15031. [Google Scholar] [CrossRef]
  51. Emamian, S.; Lv, T.; Kruse, H.; Emamian, H. Exploring Nature and Predicting Strength of Hydrogen Bonds: A Correlation Analysis between Atoms-in-Molecules Descriptors, Binding Energies, and Energy Components of Symmetry-Adapted Perturbation Theory. J. Comput. Chem. 2019, 40, 2868–2881. [Google Scholar] [CrossRef]
  52. Manzetti, S.; Lv, T. The Geometry and Electronic Structure of Aristolochic Acid: Possible Implications for a Frozen Resonance. J. Phys. Org. Chem. 2013, 26, 473–483. [Google Scholar] [CrossRef]
  53. Schneebeli, S.T.; Hall, M.L.; Breslow, R.; Friesner, R. Quantitative DFT Modeling of the Enantiomeric Excess for Dioxirane-catalyzed Epoxidations. J. Am. Chem. Soc. 2009, 131, 3965–3973. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  54. Fernández, I.; Bickelhaupt, F.M. The Activation Strain Model and Molecular Orbital Theory: Understanding and Designing Chemical Reactions. Chem. Soc. Rev. 2014, 43, 4953–4967. [Google Scholar] [CrossRef]
  55. Bickelhaupt, F.M.; Houk, K.N. Analyzing Reaction Rates with the Distortion/Interaction-Activation Strain Model. Angew. Chem. Int. Ed. 2017, 56, 10070–10086. [Google Scholar] [CrossRef] [Green Version]
  56. Kozuch, S.; Shaik, S. A Combined Kinetic-Quantum Mechanical Model for Assessment of Catalytic Cycles: Application to Cross-Coupling and Heck Reactions. J. Am. Chem. Soc. 2006, 128, 3355–3365. [Google Scholar] [CrossRef] [PubMed]
  57. Bandar, J.S.; Lambert, T.H. Enantioselective Brønsted Base Catalysis with Chiral Cyclopropenimines. J. Am. Chem. Soc. 2012, 134, 5552–5555. [Google Scholar] [CrossRef]
  58. Guest, M.; Sueur, R.L.; Pilkington, M.; Dudding, T. Development of an Unsymmetrical Cyclopropenimine-Guanidine Platform for Accessing Strongly Basic Proton Sponges and Boron-Difluoride Diaminonaphthalene Fluorophores. Chem. Eur. J. 2020, 26, 8608–8620. [Google Scholar] [CrossRef]
  59. Ruan, S.; Lin, X.B.; Xie, L.H.; Lin, L.L.; Feng, X.M.; Liu, X.H. Asymmetric Synthesis of 3-Aminodihydrocoumarins via the Chiral Guanidine Catalyzed Cascade Reaction of Azlactones. Org. Chem. Front. 2018, 5, 32–35. [Google Scholar] [CrossRef]
  60. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
  61. Zhao, Y.; Truhlar, D.G. The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
  62. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  63. Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Eectron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef] [PubMed]
  64. Gonzalez, C.; Schlegel, H.B. An Improved Algorithm for Reaction-path Following. J. Chem. Phys. 1989, 90, 2154–2161. [Google Scholar] [CrossRef]
  65. Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular Interactions from a Natural Bond Orbital, Donor-acceptor Viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
  66. Carlosa, L.R.; Loroa, H.; Lagob, A.F.; Dávalos, J.Z. Gas-phase Proton Afnity and Basicity of Hydroxybenzophenones. Chem. Phys. Lett. 2018, 713, 132–136. [Google Scholar] [CrossRef]
  67. Wolters, L.P.; Bickelhaupt, F.M. The Activation Strain Model and Molecular Orbital Theory. WIREs Comput. Mol. Sci. 2015, 5, 324–343. [Google Scholar] [CrossRef]
  68. Ess, D.H.; Houk, K.N. Distortion/Interaction Energy Control of 1,3-Dipolar Cycloaddition Reactivity. J. Am. Chem. Soc. 2007, 129, 10646–10647. [Google Scholar] [CrossRef]
  69. Hopffgarten, M.V.; Frenking, G. Energy Decomposition Analysis. WIREs Comput. Mol. Sci. 2012, 2, 43–62. [Google Scholar] [CrossRef]
  70. Te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Guerra, C.F.; Gisbergen, S.J.A.V.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
  71. Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
  72. Bader, R.F.W.; Beddall, P.M. Virial Field Relationship for Molecular Charge Distributions and the Spatial Partitioning of Molecular Properties. J. Chem. Phys. 1972, 56, 3320–3329. [Google Scholar] [CrossRef]
  73. Bianchi, R.; Gervasio, G.; Marabello, D. Experimental Electron Density Analysis of Mn2(CO)10: Metal-Metal and Metal-Ligand Bond Characterization. Inorg. Chem. 2000, 39, 2360–2366. [Google Scholar] [CrossRef] [PubMed]
Molecules 26 01965 sch001 550
Scheme 1. Asymmetric aza-Henry reaction of isatin-derived N-protected ketimines (R1) and nitromethane (R2) catalyzed by guanidine–amide catalysts.
Scheme 1. Asymmetric aza-Henry reaction of isatin-derived N-protected ketimines (R1) and nitromethane (R2) catalyzed by guanidine–amide catalysts.
Molecules 26 01965 sch001
Molecules 26 01965 sch002 550
Scheme 2. Mechanism of aza-Henry reaction between ketimine (R1a and R1b) and nitromethane (R2), catalyzed by guanidine–amide catalyst (G1).
Scheme 2. Mechanism of aza-Henry reaction between ketimine (R1a and R1b) and nitromethane (R2), catalyzed by guanidine–amide catalyst (G1).
Molecules 26 01965 sch002
Molecules 26 01965 g001 550
Figure 1. Optimized structures of G1-COM, G1-TS1 and G1-IM1 and their relative Gibbs free energies (in kcal·mol−1). The distances are in Å. Laplacian (∇2ρ) and electronic density (ρ) values of the selected bond critical points (BCP) in G1-COM were obtained by atom in molecule (AIM) analysis.
Figure 1. Optimized structures of G1-COM, G1-TS1 and G1-IM1 and their relative Gibbs free energies (in kcal·mol−1). The distances are in Å. Laplacian (∇2ρ) and electronic density (ρ) values of the selected bond critical points (BCP) in G1-COM were obtained by atom in molecule (AIM) analysis.
Molecules 26 01965 g001
Molecules 26 01965 sch003 550
Scheme 3. Four possible reaction pathways along re- or si-face attacks to obtain the R- or S-configuration products, respectively.
Scheme 3. Four possible reaction pathways along re- or si-face attacks to obtain the R- or S-configuration products, respectively.
Molecules 26 01965 sch003
Molecules 26 01965 g002 550
Figure 2. (a) The natural atom charges at H atoms in guanidine cation species, obtained by natural bond orbital (NBO) analysis. (b) Electrostatic potential (ESP) mapped Van der Waals surface of protonated G1. The redder the color, the more positive the ESP. The purple and red spheres represented the local minima and maxima points, respectively.
Figure 2. (a) The natural atom charges at H atoms in guanidine cation species, obtained by natural bond orbital (NBO) analysis. (b) Electrostatic potential (ESP) mapped Van der Waals surface of protonated G1. The redder the color, the more positive the ESP. The purple and red spheres represented the local minima and maxima points, respectively.
Molecules 26 01965 g002
Molecules 26 01965 g003 550
Figure 3. Energy profiles for aza-Henry reaction between N-Boc ketimine (R1a) and nitromethane (R2) catalyzed by guanidine (G1) along re- and si-face pathways in models I and II, respectively.
Figure 3. Energy profiles for aza-Henry reaction between N-Boc ketimine (R1a) and nitromethane (R2) catalyzed by guanidine (G1) along re- and si-face pathways in models I and II, respectively.
Molecules 26 01965 g003
Molecules 26 01965 g004 550
Figure 4. Optimized geometries of four transition states along re- or si-face attack pathways. The relative Gibbs free energies are given in kcal·mol−1.
Figure 4. Optimized geometries of four transition states along re- or si-face attack pathways. The relative Gibbs free energies are given in kcal·mol−1.
Molecules 26 01965 g004
Molecules 26 01965 g005 550
Figure 5. (a) ASM analysis of aza-Henry reaction between N-Boc ketimine (R1a) and nitromethane (R2) along the reaction coordinate projected onto the C13⋯C15 distance for re- and si-pathways. (b) Evolution of ∆Eint of two energy components along the reaction coordinate.
Figure 5. (a) ASM analysis of aza-Henry reaction between N-Boc ketimine (R1a) and nitromethane (R2) along the reaction coordinate projected onto the C13⋯C15 distance for re- and si-pathways. (b) Evolution of ∆Eint of two energy components along the reaction coordinate.
Molecules 26 01965 g005
Molecules 26 01965 g006 550
Figure 6. Optimized structures and the relative Gibbs free energy (kcal·mol−1) of transition states G1-1b-I-re-TS2 and G1-1b-I-si-TS2 in the C–C bond formation step in the aza-Henry reaction between ketimine (R1b) and nitromethane (R2) catalyzed by guanidine G1.
Figure 6. Optimized structures and the relative Gibbs free energy (kcal·mol−1) of transition states G1-1b-I-re-TS2 and G1-1b-I-si-TS2 in the C–C bond formation step in the aza-Henry reaction between ketimine (R1b) and nitromethane (R2) catalyzed by guanidine G1.
Molecules 26 01965 g006
Molecules 26 01965 g007 550
Figure 7. Optimized structures of transition states and the relative Gibbs free energies (kcal·mol−1) in the aza-Henry reaction between N-Boc ketimine (R1a) and nitromethane (R2) catalyzed by guanidine G2.
Figure 7. Optimized structures of transition states and the relative Gibbs free energies (kcal·mol−1) in the aza-Henry reaction between N-Boc ketimine (R1a) and nitromethane (R2) catalyzed by guanidine G2.
Molecules 26 01965 g007
Molecules 26 01965 g008 550
Figure 8. Origin of enantioselectivity in the aza-Henry reaction.
Figure 8. Origin of enantioselectivity in the aza-Henry reaction.
Molecules 26 01965 g008
Molecules 26 01965 sch004 550
Scheme 4. New catalysts G3 and G4.
Scheme 4. New catalysts G3 and G4.
Molecules 26 01965 sch004
Molecules 26 01965 g009 550
Figure 9. Optimized geometries of catalysts G3 and G4. The distances are in Å. The H atoms in phenyl and cyclohexyl groups are omitted for clarity.
Figure 9. Optimized geometries of catalysts G3 and G4. The distances are in Å. The H atoms in phenyl and cyclohexyl groups are omitted for clarity.
Molecules 26 01965 g009
Molecules 26 01965 g010 550
Figure 10. Optimized structures and the relative Gibbs free energies (in kcal·mol−1) of two competing transition states (G3-re-TS2 and G3-si-TS2) in the C–C bonding formation step of the aza-Henry reaction catalyzed by G3. The distances are in Å.
Figure 10. Optimized structures and the relative Gibbs free energies (in kcal·mol−1) of two competing transition states (G3-re-TS2 and G3-si-TS2) in the C–C bonding formation step of the aza-Henry reaction catalyzed by G3. The distances are in Å.
Molecules 26 01965 g010
Molecules 26 01965 g011 550
Figure 11. Optimized structures and the relative Gibbs free energies (in kcal·mol−1) of two competing transition states (G4-re-TS2 and G4-si-TS2) in the C–C bonding formation step of the aza-Henry reaction catalyzed by G4. The distances are in Å.
Figure 11. Optimized structures and the relative Gibbs free energies (in kcal·mol−1) of two competing transition states (G4-re-TS2 and G4-si-TS2) in the C–C bonding formation step of the aza-Henry reaction catalyzed by G4. The distances are in Å.
Molecules 26 01965 g011
Molecules 26 01965 g012 550
Figure 12. Energy profiles for aza-Henry reaction between N-Boc ketimine (R1a) and nitromethane (R2) catalyzed by G4 along re-face and si-face pathways, respectively.
Figure 12. Energy profiles for aza-Henry reaction between N-Boc ketimine (R1a) and nitromethane (R2) catalyzed by G4 along re-face and si-face pathways, respectively.
Molecules 26 01965 g012
Molecules 26 01965 sch005 550
Scheme 5. A possible synthesis route of catalyst G4.
Scheme 5. A possible synthesis route of catalyst G4.
Molecules 26 01965 sch005
Table
Table 1. Turnover frequency (TOF) of the catalytic cycle of aza-Henry reactions of isatin-derived ketimine (R1a) and nitromethane (R2) along four pathways. TDI and TDTS are the TOF-determining intermediates and TOF-determining transition states, respectively.
Table 1. Turnover frequency (TOF) of the catalytic cycle of aza-Henry reactions of isatin-derived ketimine (R1a) and nitromethane (R2) along four pathways. TDI and TDTS are the TOF-determining intermediates and TOF-determining transition states, respectively.
PathTDITDTSTOF (s−1)Product
I-reG1-1a-I-re-IM2G1-1a-I-re-TS22.06 × 1010P-R (major)
I-siG1-1a-I-si-IM2G1-1a-I-si-TS22.98 × 108P-S
II-reG1-1a-II-re-IM2G1-1a-II-re-TS21.24 × 1010P-R
II-siG1-1a-II-si-IM2G1-1a-II-si-TS21.03 × 1010P-S
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

He, J.; Tang, D.; Hu, C.; Su, Z. Guanidine–Amide-Catalyzed Aza-Henry Reaction of Isatin-Derived Ketimines: Origin of Selectivity and New Catalyst Design. Molecules 2021, 26, 1965. https://doi.org/10.3390/molecules26071965

AMA Style

He J, Tang D, Hu C, Su Z. Guanidine–Amide-Catalyzed Aza-Henry Reaction of Isatin-Derived Ketimines: Origin of Selectivity and New Catalyst Design. Molecules. 2021; 26(7):1965. https://doi.org/10.3390/molecules26071965

Chicago/Turabian Style

He, Jiajia, Dianyong Tang, Changwei Hu, and Zhishan Su. 2021. "Guanidine–Amide-Catalyzed Aza-Henry Reaction of Isatin-Derived Ketimines: Origin of Selectivity and New Catalyst Design" Molecules 26, no. 7: 1965. https://doi.org/10.3390/molecules26071965

APA Style

He, J., Tang, D., Hu, C., & Su, Z. (2021). Guanidine–Amide-Catalyzed Aza-Henry Reaction of Isatin-Derived Ketimines: Origin of Selectivity and New Catalyst Design. Molecules, 26(7), 1965. https://doi.org/10.3390/molecules26071965

Article Metrics

Back to TopTop